简单单锚系泊系统浮标游动区域探讨

何 静

(重庆工商大学 融智学院,重庆 400055)

【理论研究】

简单单锚系泊系统浮标游动区域探讨

何 静

(重庆工商大学 融智学院,重庆 400055)

单锚系泊系统是海洋观测,海洋运输等领域重要的定位观测方法。本文主要在静力学平衡分析的基础上,建立了带约束条件的目标规划模型,并利用LINGO寻找浮标游动区域半径的最优解。

近海风力;浮力;游动区域;规划模型

近浅海观测网的传输节点由多个单锚系泊系统构成,而每个单锚系泊系统又分为浮标、锚链和锚三部分。假设系泊系统内各部件均为钢材质,且海床平坦、海水密度恒定。在已知该系泊系统布放的海水深度、各部件质量的前提下分析浮标的游动区域,是为了合理设计观测网的需要。明确了浮标的游动范围,就可以确定该片区域放置单锚系泊系统的数量。

一、各部件的受力分析

假设海水静止,不考虑水流力。参照物理意义上的“向上为正,向下为负”的原则,以锚为坐标系原点,在水平面作x轴,经过物体几何中心向上作y轴[1]见(图1),进行二维静力学受力分析。

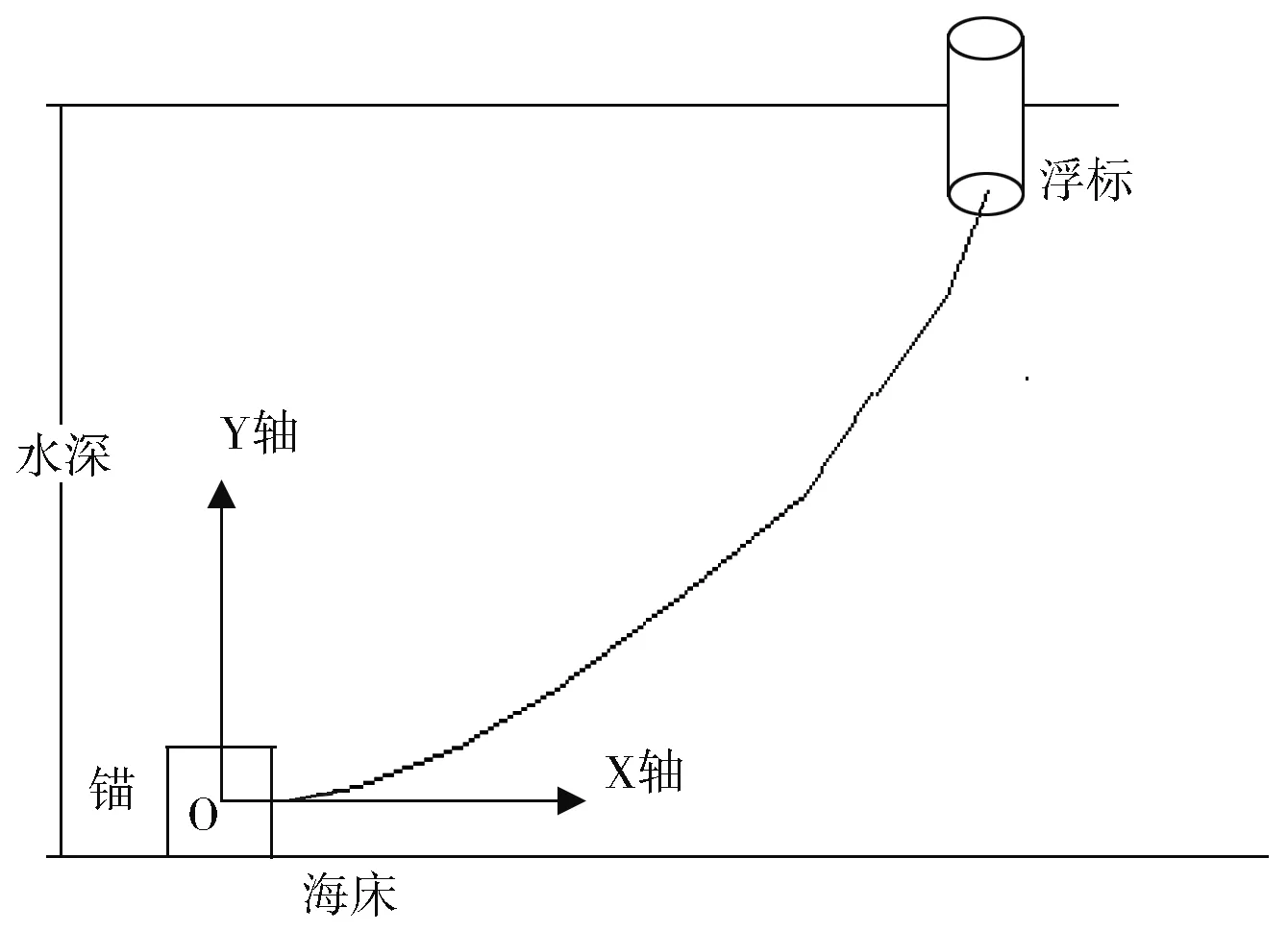
图1

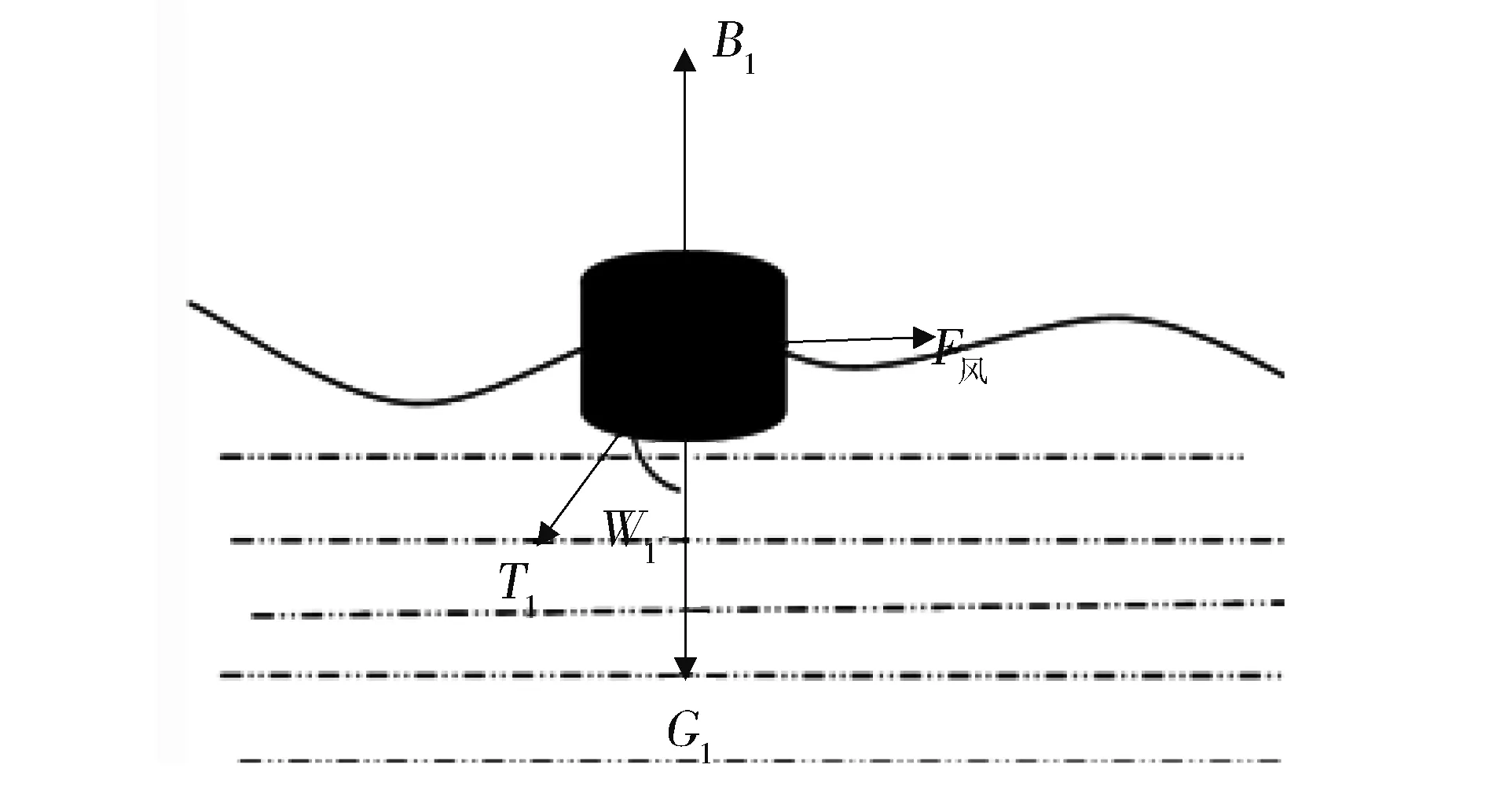
图2

(一)浮标受力分析

设定风向为水平向右,即沿x轴正方向。此时浮标受到的力有:重力G1、浮力B1、风力Fa、锚链张力T1,见(图2)。若浮标重量为m1,浮标的底面积s1,浮标吃水深度为h, 浮标在风向法平面的投影面积s2。由此可根据浮标受力平衡,建立浮标的水平和竖直方向的静力平衡方程。

水平:F风=0.625s2v2=T1sinw1

竖直:ρ=ghs1=m1g+T1cosw1

(二)锚链的受力分析

假设锚链共有n节,则对第F'节锚链进行受力分析,由(图3)所示,它受到的力有重力G2、浮力B2、锚链的向上的张力Ti、向下的张力Ti+1。若任意一节锚链的重量为m2,锚链的体积为Vg。当锚链处于平衡状态时,有如下静态平衡方程:

竖直:ρsgVs+Ticoswi=m2g+Ti+1coswi+1

水平:Tisinwi+Ti+1sinwi+1(i=1,2,…,n)

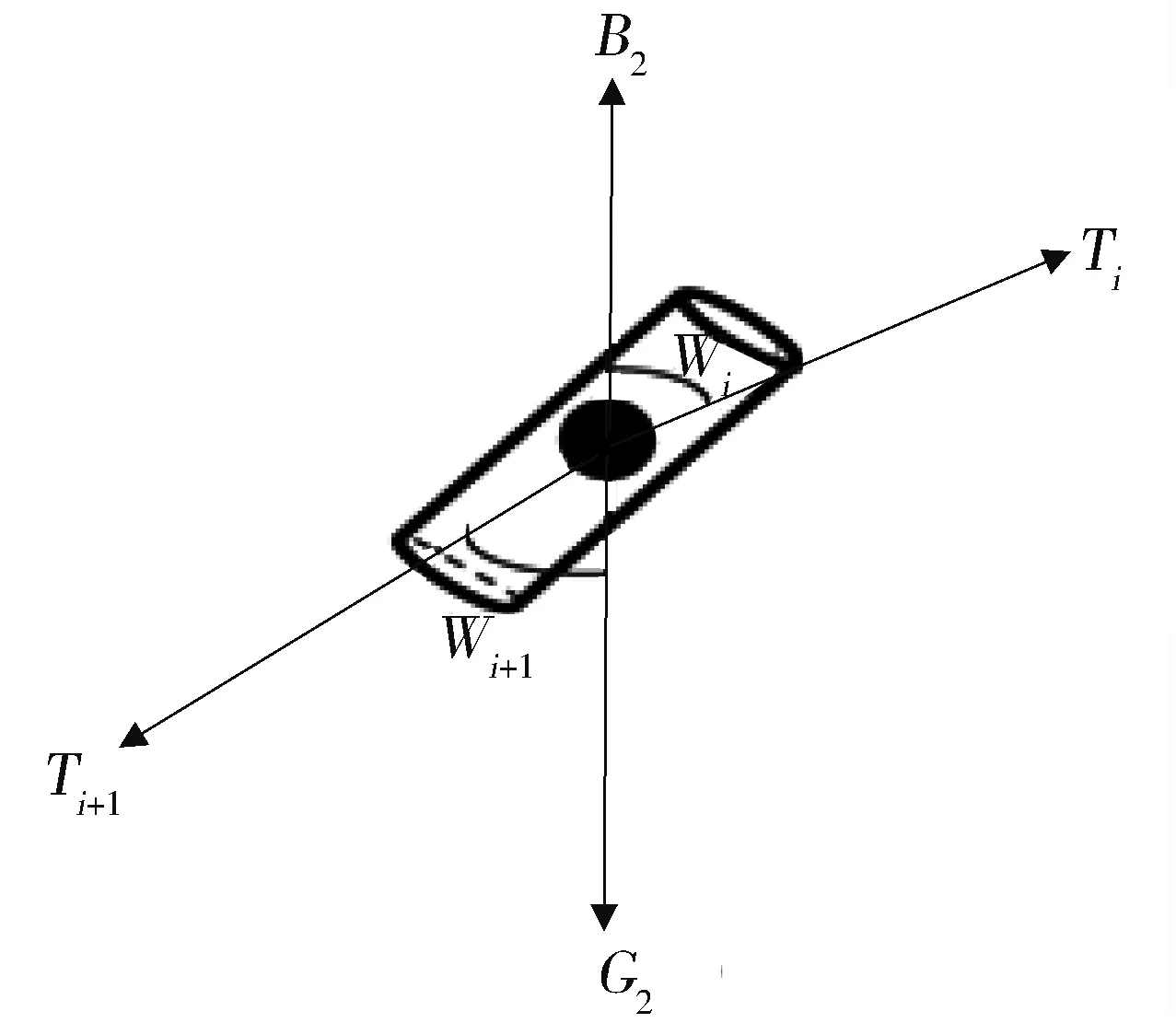
图3

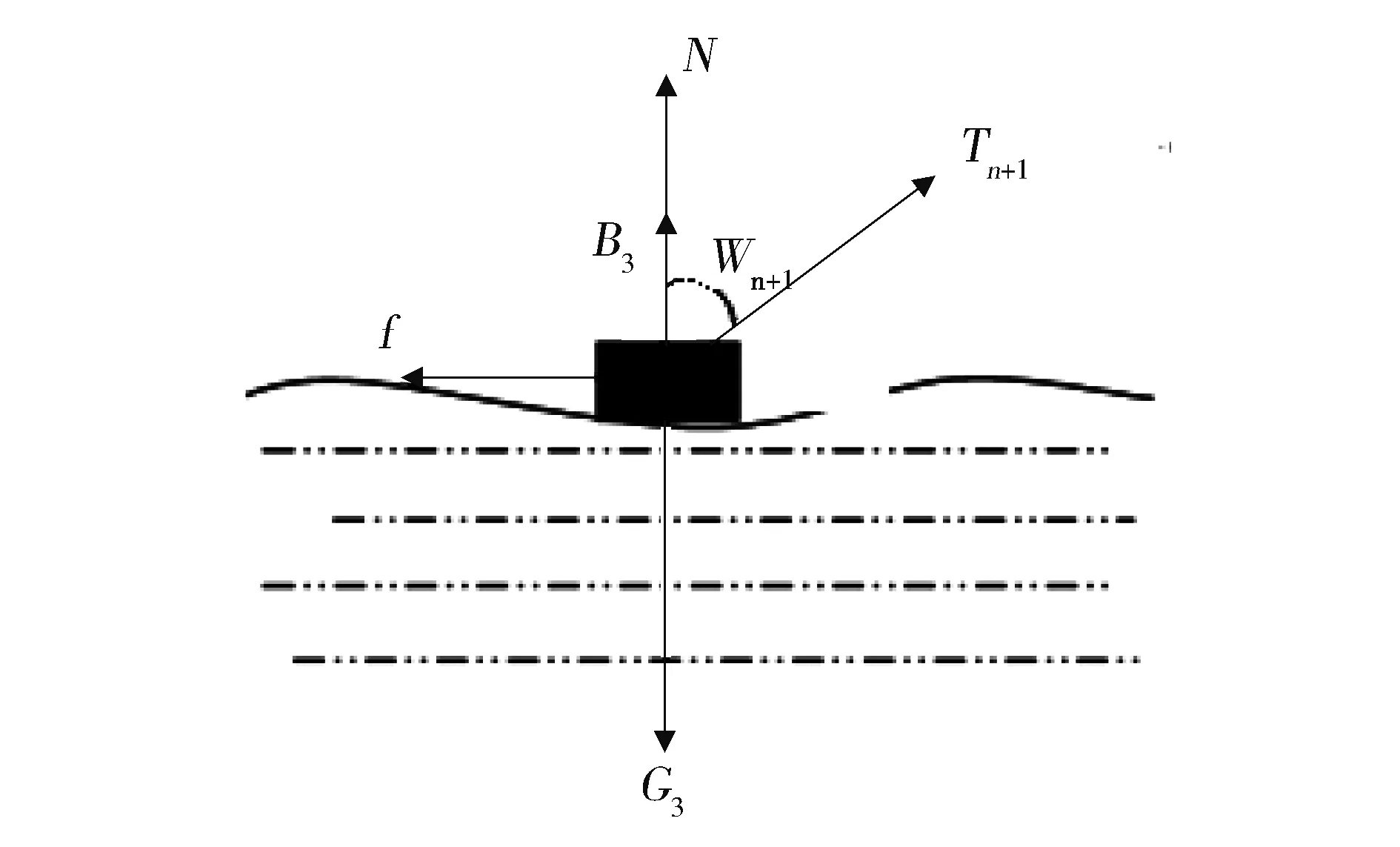
图4

(三)锚的受力分析

由于锚靠自身与海底的摩擦力来阻止走锚现象的发生,对锚进行受力分析见(图4)。锚所受到的力有:锚的重力G3,锚的浮力B3,海底对锚的支撑力N,第n节锚链对锚的张力Tn+1,海底对锚的摩擦力f。

在锚链及各部件强度允许的情况下,附带锚抓的系泊系统可以承受更大的环境载荷。由锚的质量可知f=km3g,其中k为锚所受抓力的特定系数[2-3],且对于小型锚2.5≤k≤6。

要锚不移动只需对水平方向受力建立静态平衡方程如下:

Tn+1·sinwn+1≤km3g

若上式不成立,说明系统将会发生走锚现象。

二、浮标游动区域的确定

当浮标、锚链和锚成一直线时,由静力学分析可知在风力的作用下系泊系统不能平衡,此时浮标会向外游动。在一定的风速条件下,浮标的游动区域应为类环形,所以需要求出近似情况下环的内、外半径。

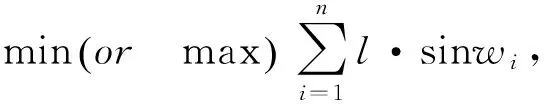
综上可知,根据所建立的带约束条件的目标规划模型,并考虑海水深度限制以及在实际情况下wi的关系,利用Lingo编程即可得出浮标游动的具体区域。

三、实例分析

对图1所示的简单单锚系泊系统布放在近浅海弯水深为20米的平坦海床上,若不考虑海流力及波浪力对系统受力的影响,在海水密度为1.025×103kg/m3,海面风速为20m/s的海域,对单锚系泊系统浮标游动的区域进行分析。该系泊系统主要组成部分为:1个质量为1000kg的圆柱体形浮标,其底面直径和高均为2m,长度为25m共200节的锚链,其中每节锚链质量为875g,1个质量为1500kg的长方体形锚。采用上述经过静力学受力分析得出的带约束条件规划模型,编程计算得出浮标在内、外半径处单锚系泊系统锚链的形态,见图5与与图6。浮标将在半径为(16.6,17.5)的环状区域内游动。

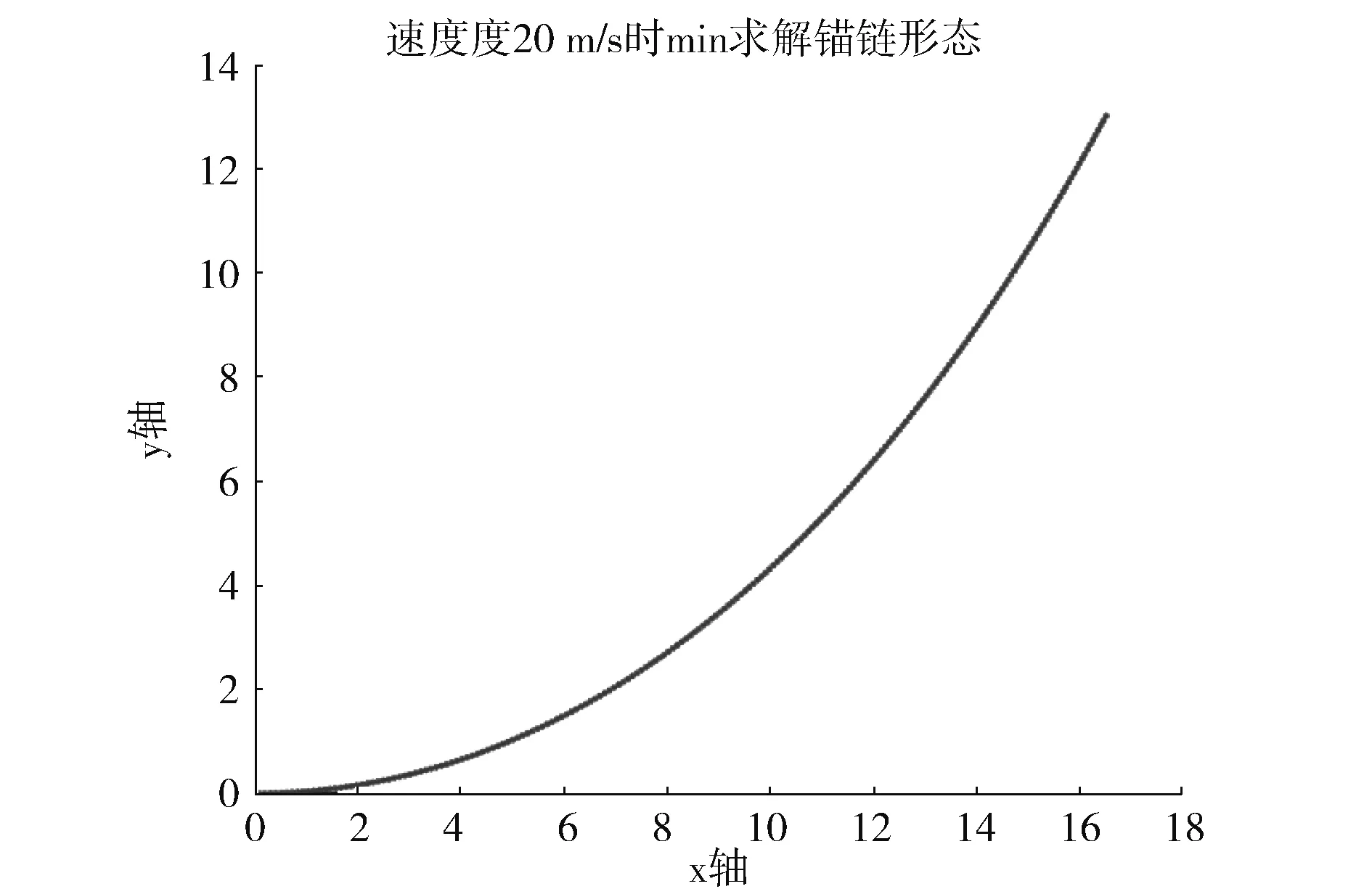
图5

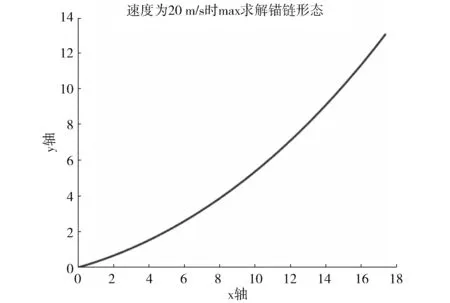
图6

对于单点系泊系统,已有研究多采用迭代计算模型或动力学模型,比较复杂。而本文采用的规划模型,Lingo软件编程实施,能在较短时间内在全局范围下寻找出局部最优解,方便快捷。

[1]王磊.单点系泊系统的动力学研究[D].青岛：中国海洋大学,2012.

[2]李宇服,周俊,陈琦,等.钦州港锚地规划及抓力研究[J].中国水运,2009,9(9):11-13.

[3]王亚洲.深海单点系泊海洋浮标锚泊系统研究[D].青岛：中国海洋大学,2013.

2017-07-05

何静(1982-),女,重庆人，重庆工商大学融智学院讲师,硕士,研究方向:组合优化,教育教改。

G642.0

A

1672-2086(2017)03-0069-02