基于分层分压结构的新型潜水器耐压壳结构设计1)

张 吟 刘小明 雷现奇 孙成奇 方 新 魏宇杰

*(中国科学院力学研究所非线性力学国家重点实验室，北京100190)

†(中国科学院大学工程科学学院，北京100049)

基于分层分压结构的新型潜水器耐压壳结构设计1)

张 吟*,†,2)刘小明*,†雷现奇*,†孙成奇*方 新*魏宇杰*,†

*(中国科学院力学研究所非线性力学国家重点实验室，北京100190)

†(中国科学院大学工程科学学院，北京100049)

耐压壳是深海潜水器中最关键的结构，直接关系到潜水器安全性和总体性能.本文对当今的单层耐压壳结构设计进行了评述，并设计了一种基于分层/分压的新型耐压壳结构，该结构借鉴了自然界的两种深潜动物的结构：抹香鲸分层结构和鹦鹉螺隔片分割螺壳亚结构.综合了这两种结构特性的双层壳结构能够有效提高抗压能力，从而提升深潜能力.与以往单层球壳的耐压壳结构相比，该结构不仅提高了强度，也提高了抗屈曲能力.同时，该结构还兼具大容积、高可靠性、以及避免超厚壳制备上的难点等特征，使得深海潜水器的综合性能得到显著提高.新结构中的桁架将圆壳分割为若干个柱壳亚结构，本文针对此亚结构严格推导了桁架增强壳体抗屈曲的公式.从实验数据中总结出来的泰勒水池公式是目前广泛使用的潜水器壳体设计依据，新推导的公式与之相比只有6%的差别，这使得新型结构设计有了更坚实的理论基础.

耐压壳，深潜器，结构，强度，屈曲

引言

迄今为止,人类研究的海洋区域不足其总面积的10%，以至于尚不能精确绘制出一幅全景式海底地图[1].由于深海中蕴藏巨大的生物、矿产、石油、天然气和可燃冰等资源，美、俄和日等海洋强国一直以来为确保其基于海洋资源开发利用而形成的巨大经济利益，都在大力推进深海探测的研究，其中各国对新型深海载人和无人潜水器的研制和应用最为重视.近年来，我国也加大了深海探测的研发力度，但与航空航天科技的发展速度相比，我国海洋研究的进展是相对缓慢的.制约海洋研究进展速度的一个主要瓶颈因素就是深海潜水器的研制.受限于材料与工程科学的发展，世界各国现在仍然无法制造能长期承受数百乃至上千大气压的载人深海探测设备.而载人深海潜水器核心部件耐压壳的设计成为成败关键所在.

耐压壳，顾名思义，就是要承受海水巨大压力的外层结构.深海潜水器耐压壳结构的设计最早可追溯到1928—1929年间由美国工程师奥梯斯·巴顿(Otis Barton)设计的“深球”号 (Bathysphere)深海潜水器[2].“深球”号于1930—1934年间由巴顿和博物学家威廉·比伯(William Beebe)共同驾驶在百慕大群岛附近海域进行了一系列深潜，于1934年8月15日创造了深度1023m的潜水记录，帮助海洋生物学家实现了在栖息地对深海生物进行直接观测[2].早期另一个重要的深海潜水器耐压壳结构是瑞士人奥古斯特·皮卡德(Auguste Piccard)设计的“深船”号(Bathyscaphe)深海潜水器[3].“深船”号于1948年11月3日下水，下潜深度达到了1370m.“深球”号和“深船”号的成功研发开启了人类向深海探索的一个崭新纪元.至今世界主要国家的深潜器耐压壳结构均采用“深球”号和“深船”号的单层球壳的结构设计.表1是各国设计的深潜器耐压壳结构关键参数.

表1 各国深潜器耐压壳结构关键参数Table 1 The key parameters of the pressure hulls of deep-sea submersibles designed by various countries

目前下潜最深的深潜器为美国的“深海挑战者”号(Deepsea Challenger).在深度10908m的马里亚纳海沟，球壳外壁承受的海水压力约为110MPa，球壳结构不同地方承受的应力远远超过110MPa.以深海挑战者球壳为例，内径1.1m，壳厚66mm在外压110MPa，内压0.1MPa的环境下，球壳的环向应力最大值在球壳内壁，用压力容器的公式可以算出该最大值在1000MPa左右[4]；深海挑战者球壳选用的材料是高强钢，其屈服应力为1400MPa，所以该结构的安全系数为1.4.从表1可以看出，当前可选择的耐压壳材料只有高强度钢和钛合金两种材料，限于材料科学的发展水平，现在并没有可替代这两种合金的材料.

基于现有材料，在材料性能达到极限的情况下，各国的深海潜水器耐压壳结构设计的安全系数依然很低.若耐压壳设计仅从材料角度进行发掘，则必然再次降低安全系数，以至于深潜器整体安全性难以保障.更为合理的是从结构设计的角度，以增加壳体的厚度来降低应力，这实际上也是深海挑战者球壳设计的主要思路.但增加壳体的厚度会大大增加整个深潜器的重量.从表1可以看到，深海挑战者球壳的密度已经远远超过海水的密度了，这样深潜器本身是没法上浮的.这对耐压浮力材料的研制提出了要求[5].作为球壳结构，耐压壳还可能在应力远远没有达到屈服应力之前就发生屈曲失稳.虽然在后屈曲状态，耐压壳还能承受一定的压力，但一旦屈曲失稳，球壳结构局部区域会出现较大应变，导致塑性变形发生，使得球壳总体承受压力的能力急剧降低.球壳结构屈曲的一个重要特性就是对初始缺陷非常敏感，初始缺陷使得球壳结构屈曲的临界压力急剧降低[6-11].除了屈曲失稳，球壳还有突跳失稳；某些情况下，发生突跳失稳的压力甚至还远远低于屈曲压力[8].从制造的角度上讲，要提高球壳的屈曲的应力就要求非常高的加工精度.球壳加工精度的一个重要指标就是真球度，即实测的曲率半径和标准曲率半径的比.以日本“深海6500”号深潜器和俄罗斯“和平2号”深潜器为例，真球度已经非常高了，分别为[10]1.004和1.003.当前单层球壳的耐压仓结构的设计已经把材料性能和加工精度用到极致了，留给材料性能和加工精度的冗余空间是非常小的.

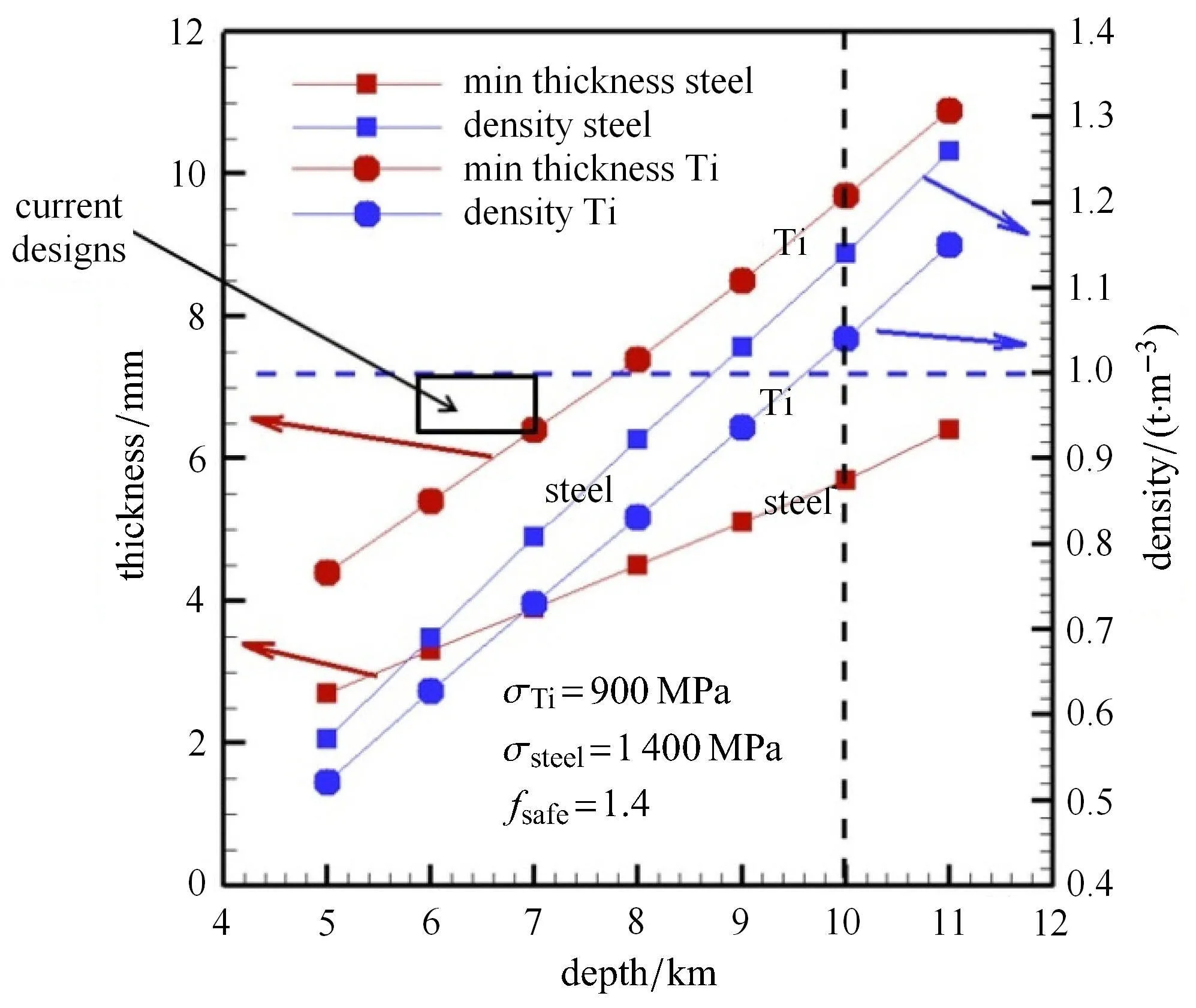
图1 深潜器耐压舱设计最小厚度与密度随设计潜深变化关系Fig.1 The minimum thickness and density of the pressure hull as the functions of the submerging depth

图1显示了钛合金(屈服强度900MPa，安全系数1.4)深潜器的单层壳体所需要的最小厚度以及结构密度与下潜深度的关系.图中方块区域为国内外主要深潜器的壳壁厚度和潜水深度范围.可以看出，随着潜水深度的增加，所需要壳体的最小厚度增加;但是同时，结构密度也在增加，在万米深度以下，结构的密度将会超出1t/m3很多，使得海水浮力不足以支撑整体结构的上浮.这又将会对深潜器浮力材料的设计提出新要求.

此外，传统单层壳体结构的设计，对材料的要求比较高.对于图2所示的单层壳体结构的受力模式，深潜器的主要受力状态是深海中的高压应力，在深潜器的实际工作中，壳体内部压力Pin为0.1MPa(即1个大气压)，壳体外部压力Pout取决于下潜深度.根据模型的受力状态，壳体中径向的应力σr和环向的应力σt为[4]

其中R为球壳内径，t为壳厚度.计算得到的Mises应力按照壳体厚度分布的示意图见图2.最大应力分布于壳体的内表面，其他部分的材料远没有达到屈服.这种单层壳体的设计，使得结构中只有很小部分的材料承受了大应力，大部分材料只承担小应力，这样的设计势必造成材料的浪费.因此，改进结构设计是目前唯一可大幅提高结构耐压性的途径.

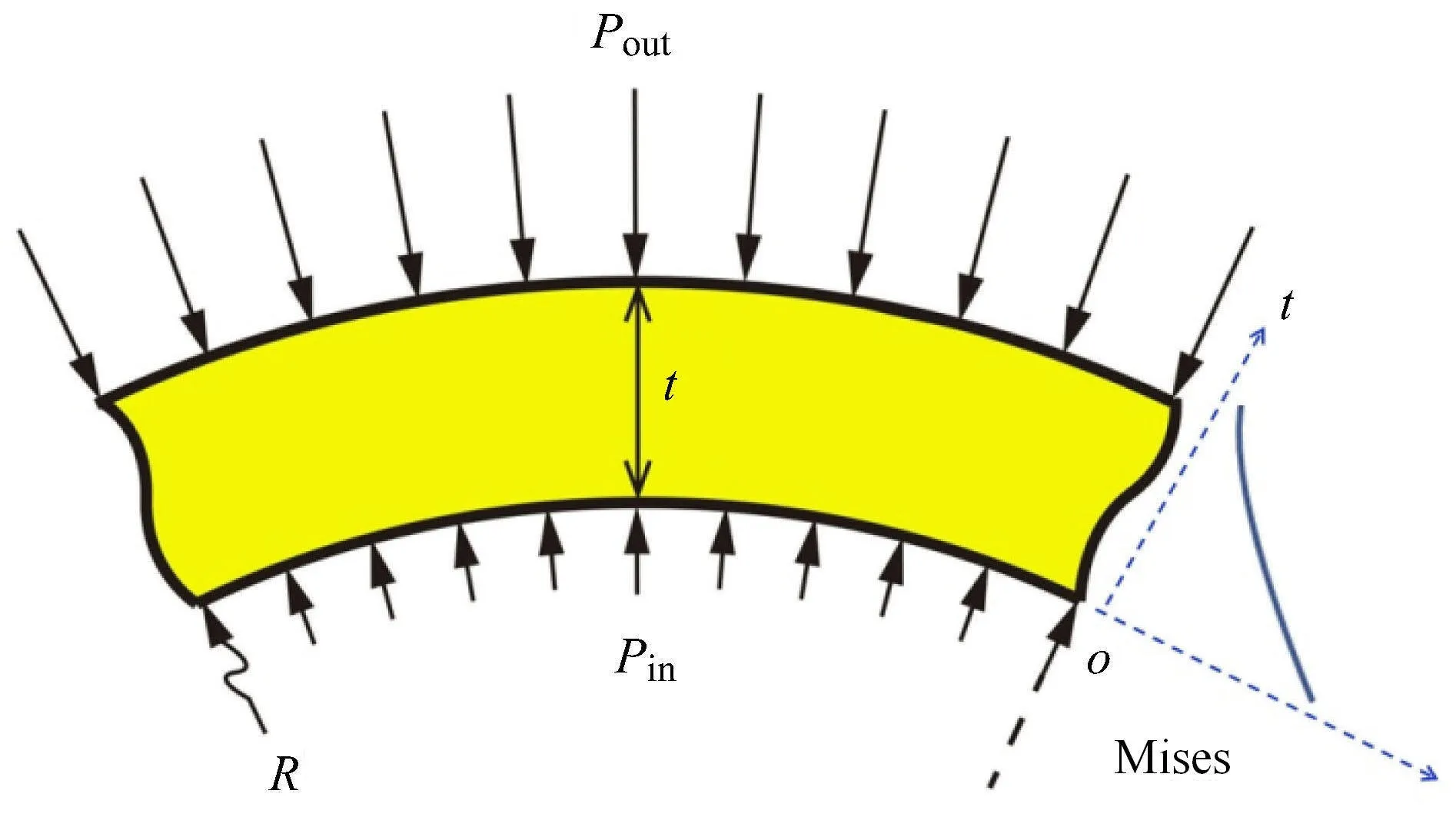
图2 单层壳体的力学模型Fig.2 The free body diagram of one-layer shell

本文设计一种分层的球壳结构，层间采用液压油提供可调控的压力，这样球壳外壁的海水压力就被分散到两层或者多层壳上.分层结构能调控层间液压，优化层间的压力分布.压力分布优化的目标是在满足大容积的前提下，降低壳体内的等效(最大)应力,使得整体密度尽量小.层和层之间则通过桁架连接起来.这样做的好处是：(1)内层壳与外层壳通过桁架固定，不会相对旋转;(2)桁架连接两层壳，使得两层壳成为一个整体,能改变单层壳的高谐波屈曲模态[8]，大幅提高两层壳的抗屈曲和抗突跳能力.本文的理论分析和数值模拟将显示,在承受同样海水压力的情况下，与单层球壳相比，双层球壳的结构应力和密度都有较大幅度的降低，抗屈曲能力显著提高.这为将来的深潜器耐压壳的设计提供了一个新思路.

1 双层耐压壳总体结构和应力分析

图3为双层耐压壳总体结构的示意图.结构分为内外两层，由密排的桁架相连；两层壳体密封之后，层间充满液压油，外部的海水和液压油通过一个可调压的压力平衡器连接(该压力平衡器未出现在图3中);上下两个双层球壳通过法兰盘加固连接.该结构的力学模型见图4.

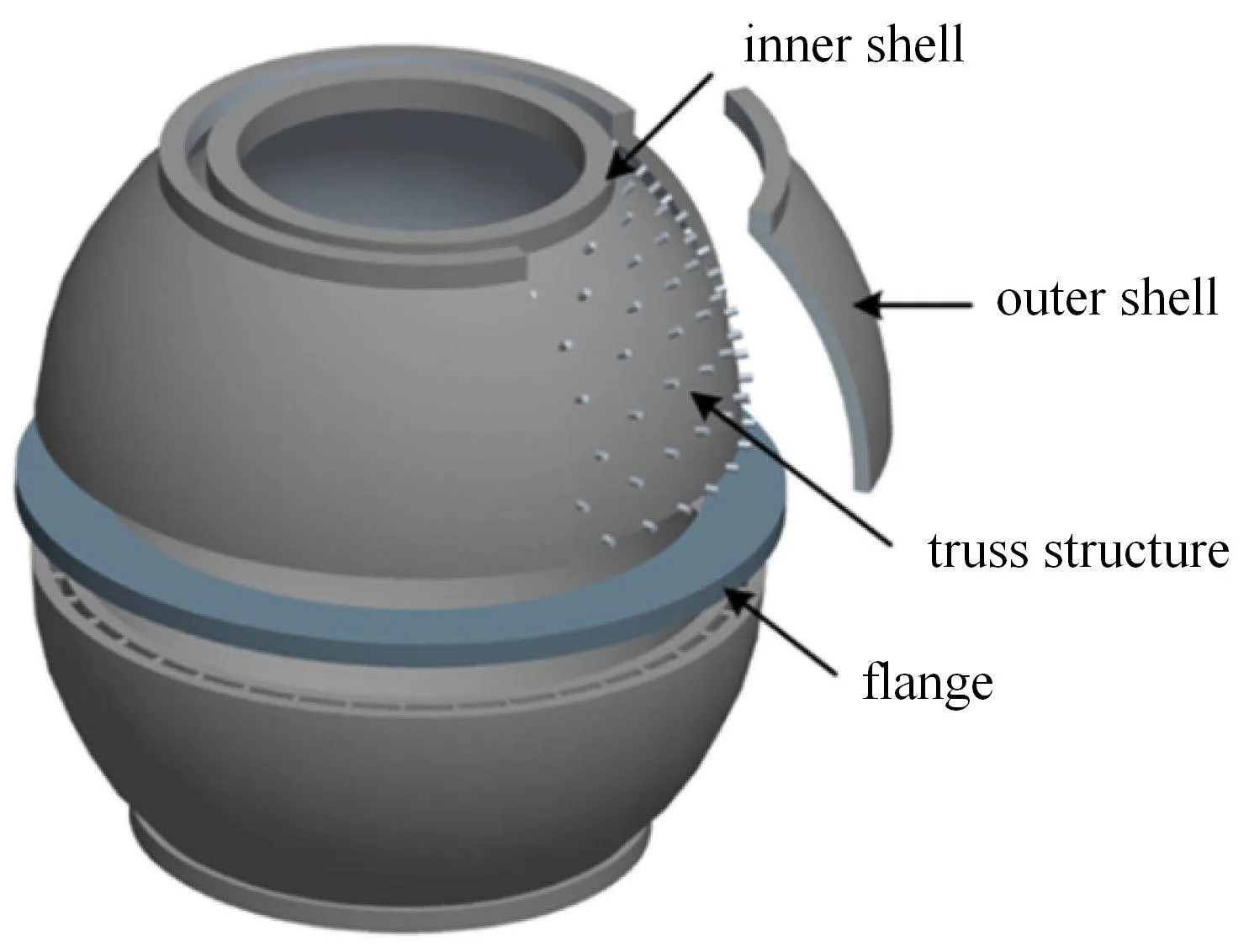
图3 双层耐压壳总体结构示意图Fig.3 The schematic design of a two–layer pressure hull

图4 双层壳设计原理的力学模型Fig.4 Free body diagram of a two–layer pressure hull

使用式(1)和式(2)，可以得到内外壳体沿壳厚度方向的应力分布.计算中，取内部压力Pin为人体正常工作压力 0.1MPa(近似为 1个大气压)，外部压力Pout取100MPa，近似为10000m海深，R取为750mm.将应力分布沿厚度做归一化处理(归一化厚度取为x/t,x为壳厚度方向的坐标,内壁处x=0)，可以得到如图5所示的内外层壳体沿着厚度分布的应力，包括单层和多层壳体在10000m海深环境下的应力分布.采用单层壳，壳体厚度从75mm增加到100mm，可以使得最大Mises应力从约600MPa降低到470MPa，降低了约22%；若采用双层的壳体结构，层间压力取50MPa，层间厚度取10mm，最大应力还能在这个基础上再降低约20MPa.这里的双层壳结构的每层壳的厚度只有单层壳的一半.工艺上讲，厚壳的加工难度高于薄壳.而且精度更难以控制.采用双层壳体结构的另一好处就是降低了对壳体加工的要求.因此，这种结构不仅能够有效缓解内层壁面的应力集中，而且还降低了壳体结构对加工工艺的要求.另外，层间距离δ也是一个设计参数，可以通过调节δ的大小，来实现对结构最大应力的调节，见图6.

图5 单层和双层(层间距离δ=10mm)壳体结构应力分布Fig.5 The comparison between the von Mises stress distributions of one-layer and two-layer pressure hulls(the two layer hull is with interlayer distance of δ=10mm)

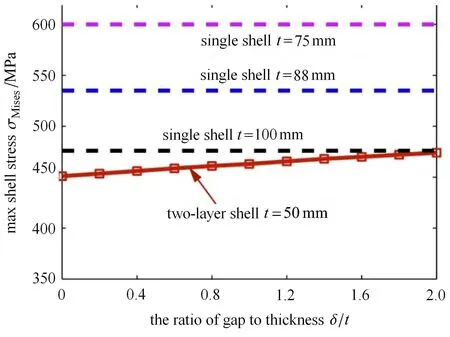
图6 壳体最大应力与层间距离的关系Fig.6 The maximum von Mises stress versus the interlayer distance

2 生物体中的分层分压结构

这里以抹香鲸为例，简述生物为适应深海潜水而进化出来的结构，以对比分层分压的结构设计思想.抹香鲸的生物结构远比双层壳结构复杂，但通过对比，能看到抹香鲸适应深潜的结构和要实现的核心功能是可以和双层壳结构一一对应的.抹香鲸是潜水最深的动物，最大潜深2000∼2200m，时间超过一小时[12-15]，下潜速度最快达到5m/s[12,14].抹香鲸中枢神经所在的头部在下潜过程中更需要保护，于是鲸头进化出了鲸蜡器官(spermaceti organ).鲸蜡 (spermaceti)是位于抹香鲸头部的蜡质，凝固点41◦C∼49◦C.在抹香鲸下潜和捕猎的过程中，肌肉运动发热，体温升高鲸蜡熔化变为液体，作用跟耐压壳层间的液压油一样，可以更均匀地分布压力.图7橙色的部分为抹香鲸的脂肪组织(melon).在图8中可以看到，脂肪组织中的脂肪(标为f)里布满了动脉(标为a)和血窦(图中标为s)，造成了所谓的奇异网(rete mirabile)[13].奇异网的主要作用是收集氮气.高压下，血液中的氮气溶解度升高;低压下，血液中的氮气溶解度降低，这样上浮时，原先溶解的氮气会形成气泡，形成栓塞.这种气栓障碍的形成就是潜水病根源[13].奇异网中的血管通过扩散作用收集了溶解在血液里的氮气，氮气一部分溶解在脂肪里，剩下的就留在奇异网中的血管里，而奇异网血管里血液几乎是不流动的[13].由于大量氮气被奇异网血管收集，这就避免了在抹香鲸脑部血管形成氮气气泡[13].同时由于吸收氮气的缘故，奇异网中的血管和血窦的压力是非常大的，巨大的压力解释了为什么奇异网中血窦尺寸很小的机理[13].抹香鲸调节血压的另一个机制是二氧化碳.抹香鲸潜水时新陈代谢产生的二氧化碳并不排出体外，而用于调节血压，并使得血管扩张，这样可以让鲸蜡和脂肪组织在深海压力下体积只有少量减少，保证抹香鲸上浮时有足够浮力[15].动脉和血窦的作用相当于耐压壳的压力平衡器，调节脂肪组织内的压力.鲸蜡和脂肪组织有两重功能：分压和让压力更均匀地分布.除了鲸蜡和脂肪组织之外，还有其他让压力均匀化的结构.如图7所示，鲸蜡实际并不和鲸鱼颅骨直接接触，之间还有一个叫做前囊(frontal sac)的结构，前囊贴合颅骨，囊内充满液体,可将鲸蜡的压力再次均匀化传递到颅骨.抹香鲸头部的结构为皮肤/肌肉/鲸蜡/脂肪组织/前囊/颅骨的分层结构，实现了分压和压力均匀化的功能，使得颅骨受到的力较小且相对均匀，这样降低了颅骨总体所受应力，避免了局部出现较大应力，保障了颅内中枢神经的正常功能.总而言之，分层分压结构的核心功能就是将外载导致的压力更加均匀地分布到各层，或者更准确地说是降低应力的非均匀分布，避免局部应力过大而导致整体结构失效.

图7 抹香鲸头部正面和侧面的剖面图[15]Fig.7 Anatomy of the sperm whale’s head with the views from the transverse and sagittal planes[15]

图8 抹香鲸脂肪组织的微结构电镜图.脂肪(f)中布满了动脉(a)和血窦(s)形成的奇异网[13].奇异网里的动脉和血窦通过对氮气和二氧化碳的收集，实现了增压和抹香鲸体积少量减少[13,15]Fig.8 Scanning electron microscopy representation of the thoracic rete,after freeze-cracking of the sample in liquid nitrogen,showing arteries(a)and sinusoids(s)embedded in fat(f)[13].The arteries and sinusoids are major components of rete mirabile with the function of collecting nitrogen and carbon dioxide.As a result,the pressure inside rete mirabile increases with a minor decrease of the sperm whale body volume[13,15]

3 结构的屈曲分析

3.1 单层球壳屈曲

对于球壳结构而言，可以根据厚度与半径比将球壳分为薄壳和厚壳两类.一般将厚度与半径比小于0.05的壳体定义为薄壳，大于0.05的则为厚壳[16].相对于薄壳理论/模型而言，厚壳理论要复杂得多，目前对厚球壳应力尚无统一的理论解[16-17].刘涛[17]考虑径向、环向应力形成的应力强度和材料的非线性，推导了厚壳的非弹性失稳压力的简化计算公式.从表1可以看出，除美国“深海挑战者”号的耐压球壳外，其余的所有耐压球壳厚度与半径比均小于0.05，薄壳理论适用，所以这里仅重点介绍薄壳理论.早期经典的球壳屈曲分析在铁木辛柯专著[18]中有很好的综述,对于厚壳的情形，可参考文献[19-20]的分析.对于薄壳模型，存在平截面假定：即垂直于中面的线元在壳变形后仍然和中面垂直并且保持直线.该平截面假定导致的直接结果就是薄壳变形的应变能只由两部分组成：弯曲和中面拉伸的应变能[18].基于该平截面假定，铁木辛柯推导出单层球壳屈曲的临界压力为[18]

式中，E,t,R和v分别为球壳的杨氏模量、厚度、半径和泊松比.忽略上式的第2项，式(3)变为

式(4)即为Zoelly[21]在1915年和Schwerin[22]在1922年分别独立得到的单层球壳屈曲临界压力.以上两个临界压力公式的得出都假设了屈曲模态对称[18].但对称结构在均匀对称的外载作用下是可以发生非对称屈曲的.更具一般性的、考虑对称和非对称屈曲模态的解由Van der Neut[23]在1932年给出.通常认为均匀对称、无几何缺陷的球壳在均匀压力作用下是不会发生非对称屈曲的[18,24].所以，假设对称屈曲模态的式(3)和式(4)被认为是可以用于(无几何缺陷)球壳屈曲压力的计算[18];但需要强调的是一旦有几何缺陷，球壳在均匀压力作用下也可以发生非对称屈曲[25-26].

式(3)和式(4)的推导过程包含如下的假设：扰动无穷小，材料均质，球壳无几何缺陷,应力与应变满足线性关系等.实际上这些假设很难一一满足,式(3)和式(4)的预测值远远高于实验测量值.早期壳体屈曲研究的一个重要内容就是要解释经典理论和实验测量值之间存在巨大差距的问题.在这方面，冯·卡门、钱学森和他们加州理工的同事们做出了系统性和代表性的工作[27-31].他们发展了大挠度非线性和有限挠度扰动的壳屈曲理论来解释理论和实验之间存在巨大差别的问题.当时加州理工大学的水池实验显示球壳屈曲的压力只有式(4)预测的1/4左右[27,31].冯·卡门等[28]发现基于小挠度变形的线性理论总是会过高估计临界屈曲压力；同时他们也发现,对于薄壳而言，即便材料处于弹性范围，其外载与挠度的关系也是强非线性的[27-29].式(4)对应的是线性和无穷小挠度扰动的理论[27].这里的无穷小挠度扰动有两个涵义：(1)结构是完美、无几何缺陷的；(2)其所受扰动是无穷小的.这样的假设是为了保证结构刚发生屈曲时的挠度为零，这也是我们通常遇到的屈曲的情形.冯·卡门等[27]的大挠度非线性和有限挠度扰动的理论显示球壳的屈曲压力有一大一小两个：大的屈曲压力对应的是无穷小挠度扰动的情形，也就是式(4)对应的情形.他们的分析也指出这种通过无穷小挠度扰动达到的大屈曲压力的情形需要对样品加工和实验过程提出极其苛刻的要求才能实现.小的屈曲压力对应的是有限挠度扰动的情形，即球壳屈曲时已经通过突跳获得了一个有限挠度，物理上该扰动可以通过外载变化或者结构的动态效应实现.而且小的屈曲压力对应的就是实际应用的情形，真实结构“倾向于”在较小压力下发生有限挠度屈曲[27].他们的计算结果显示该屈曲压力大约为式(4)预测值的30%，与实验数据的25%基本相符.这样就解释了经典线性无穷小挠度扰动理论和实验数据之间巨大差距的问题.这里需要指出的是这种大挠度非线性和有限挠度扰动的理论是不依赖于初始缺陷的[27]，在不包含初始缺陷的情形下，扰动就使屈曲压力降低了70%.前面提到的初始缺陷也是球壳结构屈曲压力急剧降低[6-11]的最重要的因素之一.冯·卡门和钱学森的工作[28-31]也考虑了这一重要因素.他们的另一重要贡献是研究了壳体的另一种失稳：突跳[28-30].拱或壳结构在压力作用下,其挠度并不一直随压力单调增加，在某个临界压力值(即压力随挠度开始下降时的值)，结构会经历一个突然的变化，构型翻转，跳跃到新的平衡态[32].虽然都是失稳，但屈曲和突跳对应的失稳类型是不一样的：屈曲是叉式分岔失稳，而突跳是鞍点分岔失稳.对于薄壳而言，突跳发生的压力可能远远小于屈曲压力[8].因为突跳伴随着大的位移变化，突跳失稳一旦发生极可能导致整个壳结构失效.钱学森还发展了侧面挂有非线性弹簧的杆受压失稳的模型并给出了近似解析解[31].用侧面挂有非线性弹簧的受压杆模型来研究壳的屈曲最早是由Cox提出的[33],这个模型在壳屈曲的研究中有重要意义.由于壳屈曲的控制方程非常复杂，各量的作用并不清晰;而这个模型，特别是侧面悬挂的弹簧模型，非常直接地给出壳非对称屈曲的物理机制：看似对称的结构实际上是不对称的.壳非对称屈曲的一个直接后果是在变形区域(有限挠度扰动情形下)，非对称屈曲的压力会小于对称屈曲的压力[31].非对称屈曲的临界压力由杆本身的弯曲刚度和侧挂非线性弹簧的刚度共同决定，而弹簧的刚度受结构的初始几何缺陷影响[31].

冯·卡门和钱学森的壳体失稳研究针对的是航空航天器的结构,如火箭、飞机的壳体.而对深潜器耐压结构研究有非常大影响的是20世纪60年代美国海军水面作战中心的以Krenzke为首的先进结构小组[25-26].他们以深潜系统耐压艇体为对象，对多个球壳模型进行了试验研究.Krenzke等进行实验的场所叫做大卫·泰勒模型水池(David Taylor Model Basin).Krenzke等从壳体失稳实验得出的经验公式在国内通常称为泰勒水池公式[16-17].泰勒水池公式如下[17]

这里Es,Et分别为材料的正割杨氏模量和正切杨氏模量，也就是说对于塑性情形，等效杨氏模量换为泰勒水池公式还有如下形式[16]

式中，Cz为制造效应影响系数.我国潜水器规范整球壳屈曲压力计算公式为[16,34]

这里C为半径修正系数，可通过比值t/R查曲线确定；Cs为材料物理非线性修正系数.

各国潜水器耐压壳体设计主要是参照潜艇的设计标准，但由于结构形式、使用条件和材料与潜艇不同,要求亦有所不同.各国规范有很大差别，很多国家甚至没有规范，比如欧盟的结构设计标准ENV 1993-1-6[35]对圆壳屈曲就没有设计规则[8].直接后果就是现今很多船级社均有耐压壳体设计标准，但互相之间差别很大[16].现今，还有研究者不断地提出类似式(5)∼式(7)的屈曲压力公式来作壳体设计的一个指标.比如针对钛合金材料球壳，国内就有数种不同的屈曲压力公式[36-38].文献[16]对这些屈曲压力公式有较好的综述和归纳,这些屈曲压力公式都是考虑了初始缺陷的拟合公式.与式(5)∼式(7)相比，这些新近提出的屈曲压力公式都比较复杂，这里就不一一列出.我国潜水器规范的式(7)与式(5)和式(6)相比有一个共同的系数0.84，可见泰勒水池公式实际是我国潜水器规范的基础.我们这里着重讨论一下泰勒水池公式以及以此为标准可能存在的问题.

泰勒水池公式实际是以式 (4)为基础得出的.Krenzke和Kiernan[25]的17个“近乎完美”圆壳试件的系列实验显示这些“近乎完美”圆壳的屈曲压力最多只能达到式(4)预测值的70%.Krenzke和Kiernan“近乎完美”的定义包含两个方面：(1)加工圆壳产生的残余应力小到可以忽略；(2)圆壳的几何缺陷小到几乎无法测量[25].取泊松比v=0.3[25],压力取70%的上限值，式(4)变为

也就是说式(5)∼式(7)中的0.84系数实际上接近上限值，这就存在过高估计屈曲压力的问题.另外，式(6)和式(7)中的系数Cz和C的物理意义是缺陷的影响，问题更大，因为实际中遇到的缺陷模式各种各样，很难精确标度不同缺陷对壳屈曲压力的影响.理论、计算与实验三者之间差距巨大，实验的不可重复性更是困扰壳屈曲研究的瓶颈问题.通过对“近乎完美”圆壳的研究，Krenzke和Kiernan实际上避开了这个至今仍困扰壳屈曲研究者的问题.

3.2 桁架连接的双层耐压壳屈曲分析

对单层壳的分析表明，球壳这么一个“简单”的结构其实很复杂：非线性导致对称和非对称屈曲模态并存,突跳、有限扰动和缺陷导致屈曲压力下降，以及实验不可重复.为了提高深潜器耐压球壳的屈曲压力，加工精度已经被用到极致来消除几何缺陷，如前所述耐压球壳的真球度已经达到1.003[10].但真球度实质上还是一个总体性衡量几何缺陷的指标，还有其他的几何缺陷，比如球壳厚度的均匀性.一个总的趋势是球壳几何缺陷对屈曲压力的影响随R/t(半径与厚度比)增加而增大：pe/pcr随R/t增大而单调递减[8,39](pe为实验测量的屈曲压力，pcr为式(4)给出的屈曲压力).没有准确标度缺陷影响的模型以及实验不可重复性使得现今的耐压球壳的设计严重依赖于式(5)∼式(7)之类的经验公式.需要强调的是式(5)∼式(7)是基于“近乎完美”的圆壳实验数据建立的，而且这些“近乎完美”的圆壳屈曲压力值是式(4)预测值的42%∼70%,波动幅度；缺陷的存在甚至让屈曲压力值降到预测值的20%以下，使实验结果分散性大[25].除了几何缺陷，还有来自材料本身的缺陷，更有加工过程产生的残余应力、空隙、裂纹等等.虽然这些因素在式(6)和式(7)中有所考虑(比如系数Cz),但坦率地说,这些经验公式是没有坚实的理论和实验数据作支撑的.这也是深潜器单层耐压球壳设计和使用的最大问题.例如，Samuelson和Eggwertz[39]给出的作为圆壳安全设计的屈曲压力极限曲线.该极限曲线给出的是有初始缺陷的圆壳屈曲压力的下限.铝制圆壳的实验数据均在该极限曲线之上，用该极限曲线设计铝制圆壳是安全的；但钢制圆壳的实验数据则是另一番图景了：有相当多的钢制圆壳的屈曲压力低于该极限曲线[8]，因此用该极限曲线来设计钢制圆壳是不安全的.另一个要强调的事实是式(5)∼式(7)只考虑了屈曲，没有考虑突跳.Wunderlich和Albertin对完美无几何缺陷的圆壳的计算显示，在无塑性变形的情形下，完美圆壳的屈曲压力大约为式(4)预测值的80%，如果发生塑性变形的话，完美圆壳在压力仅为式(4)预测值的9%时就会发生突跳[8].桁架连接的双层耐压壳结构设计的目的在于降低缺陷特别是几何缺陷对球壳屈曲压力以及突跳压力的影响.

图9给出桁架连接的双层耐压壳结构的示意图.内外层球壳之间用密排的桁架连接.桁架密排设计的主要目的就是提高球壳屈曲压力和突跳压力.(无缺陷)单层球壳屈曲临界压力正如式(3)∼式(8)给出的一样：几何上是由t/R的比值决定的.屈曲模态也同样由t/R(或者R/t)决定[8].R/t越大，球壳屈曲的波数越大，比如R/t=50时，球壳是以8个傅里叶谐波模态屈曲的；R/t=1000时，球壳是以41个傅里叶谐波模态屈曲的[8].图10给出了R/t=1000时的单层球壳的41个傅里叶谐波模态的截面图.对于薄壳结构，根据定义R/t>200，对于大的R/t值，屈曲的波数就很大.密排桁架的介入相当于加入了约束,阻止此模态的屈曲发生.如果桁架都位于反节点,即上述屈曲谐波变形的波峰和波谷的位置时，向内变形的谐波因为桁架约束，波幅就会被大大抑制住，而不是像图10那样内外对称的，相应的屈曲压力就提高了.对于二维(无桁架支撑的)结构，一些高(共振)频率也会引发如图10所示的大波数变形[40].密排桁架的加入从结构力学上讲相当于给壳结构增加了刚度，有效抵抗大波数的变形.下面对桁架连接的双层耐压壳结构做屈曲分析.

图9 桁架连接的双层耐压壳剖面和带桁架内层壳示意图Fig.9 The cross-section of two-layer pressure hull connected by trusses and a schematic of the inner shell with trusses

图10 R/t=1000的球壳41个傅里叶谐波屈曲模态[8]Fig.10 Buckling mode of a shell with R/t=1000 and 41 Fourier harmonics[8]

如图11所示,由于密排桁架连接的缘故，球壳实际被分割为多个小的亚结构.该亚结构为柱壳，a为柱壳(弧)边长；R为球壳半径；t为球壳厚度.球壳外的水压是pw,壳内压力为po；pw和po的方向为壳曲面法向.

只考虑薄壳的情形，即不考虑壳径向的应力，只考虑环向的应力.环向应力p和面外压力pw和po有如下关系[4]

为了和式 (4)比较，将po设为零.因为薄壳结构t?R，这样式(9)可以近似为

引入如下两个无量纲数[41]

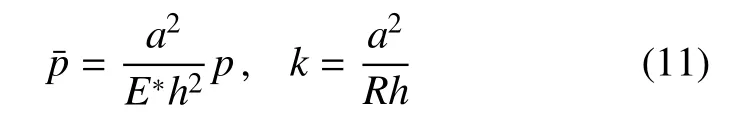
这里，E*=E/(1−ν)为双轴模量；其中E为杨氏模量，ν为泊松比.临界的无量纲屈曲压力为[41]

因为式(12)的第二项是一个小量，可以忽略，这样式(12)就近似为

结合式(10)∼式(12)，得到柱壳亚结构的屈曲压力为

与式(4)的屈曲压力相比，得到

很明显，桁架连接的双层壳中的单个壳要比单层壳抗屈曲性能高的指标就是pw/pcr>1,从式(15)可以看出，这完全是由几何因素决定的：当ν=0.3时，pw/pcr>1对应的几何条件就是这也就是选择密排桁架的原因：a是由桁架数量决定的，数量越多，a越小.增加桁架数量是提高球壳抗屈曲能力的办法.Krenzke和Kiernan[25]用实验方法系统地研究过圆壳亚结构对圆壳整体抗屈曲能力的影响，他们定义了如下的无量纲数

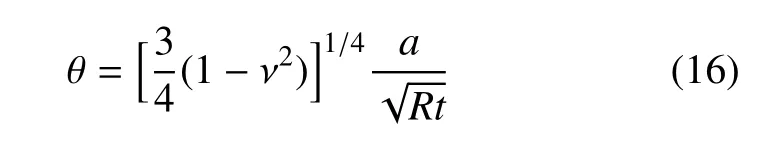
Krenzke和Kiernan[25]发现当θ>2.5时，将圆壳分割成亚结构不但没有增加反而降低了圆壳屈曲压力.也就是说，只有当θ<2.5时才能增加壳屈曲压力.当ν=0.3时，那么θ<2.5对应的就是这和前面得到的是基本一致的.在公式推导的过程中，式(12)是按柱壳结构四边简支计算，四边简支结构的屈曲压力是最小的，实际的结构介于简支和固支之间.但同时，式(12)没有考虑几何缺陷，这两个互相竞争/抵消的因素造成值和Krenzke和Kiernan实验值[25]有6%的差别.理论上讲，如果桁架的密排程度达到时，那么pw/pcr=2,也就是说这时桁架连接的双层壳结构的单壳与同样尺寸、同样材料的单层球壳结构相比，抗屈曲能力提高了一倍,虽然实际加工过程中，增加桁架数量会增加焊接点，会引入一些缺陷从而降低结构的屈曲压力，也会增加结构安装难度.在理论分析层面上讲，增加桁架的密排程度是有效提高双层壳结构屈曲压力的有效途径，同时Krenzke和Kiernan实验也是支持该方法的.

桁架连接的双层壳结构还有一个好处就是降低了甚至还可能消除了壳体突跳失稳.在一些情况下，突跳在远小于结构屈曲压力时就发生[8].突跳和屈曲是两种不同的失稳，有4种情形：(1)屈曲发生而突跳未发生；(2)突跳发生而屈曲未发生；(3)突跳后引发屈曲或屈曲后引发突跳；(4)屈曲和突跳同时发生.如果这两种失稳的压力不一样，就是(1)和(2)的情形;但(3)和(4)的情形目前尚无有效方法确定.实验上，区分情形(1)和(2)极其困难.Krenzke和Kiernan的球壳实验[25]就发生过各种屈曲理论都解释不了的现象，这应该是突跳和屈曲都发生了的情形.Krenzke和Kiernan多次使用的一个词就是“崩塌”(collapse)[25],对于圆壳结构而言，“崩塌”可指上述四种情形的任何一种.突跳的发生不但和结构有关还和载荷有关[32].在同一载荷条件下，“深”(deep)拱和壳比“浅”(shallow)拱和壳要更容易发生突跳，“浅”拱和壳在某些载荷条件下甚至不发生突跳,而“深”拱和壳发生突跳[32].“深”和“浅”是由拱/壳的高度和跨度的比值决定的，比值大的为“深”,比值小的为“浅”[32].如图11所示，“深”的球壳因为被桁架分割变成了“浅”的柱壳了.密排桁架连接在提高抗屈曲能力的同时，也可以消除突跳失稳.

同样，桁架连接的双层耐压壳体的设计也是受到了生物结构启发的：桁架连接的双层耐压壳体的设计即与鹦鹉螺的结构有异曲同工之处.鹦鹉螺的螺壳的剖面图见图12.整个螺壳被隔片分割为大约30个腔室,腔室之间由连室细管连接.连室细管是头足纲目动物特有的长条状组织，通过调节海水中的钠、氯离子浓度产生渗透压梯度，让腔室里的水进出，从而调节鹦鹉螺的浮力[42].鹦鹉螺下沉时，腔室进水但不是充满的，腔室内的压力还稍微低于一个大气压[42]，所以鹦鹉螺的螺壳和我们的耐压壳一样面临着深潜时海水巨大压力的问题.从式(14)可以看出腔室壳的(特征)尺寸(a)越小，那么壳抗屈曲的能力就越大.鹦鹉螺最外的腔室最大，是鹦鹉螺躯体都在这个腔室，而且该腔室是直接与海水相通的，所以不存在抗压力的问题.而其他腔室是与海水隔绝的，存在抗压的问题.所以和最大腔室相比，其他腔室都小得多.在活体鹦鹉螺的压裂实验中，总是最外层的隔片首先失效,因为它的尺寸最大[42].隔片在这里的作用和桁架一样：分割结构，减小结构尺寸，从而提高结构抗屈曲能力.鹦鹉螺还面临一个材料上的挑战：螺壳主要是由碳酸钙组成的.与钛合金和高强度钢相比，碳酸钙杨氏模量较小而且基本上没有延性.鹦鹉螺螺壳材料的微结构类似桁架.图13(a)是鹦鹉螺壳材料微结构的共聚焦显微镜图像，层间有柱状结构支撑；图13(b)是针对图13(a)提出的正方形网格模型[43].同样的这些柱状结构跟我们的桁架一样在材料的微结构层次对结构分割.根据正方形网格模型和鹦鹉螺的活体实验，Sherrard给出了鹦鹉螺壳体材料能下潜的最大深度为[43]

这里D是下潜深度,单位为m，t是微结构层的厚度，r是柱状支撑物间隔的一半[43].式(17)和式(15)具有相似性：结构和材料的抗压能力和间隔(a或r)平方成反比.实验测量的数据显示深海鹦鹉螺的r/t在3.81到5.96之间，平均值为[43]5.43.将上述r/t的值代入式(17)，可算出鹦鹉螺的最大潜深在617m至1508m之间，平均值为743m，这与海洋学家观察到的最大潜深800m是大致相符的[42].

图12 鹦鹉螺壳的剖面图[42]Fig.12 Cross-section of a nautilus shell[42]

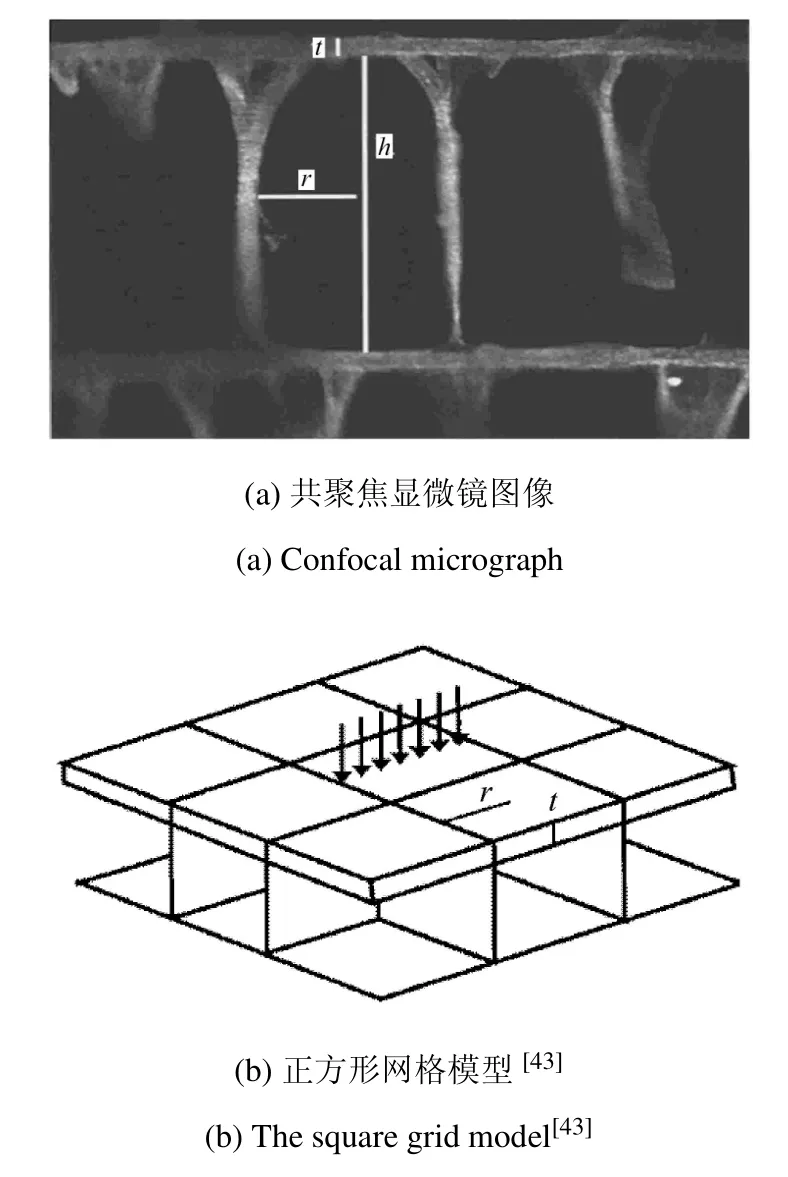
图13 鹦鹉螺壳微结构Fig.13 The microstructure of a nantilus shell

4 结论和展望

桁架连接的分层壳的耐压性能通过两重手段来提高：(1)降低每层壳所受外载,(2)提高每层壳的抗屈曲能力.分层结构是为了实现分压的功能，层间可调控的液压油压将海水压力传递到内层，分别由内外球壳来承担.密排桁架将球壳分解为多个亚结构，以提高结构整体抗屈曲和突跳的能力.对桁架连接的分层结构开展的理论分析和初步的数值模拟表明,该结构与现今的单层耐压壳结构相比有着巨大的抗压优势，是耐压壳结构设计的一个新方向,摆脱了对材料和加工精度的依赖.本文还从结构力学的角度推导了从实验数据总结出来的泰勒水池经验公式，使得深潜器壳体的设计有了更加坚实的力学基础.

1 闫洁.院士解读：海洋研究为何需要超级计算机，科学网2016年8月23日报道(http://news.sciencenet.cn/htmlnews/2016/8/354387.shtm)

2 维基百科：https://en.wikipedia.org/wiki/Bathysphere

3 维基百科：https://en.wikipedia.org/wiki/Bathyscaphe

4 Cook RD,Young WC.Advanced Mechanics of Materials,2nd edn.Upper Saddle River,NJ:Prentice Hall,1999

5 维基百科：https://en.Wikipedia.org/wiki/Deepsea_Challenger

6 Bushnell D.Buckling of shells—pitfall for designers.AIAA Journal,1981,19:1183-1226

7 Blachcut J,Galletly GD.Buckling strength of imperfect steel hemispheres.Thin-Walled Structures,1995,23:1-20

8 Wunderlich W,Albertin U.Buckling behaviour of imperfect spherical shells.International Journal of Non-Linear Mechanics,2002,37:589-604

9 Pan BB,Cui WC.An overview of buckling and ultimate strength of spherical pressure hull under external pressure.Marine Structures,2010,23:227-240

10 刘涛.深海载人潜水器耐压球壳设计特性分析.船舶力学，2007,11(2):214-22(LiuTao.Researchonthedesignofsphericalpressure hull in manned deep-sea submersible.Journal of Ship Mechanics,2007,11(2):214-222(in Chinese))

11 Teng J.Buckling of thin shells:Recent advances and trends.Applied Mechanics Review,1996,49:263-274

12 Tyack PL,Johnson M,Soto NA,et al.Extreme diving of beaked whales.Journal of Experimental Biology,2006,209:4238-4253

13 Blix A,Wallφe L,Messelt EB.On how whales avoid decompression sickness and why they sometimes strand.Journal of Experimental Biology,2013,216:3385-3387

14 Goldbogen JA,Calambokidis J,Shadwick RE,et al.Kinematics of foraging dives and lunge-feeding in fi n whales.Journal of Experimental Biology,2006,209:1231-1244

15 维基百科：https://en.wikipedia.org/wiki/Sperm_whale

16 李文跃，王帅，刘涛等.大深度载人潜水器耐压壳结构研究现状及最新进展.中国造船,2016,57(1):210-221(Li Wenyue,Wang Shuai,Liu Tao,et al.Current status and progress on pressure hull structure of manned deep submersible.Shipbuilding of China,2016,57(1):210-221(in Chinese))

17 刘涛.大深度潜水器耐压壳体弹塑性稳定性简易计算方法.中国造船,2000,42(3):8-14(Liu Tao.Simpli fi ed method of inelastic buckling analysis of deep submersible pressure hull.Shipbuilding of China,2000,42(3):8-14(in Chinese))

18 Timoshenko S.Theory of Elastic Stability,Engineering Societies Monographs.New York:McGraw Hill,1936

19 殷有泉,陈朝伟.软化材料厚壁筒的解析解及其稳定性分析.力学学报,2010,42(1):56-64(Yin Youquan,Chen Chaowei.The analytical solutions of thick-walled cylinder of softening material and its stability.Chinese Journal of Theoretical and Applied Mechanics,2010,42(1):56-64(in Chinese))

20 赵均海,姜志琳,张常光等.不同拉压特性的厚壁圆筒极限内压统一解.力学学报,2017,49(4):836-847(Zhao Junhai,Jiang Zhilin,Zhang Changguang,et al.Uni fi ed solutions of limit internal pressureforthick-walledcylinderwithdi ff erentbehaviourintensionand compression.Chinese Journal of Theoretical and Applied Mechanics,2017,49(4):836-847(in Chinese))

21 Zoelly R.Überein Knickungsproblem am der Kugelschale,Dissertation,Zrich,1915

22 Scherwin E.Zur Stabilitat der dunnwan digen Hohlkugel unter gleichmaβigem Auβendruck.,1922,2:81-91

23 Van der Neut A.De Elastische Stabiliteit van den Dunwandigen Bol,H.J.Paris,Amsterdam,1932

25 Krenzke MA,Kiernan TJ.Elastic stability of near-perfect shallow spherical shells.AIAA Journal,1963,1:2855-2857

26 Krenzke MA.The elastic buckling strength of near-perfect deep spherical shells with ideal boundaries.David Taylor Model Basin Report,1963:1713

27 Von Karman T,Tsien HS.The buckling of spherical shells by external pressure.Journal of the Aeronautical Sciences,1939,7:43-50

28 Von Karman T,Dunn LG,Tsien HS.The In fl uence of curvature on the buckling characteristics of structures.Journal of the Aeronautical Sciences,1940(7):276-289

29 Von Karman T,Tsien HS.The buckling of thin cylindrical shells under axial compression.Journal of the Aeronautical Sciences,1941,8:303-312

30 Tsien HS.A theory for the buckling of thin shells.Journal of the Aeronautical Sciences,1942,9:373-384

31 Tsien HS.Buckling of a column with non-linear lateral supports.Journal of the Aeronautical Sciences,1942,9:119-132

32 Zhang Y,Wang YS,Li ZH,et al.Snap-through and pull-in instabilities of an arch-shaped beam under electrostatic loading.Journal of Microelectromechanical Systems,2007,16:684-693

33 Cox HL.Stress analysis of thin metal construction.Journal of the Royal Aeronautical Society,1940,44:231-282

34 中国船级社.潜水系统和潜水器入级与建造规范.北京：人民交通出版社,2013(China Classi fi cation Society:The construction and classi fi cation rules for the submersible systems and vehicles.Beijing:China Communications Press，2013(in Chinese))

35 Eurocode 3,ENV 1993-1-6,Design of Steel Structures—Parts 1–6:General Rules—Supplementary Rules for the Shell Structures,CEN,Brussels,1999

36 石佳睿,唐文勇.载人深潜器钛合金耐压球壳极限强度可靠性分析.船海工程,2014,43(2):114-118(Shi Jiarui,Tang Wenyong.Ultimate strength reliability analysis of Titanium alloy spherical pressure shell in HOV.Ship&Ocean Engineering,2014,43(2):114-118(in Chinese))

37 王丹,万正权.考虑初始形状影响的耐压球壳临界载荷简化计算公式.船舶力学,2014,18(5):557-564(Wang Dan,Wan Zhengquan.Simpli fi edcalculationformulaforcriticalloadofspherical pressure shell considering the in fl uence of initial shape.Journal of Ship Mechanics,2014,18(5):557-564(in Chinese))

38 Pan BB,Cui WC,Shen YS,et al.Further study on the ultimate strength analysis of spherical pressure hulls.Marine Structures,2010,23:444-461

39 Samuelson LA,Eggwertz S.(Eds.)Shell Stability Handbook.London:Elsevier,1992

40 方奕忠,王钢,沈韩等.环形薄板二维驻波的研究.力学学报,2015,47(4):664-671(Fang Yizhong,Wang Gang,Shen Han,et al.The research of 2-dimensional standing waves on annular plate.ChineseJournalofTheoreticalandAppliedMechanics,2015,47(4):664-671(in Chinese))

41 Chajes A.Principles of Structural Stability Theory.Upper Saddle River,NJ:Prentice Hall,1974

42 维基百科：https://en.wikipedia.org/wiki/Nautilus

43 Sherrard K.Cuttlebone morphology limits habitat depth in eleven speciesof sepia(Cephalopoda:Sepiidae).BiologicalBulletin,2000,198:404-414

NEW STRUCTURAL DESIGN OF SPHERICAL PRESSURE HULL FOR DEEP-SEA SUBMERSIBLES:A MULTILAYER AND PRESSURE REDISTRIBUTION APPROACH1)

Zhang Yin*,†,2)Liu Xiaoming*,†Lei Xianqi*,†Sun Chengqi*Fang Xin*Wei Yujie*,†
*(State Key Laboratory of Nonlinear Mechanics，Institute of Mechanics，Chinese Academy of Sciences，Beijing100190，China)
†(School of Engineering Science，University of Chinese Academy of Sciences，Beijing100049，China)

The pressure hull is the most important key structure to a deep-sea submersible,whose safety and overall performance depend on the integrity of the pressure hull.The current single shell design of the pressure hull is reviewed and a new design based on the multilayer and pressure redistribution mechanism is also proposed in this study.The design is inspired by two deep-sea animals of sperm whale and nautilus.The two mechanisms,the multilayer structure of sperm whale and the shell substructure divided by the septa of nautilus,are synthesized in the design to improve the pressurebearing capacity of the hull.Compared with the one layer structure of the pressure hull,the new design increases both the structural strength and buckling load.Furthermore,the new design can also signi fi cantly improve the overall performance of the deep-sea submersible by enlarging the hull volume,enhancing its reliability and lessening the technical challenges of fabricatingultra-thick shell structure.Because the truss structure is introduced in the newshell design,which e ff ectively divides a spherical shell into several substructures of cylindrical shell,a formula is strictly derived to evaluate the truss e ff ect on the buckling load bearing capability of a cylindrical shell.The di ff erence between the newly derived formula and the formula of the Taylor basin,which is summarized from the experimental data and widely used as a standard for the current design of submersible shell,is only 6%.Furthermore,this new derivation also lays a solid theoretical foundation for our new shell design.

pressure hull,deep-sea submersible,structure,strength,buckling

U674.941

A doi：10.6052/0459-1879-17-156

2017–05–04 收稿，2017–09–20 录用,2017–09–28 网络版发表.

1)中国科学院B类战略性先导科技专项(XDB22020201)和国家自然科学基金(11372321,11772335)资助项目.

2)张吟，研究员，主要研究方向：振动，固体力学中的表界面效应.E-mail:zhangyin@lnm.imech.ac.cn

张吟,刘小明,雷现奇,孙成奇,方新,魏宇杰.基于分层分压结构的新型潜水器耐压壳结构设计.力学学报,2017,49(6):1231-1242

Zhang Yin,Liu Xiaoming,Lei Xianqi,Sun Chengqi,Fang Xin,Wei Yujie.New structural design of spherical pressure hull for deep-sea submersibles:A multilayer and pressure redistribution approach.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1231-1242