固体结构大规模矩阵正定性判定的快速算法1)

徐 辉 刘 彬

(清华大学航天航空学院工程力学系应用力学教育部重点实验室,北京 100084)

固体结构大规模矩阵正定性判定的快速算法1)

徐 辉 刘 彬2)

(清华大学航天航空学院工程力学系应用力学教育部重点实验室,北京 100084)

对于结构稳定性分析中超大规模矩阵正定性判定,必须采用并行计算方法,传统方法如计算特征值、主子式行列式及LDLT等直接方法难以实现.本文提出了一些可适用于并行的迭代判定算法.借鉴力学系统中能量下降的思想,发展了一种判定矩阵正定性的新思路,即将矩阵的正定性判定问题转化为一个优化问题,并基于优化算法来判定矩阵的正定性.提出了基于最速下降法和共轭梯度法来进行矩阵正定性判定的算法.然后考虑到力学系统刚度矩阵的稀疏性和结构刚失稳状态的弱非正定性,提出可以先截超平面后解方程求驻值点的方法来判定弱非正定矩阵的正定性.为了保证对强非正定矩阵判定的准确性,本文提出可以高效混杂使用截平面法和共轭梯度法.数值实验结果表明,本文提出的算法具有准确性和高效性.对于强非正定矩阵而言,共轭梯度算法更加高效;而对于弱非正定矩阵,则是截平面法和混杂算法更加高效.这些算法都容易在机群上实现并行计算,能够快速判定大规模矩阵的正定性.

矩阵,正定性,共轭梯度法,截平面

引言

在力学问题中,对系统稳定性的判定非常重要,例如在固体力学问题中,通常需要判定结构的稳定性,而系统的稳定性和系统刚度矩阵的正定性直接相关.对系统的刚度矩阵进行正定性判定,可以直接从在理论上来推测结构稳定性.

对矩阵的正定性进行判定也是一个经典的数学问题.Johnson[1]在1970年提出实正定矩阵的概念及一些判定准则.很多学者对正定矩阵的性质展开了研究工作和总结[2].

经典的判定矩阵的正定性方法主要通过两种途径来实现[3-4].第一是从标准型上出发,有若干等同的表述:矩阵K的特征值全大于零,则矩阵K正定;矩阵K与n阶单位矩阵En合同,则矩阵K正定;存在可逆矩阵S,使得K=STS,则矩阵K正定等等.第二是从主子式上出发,也有若干等同的表述:矩阵K的所有主子式全大于零,则矩阵K正定;矩阵K的所有顺序主子式全大于零,则矩阵K正定等等.

近年来,学者对矩阵正定性的判定展开了一些研究工作.有一些工作基于矩阵分解和变换来判定矩阵的正定性:三角及对角阵LDLT分解和Cholesky分解算法常用于矩阵正定性的判定.李伟[5]通过对矩阵进行初等保号变换,将矩阵转化为三角矩阵并判断其中元素的正负来判定原矩阵的正定性.赵淑贤等[6]通过合同变换,证明n阶矩阵的正定性可以由n– 1阶矩阵的正定性来进行确定,提出使用降阶的方法来判定矩阵的正定性.

另有一些部分工作从矩阵的特征值分步的角度来展开.Gerschgorin圆盘定理可用于估计矩阵的特征值分布[7].基于圆盘定理,邹黎敏等[8]通过比较包含所有特征值的圆盘半径和圆心到原点的距离,基于优化理论来判定矩阵的正定性.岑燕斌等[9]基于圆盘定理、半正定矩阵的满秩分解和主对角线严格占优判别法,提出极大极小元矩阵正定性判定算法.Sorensen[10]提出使用Arnoldi法来进行多项式滤波,该方法可以用于直接求解矩阵的最小特征值,对矩阵的正定性进行判定.

在有限元问题中,系统的刚度矩阵通常具有很大的规模.当矩阵规模变大之后,使用经典的判定算法所需计算量快速加大,并且这类算法都基于单机开发,难以实现并行化.这时将难以再使用经典的判定方法来判定大规模矩阵的正定性.本文将提出和探讨几种更适合于大规模并行计算框架下矩阵的正定性判定算法.

1 矩阵正定性判定的快速算法

1.1 算法思想的提出

矩阵K的正定性的数学表示是若对于任意的非零列向量x,xTKx始终大于零,则矩阵K是一个正定矩阵.若需判定一个不对称矩阵的正定性,可以转化为判定一个对称矩阵K的正定性,其中

因此下文所讨论的矩阵都是对称矩阵.如前所述,固体力学结构或系统的稳定性与其刚度矩阵的正定性是等价的.因此提出一类算法,为了判定刚度矩阵K的正定性,可以来研究其对应结构的稳定性.具体来说,对于一个n阶矩阵K,可以假定“系统的平衡位置”为x0=0,在此基础上,外界施加一个“扰动”x,其中x是一个n维列向量并代表偏离平衡位置量.之后模拟“系统能量”的下降过程,即使xTKx的数值不断减小,来模拟力学结构受到扰动后的演化情况,若经过一段时间之后,“系统回到平衡位置”,即x=x0=0,则系统是稳定的,矩阵是正定的.若经过一段时间之后,“系统偏离原来的平衡位置”,即xTKx<0,则系统是不稳定的,即矩阵是非正定的.

因此对矩阵正定性进行判定可以转化为一个优化问题.借鉴上述力学系统中能量下降的思想,可以基于优化理论对矩阵正定问题进行判定,即

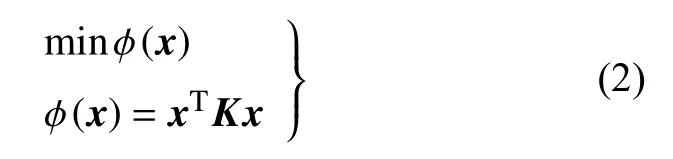
其中,ϕ(x)为目标函数,x为优化变量.求解上述优化问题,若经过一系列的计算之后,能够找到一个x,使得xTKx<0,则矩阵是非正定的;若能够找到一个x≠ 0,但xTKx=0,则矩阵是半正定的;若经过大量的计算,始终找不到一个x,使得xTKx<0,则矩阵是正定的.

下文将基于优化理论提出迭代算法来判定矩阵的正定性.给定一个初始扰动,即迭代初值x1之后开始迭代.随着迭代过程的进行,目标函数的数值不断下降.在将要进行第i次迭代时,优化变量为xi,迭代结束后,优化变量为xi+1.迭代过程中优化变量满足如下关系

其中,hi为第i次迭代的前进方向,α为前进步长.

1.2 基于最速下降法的算法一

首先,基于优化理论[11]中的最速下降思想(steepest descent method,SD),提出矩阵正定判定算法一.使用最速下降法进行迭代的示意图如图1所示.使用最速下降法进行求解优化问题(2),每次优化变量的前进方向是当前的梯度下降方向,在力学系统中,这相当于对一个无惯性效应的系统进行动力学显式计算,每次位移将沿着局部不平衡力的方向进行演化.随着演化的进行,系统的能量逐渐降低.这也是将最直接的最具力学意义的想法进行算法实现.

图1 最速下降法迭代示意图Fig.1 Schematic of steepest descent method

迭代过程中优化变量的前进方向即是目标函数梯度的反方向,此时目标函数的梯度方向为

其中,gi为优化变量所处位置目标函数值梯度的负方向.

迭代算法的计算量和优化变量前进步长的选取直接相关.若迭代步长选取的过小,每一次下降的会准确,但是会导致计算量的大幅度增加;若迭代步长选取的过大,在一定程度上,可能导致更快的收敛,但是也可能出现越过极值点而导致的重复计算,同样造成计算量的增加.建议按如下方式选取α,使得在沿着当前的前进方向hi上,目标函数

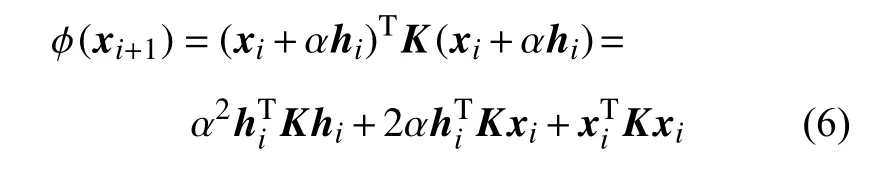
达到极小值.此时目标函数值是一个关于α的二次函数.当时,抛物线开口向上,取

此时α使目标函数值ϕ(xi+1)关于α达到极小值,若ϕ(xi+1)>0 暂时不能判定矩阵是否正定,需继续迭代;而当时,此时目标函数的最小值可趋向–∞,可以显示矩阵K为非正定的.

下面讨论算法迭代结束的终止条件,推荐使用如下3个终止准则.

终止准则一:若能够计算得到一个非零列向量x,满足

则此时判定矩阵非正定,迭代终止.

终止准则二:到达最大的迭代次数

若随着迭代的进行,迭代次数i到达算法容许的最大迭代次数imax,仍然没有找到非正定方向x,使得xTKx<0,则此时认为矩阵是正定的.算法容许的最大迭代次数imax通常和矩阵规模有关,矩阵规模越大,所需的迭代次数越多.在后文的测试算例中,选取imax=2n.

终止准则三:优化变量方向变化不大

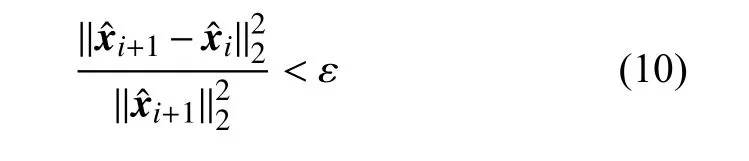
算法的实现过程中主要涉及到矩阵向量乘运算,算法复杂度为O(n2).

1.3 基于共轭梯度法的算法二

需要指出的是,直接基于最速下降法来进行迭代计算,在靠近目标函数极值点的附近,总是曲折前进,优化的效果往往不好,算法收敛速度较慢[10].为了避免这个问题,可以基于前后两次迭代的前进方向相互共轭的思想,对前进的方向进行修正,使用共轭梯度法 (conjugate gradient method,CG)来判定矩阵的正定性,该方法考虑了上一次的前进方向对此次前进方向的影响,算法的收敛速度将大幅度的加快.在此基于共轭梯度法,提出矩阵正定性判定算法二.使用共轭梯度法进行迭代的示意图如图2所示.

图2 共轭梯度法迭代示意图Fig.2 Schematic of conjugate gradient method

前进方向落在当前梯度方向和前一次前进方向张开的空间中,满足

其中β为权系数,将通过共轭方向来确定:前后两次的前进方向满足

此时解有

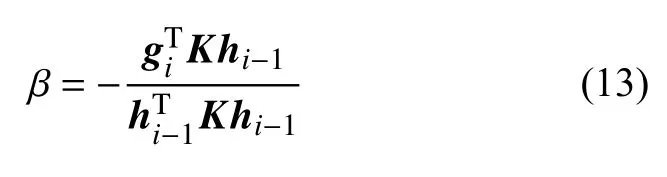
基于共轭梯度算法确定的前进步长和终止准则与最速下降法一致,将由式(7)～式(10)决定.

可以证明,由共轭方向确定的前进方向和前进步长,在当前梯度方向和上一次迭代的前进方向张开的空间中最优的.即通过共轭梯度法确定的α,β满足

对于规模为n二次优化问题,在理论上使用共轭梯度法迭代n次可以即找到最优解.为了保险起见,选取最大迭代次数imax=Sn,其中S为大于 1 的安全因数.算法的实现过程中涉及到矩阵向量乘运算,算法复杂度为O(n2).

1.4 基于截平面的算法三

另一方面,在实际问题中,经常需要对弱非正定矩阵进行分析.例如在固体力学的问题中,在一个结构是稳定的时候,其刚度是正定的.随着载荷的增大,结构出现失稳.当结构刚刚出现失稳时,其刚度矩阵一般只有唯一且非常小的负特征值.此时矩阵非正定的非常不明显.如果通过最速下降算法或者共轭梯度法来进行求解的时候,很可能需要迭代非常多次,才能够判定矩阵是非正定的,随着负特征值的绝对值越小,通过若干次搜索找到相应的非正定方向x越困难.因此需要开发一种对弱非正定矩阵有着较好的性能的算法.

这种情况下,提出使用截平面的思想来进行矩阵正定性的判定:在一个n维空间截一个超平面,在这个n–1维的超平面上寻找是否存在一个使得xTKx<0 的点,若存在,则该矩阵非正定;若不存在,则矩阵正定.若系统稳定性刚刚发生转化,转变为一个不稳定的系统,此时其刚度矩阵只有一个非常小的负特征值.此时只有沿着某一个特定的方向,目标函数xTKx才小于0,如图3空间中细椭圆锥所示.所截的这个超平面内只有一小块区域(即图3中蓝色区域)xTKx<0,此时其中必包含一个极小值点,当然也是超平面上函数xTKx的驻值点.

综上所述,对于弱非正定矩阵的判定,提出可以先截取一个超平面然后求其驻值点.并称这第三种算法为截平面法 (cutting plane method,CP).具体做法是,选择一个不通过原点的超平面,其过原点的法向量记为d,则该超平面可以表示为对于弱非正定矩阵而言,认为所截的超平面上的点的极小值点就是驻值点.因此构建拉格朗日函数

图3 针对弱非正定矩阵的截平面法示意图Fig.3 Schematic of cutting plane method for weak non-positive definite matrix

其中λ为拉格朗日乘子,对上式取驻值有

求上述超平面的驻值问题转化为一个n+1维的线性方程组求解问题,其解x就对应于驻值点.由于该线性方程组的系数矩阵满秩,因此有唯一的解或驻值点存在.若刚度矩阵只有一个小负特征值的时候,如图3所示,此时该驻值点x将极有可能是超平面中目标函数的极小值点,所以用这个方法一次求解就可以发现非正定方向.

需要指出的是,固体结构求解中的线性方程组矩阵K一般是稀疏的,而易知式(17)中的系数矩阵依然稀疏,充分利用矩阵的稀疏性,可以使算法复杂度接近O(n).在求解式(17)的线性方程组的过程中,如果是超大规模的问题则必须采用并行算法来求解,但线性方程组直接解法(如LU分解或LDLT分解)的并行求解规模难以扩大而不能被采用,因此这些直接算法无法用于确定矩阵的正定性,需采用更适用于并行的迭代算法,如多级平衡的并行求解器[12].

需要说明的是,截平面法对于一些弱非正定的矩阵一般比较有效.倘若超平面(或法向量d)选取不当,或者系统不稳定方向的圆锥开口较大时,如图 4所示.此时超平面内xTKx<0的区域如图 4中蓝色区域所示,xTKx>0 的区域如图 4 中浅黄色区域所示,此时超平面上函数xTKx的驻值点将不再是极小值点,此时仅仅通过截平面求驻值点来判定矩阵的正定性可能会失效.在实际的应用中,为了判定一个弱非正定矩阵的正定性,为了保险起见,可以截多个超平面来进行测试,这样就更有可能超平面上的驻值点就是极小值点,以保证截平面法求解的准确性.

图4 针对强非正定矩阵的截平面法示意图Fig.4 Schematic of cutting plane method for strong non-positive definite matrix

1.5 算法四: 高效混杂使用上述算法

如前所述,前面各种方法都有优缺点和较适用的情形.如对于一些强非正定矩阵而言采用截平面法时,可能需使用多个法向量来测试才能使得超平面上的驻值点为极小值点.为了避免这种弊端,可以把截平面法和共轭梯度法相结合:固定优化变量只能在所截的超平面附近运动,把对矩阵正定性的判定问题转化为一个优化问题,首先使用截平面法来确定迭代的初值,再使用共轭梯度法来迭代求解.这样可以同时保证对弱非正定矩阵进行判定的高效性,及对强非正定矩阵判定的准确性.在此基于截平面法 (cutting plane method,CP) 和共轭梯度法(conjugate gradient method,CG)提出混杂算法四(CP&CG),按以下三部分论述.

1.5.1 优化问题的提出

假设存在一个向量x,其末端落在所截超平面中,则向量x–d是这个平面中的向量,故原来的式(1)对应的无约束优化问题转化为一个有约束的优化问题

使用罚函数法对该问题进行求解,把有约束优化问题转化为无约束优化问题

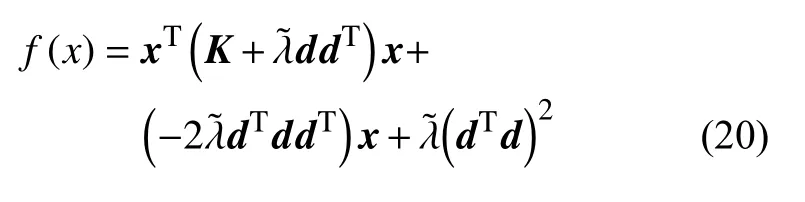
1.5.2 迭代初值的选取

一个好的迭代初值可以使目标函数值快速下降,使用更少的迭代次数就能达到较小的目标函数值.迭代的初值将选取在所截超平面的驻值点上,即由截平面法通过求解式(17)得到.

1.5.3 优化问题求解

经过求解式(17)对应的线性方程组,找到了一个较好的迭代初值,这将使后续的优化计算有更加快速的收敛速度.倘若此时超平面上的驻值点是极小值点,迭代的初始值处xTKx<0,此时就不再需要使用共轭梯度法进行后续的迭代,可以直接判定矩阵是非正定的,此时CP&CG算法即退化为CP算法.倘若此时超平面上的驻值点不是极小值点,如图4所示,则使用共轭梯度法进行后续的迭代,寻找在超平面附近是否存在使得xTKx<0的点.

2 算法性能测试

前文提出了4种判定矩阵正定性的快速算法:基于最速下降法的算法一(SD)、基于共轭梯度法的算法二(CG)、基于直接截平面的算法三(CP)和混杂算法四(CP&CG).在本节中,将生成不同类型的矩阵,来测试这些算法的性能.考虑到力学系统中总体刚度矩阵稀疏的特点,分别讨论算法对稠密矩阵和稀疏矩阵的性能.

2.1 测试所用矩阵的生成方法

使用三个指标来衡量测试所用的对称矩阵:矩阵规模n、负特征值比例p和负特征值大小指标q.测试所用的对称矩阵通过下式生成

其中W是大小为n×n随机矩阵,其中的每一个非零元素在[–0.5,0.5]之间服从均匀分布.D是大小为n×n的对角矩阵,D中元素分成两类,一类为正数,大小为 1,一类为负数,大小为q.

当负特征值比例p=0时,对角阵D中所有元素都是正数,此时生成的测试矩阵K是正定的.当负特征值比例p=1时,对角阵中的所有元素都是负数,此时矩阵所有特征值都是负数,此时生成的测试矩阵是负定的.在负特征值比例p∈(0,1)时,测试矩阵K是非正定的,此时负特征值比例p越小,负特征值大小指标q的绝对值越小,矩阵非正定的越不明显.

若随机矩阵W是一个稠密矩阵,经过式(21)得到测试矩阵也是稠密的.在力学问题中,系统的刚度矩阵往往是稀疏的,选取稀疏的矩阵作为随机矩阵W,经过式(21)得到的测试矩阵也是稀疏的.本文测试所用的稀疏矩阵每一行中非零元素占比约为10%.

2.2 强非正定矩阵测试结果

下讨论3种算法对非正定矩阵的测试结果,并和经典的分解算法LDLT进行对比.

选取负特征值比例p=0.5,负特征值大小指标q=-1,随机生成一系列强非正定矩阵进行测试.测试矩阵的规模为 256 阶,重复试验 1 000 次,选择算法参数几种算法的测试结果如表1所示.由于截平面算法CP主要针对弱非正定矩阵,此时不再对该算法进行测试.

从强非正定矩阵测试结果可以看出,SD算法耗时最短,CG 算法其次,CP&CG 算法随后.SD 与CG算法用时相近,明显短于CP&CG算法.这是对强非正定矩阵进行判定时,优化算法迭代几次之后很快就能够找到一个优化变量x,使得xTKx<0,从而判定矩阵是非正定的;而CP&CG算法为了选取一个较好的迭代初始值,需要对一个n+1阶的线性方程组进行求解,这导致了额外的计算量.此时如果直接使用CP算法,超平面上的驻值点一般都不是极小值点,CP算法将会失效,而把共轭梯度法和截平面算法相结合的CP&CG混杂算法保证了对强非正定矩阵判定的准确性.

表1 不同算法对强非正定矩阵的判定结果对比Table 1 Algorithm performance for strong non-positive matrix

对于强非正定矩阵而言,本文提出的基于优化理论的矩阵正定判定算法的耗时远小于经典的LDLT分解算法,我们可以作如下解释:在分解算法的计算过程中,需要把矩阵先进行LU分解,再进行LDLT分解.等到整个分解过程完全结束之后才能够对对角矩阵中的元一一观察,从而判断矩阵是否正定,这整个分解过程相当于把整个矩阵“完全”地分析了,与之不同的是,优化算法通过演化的形式,只需要找到“一个”x,使得xTKx<0,即可给出判定结果.与分解算法的“完全”分析相比,优化算法的“局部”分析显然更加的快速,固在大规模情况下,优化算法的计算效率将会更高.

2.3 弱非正定矩阵测试结果

下面讨论这些算法对弱非正定矩阵的测试结果,并和经典的分解算法LDLT进行对比.

随机生成一系列弱非正定矩阵来进行测试,对角阵D中只有一个元素是负数,负特征值大小指标q= -10–5,这使得测试的矩阵只有唯一特别小的特征值.测试矩阵的规模为256阶,重复试验1000次,选择算法参数S=2,ε=1×10–12,几种算法的测试结果如下表2所示.对弱非正定矩阵而言,由于CP&CG混杂算法直接求解线性方程组作为迭代初值之后即可以判定矩阵的正定性,不再需要进行后续的优化迭代,此时CP&CG算法退化为CP算法,因此不再需要对单独CP&CG算法进行测试.

表2 不同算法对弱非正定矩阵的判定结果对比Table 2 Algorithm performance for weak non-positive matrix

从表2中可以看出,对于弱非正定矩阵而言,LDLT,CG和CP算法仍然能够准确的判定其正定性,而SD算法由于其较慢的收敛速度而失效.此时最优的是CP算法,其通过求解n+ 1阶的线性方程组,通过计算超平面上的驻值点来寻找超平面上极小值点,直接判定出矩阵的正定性.而CG算法则需要迭代很多次之后才能找到一个优化变量x,使得xTKx<0,从而判定矩阵的正定性,并且矩阵的负特征值越小,使用CG算法来寻找非正定方向就更加的困难.

与稠密矩阵相比,稀疏矩阵由于其进行矩阵向量乘法和线性方程组求解的时候所需的计算量更少,此时优化算法的计算效率加快.

2.4 测试结果讨论

综上所述,最速下降算法SD由于其收敛速度较慢,对于一些弱非正定矩阵不能准确的判定,在实际运用中舍去.截平面法CP对弱非正定矩阵进行判定时有很好的性能,可以和共轭梯度法混杂一起使用,以保证对强非正定矩阵的判定的准确性.不管是稠密矩阵还是稀疏矩阵,共轭梯度算法和混杂算法对矩阵的正定性进行能够准确的判定.对弱非正定矩阵而言,混杂算法CP&CG有着更好的性能;对强非正定矩阵而言,共轭梯度法CG有着更好的性能.

共轭梯度算法、截平面算法和混杂算法都容易进行程序的编写.同时算法涉及的主要的操作是矩阵向量乘法和线性方程组的迭代求解计算,对于一些大规模的问题容易实现并行化.需要指出的是,在力学问题中,系统的刚度矩阵往往是非常稀疏的.此时求解大规模的线性方程组的算法复杂度接近O(n).并且当结构将要发生失稳的时候,系统的刚度矩阵只有一个很小的负特征值.此时对于弱非正定系统而言,此时使用截平面算法CP和混杂算法CP&CG来进行判定矩阵的正定性将会更加地高效.

3 结论

本文主要探讨了对于固体结构分析中超大规模矩阵的正定性判别算法,由于必须采用并行算法,所以一些如求特征值或LDLT分解算法都无法适用,因此探讨了一些可以用于迭代并行的算法.主要结论如下.

(1)借鉴力学系统中能量下降的思想,提出一种判定矩阵正定性的新思路,即将矩阵的正定性判定问题转化为一个优化问题.并基于优化理论提出二种判定矩阵正定性的快速算法:最速下降法和共轭梯度法.

(2)考虑到力学系统中,结构刚刚失稳状态时的刚度矩阵的稀疏性和弱非正定性,提出截平面法来判定矩阵的正定性,即先截超平面后求解线性方程组找驻值点.

(3)提出可以混杂使用共轭梯度法和截平面法,在高效判定弱非正定矩阵正定性的同时,保证对强非正定矩阵的判定准确性.

(4)共轭梯度算法能够更加快速的判定强非正定矩阵的正定性.截平面法和混杂算法能够更加快速的判定弱非正定矩阵的正定性.

1 Johnson CR.Positive definite matrices.American Mathematical Monthly,1970,77(3):259-264

2 Bhatia R.Positive Definite Matrices.New Jersey:Princeton University Press,2015

3 屠伯埙,徐诚浩,王芬.高等代数.上海:上海科学技术出版社,1984(Tu Boxun,Xu Chenghao,Wang Fen.Advanced Algebra.Shanghai:Shanghai Science and Technology Press,1984 (in Chinese))

4 张禾瑞,郝炳新.高等代数.第4版.北京:高等教育出版社,2001(Zhang Herui,Hao Bingxin.Advanced Algebra.4th ed.Beijing:Higher Education Press,2011(in Chinese))

5 李伟.关于正定矩阵判别定理的改进.高等数学研究,2007,10(6):42-43(Li Wei.Improvement of positive definite matrix discriminant theorem.Studies in College Mathematics,2007,10(6):42-43(in Chinese))

6 赵贤淑,杨莉军.正定矩阵的降阶判别法及其应用.北京印刷学院学报,2000(2):40-43(Zhao Xianshu,Yang Lijun.Dicrimination method of reduction of order of positive definite matrix and its application.Journal of Beijing Institute of Graphic Communication,2000(2):40-43(in Chinese))

7 Varga RS.Geršgorin and His Circle.Berlin Heidelberg:Springer 2004

8 邹黎敏,胡兴凯,伍俊良.正定矩阵的性质及判别法.中山大学学报自然科学版,2009,48(5):16-23(Zou Limin,Hu Xingkai ,Wu Junliang.The properties and discrimination of the positive definite matrices.Acta Scientiarum Naturalium Universitatis Sunyatseni,2009,48(5):16-23(in Chinese))

9 岑燕斌,韦煜,罗会亮.快速判断一类实对称矩阵正定的极大极小元方法.北京交通大学学报,2011,35(6):140-143(Cen Yanbin,Wei Yu,Luo Huiliang.Max and mini-element method:A rapid determination of one class rear symmetric positive definite matrices.Journal of Beijing Jiaotong University,2011,35(6):140-143(in Chinese))

10 Sorensen DC.Implicit application of polynomial filters in a k-step Arnoldi method.Society for Industrial and Applied Mathematics,1992

11 Boyd,Vandenberghe,Faybusovich.Convex optimization.IEEE Transactions on Automatic Control,2006,51(11):1859

12 Xu R,Liu B,Dong Y.Scalable hierarchical parallel algorithm for the solution of super large-scale sparse linear equations.Journal of Applied Mechanics,2012,80(2):a111-121

FAST ALGORITHMS FOR DETERMINING POSITIVE DEFINITENESS OF LARGE SCALE MATRICES IN SOLID STRUCTURE ANALYSIS1)

Xu Hui Liu Bin2)
(AML,Department of Engineering Mechanics,Tsinghua University,Beijing100084,China)

In order to determine the positive definiteness of the super-large-scale matrix in the structural stability analysis,the parallel computing method must be adopted.However,the traditional direct methods such as the eigenvalue’s analysis,the master subordinate determinant’s computation and LDLT decomposition are difficult to realize in parallel computing.In this paper,some iterative algorithms which are suitable for parallel computing are proposed.A new approach is developed that determining the positive definiteness of a matrix can be transformed into an optimization problem,which is solved by various optimization algorithms.The algorithms based on the steepest descent method and the conjugate gradient method are proposed.Considering the sparseness of the stiffness matrix of the mechanical system and the weakly non-positive definite property of at the critical buckling state,we propose a method via calculating the stationary point on a cutting plane to determine the non-positive definite matrices.In order to ensure the accuracy of the determination of strong non-positive definite matrices,a hybrid method combing the cutting plane method and the conjugate gradient method is developed.The numerical results show that the proposed algorithms are accurate and efficient.The conjugate gradient algorithm is more efficient for strongly non-positive definite matrices while the hybrid method is more efficient for the weak non-positive definite matrices.These algorithms are easy to realize in parallel computing on the cluster and can quickly determine the positive definiteness of large-scale matrices.

matrix,positive definite,conjugate gradient method,cutting plane

O346.1

A

10.6052/0459-1879-17-292

2017–08–26 收稿,2017–11–15 录用,2017–11–15 网络版发表.

1)国家自然科学基金资助项目 (51232004,11372158,11425208).

2)刘彬,教授,主要研究方向:大规模多尺度多物理场计算、复合材料力学和断裂力学.E-mail:liubin@tsinghua.edu.cn

徐辉,刘彬.固体结构大规模矩阵正定性判定的快速算法.力学学报,2017,49(6):1223-1230

Xu Hui,Liu Bin.Fast algorithms for determining positive definiteness of large scale matrices in solid structure analysis.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1223-1230