图形翻折类中考题解析

江苏省无锡市港下中学 程 军 (邮编：214199)

图形翻折类中考题解析

江苏省无锡市港下中学 程 军 (邮编：214199)

2017无锡中考落下帷幕,对于试卷第10题,在阅卷过程中,同行们普遍认为题目入口宽、解法多样、精彩,体现数学本质,是一道充满数学味的试题,现摘录如下.

题目 (2017无锡中考第10题)如图,△ABC中,∠BAC＝90°,AB＝3,AC＝4,点D是BC的中点,将△ABD沿AD翻折得到△AED,则线段CE的长等于( )

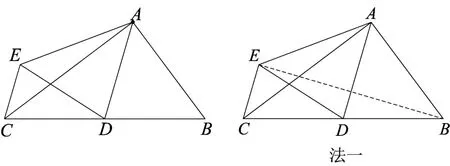
1 解法展示

1.1 解法一

解题透视 为什么会想到连接BE?如何求BE长?△ABD与△AED关于AD对称,观察B、E是对称点,联想BE被AD垂直平分;另一方面DE＝DB＝DC,容易联想到产生Rt△;至于如何解决BE长,可以采用面积法,也可以采用求其一半(用相似).

解后反思为何如此考虑?基于轴对称性,发现DB＝DE＝DC,构造直角三角形.

1.2 解法二

解题思路 连接BE,设AD与BE交点为F,则△ABF∽△BCA,由AB＝3,得AF＝,DF＝由DF为△BEC的中位线,则EC＝.

解题透视 如何求DF长,为什么DF是△BEC的中位线?由△ABD与△AED关于AD对称,观察知∠ADB＝∠ADE,DE＝DC;联想到外角 ∠BDE＝∠DEC＋∠DCE,可推出∠ADB＝∠DCE,得AD∥CE,中位线DF也就呼之欲出;转化为求AF,观察△ABF与△ABC相似,于是问题解决.

解后反思如何看出DF是三角形BEC的中位线?如何看出△ABF与△ABC相似的?

基于轴对称性,对应角、对应边相等(∠ADB＝∠ADE,DE＝DC),联想到外角性质,发现AD∥CE,进而发现DF为中位线;基于对称点连线BE被对称轴AD垂直平分,结合∠DAB＝∠DBA,构造出与“3,4,5”相似的Rt△.

1.3 解法三

解题思路 过A、D分别作AF⊥BC,DG⊥CE,则△ADF≌△DCG,DF＝CG,且DC＝,得DF＝

解题透视 如何想到作双高AF和DG的?根据轴对称性,观察知 ∠ADB＝∠ADE,DE＝DC,可推出∠ADB＝∠ECD,由角相等联想到相似,作高AF、DG(直角三角形斜边上的高AF,常见作法;等腰三角形DEC底边上的高DG,也是常见作法),构造相似三角形,事实上△ADF与△DCG全等,推出CE＝2DF,利用面积法求AF长,勾股定理求DF,解决问题.

解后反思 基于翻折特征,对应角相等,对应边相等,DE＝DC,∠ADF＝∠GCD,构造相似三角形(恰好全等);基于对“3,4,5”直角三角形的熟悉程度,作高AF,Rt△ADF三边已知,CD也已知,能求解CG.

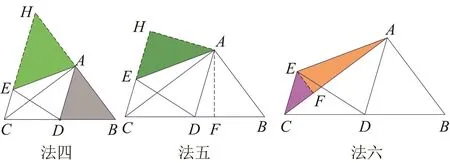
1.4 解法四

解题思路 延长BA、CE交于H,由于∠BCA＝ECA,所以CH＝CB＝5,△AEH∽

解题透视 为什么会想到延长BA、CE?如何快捷求出EH来?根据轴对称性,对应角相等、对应边相等,结合外角性质,得平行(AD∥CH),得角平分线(DC＝DA结合平行),结合∠BAC＝90°,构造等腰三角形;联想到AB＝AE＝AH,∠BAD＝ ∠H,构造相 似 △AEH,△DAB(三边已知)求解EH.

解后反思 基于翻折特征,对应角、边相等,由外角性质,才看出AD、CE平行,进而看出CA为角平分线,最后才联想到延长BA、CE.

1.5 解法五

解题思路 过A作AF⊥BC、AH⊥CE,△AEH∽△CBA∽△CAH,EH＝

解题透视 解法五与解法四有相同点,均发现CA为角平分线,不同点是解法五联想到角平分线的性质,作双高AF、AH,利用 △AEH∽△CHA∽△CAB,解决问题,比解法四更简洁.

解后反思 基于翻折特征,联想相关性质,推出CA为角平分线,由角平分线作垂线,构造“3,4,5”的直角三角形.

1.6 解法六

解题思路 过E作EF⊥AC,△CBA∽△CEF,设EF＝3x,CF＝4x,AF＝4－4x,在Rt△AEF中,32＝ 3x()2＋(4－4x)2,25x2－

解题透视 为什么过E点作AC的垂线EF?似乎感觉很唐突!由翻折特征,联想外角性质,推理出CA为角平分线,而∠ACB为“3,4,5”Rt△的已知角,自然 ∠ECF也为已知,作垂线,能构造“3,4,5”三角形,结合Rt△AEF,AE＝AB＝3,AC＝4,利用勾股定理解决问题,故作垂线EF不唐突,有道理!

解后反思 基于翻折特征,发现∠ECF＝∠ACB,构造3,4,5的直角三角形,利用勾股定理在Rt△AEF解决问题.

2 解法归纳和分析

翻折本质上就是轴对称,轴对称变换是初中数学重要的图形变换,历来是中考重点,但考生为什么普遍感觉难?先从它的特征说起.轴对称的性质有以下两条,若两个图形关于某直线轴对称,(1)则对应线段相等,对应角相等;(2)对应点连线被对称轴垂直平分;以上两点,学生无不理解,但问题就在于具体情景中,学生就显得无所适从.其中角相等的运用是难点.在上述六种解法中,经常出现基本图形(例如与“3,4,5”相似的三角形,直角三角形斜边上的高,角平分线等)这些图形是否熟悉,直接影响到学生的联想和思维发散.从角相等能联想到等腰三角形,联想到平行,联想到相似,学会联想很要紧;对应点连线被对称轴垂直平分其实能观察出Rt△,进而联想到相似三角形,勾股定理等.

3 对今后教学的建议

3.1 重视基本知识、基本性质,为分析问题、解决问题提供坚实的“物质基础”

数学基本概念、性质、法则、定理等是数学知识的核心,也是形成解题能力的基础,离开了基础知识的积累,解题能力就成为空中楼阁.轴对称是初中数学的重点和难点.它的性质学生掌握不全,知识结构混乱.轴对称实质是全等变换.对应边相等,对应角相等是它的首要特征;另外,对应点连线被对称轴垂直平分也是十分重要的性质,这一点学生往往忽视,教学时要强调对称轴的重要性.可以让学生从以下两个角度理解来牢固完整掌握轴对称的性质(1)它是全等变换;(2)对称轴的作用.解题能力的提高首先要十分熟悉相关性质和定理法则概念等.

3.2 重视积累基本图形,提高识图能力

基本图形是数学教学中长期总结出来的“珍珠”,具有强大生命力,经得起实践检验.它往往蕴涵着基本知识和基本方法.在复杂图形中若能发现或构造基本图形,就可以直接获取基本图形所蕴含的结论和方法,实现思维跳跃,大大降低思考力度.

上述解法中的基本图形有“3,4,5”的直角三角形;等腰三角形三线合一;Rt△斜边上的高;与“3,4,5”相似的Rt△;角平分线上的点到角两边的距离相等.这些图形和基本特征的积累,有助于提高学生的识图能力,有助于打开学生解题的思路,发散学生的思维,提高解题能力.

3.3 重视对学生联想能力的培养,提高学生的发散思维

联想解题就是从题目已知条件展开发散,想象,从自己知识仓库中找出与题目条件接近或相似的结论或基本图形或定理,变通使用这些知识,从而解决问题.基础知识和基本图形就是“珍珠”,有了珍珠还必须用线串起来才精彩,这根线就是联想.例如看到等腰三角形就能联想到三线合一,已知直角三角形两边求斜边上的高就能联想到面积法,看到角平分线就能联想到角平分线的性质,能识别出角相等就能联想到构造相似三角形(往往是Rt△).这些联想要在平时教学中潜移默化的渗透,不断“厚积”,方能“薄发”.

注：“3,4,5”的直角三角形是指与边长为“3,4,5”的直角三角形相似的三角形.

2017-09-05)