对一道压轴选择题错误解答的探析

安徽师范大学附属中学高三年级部 殷 畅 李 正 (邮编：241001)

对一道压轴选择题错误解答的探析

安徽师范大学附属中学高三年级部 殷 畅 李 正 (邮编：241001)

长沙市2017届高三年级上学期统一模拟测试理科第12题：对于满足0＜b≤3a的任意实数a、b,函数fx()＝ax2＋bx＋c总有两个不同的零点,则的取值范围是( )

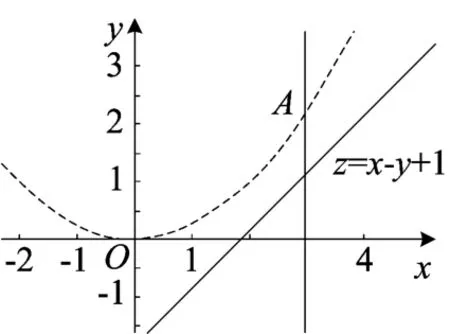
图1

最初的解法 依题意对于任意的满足0＜b≤3a的实数a、b,有 △＝b2－4ac＞0,题目就变成了“已知的取值范围”.于是就想到了转化为线性规划：已知的取值范围.很兴奋!剩下只需要换元,将、的取值范围.如图1所示,当1＋x－y到点A(3,时取到最小,所以范围是,但是发现没有答案.

再认真检查解答,发现了问题之所在——题目的条件“实数a、b的任意性”没有考虑.那就应该是相切时最小.如图2所示,求出切点为B(2,1),故而范围是 (2 ,＋∞).答案对了.

这种解法是将三元消为二元,并利用到线性规划这个看似与本题无干的知识点解决问题,有点激动!

但是再仔细揣摩一下,却觉得解答还是有点问题.“实数a、b的任意性”只是控制 △ ＝b2－4ac＞0的,对目标函数是没有这个要求的.所以答案应该还是不对!

图2

原答案解析 依题意对于任意的满足0＜b≤3a的实数a、b,有△＝b2－4ac＞0,于是c＜,对于任意的满足0＜b≤3a的实数a、b恒成立.令t＝,因为0＜b≤3a,故0＜t≤3.因此1＋t－t2∈ (1,2],所以2,选D.

应该说,题目设计巧妙,由函数到不等式再到函数,的确不易想到.但是提供的解答同样也是有问题的!

依题意对于任意的满足0＜b≤3a的实数a、b,有 △＝b2－4ac＞0,于是c＜,此时就应该得到c的范围.不存在“从而,对于任意的满足0＜b≤3a的实数a、b恒成立.”也就是说,恒成立仅仅是“对于任意的满足0＜b≤3a的实数的范围.故而解答是错误的.

与老师一同分析,最后得到的正确解答应该是：任意的满足0＜b≤3a的实数a、b,于是c.先求出c的范围：由于是恒成立,故c＜而在选项中就没有这个答案了.

通过整个解题过程的探索加深了对“任意性”的理解.

解题反思 波利亚在《怎样解题》中指出：“碰上一个不完整的念头怎么办?应该加以考虑.如果它看来有好处,就应该多考虑一会儿.如果它看来是可靠的,你应当确定它能引导你走多远,并重新考虑一下形势.由于这个有益的念头,情况已经变化了.你要从各个方面来考虑新形势并找出它与你现有知识之间的联系.”笔者一开始的解答应该是非常“有益”的念头,只是思考不够完备.但是由于有了这个“有益的念头”,题目解答的真相其实已经不远.线性规划的解法结合数形结合,似乎比答案的“放缩”更容易接受,也更容易理解.

题目反思 宋玉在《登徒子好色赋》所描述：东家之子,增之一分则太长,减之一分则太短;著粉则太白,施朱则太赤.笔者的解答与原答案正好一个是不足,一个是过了.回想这个题目,既然没有选项了,应该是有缺憾的,不能称为“东家之子”了.编题者原本用意定是希望学生按照所提供的解答的路子,那么我们也可以认为原题目表达是不足的.

按解答思路,原题可以修改为：已知0＜b≤3a,函数fx()＝ax2＋bx＋c总有两个不同的零点,若对任意满足条件的实数a、b,m＝

总有意义,则实数m的取值范围是( )

,

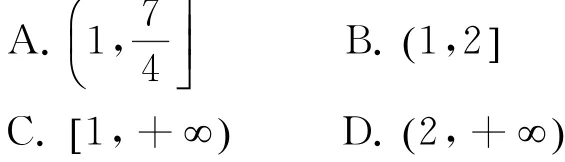
2017-09-20)