多角度探究求目标函数的最值题型

■河北省邢台市第十九中学 刘鹏杰

多角度探究求目标函数的最值题型

■河北省邢台市第十九中学 刘鹏杰

线性规划问题是高考的重点,并且线性规划问题具有代数和几何的双重形式,多与函数、平面向量、数列、三角、概率等问题交叉渗透,自然地融合在一起,使数学问题的解答变得更加新颖别致。归纳起来常见的命题角度有:(1)求线性目标函数的最值;(2)求非线性目标的最值;(3)求线性规划问题中的参数值。

求目标函数的最值要明确以下几个概念:

(1)约束条件:由变量x,y组成的不等式(组);

(2)线性约束条件:由关于x,y的一次不等式组成的不等式组;

(3)目标函数:关于x,y的函数解析式,如z=2x+3y等;

(4)可行解:满足线性约束条件的解(x,y);

(5)最优解:使目标函数取得最大值或最小值的可行解。

题型一：求线性目标函数的最值

A.10 B.8 C.3 D.2

解析：作出可行域,如图1中阴影部分所示。

由z=2x-y得y=2x-z,作出直线y=2x,平移使之经过可行域,观察可知,当直线经过点A(5,2)时,对应的z值最大。故zmax=2×5-2=8。选B。

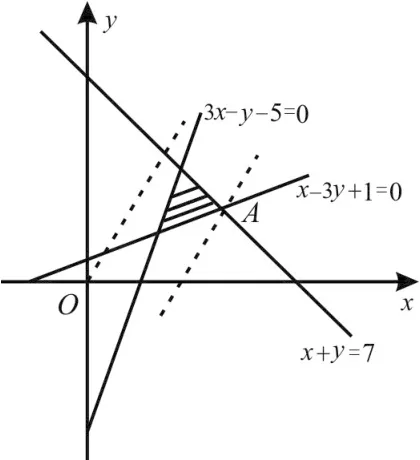
图1

解析：根据题意画出可行域,如图2所示。

图2

题型二：求非线性目标的最值

解析：不等式组表示的平面区域如图3中阴影所示,显然当点M与点A重合时直线OM的斜率最小。由直线方程x+2y-1=0和3x+y-8=0,解得A(3,-1),故OM斜率的最小值为设实数x,y满足不等式组则x2+y2的取值范围是( )。

图3

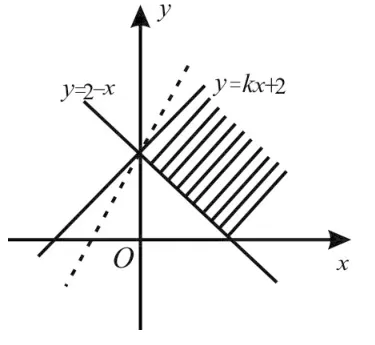
图5

图6

A.[1,2]

B.[1,4]

C.[2,2]

D.[2,4]

解析：如图4所示,不等式组表示的平面区域是△ABC的内部(含边界),x2+y2表示的是此区域内的点(x,y)到原点距离的平方。从图中可知最短距离为原点到直线BC的距离,其值为1;最远的距离为AO,其值为2。故x2+y2的取值范围是[1,4]。选B。

图4

题型三：求线性规划中的参数

当k＜-1时,z=y-x取得最小值2,当k=-1时,z=y-x取得最小值-2,均不符合题意。

当-1＜k＜0时,如图6所示,此时可行域为点A(2,0),B(-2,0),C(0,2)所围成k的三角形区域,当直线z=y-x经过点时有最小值,即-选D。已知x,y满足约束条件若z=y-ax取得最大值的最优解不唯一,则实数a的值为( )。

C.2或1 D.2或-1

解法1：由题中条件画出可行域,如图7中阴影部分所示。可知A(0,2),B(2,0),C(-2,-2),则zA=2,zB=-2a,zC=2a-2,要使目标函数取得最大值的最优解不唯一,只要zA=zB＞zC或zA=zC＞zB或zB=zC＞zA,解得a=-1或a=2。选D。

图7

解法2：目标函数z=y-ax可化为y=ax+z,令l0:y=ax,平移l0,则当l0∥AB或l0∥AC时符合题意,故a=-1或a=2。选D。

方法与思路归纳:

1.求目标函数的最值的一般步骤为:一画,二移,三求,关键是准确作出可行域,理解目标函数的意义。

2.常见的目标函数有:

(1)截距型:形如z=ax+by,求这类目标函数的最值常将函数z=ax+by转化为直线的斜截式:通过求直线的截距的最值间接求出z的最值。

(2)距离型:形如z=(x-a)2+(y-b)2。

(责任编辑 徐利杰)