必修五综合测试（B卷）答案与提示

2017-12-16 03:33:51

中学生数理化(高中版.高二数学) 2017年11期

必修五综合测试（B卷）答案与提示

一、选择题

1.A 2.C 3.D 4.C 5.B 6.B 7.D 8.D 9.C 10.B 11.C 12.D 13.B 14.D 15.C 16.B 17.C 18.D 19.C 20.C 21.A 22.B 23.B 24.A 25.D 26.B 27.D 28.B 29.C 30.B 31.C 32.C 33.D 34.C 35.B 36.C 37.C 38.C 39.A

二、填空题

三、解答题

58.(1)依题意,可知方程ax2+3x-1=0的两个实数根为解得a=-2。

(2)-2x2-3x+5＞0,即2x2+3x-5＜0。因为2x2+3x-5=0有两根为x1=1,,所以不等式的解集为

59.(1)f(x)＞k,即kx2-2x+6k＜0,由已知其解集为{x|x＜-3或x＞-2},得x1=-3,x2=-2是方程kx2-2x+6k=0的两根。

由已知fx()≤t对任意x＞0恒成立,故实数t的取值范围是

60.(1)因为b2=ac,且a2-c2=ac-bc,所以b2+c2-a2=bc。

在△ABC中,由余弦定理得:

因为b2=ac,A=60°,所以

61.(1)在△ABC中,因为3a=2b,所以3sinA=2sinB。

又因为B=60°,所以代入得3sinA=2sin60°,解得sin

由于数列{an}是正项数列,所以Sn＞0,Sn=n2+n。

于是a1=S1=2。

当n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n。

综上可知,数列{an}的通项an=2n。

63.(1)a1=2,a2=2+c,a3=2+3c。

因为a1,a2,a3成等比数列,所以(2+c)2=2(2+3c),解得c=0或c=2。

因为c≠0,所以c=2。

(2)当n≥2时,由于a2-a1=c,a3-a2=2c,…,an-an-1=(n-1)c,则:

an-a1=[1+2+…+(n-1)]c=

又a1=2,c=2,故有an=2+n(n-1)=n2-n+2(n=2,3,…)。

当n=1时,上式也成立。

故an=n2-n+2(n=1,2,3,…)。

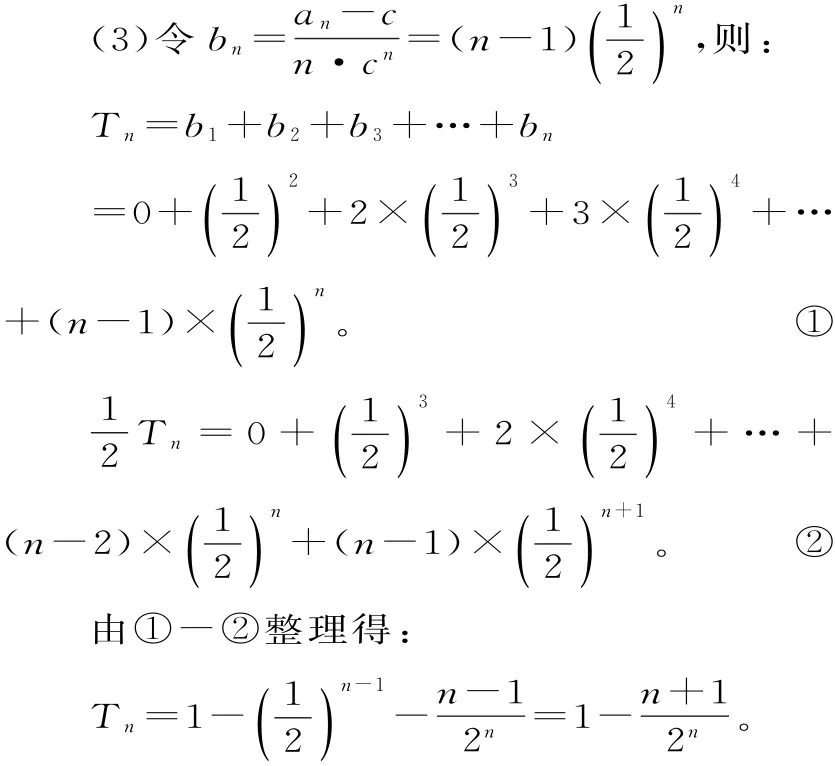
(责任编辑徐利杰)