例谈竞赛中的数列题型及其方法

■广东省兴宁市第一中学 蓝云波

例谈竞赛中的数列题型及其方法

■广东省兴宁市第一中学 蓝云波

数列在竞赛中的考点多,考查频率高,命题设置灵活,是考查同学们综合素质与能力的极好的素材。为了帮助同学们更好地备战高中数学联赛,下面通过对近几年各地竞赛题的分类例析,以帮助同学们提高学习效率。

一、知识点梳理

数列竞赛题对代数变形能力要求较高,下面是一些重要的代数变形技巧。

1.常见的裂项技巧。

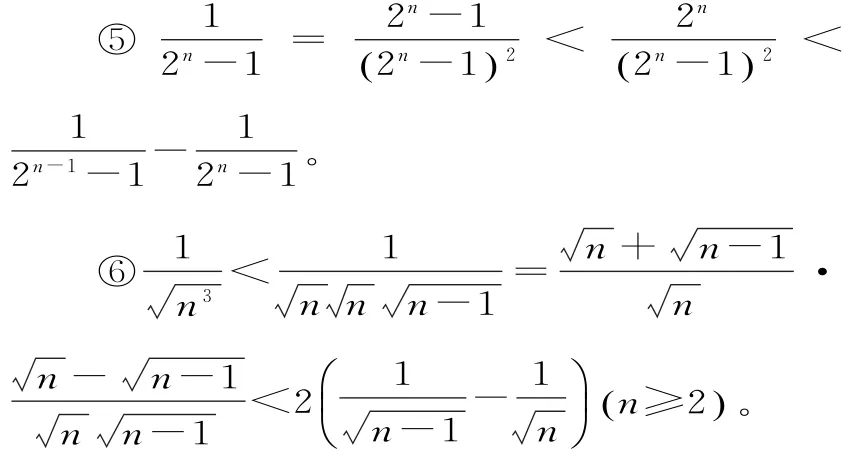
二、题型例析

题型一 等差数列的基本概念和性质

解析：设等差数列an{}的公差为d,则由题设可得a1+nd+a1+(n-1)d=2dn+2a1-d=4n-58。因为此式恒成立,所以2d=4,且2a1-d=-58。解得d=2,a1=-28。所以a2015=a1+2014d=4000。

点评:等差数列的公差与首项的求解,常常要借助方程(组)的思想,同时对运算求解能力有一定的要求。

解析：(解法1)设{an}和{bn}的公差分别为d1,d2,则由

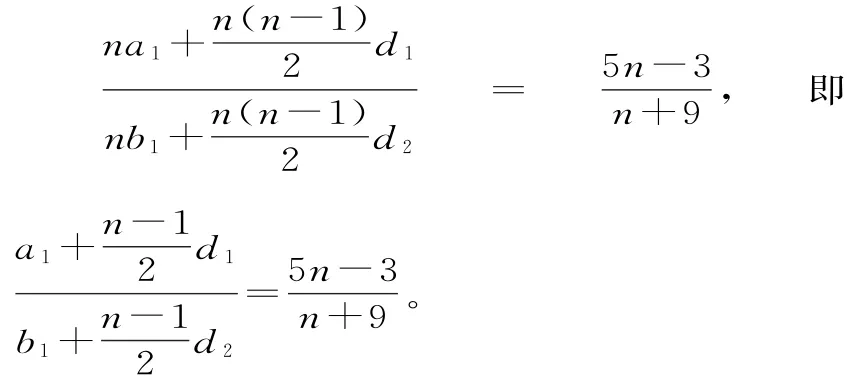
设d2=d,则d1=5d,进一步可得到a1=d,b1=5d。于是有

点评:等差数列问题中,等差数列的性质的合理运用是灵活解题的关键。解法1比较直接,但运算量较大;而解法2通过利用等差中项的性质,实现了问题的快速解决。

题型二 等比数列的基本概念和性质

点评:本题是一个隐蔽的等比数列问题,在通过赋值得到an{ }是一个等比数列后,问题便迎刃而解。

题型三 等差数列与等比数列的综合

因为d＞0,所以a1=d,于是an=nd,从而bn=a2n=d·2n。

点评:本题综合考查了等差数列与等比数列的基础知识,对基本概念、公式的理解是解题的关键。

题型四 倒序求和法

点评:这是一道极为经典的倒序求和问题,这类试题往往给出一个优美的函数,然后借助该函数蕴含的一个奇妙性质进行求和,而这个蕴含的奇妙性质,往往需要对所需求和的式子进行观察而获得。

题型五 并项求和法

A.-2016 B.-1008

C.2016 D.4032

解析：因为an+an+1=(-1)n(2n-1)+(-1)n+1(2n+1)=(-1)n[(2n-1)-(2n+1)]=(-1)n+1·2,所以当n为奇数时,an+an+1=2。

故数列an{}的前2016项之和S2016=(a1+a2)+(a3+a4)+…+(a2015+a2016)=2×1008=2016,故选C。

点评:对于通项公式含有(-1)n的数列求和问题,通常可采取并项求和的策略求和,通过并项,转化为常规的数列求和问题。

题型六 裂项求和法

点评:裂项求和方法源于课本习题,是高考中考查频率最高的求和方法,有多种不同形式,具有较强的灵活性,对代数变形能力的要求很高。

点评:本题是三角形式的裂项求和问题,令人耳目一新。

题型七 错位相减求和法

(1)求数列{an}的通项公式;

(2)令bn=anlog3an,求数列{bn}的前n项和Tn。

两式相减,得an+1=c·an(n≥2),又知所以数列{an}是公比为c的等比数列。

(2)因为bn=3n-1log33n-1=(n-1)3n-1,所以Tn=1·3+2·32+3·33+…+(n-1)·3n-1。

故3Tn=1·32+2·33+3·34+…+(n-1)·3n。

点评:错位相减法源于等比数列的求和公式的推导过程。在高考中,常考查差比型的数列求和问题(差比型数列即数列的通项公式的形式为等差数列乘以等比数列)。这种方法具有一定的运算量,解题的关键是对差比型数列的识别和运算能力。

题型八 数列型不等式

(1)求数列{an}的通项公式;

(2)令bn=,n∈N*,Sn是数列{bn}的前n项和,求证:Sn＜1。

又a1=3f(1)-f(0)=8,所以数列{an}是首项为8,公比为3的等比数列。

所以an=8·3n-1。

(2)因为bn=所以当n≥2时,

综上知命题得证。

点评:数列不等式是竞赛中的重点,对大部分数列和型不等式问题,不能直接求和,但在通过放缩后,却能进行求和。

(责任编辑 徐利杰)