具有非线性脉冲效应和反应扩散项的Cohen-Grossberg型模糊神经网络的指数同步

蒲 浩， 黄建文， 赵爱亮， 刘衍民

(1. 遵义师范学院 数学学院, 贵州 遵义 563006; 2. 西南大学 数学与统计学院, 重庆 400715)

具有非线性脉冲效应和反应扩散项的Cohen-Grossberg型模糊神经网络的指数同步

蒲 浩1， 黄建文2， 赵爱亮1， 刘衍民1

(1. 遵义师范学院 数学学院, 贵州 遵义 563006; 2. 西南大学 数学与统计学院, 重庆 400715)

研究了具有非线性脉冲效应和反应扩散项的Cohen-Grossberg型模糊神经网络的指数同步,通过Lyapunov稳定性理论和不等式技巧,利用p-范数得到了新的指数同步的充分条件.

模糊神经网络; 非线性脉冲效应; Cohen-Grossberg型神经网络; 反应扩散项; 混合时滞;p-范数

自从1983年M. A. Cohen和S. Grossberg[1]首次提出Cohen-Grossberg型神经网络模型以来,引起了许多学者对Cohen-Grossberg型神经网络模型同步的广泛研究,得到了很多有用的不同类型的神经网络模型同步的理论[2-6].这些理论不仅在很多理论研究中有着重要应用,而且还被广泛的应用到生产实践中.例如,联想记忆、安全通信和人工智能系统.

对于自然界中的一个实际的神经网络,要实现信号传递的同步,不可避免的受到来自系统自身因素和外界因素的影响,比如信号在不同的神经元之间的传递过程中,由于信号传递的速度是有限的,从而引起信号在不同神经元之间传递过程中有滞后现象出现[7];由于电子在一个非均匀的电磁场运动时,不可避免的在神经网络中会出现扩散现象[8-9];信号在不同的神经元之间传递时,不可避免的要受到外界的干扰,出现信号的短暂振动现象[10].

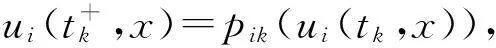
1 模型和预备知识

考虑如下的具有非线性脉冲效应和反应扩散项的Cohen-Grossberg型模糊神经网络模型

(1)

其中i∈I={1,2,…,n},Z+={1,2,…};x=(x1,x2,…,xm)T∈Ω⊂Rm,Ω={(x1,x2,…,xm)T||xl|lt;ll,l∈M={1,2,…,m}}在空间Rm上是一个有光滑边界Ω的有界紧集且mesΩgt;0;∧和∨分别表示模糊“与”,模糊“或”算子;Ii表示对第i个神经元的偏斜输入量;fj(·)和gj(·)分别表示在t时刻对空间位置x处的第j个神经原的激活函数;ui(t,x)表示第i个神经元在t时刻和空间位置x处的状态变量;0≤τj(t)≤τj表示t时刻不同的神经元之间信号的转换时滞,σjgt;0表示对第j个神经元的离散扰动时滞;bij、cij、ωij都是常数且常数qilgt;0,τj≤σj,j∈I;脉冲时刻tk∈{tk|0≤tk-1lt;tk,k∈Z+}且

和

pik(u)=pik(u1,u2,…,un)∈[Rn,R]

表示tk时刻第i个单元的非线性脉冲扰动函数.

对应于系统(1)的初值条件为

ui(s,x)=φi(s,x),

(s,x)∈[-r,0]×Ω,i∈I,

ui(t,x)=0,

(t,x)∈[-r,+∞)×∂Ω,i∈I,

(2)

其中

φ(s,x)=(φ1(s,x),φ2(s,x),…,φn(s,x))T∈

C=([-r,0]×Ω,Rn)

指的是把[-r,0]×Ω映射到Rn上的所有连续函数，组成的一个具有p-范数的Banach空间(p≥1是一个正整数),其中p-范数在本文中定义形式为

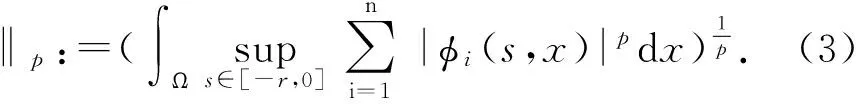
对于系统(1),假设:

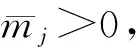
|fj(vj)-fj(uj)|≤Lj|vj-uj|,

|gj(vj)-gj(uj)|≤Nj|vj-uj|,

对任意的uj,vj∈R,j∈I成立;

(H2) 对任意i∈I,存在一个常数γigt;0,使得

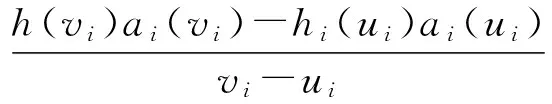
(4)

对任意的ui,vi∈R且ui≠vi成立;

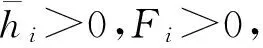
|hi(vi)-hi(ui)|≤Fi|vi-ui|

对任意的i∈I,ui,vi∈R成立.

把系统(1)作为主驱动系统.为了同步,引入如下的响应系统

(5)

其中Ki(t)表示的是如下的外部输入控制

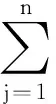
(6)

每一个kij(i∈I)是一个常数叫做控制收益.

响应系统(5)的初值条件是

vi(s,x)=φi(s,x),
(s,x)∈[-r,0]×Ω,i∈I,
vi(t,x)=0,
(t,x)∈[-r,+∞)×∂Ω,i∈I,

其中

φ(s,x)=(φ1(s,x),φ2(s,x),…,φn(s,x))T∈

C([-r,0]×Ω,Rn).

定义同步误差为

ei(t,x)=vi(t,x)-ui(t,x),i∈I.

由系统(1)和(5),可以得到如下误差系统

(7)

定义1如果存在常数M≥1使得

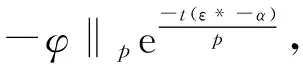
(8)

就称驱动系统(1)和响应系统(5)是全局指数同步的,其中范数定义为

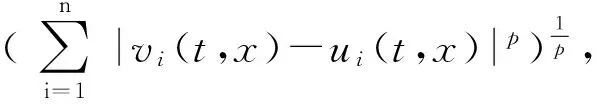
和

v(t,x)=(v1(t,x),v2(t,x),…,vn(t,x))T

是驱动系统(1)和响应系统(5)满足初值条件φ,φ∈C([-r,0]×Ω,Rn)的解.

2 几个引理

引理1[14]假设ui、vi是系统(1)和(5)中的2个状态变量，则有

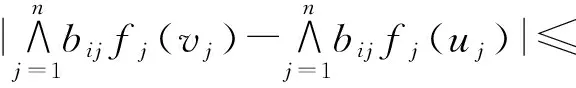
对任意的bij、cij及i,j∈I成立.

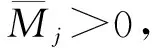
对任意的uj∈R,j∈I成立.

记

(9)

则下式成立:

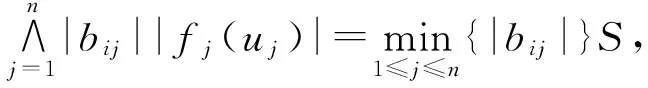
(10)

为了方便,记

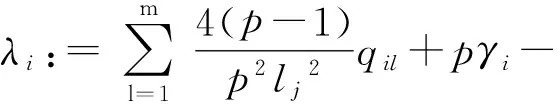
(11)

(13)

(14)

(H5) 假设λi-αi-βi-digt;0对任意的i∈I成立.

为了证明结论,构造一个以εi为变量的一元函数

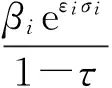
由假设(H5)知Fi(0)gt;0.

因此,关于εi的方程

λi-αi-βieεiσi-dieεiσi-εi=0,i∈I

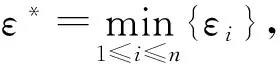
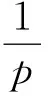
由引理2知,不等式

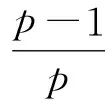
(15)

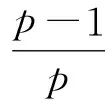
(16)

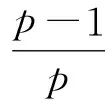
(17)

成立.

引理3[16]若p≥2是一个正整数,ll(l∈M)是一个正常数,Ω={(x1,…,xm)T||xl|lt;ll,l∈M},d(x)是一个实值函数且d(x)∈C1(Ω),同时d(x)|∂Ω=0,则有

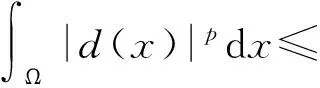
为了后面证明结论的需要，结合边界条件(2)和引理3,有如下式子成立:

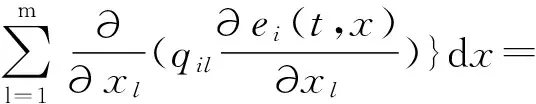
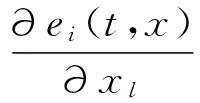
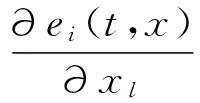
x.(18)

为了得到文章的主要结论,给出下面几个假设

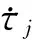
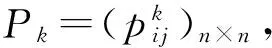
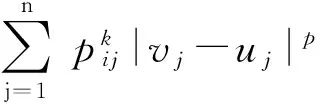
对任意的(u1,u2,…,un)∈Rn,(v1,v2,…,vn)∈Rn,i∈I和k∈Z+成立.

(H8) 存在一个常数α≥0使得

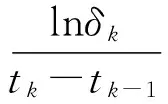
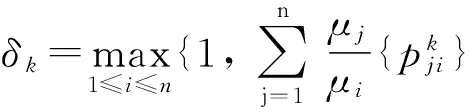
3 主要结果

定理1如果(H1)～(H8)都成立,则驱动系统(1)和响应系统(5)是全局指数同步的.

证明构造如下形式的Lyapunov函数

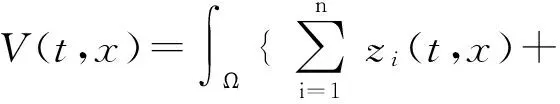
(19)

其中

zi(t,x)=μieε*t|ei(t,x)|p,i=1,2,…,n.

当t≠tk时,结合(7)式，利用引理1～3所得的结论(9)～(18)及假设(H1)～(H6),对V(t,x)关于t计算Dini右上导数,可以得到下面的式子

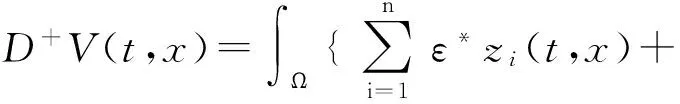
|ej(t-τj(t),x)||ei(t,x)|p-1+

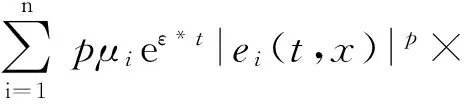
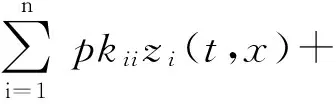
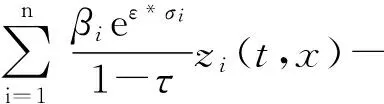
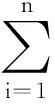
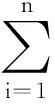
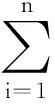
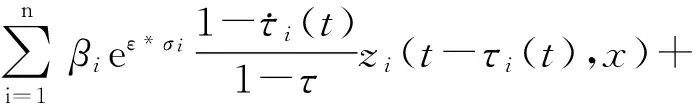
(20)

定义

(21)

根据(19)和(20)式有

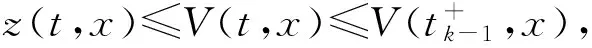
(22)

根据(19)和假设(H7),对k∈Z+,

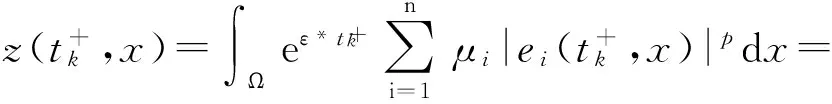
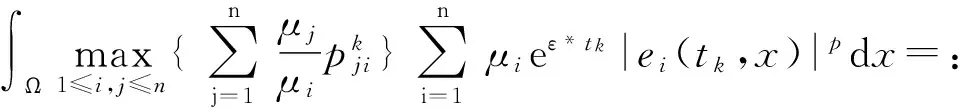
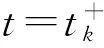
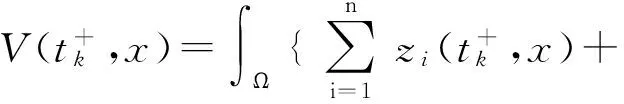
(24)

由(22)和(23)式有

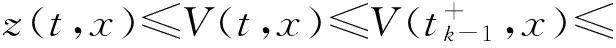
(25)

对任意的t∈(tk-1,tk],k∈Z+,其中δ0=1.由假设(H8)可知，δk≤eα(tk-tk-1),k∈Z+.

由上式可得下列结果

z(t,x)≤eα(t1-t0)eα(t2-t1)…×

eα(tk-1-tk-2)V(0,x)≤eαtV(0,x)

对任意的t∈(tk-1,tk],k∈Z+成立.

当t=0时,

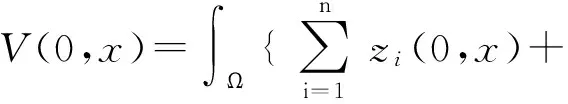
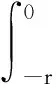
(26)

由(25)式可得

z(t,x)≤eαtV(0,x),

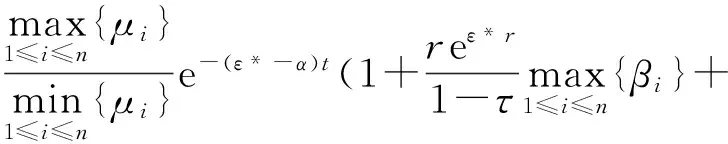
(27)

从而

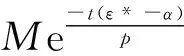
(28)

其中

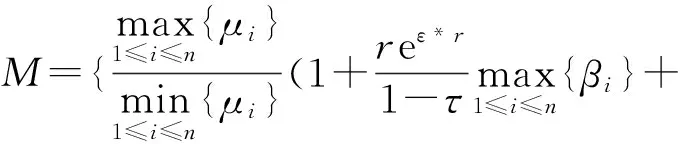
说明系统(1)和系统(5)是指数同步的.

4 推论

推论1如果假设(H1)～(H4)及(H6)都成立,同时

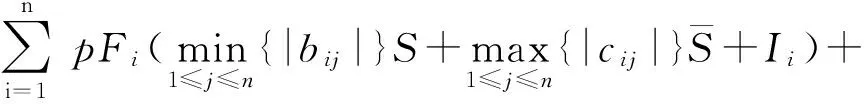
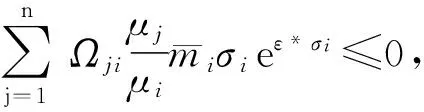
则驱动系统(1)和响应系统(5)是全局指数同步的.

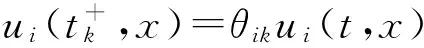
如果在驱动系统(1)和响应系统(5)中反应扩散项中的qil=0时,根据本文中的定理1,有下列结论成立.

推论2如果(H1)～(H4)及(H6)～(H8)成立,同时

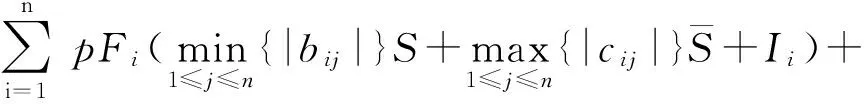
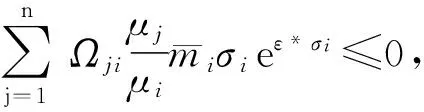
则驱动系统(1)和响应系统(5)是全局指数同步的.

注2当有式子

时,

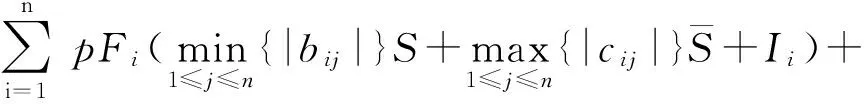
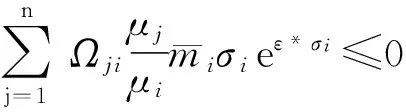
更容易成立,通过此式可以发现一个有趣的现象,神经网络中有反应扩散项比没有反应扩散项容易实现同步.

[1] COHEN M A, GROSSBERG S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks[J]. IEEE Trans Syst, Man and Cybernetics,1983,13(5):815-826.

[2] YU J, HU C, JIANG H J, et al. Exponential synchronization of Cohen-Grossberg neural networks via periodically intermittent control[J]. Neurocomputing,2011,74(10):1776-1782.

[3] YANG X S, CAO J D, YU W W. Exponential synchronization of memristive Cohen-Grossberg neural networks with mixed delays[J]. Cognitive Neurodynamics,2014,8(3):239-249.

[4] GAN Q T. Exponential synchronization of stochastic Cohen-Grossberg neural networks with mixed time-varying delays and reaction-diffusion via periodically intermittent control[J]. Neural Networks,2012,31:12-21.

[5] CHEN Z, YANG H. Complete synchronization for impulsive Cohen-Grossberg neural networks with delay under noise perturbation[J]. Chaos, Solitions amp; Fractals,2009,42(3):1664-1669.

[6] LI T, SONG A G, FEI S M. Synchronization control for arrys of coupled discrete-time delayed Cohen-Grossberg neural networks[J]. Neurocomputing,2010,74(1):197-204.

[7] YAN P, LYU T. Exponential synchronization of fuzzy cellular neural networks with mixed delayed and general boundary conditions[J]. Commum Nonlinear Sci Numer Simulat,2012,17(2):1003-1011.

[8] LI J M, ZHANG W Y, CHEN M L. Synchroization of delay reaction-diffusion neural networks via an adaptive learing control approach[J]. Comput Math Appl,2013,65(11):1775-1785.

[9] JING K. Exponential stability of FCNNs with time-varying leakage delays and reaction-diffusion terms[J]. Neurocomputing,2014,145(12):363-368.

[10] LONG S J, SONG Q K, WANG X H, et al. Stability analysis of fuzzy cellular neural networks with time delay in the leakage term and impulsive perturbations[J]. J Franklin Inst,2012,349(7):2461-2479.

[11] FENG X M, ZHANG F Q, WANG W J. Global exponential synchronization of delayed fuzzy cellular neural networks with impulsive effects[J]. Chaos, Solitons Fractals,2011,44(1/2/3):9-16.

[12] DING W. Synchronization of delayed fuzzy cellular neural networks with impulsive effects[J]. Commun Nolinear Sci Numer Simulat,2009,14(11):3945-3952.

[13] SHENG L, YANG H Z. Exponential synchronization of a class of neural networks with mixed time-varying delays and impulsive effects[J]. Neurocomputing,2008,71(16/17/18):3666-3674.

[14] YU J, HU C, JIANG H J, et al. Exponential lag synchronization for delayed fuzzy cellular neural networks via periodically intermittent control[J]. Math Comput Simul,2012,82(5):895-908.

[15] GAN Q T. Exponential synchronization of stochastic fuzzy cellular neural networks with reaction-diffusion terms via periodically intermittent control[J]. Neural Process Lett,2013,37(3):393-410.

[16] HU C, YU J, JIANG H J, et al. Exponential synchronization for reaction-diffusion networks with mixed delays in terms ofp-norm via intermittent driving[J]. Neural Networks,2012,31(12):1-11.

2010MSC:82C32

(编辑 周 俊)

Exponential Synchronization for Cohen-Grossberg Fuzzy Neural Networks with Nonlinear Impulsive Effects and Reaction-Diffusion Terms

PU Hao1, HUANG Jianwen2, ZHAO Ailiang1, LIU Yanmin1

(1.SchoolofMathematics,ZunyiNormalCollege,Zunyi563006,Guizhou;2.SchoolofMathematicsandStatistics,SouthwestUniversity,Chongqing400715)

In this paper, we study the exponential synchronization for Cohen-Grossberg fuzzy neural networks with nonlinear impulsive effects and reaction-diffusion terms. By the Lyapunov functinoal method and some inequality techniques, some new and useful sufficient conditions on the exponential synchronization are obtained from ap-norm.

fuzzy neural networks; nonlinear impulsive effect; Cohen-Grossberg neural networks; reaction-diffusion terms; mixed delays;p-norm

O175.1

A

1001-8395(2017)06-0772-08

10.3969/j.issn.1001-8395.2017.06.011

2016-04-01

国家自然科学基金(71461027)和贵州省科技计划课题(黔科合LH字[2015]7053号、[2015]7001号和[2015]7007号)

蒲 浩(1986—),男,讲师,主要从事神经网络和复杂网络同步的研究,E-mail:puhao2100@163.com