结构元线性生成的模糊值函数极限的新定义与性质

舒天军, 莫智文

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

结构元线性生成的模糊值函数极限的新定义与性质

舒天军, 莫智文*

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

用一种模糊距离给出结构元线性生成的模糊值函数极限的一种新定义,然后应用这种极限定义证明结构元线性生成的模糊值函数极限的加法与数乘运算、局部有界性、唯一性、局部保号性、保不等式性和迫敛性的6个性质定理,最后给出一个判断结构元线性生成的模糊值函数极限存在的柯西准则定理.

模糊距离; 结构元; 模糊值函数; 极限

自从L. A. Zadeh于1965年提出模糊集合理论以来,经过50多年的发展,模糊系统理论及其应用成果显著,且不断完善,其中关于模糊值函数极限的定义,一些学者做了研究[1-15],其理论依据是扩张原理.对于模糊值函数的一个分支,结构元线性生成的模糊值函数的概念由郭嗣琮[16]提出.文献[10]根据结构元线性生成的模糊值函数的表达式,给出了结构元线性生成的模糊值函数极限的一种定义.本文将利用文献[11]给出的模糊距离,结合模糊集的分解定理得出一种新的方法定义结构元线性生成的模糊值函数的极限,然后对结构元线性生成的模糊值函数极限的相关性质进行研究,并给出一个结构元线性生成的模糊值函数极限存在的充要条件.

1 预备知识

定义1.1[9]E是实数域R上的模糊集,隶属函数记为E(x),x∈R.如果E(x)满足下述性质：

1)E(0)=1,E(1+0)=E(-1-0)=0;

2) 在区间[-1,0)和(0,1]上,E(x)分别是单调增右连续函数和单调降左连续函数;

3) 在区间(-∞,-1)或(1,+∞)上,E(x)=0,则称模糊集E为R上的模糊结构元.

显然,模糊结构元E是R上的正则凸模糊集,是有界闭模糊集.

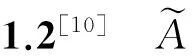
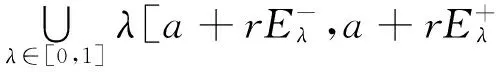
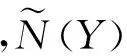
h(x)+ω(x)E,∀x∈D,ω(x)gt;0}.

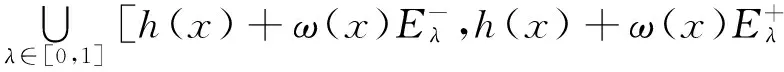
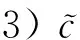
2 N(Ef)中模糊值函数极限的新定义和性质

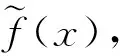
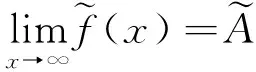
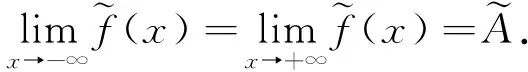
由定义2.1容易证明.

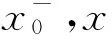
由定义2.2和定理2.1不难推出定理2.2.

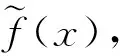
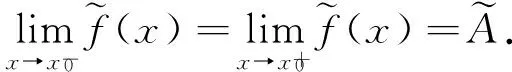
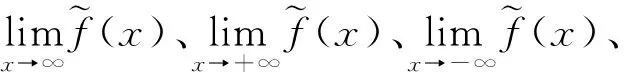
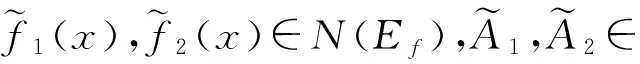
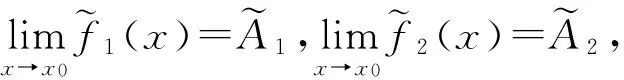
当0lt;|x-x0|lt;δ2时有

令δ=min{δ′,δ1,δ2},则当0lt;|x-x0|lt;δ时有

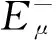
即证

2) 类似于证明1).

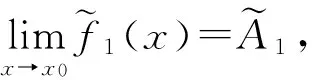
令δ=min{δ′,δ1},则当0lt;|x-x0|lt;δ时有

所以

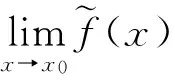
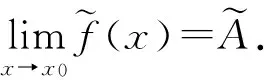
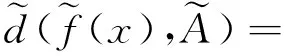
则

且

可以推出

且

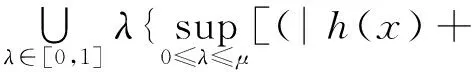
则有

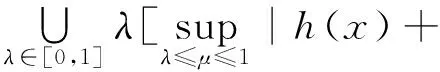
且

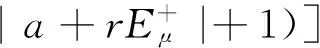
所以

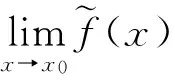
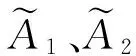
当0lt;|x-x0|lt;δ2时有

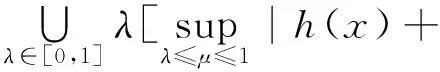
令δ=min{δ1,δ2},则当0lt;|x-x0|lt;δ时有

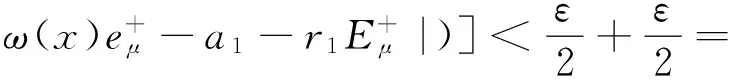
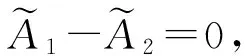
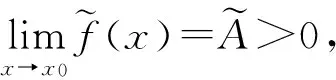
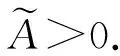
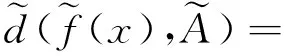
则

且

有

且

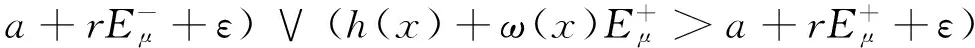
所以

即证.

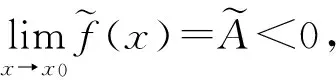
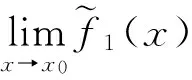
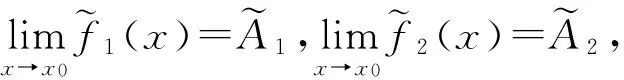
则有

且

从而

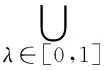
当0lt;|x-x0|lt;δ2时有

则有

且

从而

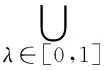
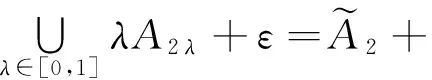
令δ=min{δ′,δ1,δ2},则当0lt;|x-x0|lt;δ时有

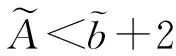
由ε的任意性可推出A≤B,即证

).

定理2.8(迫敛性) 若

且在x0的某空心邻域U0(x0)内有

则

证明因为

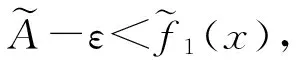
ε.

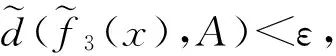
3 N(Ef)中模糊值函数极限的存在条件

证明必要性 设

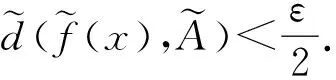
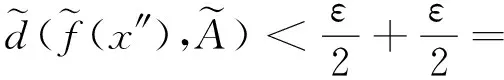
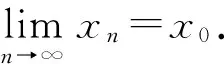
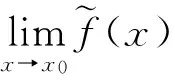
[1] ZHANG G. Fuzzy continuous function and it’s properties[J]. Fuzzy Sets and Systems,1991,43(2):159-171.

[2] BURGIN M. Theory of fuzzy limits[J]. Fuzzy Sets and Systems,2000,115(3):433-443.

[3] BURGIN M. Neoclassical analysis:fuzzy continuity and convergence[J]. Fuzzy Sets and Systems,1995,75(3):291-299.

[4] 刘宇. 区间值函数与模糊值函数的极限[J]. 东北师大学报(自然科学版),1994,26(3):19-23.

[5] 毕淑娟,吴从炘. 模糊数的运算性质及模糊数的距离与极限[J]. 模糊系统与数学,2000,14(3):40-44.

[6] 张广全. Fuzzy数的Fuzzy距离与Fuzzy极限[J]. 模糊系统与数学,1992,6(2):21-28.

[7] 郭嗣琮. 模糊值函数极限与连续的模糊结构元表示[J]. 海南师范大学学报(自然科学版),2008,21(4):351-356.

[8] 郭兴梅,张慧. 模糊值函数的极限与性质[J]. 滁州学院学报,2013,15(5):21-23.

[9] 郭嗣琮. 模糊值函数分析学的结构元方法(I)[J]. 辽宁工程技术大学学报,2002,21(5):670-674.

[10] 李安国,金红伟,张志宏,等. 模糊极限的一种新定义[J]. 辽宁工程技术大学学报,2004,23(6):845-847.

[11] 郭嗣琮. 基于结构元理论的模糊数学分析原理[M]. 沈阳:东北大学出版社,2004:97-113.

[12] 殷凤,王鹏飞. 模糊值函数极限(连续)及导数的新定义[J]. 中北大学学报(自然科学版),2011,32(6):662-666.

[13] 刘浪. 论模糊数的模糊距离[J]. 湘潭师范学院学报(自然科学版),2006,28(1):5-7.

[14] 刘慧林,冯汝鹏. 新的模糊数的模糊距离[J]. 模糊系统与数学,2005,19(2):106-109.

[15] 张锍仁. Fuzzy数的Fuzzy度量空间[J]. 北京师范大学学报(自然科学版),1999,35(2):162-166.

[16] 郭嗣琮. 模糊值函数分析学的结构元方法(II)[J]. 辽宁工程技术大学学报,2002,21(6):808-810.

[17] GOETSCHEL R, VOXMAN W. Elementary fuzzy calculus[J]. Fuzzy Sets and Systems,2005,19(1):82-86.

[18] PURI M L, RALESCU D A. Differentials on fuzzy functions[J]. J Math Anal Appl,1983,91(2):552-558.

[19] KALEVA O. Fuzzy differential equation[J]. Fuzzy Sets and Systems,1987,24(3):301-317.

[20] 杨乔,贠慧萍. 基于新模糊数的模糊距离的多属性决策方法[J]. 华北水利水电学院学报,2006,27(3):107-109.

[21] 王茹. 基于新的模糊距离在多属性决策上的应用[J]. 湖北汽车工业学院学报,2007,21(3):58-60.

[22] 杨纶标,高英仪,凌卫新. 模糊数学原理及应用[M]. 广州:华南理工大学出版社,2001:117-125.

[23] 华东师范大学数学系. 数学分析上册[M]. 3版. 北京:高等教育出版社,1981:23-55.

2010MSC：94D05; 03B52; 03E72; 28E10

(编辑 李德华)

New Definition and Properties of Fuzzy Valued Function Limit Based on Structural Element

SHU Tianjun, MO Zhiwen

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Using a kind of fuzzy distance, we give a new definition for the limit of fuzzy valued function which is generated structural element and use it to prove six theorems, which are addition together with multiplication, local boundedness, uniqueness, local protection, local protection and forcing convergence of the limit of fuzzy valued function which is generated structural elements. Finally, a Cauchy criterion theorem for the existence of the limit of fuzzy valued function which is generated structural elements is given.

Fuzzy distance; structural element; Fuzzy valued function; limit

O159

A

1001-8395(2017)06-0747-06

10.3969/j.issn.1001-8395.2017.06.007

2016-08-10

国家自然科学基金(11671284)和教育部博士点专项基金(20135134110003)

*通信作者简介：莫智文(1962—),男,教授,主要从事人工智能、模糊语言、粗糙集、量子信息处理的研究,E-mail:mozhiwen@263.net