与 Euler-Mascheroni 常数有关的几个不等式

陈金金, 王连堂

(西北大学 数学学院, 陕西 西安 710127)

与 Euler-Mascheroni 常数有关的几个不等式

陈金金, 王连堂*

(西北大学 数学学院, 陕西 西安 710127)

首先给出几个新的收敛序列,然后给出更一般的收敛序列来提高其收敛速度,得到几个与Euler-Mascheroni常数有关的不等式.

Euler-Mascheroni常数; Psi函数; 不等式; 收敛速度

Euler-Mascheroni常数γ=0.577 215 664…被定义为序列

的极限.众所周知, Euler-Mascheroni常数在数学和科学领域中扮演着重要的地位,它的理论还应用在数论、物理学、微积分学等方面.许多研究者在Euler-Mascheroni常数理论和建立相应不等式方面做出了许多贡献,例如

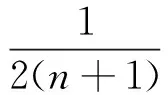
(1)

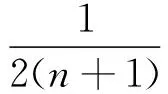
(2)

后来,D. W. DeTemple[1]通过研究序列

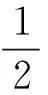
从而改进了收敛到γ的速度,并且得到不等式

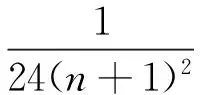
(3)

C. Mortici[2]再次研究了Euler-Mascheroni常数,同时定义了一种新的序列

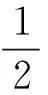
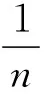
其中P、Q是关于n的多项式,且degP-degQ=1.

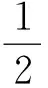
A. Vernescu[3]研究了序列

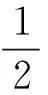
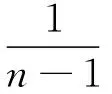
并得到不等式

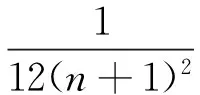
(4)

D. W. Lu[4]研究了序列

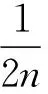
并得到

在证明主要定理之前,先给出一些结论.

欧拉伽马函数的表达式为

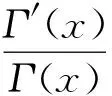
下面是关于Psi函数的渐近公式及不等式[5-7]:

(5)

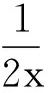
ψ(x+1)-lnxlt;

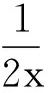
(6)

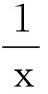
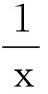
(7)

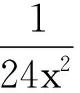
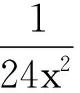
(8)

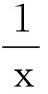
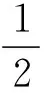
1 引理

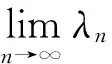
2 主要结论和证明

给定参数a、b和c某些特殊的值,使得下列序列收敛

利用上式,可得

Tn-Tn+1=

lnn+ln(n+1),

(10)

令

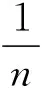
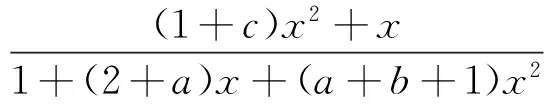
ln(1+x).

(11)

通过Mathematic计算,求得函数f(x)在x=0处的泰勒展开式为

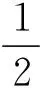
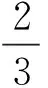
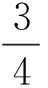
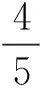
4a-6a2-4a3-a4+6b+8ab+3a2b-b2+

4c+6ac+4a2c+a3c-4bc-2abc)x5+O(x6),

则

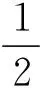
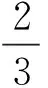
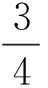
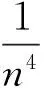
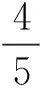
8ab+3a2b-b2+4c+6ac+4a2c+a3c-

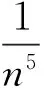
从而可以得到下面的定理.

定理2.1如果定义γa,b,c为序列Tn的极限,则有:

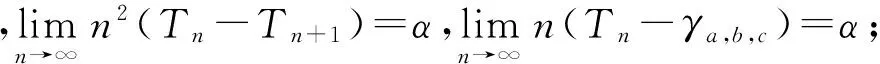
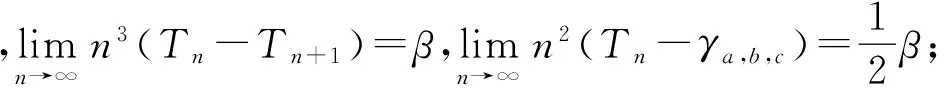
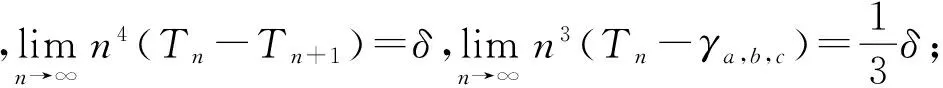
其中

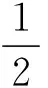
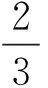
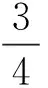
2ab-3c-3ac-a2c+bc;

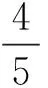
6b+8ab+3a2b-b2+4c+6ac+

4a2c+a3c-4bc-2abc.

定理2.2对n∈N,n≥1有:

(12)

(13)

其中

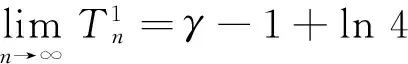
证明证明(12)式,通过计算得

由文献[9]知:

则计算可得:

对(12)式右边,利用(8)式右边得

(155+310n-294n2-588n3+1 680n4-

16 800n5)/[40 320n6(2n+1)]lt;0,n≥1,

对(12)式左边,利用(8)式左边得

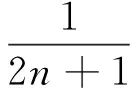
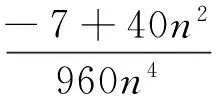
证明(13)式,通过计算得

则计算可得

对(13)式右边,利用(6)式右边得

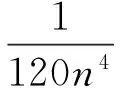
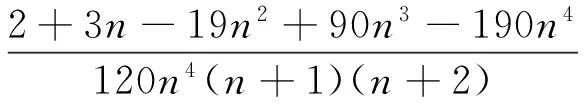
对(13)式左边,利用(6)式左边得

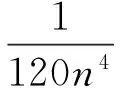
(-60-130n+36n2+253n3-1 071n4+

4 872n5+9 450n6+840n7)/

[2 520n6(n+1)(n+2)(2n+3)]gt;0,n≥1.

定理2.3对n∈N,n≥1有:

(14)

(15)

其中

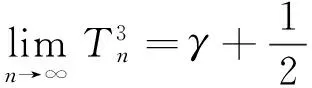
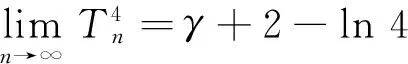
证明证明(14)式,通过计算得

则计算可得

对(14)式右边,利用(6)式右边得

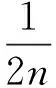
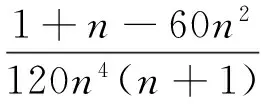
对(14)式左边,利用(6)式左边得

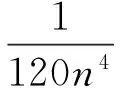
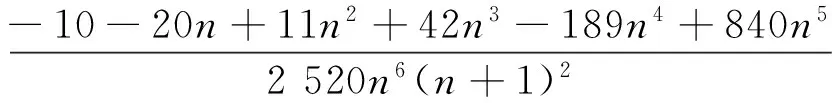
n≥1.

证明(15)式,通过计算得

由文献[9],则计算可得

对(15)式右边,利用(6)和(8)式得

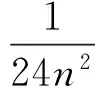
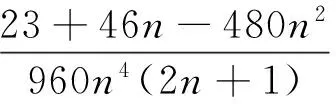
对(15)式左边,利用(6)和(8)式得

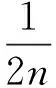
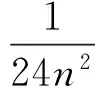
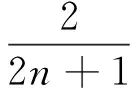
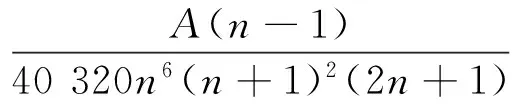
其中

A(n)=31 092+194 284n+475 633n2+

612 754n3+442 890n4+169 932n5+26 880n6.

为了提高这些序列收敛到γ的速度,给出了该序列更一般的形式来提高其收敛速度.对s∈N,有下列序列

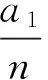
其中

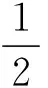
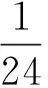
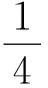
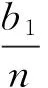
其中

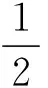
如果a=1,b=0,c=2,则有

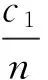
其中

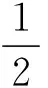
特别地,令

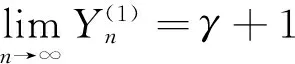
定理2.4对n∈N,n≥1,则有:

(16)

(17)

(18)

证明证明(16)式,通过计算得

令

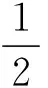
求导得

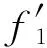
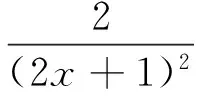
再利用(9)式右边得

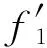
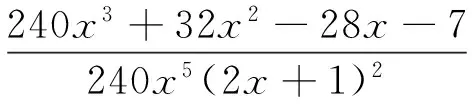
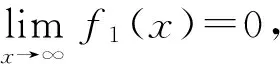
令

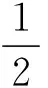
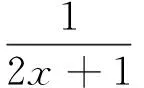
求导得

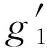
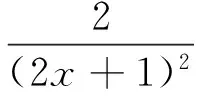
再利用(9)式左边得

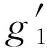
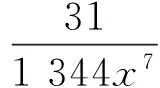
(-6 720x8-5 824x7+784x6-360x5-

684x4+2 503x3+2 749x2+1 085x+

155)/[6 720x7(x+1)3(2x+1)2]lt;0,x≥1,

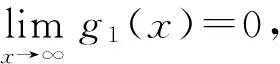
证明(17)式,通过计算得

令

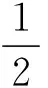
求导得

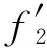
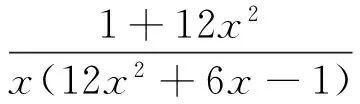
再利用(9)式左边得

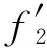
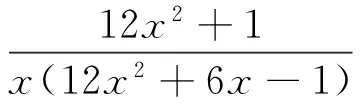
(38 528x6+39 872x5+1 072x4-11 608x3-

5 156x2-310x+155)/[6 720x7(2x+1)2×

(12x2+6x-1)]gt;0,x≥1,

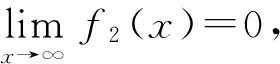
令

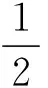
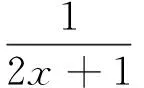
求导得

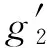
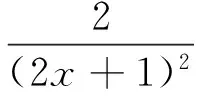
再利用(9)式右边得

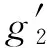
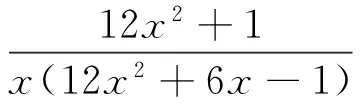
(-4 384x8-10 352x7-8 304x6-832x5+

2 585x4+1 496x3+258x2-14x-

7)/[240x5(x+1)4(2x+1)2×

(12x2+6x-1)]lt;0,x≥1,

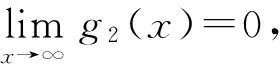
证明(18)式,通过计算得

令

f3(x)=-ψ(x+1)+

求导得

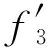
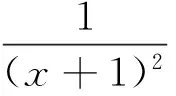
再利用(7)式右边得

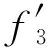
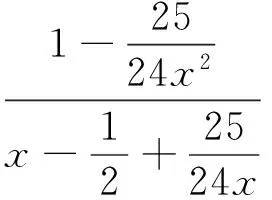
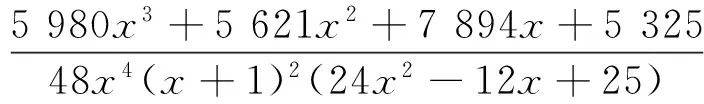
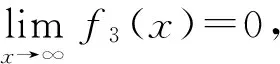
令

g3(x)=-ψ(x+1)+

求导得

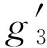
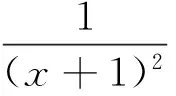
再利用(7)式左边得

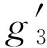
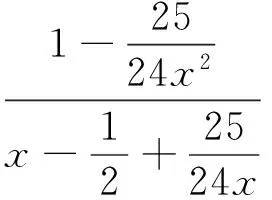
(-72 148x6-13 663x5-5 512x4+

472x3+8x2+704x+200)/[240x5(x+1)4×

(24x2-12x+25)]lt;0,x≥1,

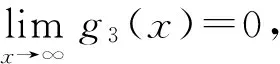
推论若

则对ngt;2有

证明经计算得

Pn-γ-1+ln 4=2ψ(n+1)-

再利用(6)和(8)式可得

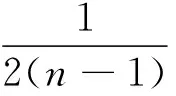
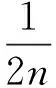
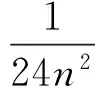
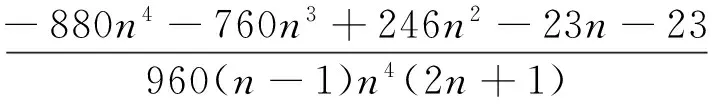
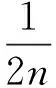
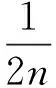
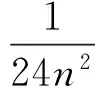
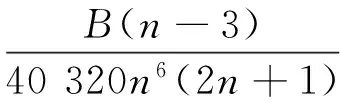
其中

B(n)=3 360n5+42 000n4+203 532n3+

471 954n2+510 610n+193 613.

[1] DETEMPLE D W. A quicker convergence to Euler’s constant[J]. Am Math Monthly,1993,100(100):468-470.

[2] MORTICI C. On new sequences converging towards the Euler-Mascheroni constant[J]. Comput Math Appl,2010,59(8):2610-2614.

[3] VERNESCU A. A new accelerate convergence to the constant of Euler[J]. Gaz Mat Ser A Bucha-rest,1999,104(4):273-278.

[4] LU D W. Some new convergent sequences and inequalities of Euler’s constant[J]. J Math Anal Appl,2014,419(1):541-552.

[5] CHEN C P, MORTICI C. New sequence converging towards the Euler-Mascheroni constant[J]. Comput Math Appl,2012,64(4):391-398.

[6] CHEN C P. Inequalities and asymptotic expansions for the psi function and the Euler-Mascheroni constant[J]. J Number Theory,2016,163(7):596-607.

[7] CHEN C P. Inequalities for the Lugo and Euler-Mascheroni constants[J]. Appl Math Lett,2012,25(5):787-792.

[8] MORTICI C. New approximations of the gamma function in terms of the digamma function[J]. Appl Math Lett,2010,23(1):97-100.

[9] CHEN C P, MORTICI C. Limits and inequalities associated with the Euler-Mascheroni constant[J]. Appl Math Comput,2013,219:9755-9761.

[10] NEGOI T. A faster convergence to the constant of Euler[J]. Gaz Mat Ser,1997,A15:111-113.

[11] RIPPON P J. Convergence with pictures[J]. Am Math Monthly,1986,93:476-478.

[12] YOUNG R M. Euler’s constant[J]. Math Gaz,1991,75(472):187-190.

[13] TIMS S R, TYRRELL J A. 3295. Approximate evaluation of Euler’s constant[J]. Math Gaz,1971,55(391):65-67.

[14] MORTICI C. Product approximations via asymptotic integration[J]. Am Math Monthly,2010,117(5):434-441.

[15] MORTICI C. Optimizing the rate of convergence in some new classes of sequences convergent to Euler’s constant[J]. Anal Appl,2010,8(1):99-107.

2010MSC：11Y60; 40A05; 41A25

(编辑 郑月蓉)

Some Inequalities Related to the Euler-Mascheroni Constant

CHEN Jinjin, WANG Liantang

(SchoolofMathematics,NorthwestUniversity,Xi’an710127,Shaanxi)

In this paper we give some new convergent sequences. Then we provide some more general convergent sequences to accelerate their convergence rates, and obtain some inequalities related to the Euler-Mascheroni constant.

Euler-Mascheroni constant; Psi function; inequality; speed of convergence.

O174.66; O178

A

1001-8395(2017)06-0731-07

10.3969/j.issn.1001-8395.2017.06.004

2016-11-20

陕西省自然科学基金(2010JM1017)

*通信作者简介：王连堂(1959—),男,教授,主要从事数学物理方程反问题、不适定问题解法的研究,E-mail:wlt800@sina.com