一道课本例题的研究及应用

陕西 吕二动 姬亚鹏

一道课本例题的研究及应用

陕西 吕二动 姬亚鹏

本文就此不等式的证明及其应用进行讨论.

一、不等式的证明

【证法1】用比较法(教材证明方法)

又a，b，m∈R+且alt;b，所以b+mgt;0,b-agt;0，

【证法2】用分析法

即证明b(a+m)gt;a(b+m),

即证明bmgt;am,

即证明m(b-a)gt;0.

由于mgt;0,alt;b,所以上式成立.

【证法3】定比分点公式法

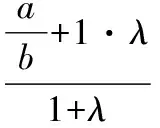
【证法4】斜率法

由不等式两边都是分式形式，可寻觅到这个式子隐含的几何背景——直线的斜率：

【证法5】构造函数法

又因为bgt;a,所以f(x)在[0，+∞)上是增函数.

除此之外，还有其他的解法，不再赘述.

二、不等式的应用

【解析】由“糖水变甜不等式”得

【例2】建筑学规定，民用住宅的窗户面积必须小于地板面积，但按采光标准，窗户面积与地板面积的比应不小于10%.并且这个比例越大，采光条件越好，问同时增加相同的窗户面积和地板面积，住宅的采光条件是变好了还是变坏了？

故住宅的采光条件是变好了.

【例3】一只口袋里装有4个红球和6个白球.

(Ⅰ)从口袋里任意摸出一个球，恰是红球的概率是多少？

(Ⅱ)再向口袋里放入2个红球，则从口袋里任意摸出一个球，恰好是红球的概率是变大还是变小？说明理由.

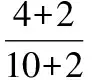
故该事件的概率变大了.

【证明】由于不等式右边是常数，为了便于求和，最好能把分母化为一致，

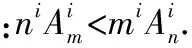
【证明】因为1lt;i≤mlt;n,所以n-i+1gt;m-i+1gt;0.

由“糖水变甜不等式”，有

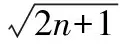
三、小试牛刀

【证明】在△ABC中，a+b-cgt;0.

【证明】由“糖水变甜不等式”得

【证明】由题设及“糖水变甜不等式”得

陕西省西安高新第三中学)