含参数的线性规划处理方法
福建 黄清波
含参数的线性规划处理方法
福建 黄清波
线性规划问题是高考的一个命题热点,其题型灵活多样,试题内容活泼、新颖.其中探究约束条件或线性目标函数中参数的取值(或范围),既是一个难点,又是一个常考点.高考对这类问题的考查可谓常考常新.学生解决这类问题之所以感觉困难,主要是因为这类问题含有参数从而使得要解决的问题处于动态变化之中,学生要么不知如何动笔,要么针对参数进行分类讨论时对变化因素考虑不周全而出错.对此,笔者通过对这一类题进一步分类及剖析,以期突破这一难点.
【类型一】目标函数中含有参数
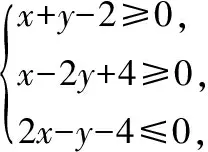
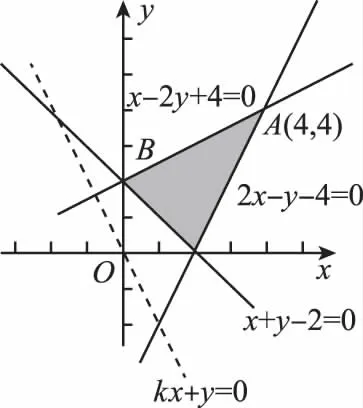
【分析】先画出可行域,得到交点坐标,再对k进行分类讨论,通过平移直线z=kx+y得到最大值点,即可求解.
解:约束条件所表示的区域为如图所示的阴影部分,其中点A(4,4),B(0,2),C(2,0).


综上所述,k=2.

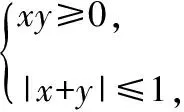
( )
A.0 B.-2
C.1 D.-1
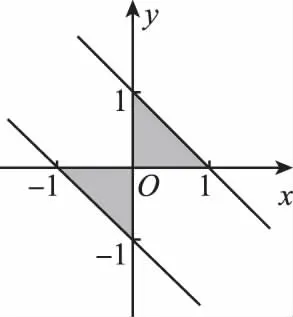
【分析】先画出可行域,利用z=ax+y取得最大值的最优解有两个,结合图形,确定a的取值即可得到结论.
解:约束条件所表示的区域为如图所示的阴影部分,因为z=ax+y取得最大值的最优解有两个,所以-a=1.所以当x=1,y=0或x=0,y=-1时,z=ax+y=-x+y有最小值-1,所以ax+y+1的最小值是0,故选A.
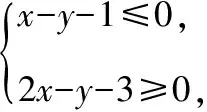
( )
A.5 B.4
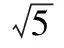
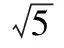
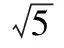
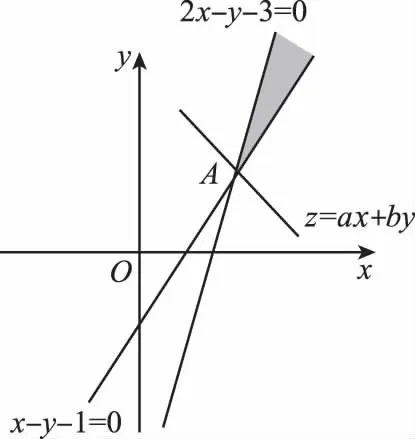
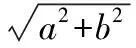
【小结】目标函数中的参数往往与直线的斜率有关,这类问题还有另一个特征,就是其最优解是可知的(一个、两个或无穷多个),因此解题时可充分利用斜率的特征加以转化.并且要特别注意目标函数中参数的位置,如目标函数是z=kx+y还是z=x+ky,这决定目标函数对应直线平移的方向是向上还是向下.
【类型二】约束条件中含有参数
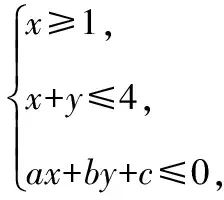
( )
A.2 B.1
C.-1 D.-2
【分析】逆向思维,从结论入手,将目标函数z=2x+y的最大值为7,最小值为1当成已知条件,对应于直线2x+y=7和2x+y=1,结合已知条件对应的直线x=1和x+y=4,通过作图与求解即可确定使得目标函数z=2x+y取得最大值与最小值的点M和N,然后将这两点的坐标代入直线ax+by+c=0,即可确定a,b,c之间的关系,进而使得问题得以顺利求解.
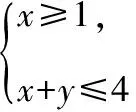

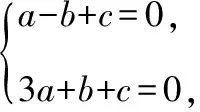
【点评】本题的求解方式是把结论看成已知,从已知求未知,打破了从正面入手根据图形找到使得目标函数取得最值的点来确定函数最值的常规求解思路,逆向思考问题,收到化繁为简、化难为易的解题效果.适时利用逆向思维解题,可以拓宽解题思路,加深对知识的理解和掌握,提高灵活运用知识的能力.

【分析】先画出可行域,利用目标函数的几何意义,即可得到结论.

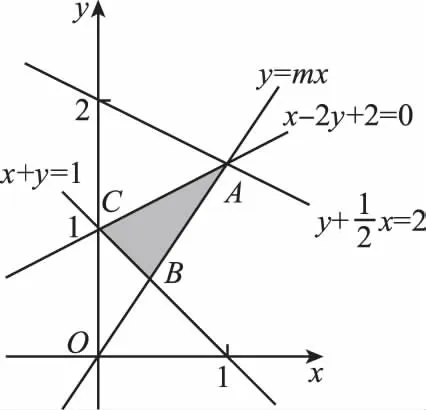
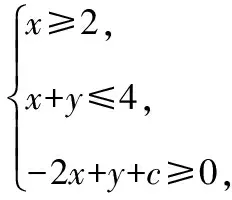
( )
A.10 B.12
C.14 D.15
【分析】先画出可行域,利用目标函数z=3x+y的最小值为5,建立条件关系即可求出c的值,然后求最大值即可.
解:当z=3x+y取最小值为5时,有3x+y=5,
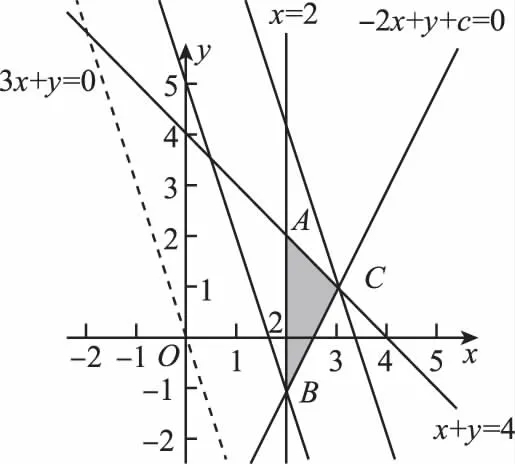
【小结】约束条件中的参数影响平面区域的形状,这时含有参数的不等式表示的区域的分界线是一条变动的直线,此时就要根据参数的取值确定这条直线的变化趋势,确定区域的可能形状,因此,增加了解题时画图分析的难度.求解这类问题时要有全局观念,结合目标函数逆向分析题意,整体把握解题的方向.
【类型三】目标函数、约束条件中都含有参数
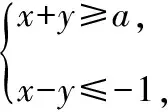
( )
A.-5 B.3
C.-5或3 D.5或-3
【分析】由约束条件作出可行域,然后对a进行分类,利用数形结合分类讨论建立方程关系即可求出a的值.
解:当a=0时,显然不满足题意.
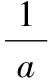
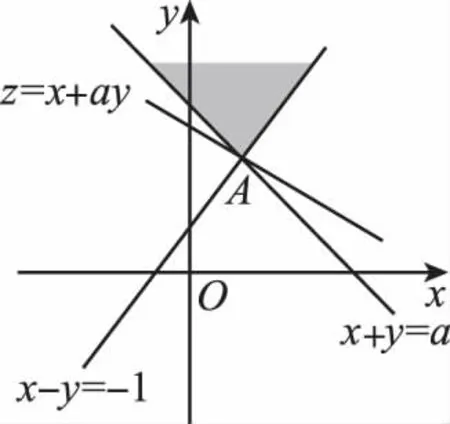


综上,a的值为3,故选B.

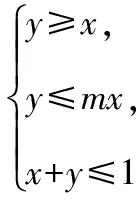
( )

C.(1,3)
D.(3,+∞)

福建省南安市国光第二中学)

