圆周运动临界问题的题型及其求解
河北
孙学礼
圆周运动临界问题的题型及其求解

孙学礼
在一定束缚条件下的圆周运动是典型的变速圆周运动,在变速圆周运动中经常出现“刚好”“恰好”“正好”“最大”“最小”“至少”等字眼,这些关键词恰恰说明此题中含有临界条件,而高考对圆周运动中含有临界条件试题的考查几乎每年都会出现。
对于圆周运动中的临界问题,分析时应首先考虑达到临界条件时物体所处的状态,然后分析该状态下物体的受力特点,结合圆周运动知识,列出相应的动力学方程,对有关范围类的临界问题,应注意分析两个极端状态,以确定变化范围。
一、水平面上的临界情况
水平面内做圆周运动的物体其向心力可能由弹力、摩擦力等力提供,常涉及绳的张紧与松弛、接触面分离等临界状态。在水平面内做圆周运动的物体,当角速度ω变化时,物体有远离或向着圆心运动的趋势,这时要根据物体的受力情况,判断物体所受的某个力是否存在以及这个力存在时大小或方向的变化,特别是绳的拉力、弹簧的拉力、接触面的弹力和摩擦力等,通过受力分析来确定临界条件和临界状态,是较常使用的解题方法。
【例1】如图1示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l。木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是
( )
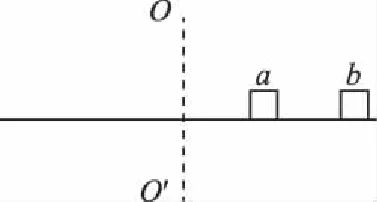
图1
A.b一定比a先开始滑动
B.a、b所受的摩擦力始终相等
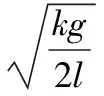
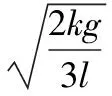
【解析】本题应该从向心力来源入手,分析发生相对滑动的临界条件。关键语句“两个质量均为m的小木块”暗示二者所受最大静摩擦力相同;而“放在水平圆盘”则提示二者具有相同的角速度;由于二者与转轴的距离不同,则转动中所受到的向心力不同。
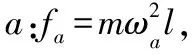
【答案】AC
【例2】如图2示,用一根长为l=1 m的细线,一端系一质量为m=1 kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT。g取10 m/s2,下列说法正确的是
( )
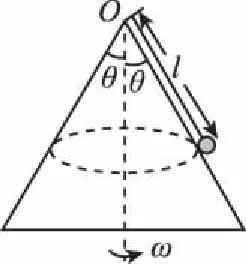
图2
【解析】本题中,尽管小球在锥体的表面运动,但是由于小球是在水平面内绕锥体的轴做圆周运动,因此仍然属于水平面上的圆周运动。
(1)若要小球刚好离开锥面,则小球受到重力和细线拉力如图3所示。小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平。
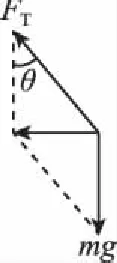
图3
在水平方向运用牛顿第二定律及向心力公式
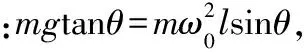
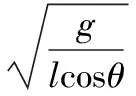
(2)同理,当细线与竖直方向成60°角时,由牛顿第二定律及向心力公式
有:mgtanα=mω′2lsinα
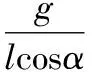
【答案】AC
二、竖直面上的临界情况
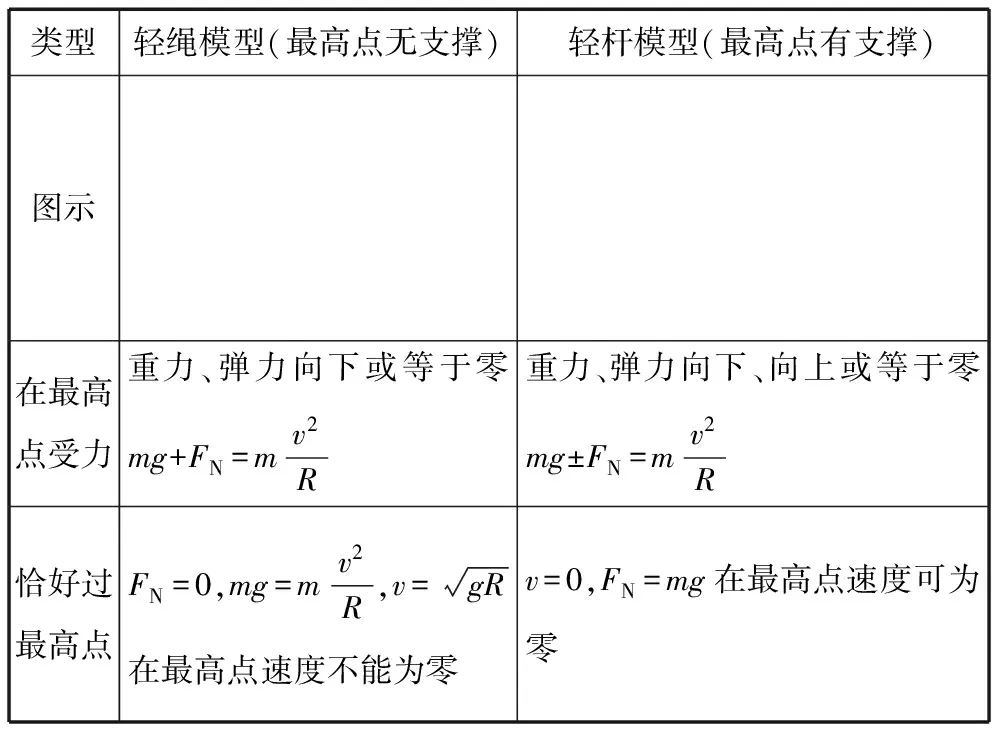
在竖直平面内做圆周运动的物体,运动至轨道最高点时的受力情况可分为两类,即“轻绳模型”和“轻杆模型”。它们的共同特点是物体在竖直平面内做变速圆周运动,这两类模型常伴有“最大”“最小”“刚好”等词语,是典型的涉及临界(极值)的问题,两种模型分析比较如下:

类型轻绳模型(最高点无支撑)轻杆模型(最高点有支撑)实例球与绳连接、水流星、翻滚过山车球与杆连接、球与竖直管道、套在圆环上的物体等
续表
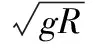
【例3】如图4所示,乘坐游乐园的翻滚过山车时,质量为m的人随车在竖直平面内旋转,下列说法正确的是
( )

图4
A.过山车在最高点时人处于倒坐状态,全靠保险带拉住,没有保险带,人就会掉下来
B.人在最高点时对座位不可能产生大小为mg的压力
C.人在最低点时对座位的压力等于mg
D.人在最低点时对座位的压力大于mg
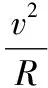
【答案】D
【例4】如图5所示,轻杆长3L,在杆两端分别固定质量均为m的球A和B,光滑水平转轴穿过杆上距球A为L处的O点,外界给系统一定能量后,杆和球在竖直平面内转动,球B运动到最高点时,杆对球B恰好无作用力。忽略空气阻力。则球B在最高点时
( )
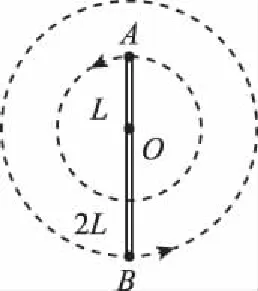
图5
A.球B的速度为零
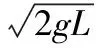
C.水平转轴对杆的作用力为1.5mg
D.水平转轴对杆的作用力为2.5mg
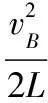
【答案】C
三、斜面上的临界情况
当物体在斜面上运动时,需要正确找出圆周运动的圆心和半径,解题的关键仍然是确定临界状态并找出满足临界状态的条件。而由于物体在斜面上运动,所以向心力的来源不像上述两种情况那么简单,必须确定物体在斜面方向上的受力,如重力沿斜面方向的分力mgsinθ;当物体与斜面之间存在摩擦时,摩擦力也可能参与提供向心力,这时的摩擦力也不再是简单的μmg,而是变成了μmgcosθ,这些都需要根据实际情况确定。
【例5】如图6所示,在倾角为α=30°的光滑斜面上,有一根长为L=0.8 m的细绳,一端固定在O点,另一端系一质量为m=0.2 kg的小球,小球沿斜面做圆周运动,若使小球能在斜面上做完整的圆周运动(g取10 m/s2),则小球在最高点A的最小速度是
( )
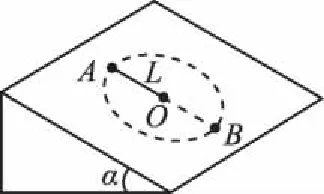
图6
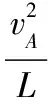
【答案】A
四、圆周运动与平抛运动的综合
圆周运动和平抛运动是两种典型的曲线运动,圆周运动与平抛运动结合的综合问题,是高考的热点,也是高考的重点。此类综合问题主要是水平面内的圆周运动与平抛运动的综合考查和竖直面内圆周运动与平抛运动的综合考查,首先根据运动的独立性和各自的运动规律列式,其次寻找两种运动的结合点,找出有关物理量之间的关系列式求解。
【例6】如图7所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动。现测得转台半径R=0.5 m,离水平地面的高度H=0.8 m,物块平抛落地过程水平位移的大小s=0.4 m。设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10 m/s2。求:
(1)物块做平抛运动的初速度大小v0;
(2)物块与转台间的动摩擦因数μ。
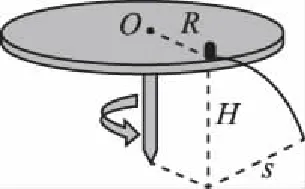
图7
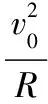
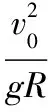
河北省衡水市郑口中学)

