求解物体平衡问题的三种方法
湖北
许 文
抓基础,重方法,理思路,破难点。
求解物体平衡问题的三种方法

许 文
共点力作用下物体的平衡问题,是历年高考中重点考查内容之一,在近几年的全国卷与各地方卷中都有所体现,且考查非常灵活。高考命题的热点主要表现在:(1)受力分析与共点力平衡问题;(2)动态平衡问题;(3)平衡中的临界与极值问题;(4)多物体相互作用下的平衡问题。
平衡状态是指物体处于静止或做匀速直线运动状态。平衡条件是物体受到的合力为零,即:F合= 0 。求解物体的平衡问题有三种方法:解析法、图解法、能量法。本文通过实例解析,帮助同学们有效地掌握物体平衡问题的求解方法。
一、解析法与图解法
解析法:当物体受到的几个共点力的合力为零时,沿任何一个方向上的合力均为零。若建立一个直角坐标系,将各力进行正交分解,分别在x、y方向上列出力的平衡方程,即:Fx=0,Fy=0;从而进行分析与求解。
图解法:当物体受到的几个共点力的合力为零时,平移这几个力的矢量,可以组成一个首尾相接的矢量图形,再通过此矢量图形进行分析与求解。
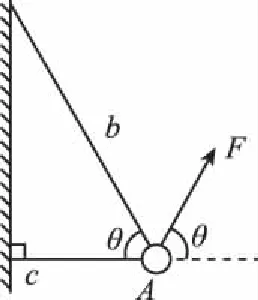
图1
【例1】如图1所示,物体A的质量m=2 kg,两根轻细绳b和c的一端连接于竖直墙上,另一端系于物体A上,两绳的夹角θ=60°。在物体A上另施加一个与水平线也成θ角的拉力F,若要使两绳都能伸直,求拉力F的取值范围。(g取 10 m/s2)
【解法1】 以小球为坐标原点建立如图2所示的直角坐标系,设b、c两绳上的张力大小分别为Fb、Fc,小球的受力如图2所示
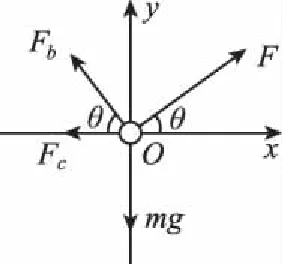
图2
由力的平衡条件得
Fsinθ+Fbsinθ-mg=0 (1)
Fcosθ-Fbcosθ-Fc=0 (2)
由(1)式知:当b绳刚好伸直即Fb= 0时,拉力F有最大值

由(1)(2)式得:2Fcosθsinθ=mgcosθ+Fcsinθ(3)
由(3)式知:当c绳刚好伸直即Fc=0时,拉力F有最小值




图3

【点评】 本题属于力的平衡中临界与极值问题。解法1用到了解析法,利用力的平衡条件列出相关变量的表达式,通过表达式来寻找问题的临界状态与极值,这是一种利用数学函数求物理极值问题的方法;解法2用到了图解法,通过力的矢量图形可以较简洁地找到问题的临界状态与极值,这种解法更体现了问题的物理本质。在定性分析动态平衡问题时,图解法往往比解析法显得更直观、更简洁、更有效。
【例2】如图4所示,一小球被水平细线OA与斜细线OB拉着处于静止。现将整个装置以C点为轴逆时针缓慢地转90°,在此过程中,关于线OA、OB上的拉力大小FA、FB的变化是
( )
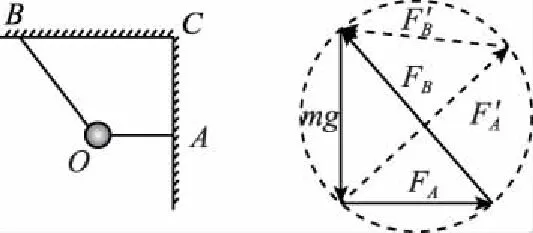
图4, 图5
A.FA一直变大 B.FA先变大后变小
C.FB一直变小 D.FB先变大后变小
【解析】在转动的过程中,小球受到的重力mg、FA、FB三个共点力的合力为零,平移这三个力将组成力的矢量三角形。由于力FA、FB的大小与方向均在变化,这会给作图会增加一定的困难。但要注意到矢量FA与FB的夹角不变化,且FA与FB的交点在以矢量FB的中点为圆心的圆周上移动,我们就可作出如图5所示力的矢量图。开始时力FA矢量水平,力FB矢量为圆的直径。在转动过程中,从图5中可以直观地看出FA先变大后变小,FB一直变小。
【答案】BC
【点评】用图解法分析动态平衡问题时,若有多个力的方向变化,要注意寻找其方向变化的特点。这些特点是进行作图的依据,从而避免作图的盲目性。
【例3】如图6所示,在半径为R的固定的竖直光滑圆环上套有两个带电小球a、b,开始平衡时两小球位置关于最低点c对称,且两小球的初始距离也为R。现用外力将小球a缓慢推至c点,此过程中圆环对小球b的弹力将
( )

图6
A.变大 B.变小 C.不变 D.无法判断
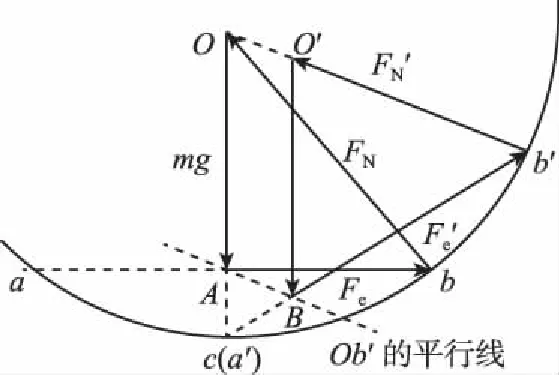
图7
【答案】B
【点评】本题中小球b在此过程中受到的重力mg大小与方向均不变,Fe与FN这两个力的大小与方向均在变化,但由于Fe在两小球的连线上,而FN的方向总指向圆环的圆心O,且Fe与FN的交点在圆环上移动。根据这些特点作出如图7所示的初态与末态力的矢量图形,能将问题化“动”为“静”,顺利地求解。
二、能量法
力与能是分析处理力学问题的基本观点。如果相互作用的一个系统在运动过程中遵循机械能守恒定律,则系统运动到平衡状态时其势能最小,动能最大。在求解相互作用系统的平衡问题时,我们可以假设让系统做满足机械能守恒的某种运动,当系统运动到平衡状态时其动能有最大值。
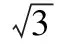
( )

图8
A.45° B.30° C.22.5° D.15°
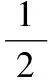
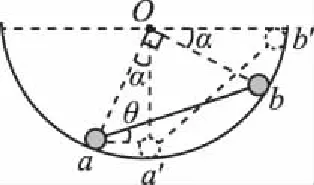
图9
由上式知当α=30°,即θ=90°-45°-α=15°时Ek最大,这时系统的势能最小,系统处于平衡状态,即在题中的平衡状态下θ=15°。
【答案】D

湖北省武汉市华中科技大学附属中学)
依据大纲抓重点,研究命题攻难点。

