动量和能量综合四大模型归纳
浙江
汪显和
三把“金钥匙”开启四类“不能再”现象。
动量和能量综合四大模型归纳

汪显和
动量守恒问题是新高考中的一大亮点,这块曾经几乎被搁置起来的重要的物理学知识在新高考中开始显得极为重要。在考题中往往将动量的问题和能量的问题结合起来,联系生活中的情景,形成一类难度较大的综合题,使得许多同学在解题过程中感觉难度很大,容易失分。总结动量和能量综合大题的分析,笔者认为此类问题最为关键的核心部分可以归纳为四种模型。相关的动量能量的综合问题几乎都是这四种当中的某一类或者是几类合成起来的,具体解题过程中我们只要能够找出问题的最根本的模型就可能快速、准确地将问题予以解决。
一、“穿到不能再穿”模型
【例1】如图1所示,光滑水平面上质量为M的木块在水平面上处于静止状态,有一质量为m的子弹以水平速度v0击中木块并与其一起运动,求系统所产生的内能?

图1
【解析】取子弹和木块为参考系。由于地面光滑,故系统的动量守恒。取向右为正方向。
根据动量守恒定律有:mv0=(M+m)v
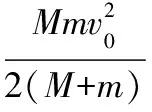
【总结】这种子弹穿入木块最后达到两者相对静止的状态,我们总结为“穿到不能再穿”的模型。子弹打击木块的时间非常短,假如没有“光滑水平面”的条件,子弹穿入木块的过程也可以认为系统的动量守恒,也可以应用动量守恒定律进行求解。
二、“滑到不能再滑”模型
【例2】图2所示,在光滑的水平面上有一块质量为M的粗糙木板,一质量为m的物块以速度v0滑上木板的左端,物块与木板的动摩擦因数为μ。要使木块不会从木板右端掉下来,则木板的长度至少要多长?

图2
【解析】取物块和木板为系统研究。由于地面光滑,故系统的动量守恒。要使m不会从M的右端滑下来,临界的状态是m刚好滑到M最右端的时候两者相对静止,即有共同的速度v。取初速度的方向为正方向。
根据动量守恒定律有:mv0=(M+m)v
在滑动过程中系统减少的动能转化为内能
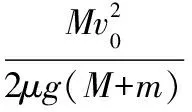
【总结】像这种小物块在木板发生相对滑动最后达到两者相对静止的状态,我们把它总结为“滑到不能再滑”的模型。
三、“压到不能再压”模型
【例3】如图3所示,光滑水平面上有质量分别为m1、m2的A、B两物体。静止物体B左侧固定一处于原长的轻弹簧,物体A以初速度v0水平向右运动,接触弹簧以后将压缩弹簧,求在压缩弹簧过程中弹簧的最大弹性势能。
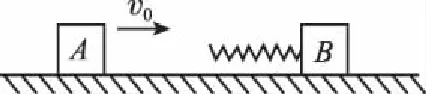
图3
【解析】A、B和弹簧为研究系统。由于地面光滑,故系统的动量守恒。由于刚开始的时候B是静止不动的,A运动一段时间后与弹簧接触,弹簧将会被压缩。压缩的弹簧对A有向左的力,故A减速,弹簧对B有向右的力,故B加速。总有一个时刻A的速度和B的速度相等,即A、B有共同速度,此时刻两者相距最近。此时的弹簧压缩量最大,弹性势能最大。取向右为正方向。
系统减少的动能转化成为弹簧的弹性势能。
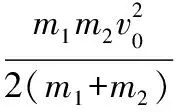
【总结】这个模型中,由于开始A的速度大于B的速度,两者距离逐渐减小弹性势能增大,当A的速度小于B的速度时两者之间的距离增大弹性势能减小;A、B间距离最小,也就是压到不能再压的时候,弹簧的弹性势能最大,这就是“压到不能再压”模型。对于这个模型,假如说A与弹簧接触后就被粘连,那么可以让我们同学分析,A接触弹簧之后由A、弹簧、B组成系统的运动的情况,以及能量和动量的变化的情况。
四、“升到不能再升”模型
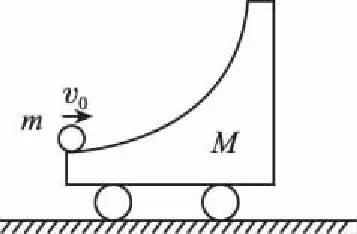
图4
【例4】如图4所示,质量为M的带有圆弧曲面的小车静止在光滑水平面上,另有一质量为m的小球以水平速度v0冲上小车的曲面。求m能够在小车的曲面上上升的最大高度。
所谓就业观,具体就是学生在参加工作选择某一职业时所表现出的一种态度和观念,它是学生对自己就业的一种反应性倾向,由行为倾向、情感倾向和认知倾向三大要素组成。对大学生而言,就业并不意味着就是简单地找一份工作,还与学生后期的人生发展与职业理想有着密不可分的必然联系。因此,学生在校期间,形成一种良好的就业观是其人生观、价值观和世界观的重要体现,对大学生未来职业发展的理想以及就业认知和就业心态及其后期在职场上所体现出的态度和修养也发挥着决定性作用。
【解析】对m和M整个系统而言,m在曲面向上运动的过程中,M也同时向右运动。由于m竖直方向上速度有向上的分量,可以知道系统的动量不守恒。但由于水平地面是光滑的,对系统而言在水平方向上的合力等于零,故系统在水平方向上动量守恒。另外从运动过程可以知道当小球在竖直方向上的分速度等于零时,小球到达最大高度,此时小球和小车具有共同的速度。取向右方向为正方向。
根据动量守恒定律可知:mv0=(M+m)v
系统减少的动能转化为小球上升过程中所增加的重力势能。
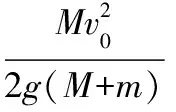
【总结】这个模型中,小球在上升的过程中,最后竖直方向上的分速度变为零,也就是说在竖直方向的能够上升的高度达到最大,我们称之为“升到不能再升”模型。对于此类模型往往系统的总动量并不守恒,但是在某一个方向上的动量确是守恒的,此时我们就要利用这个方向上的动量守恒进行问题的解决。
以上是动量和能量综合问题的四种核心关键模型。可以看出,动量和能量综合的问题关键在于确定研究的对象,然后找到动量守恒和能量守恒的过程,最后列出动量守恒和能量守恒的方程。对于动量守恒定律的关键是根据问题情境判断系统动量是否守恒,或者是在某一个方向上动量守恒。而能量守恒的关键在于搞清楚物体在运动过程中是什么能量和什么能量之间的转化,在转化过程中能量的定量关系如何,最后列出相关方程。联立动量守恒和能量守恒的相关方程,就可以解决问题。具体问题中的动量和能量的问题几乎都在这四种模型之内,或者就是这四种中的两种或多种的组合,解题过程中只要分析清楚问题的情景过程,明确各个物理过程中的动量和能量的相关情况,逐个联立方程就可解决问题。
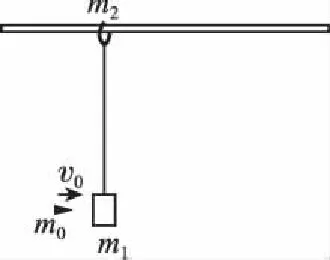
图5
【牛刀小试】如图5所示,质量为m2的小环穿在光滑水平细杆上。小环通过不可伸长的细线悬挂着质量为m1的木块。m1和m2处于静止状态。质量为m0的子弹以初速度v0水平射入木块并留在其中,求木块能够上升的最大高度。
【解析】这个问题涉及两个过程,分别对应两种模型。
过程一是“穿到不能再穿”的过程。这个过程中研究对象取m0和m1。由于作用时间非常短,两者之间产生很大的内力故子弹和木块的动量守恒。取初速度的方向为正方向,设子弹射入木块后木块和子弹的速度为v1,根据动量守恒定律有:m0v0=(m0+m1)v1。
过程二是“升到不能再升”的过程。这个过程中研究对象是子弹、木块和小环。这个系统的总动量不守恒,但是水平方向上动量守恒。当木块上升到最高点时,小环和木块有共同的速度。取向右为正方向。
根据动量守恒定律有:(m0+m1)v1=(m0+m1+m2)v2
在木块上升过程中,子弹和木块的重力势能增加,系统的动能减小转化为重力势能
根据能量守恒定律有:
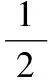
联立上述方程可以解得:
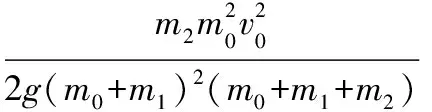
即木块能够上升的最大高度为
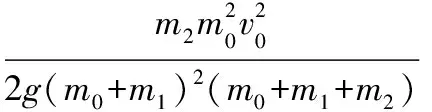
浙江省兰溪市第一中学)

