三点式LC振荡器的频率研究

邱月友 杨会成 赵秀华

（1.安徽工程大学电气工程学院 2.安徽省电气传动与控制重点实验室 安徽芜湖 241000）

三点式LC振荡器的频率研究

邱月友1,2杨会成 赵秀华

（1.安徽工程大学电气工程学院 2.安徽省电气传动与控制重点实验室 安徽芜湖 241000）

LC三点式振荡器具有结构简单、调谐方便等优点，被广泛用在电子电路中，特别是在通信系统和高频电子电路。三点式LC振荡器的频率研究中给出LC振荡器的两种典型模型，并进行简单分析。重点给出了两种典型电路的等效电路，在等效电路的基础上进行了振荡频率的推导。

LC振荡器；振荡条件；振荡频率；等效电路

在电子线路中，信号源通常是必不可少的部分，在通信系统中信号源常采用正弦波振荡器。所谓的振荡器是不需要外部输入激励信号、自身能将直流能量转换成交流能量的装置，所以又称之为自激振荡器。它与放大器最大的区别就是不需要外部输入信号，共同点是都能将直流能量转换为交流能量。根据自激振荡器产生的交流信号波形可分为正弦波和非正弦波两大类，而在通信系统中所用的高频振荡器大多为LC正反馈正弦波振荡器。

对于LC三点正反馈振荡器主要有两种形式：电容三点式和电感三点式。在实际应用中这两种形式都有应用，无论哪种形式都需要根据信号来确定振荡器的频率，然后再选择振荡器的参数。但很多文献中都没有对这两种形式的频率进行详细的推导，本文将给出这两种形式的等效电路，以及频率的详细推导。

一、电容三端式等效电路及频率

图1（a）是LC电容三点式振荡器的实际电路，（b）是其交流通路，（c）是其Y参数高频等效电路。

实际电路（a）图中既有直流分量的通路也有交流分量的通路，它实际反映了电路将直流能量转化为交流能量的电路。而真正能反映振荡器工作频率的是其交流通路。（b）图的交流通路虽然结构简单，但不易推导其频率与元件C、L之间的数学关系，所以我们可以从振荡器的Y参数等效电路（c）图中来推导其工作频率。

在图 1（c）中，Ub是输入量，U’b是反馈量，gie是输入电导、goe是输出电导、gm为跨导，gl是三极管以外的电路中所有电导折算在ce两端的总电导。假设goe、gl和C1三者并联等效阻抗为Z1，流过Z1的电流为I1；L、C2和gie的串并联等效阻抗为Z2，流过Z2的电流为I1，这样就可以将图1中的（c）图等效为图2。

图1 电容三点式振荡器

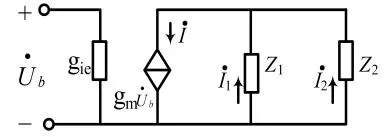
表2 Y参数等效电路

假设振荡器的振荡频率为ω。在图2中，根据分流公式有：

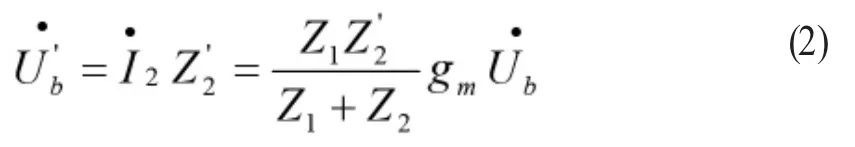
对于正反馈的LC振荡器来说，环路增益T(s)为：

因为,

将它们代入（3）式中可得到，

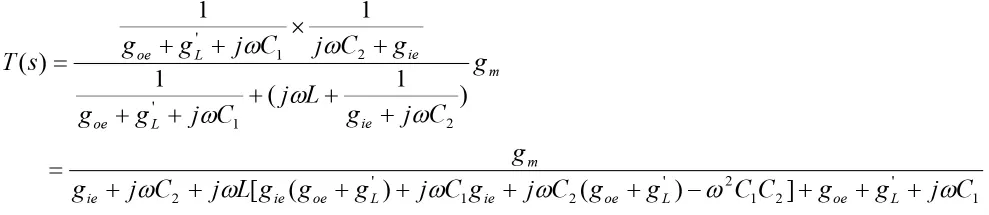
根据振荡条件，令T(s)虚部为0，即：

将（5）式变换可得：

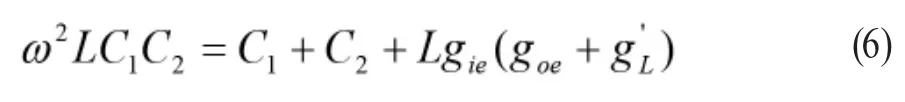
对于晶体管本身的参数等远远小于电路中的元件L、C的参数，也就是说在（7）式中第二项远小于第一项，所以在分析计算中振荡器的振荡频率可以近似的表示为：

即振荡器的振荡频率近似为LC回路的谐振频率。

二、电感三端式等效电路及频率

图3是LC电感三点式振荡器的电路，其中（a）是实际电路，（b）是其交流通路，（c）是其Y参数高频等效电路。

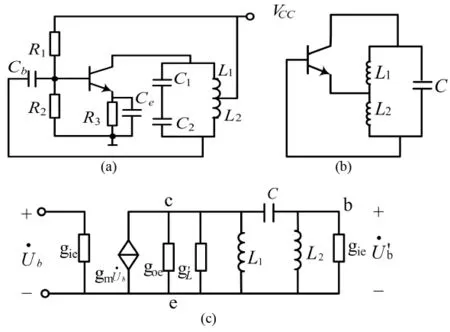
图3 电感三点式振荡器

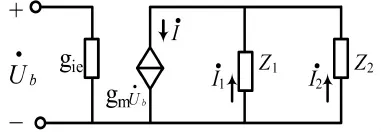
图4 Y参数等效电路

假设振荡器的振荡频率为ω。在图4中，根据分流公式有：

将（8）式代入可得：

对于正反馈的LC振荡器来说，环路增益T(s)为：

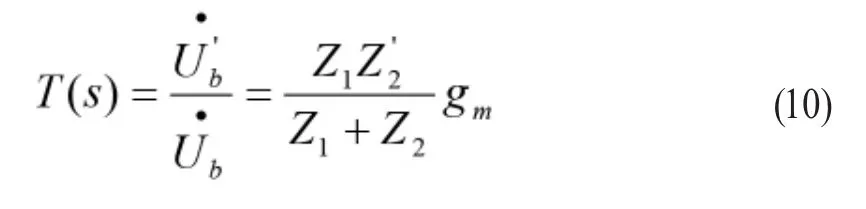
将 Z1、Z2及 Z'2代入（10）式后化简，并考虑电感 L1、L2之间的互感M，可得到T(s)表达式。与电容三点式LC振荡器类似，根据振荡器相位平衡条件，令T(s)虚部为0，有：

根据（11）式可得到：

同理，由于晶体管本身的参数等远远小于电路中的元件L、C的参数，所以电感三点式LC振荡器的振荡频率近似为（为LC回路的谐振频率。）：

三、两种典型LC三端式振荡器的比较

LC电容三点式振荡器和LC电感三点式振荡器在实际中都有应用，但两者又各自有各自的特点，现将两者的特点总结如下：

（1）在两种振荡器中，晶体管都存在极间电容，影响振荡器的工作频率。

对于电感三点式振荡器，晶体管的极间电容与电感并联，当工作频率较高时，有可能会使电抗性质发生变化，从而破坏了振荡条件，所以电感三点式振荡器的工作频率不能过高。而对于电容三点式振荡器，晶体管的极间电容与电容并联，并不会改变电抗性质，也就不会破坏振荡条件，所以电容三点式振荡器的工作频率可以较高。

（2）由于存在谐波分量的影响，两种振荡器输出的波形质量不同。

在LC三点式振荡器中存在非线性元件晶体管，并且振荡器稳定振荡时，晶体管工作在非线性状态，因此除了存在基波分量外，还含有少量的高次谐波分量。对于电感三点式振荡器，由于反馈是由电感产生的，高次谐波分量也会在其上产生压降，而且频率越高产生的压降越大（因为，即反馈到晶体管输入端的谐波压降越大，经三极管放大后输出较大谐波电压，较大地影响输出波形。而对于电容三点式振荡器，由于反馈是由电容产生的，谐波分量在其上产生的压降较小（因为，因此对输出波形的影响较小。

四、结语

LC振荡器广泛应用于各种电子电路中，因为不论是电容反馈振荡器还是电感反馈振荡器，线路都比较简单，容易起振。而且由于电容反馈振荡器具有工作频率高、输出波形好等优点，在很多场合得到更广泛地应用。同时，如果在振荡器中应用可调电容的话，可以构成频率可调的振荡器。但是在改变电容时，虽然可以改变电容反馈振荡器的频率，反馈系数也将改变（反馈系数F=C1/C2），很可能破坏振荡器的起振条件，所以对于典型的LC振荡器来说，工作频率的带宽不能很宽。为了扩展振荡器的带宽，需对LC反馈振荡器进行改进，这里就不再赘述。

[1]陈昌汉.高频电子线路[M].北京：高等教育出版社，2008，106-113.

[2]童诗白,华成英.模拟电子技术基础[M].北京：高等教育出版社，2010.

[3]清华大学通信教研组.高频电路[M].北京：人民邮电出版社，1979，476-488.

[4]张肃文,陆兆熊.高频电子线路[M].北京：高等教育出版社，2002，383-387.

[5]曾兴雯.高频电子线路[M].北京：高等教育出版社，2006，139-145.

[6]李永安，王革伟.一种分析LC振荡器的简便方法[J].咸阳师范学院学报，2005(2):81-82.

[7]唐民丽，吴恒玉.三点式LC振荡器的起振条件的分析[J].长沙大学学报，2005(5):75-76.

Frequency Analysis of Three Point LC Oscillator

Qiu Yueyou Yang Huicheng Zhao Xiuhua
(Anhui Polytechnic University,Anhui Provincial Key Laboratory of Electric and Control,Wuhu,Anhui 241000)

Three-point LC oscillator has simple structure and tuning conveniently advantages,so it is used in electronic circuit,especially communication system and radio-frequency electronic circuit.This paper gives and analyses two typical forms of LC oscillator and expressly gives their equivalent circuits,deducing frequencies based on their equivalent circuits.

LC oscillator;oscillating condition;oscillating frequency;equivalent circuit

TN752.2

A

2095-0438（2017）12-0153-04

2017-07-26

邱月友（1976-），男，安徽六安人，安徽工程大学电气工程学院讲师，硕士，研究方向：过程控制、通信电子、电子电路研究。

2017年高等教育提升计划项目（项目编号：TSKJ2017B28）；2014年安徽工程大学校级教学研究项目（项目编号：2014jyxm82）。

[责任编辑 王占峰]