桥梁体外预应力筋梁加固理论分析

彭 辉，谢俊武

(湖南省城交设计研究院有限公司，长沙 410114)

桥梁体外预应力筋梁加固理论分析

彭 辉，谢俊武

(湖南省城交设计研究院有限公司，长沙 410114)

体外预应力筋在在新桥梁建设和旧桥梁改造加固中运用广泛，此施工方法较为成熟，但并未对此施工方法的具体受力性质进行深入分析，究其根源是在桥梁外荷载的影响下结构与预应力筋梁会产生相对移动，已有定理中的变形协调假定不能准确的反映实际情况．基于此问题本文将体外预应力筋梁的滑移影响考虑进来，通过运用Euler-Bemoulli梁理论的假定条件和考虑体外预应力筋的实际变形情况，改进桥梁体外预应力分析理论，对工程设计具有一定参考价值．

预应力法；桥梁加固；体外预应力

随着工程中新型高强材料的发展和施工工艺技术的改进，预应力混凝土极大地促进了工程的发展[1]．目前预应力混凝土梁桥的发展尤为快捷．1955年第一座运用预应力混凝土技术简支梁桥诞生，促进人们对于预应力混凝土结构的理论研究，国内外学者对其展开深入研究，预应力混凝土桥梁在逐渐成为广泛运用的施工技术之一，所以国内外预应力混凝土桥梁结构基数较大，对于其具体受力理论研究十分迫切[2]．

体外预应力结构的具体施工工艺为，桥梁中后张力与盈利近视加固构架的主要受力部分，其中的锚固体系主要有桥梁外侧的锚固筋以及转向结构组成，这是桥梁加固中体外预应力结构的主要受力构件[3]．与体外预应力体系相比较的是体内预应力体系，其受力关系主要是桥梁结构面中粘结结构与非粘结结构的对应，两者组成了预应力后张法结构体系主体．

体外预应力结构体系技术正在不断完善与推广，常见于预应力混凝土桥梁结构加固、特种结构工程、重要的建筑工程及地下空间工程等领域，主要常见于新建桥梁结构及对于已有建筑结构物的维修与加固措施，对于桥梁结构体制系中无法设置预应力结构与临时性的桥梁预应力结构施工同样适用[4-6]．与传统的桥梁工程价股相对比，体外预应力法在材料用量上，相对于体内预应力混凝土用钢量大，设计为体外预应力结构可减少桥梁整体体积，一定程度上减少混凝土用量，桥梁上部自重的减少可促进下部结构的简化，从而在整体上降低桥梁自重[7]．在结构工程的使用耐久性方面对比，钢筋较多的设置在体内预应力结构中，浇筑混凝土时施工不便，混凝土与结构中容易产生空隙[8-10]．相对比而言体外预应力钢筋结构的布置较简单，进行混凝土浇筑施工时受施工工艺影响小，同时体外预应力结构设置在桥梁体系外，在工程使用过程中可对其进行检测、修复及加固等，对于桥梁结构本身的耐久性方面有显著的提高[11]．在桥梁工程的施工中使用体外预应力结构可加快工程施工进度，达到控制工程整体建设成本的目的；同时减少桥梁内部的预应力钢结构的施工，减少其摩擦损失[12]．传统的桥梁加固方法与体外预应力结构加固对比见表1．

表1 桥梁加固方法对比表

1 体外预应力混凝土加固方法

常见的矩形截面梁的锚固块施工法，将锚固处开洞施工，锚固块主要由钢管、钢束组成，这类型的锚固块施工简便，受力特点也较为简单，受力分析主要为钢管与钢束强度[13]．一般箱型桥梁的横截面和荷载较大，不宜采用矩形截面法计算，需要针新型的体外预应力加固方法进行计算推导公式．

加固效果是评价一种加固体系的最直接方法．对桥梁在进行新型体外预应力加固的正常使用极限状态和承载能力极限状态抗弯承载能力的计算分析对比，国内外学者对此做了大量研究工作，总结出了一系列方法经验[14]，但并未对梁结构在横向体外预应力加固下的受力分析．

针对于体外预应力结构在极限状态下的受力计算，许多研究者将普通钢筋总配筋量计算，由试验结论建立的半经验公式，并未从结构材料的特点出发考虑其受力问题，此类型的计算方法存在一定局限性．本文从箱梁结构的整体受力模型考虑十分必要，利用极限分析的方法分析预应力索加固体系的受力特征，对桥梁结构的整体加固效果进行合理评价．

桥梁体外预应力结构对于提高其抗弯能力有显著效果，从力学分析角度可较好地判断．但如何分析其抗剪能力的提高，此类方法计算不够简便．结构分析中将原结构剪力忽略，预应力结构在承受荷载时会减缓裂纹的发展，提高混凝土对钢筋的粘结力，提高整体桥梁的抗剪承载能力．

2 体外预应力混凝土梁的张拉受力分析

体外预应力结构的张拉施工是加固的主体，在体外预应力的施工过程中阶段施工法促进了受力的均匀性，张拉工艺的预应力体系受力情况对结构的寿命有显著影响，先从体外预应力的张拉受力分析计算[15]．

2.1 计算基本理论假设

从简单的平面直梁结构分析，方便与公式推导计算，假设体外预应力筋在平面直梁面內，详见图1．现对体外预应力筋结构作如下假设：

(1)假设体外预应力筋结构的形状由(n+1)个顶点的折线状态，每个顶点的偏心距用ei表示，其初始坐标用(xi，yi)(i=0，1，2……n)表示．产生位移变形每个顶点的位移变为(ui，vi)；

(2)假设体外预应力筋在顶点(x0，y0)和变形点(xn，yn)锚固在桥梁结构上；

(3)假设体外预应力筋的顶点(xi，yi)(i=0，1，2……n)处，体外预应力筋与结构转向装置接触面无摩擦力．

图1 体外预应力梁示意图

2.2 预应力筋和梁的相互作用

(1)预应力筋对梁的作用力，如图2所示.

图2 预应力筋对梁的作用力示意图

设预应力筋的张力是 T，在锚固点(x0，y0)处，预应力筋对梁的作用力是

式中Fx0、Fy0是结构锚固端处体外预应力的张力T的水平分力和竖向分力，q为1段预应力筋同水平线的角度，其表达式为

与桥梁结构锚固点(xn，yn)处，体外预应力筋对横梁的力是

式中Fxn、Fyn是预应力结构锚固端处预应力筋的张力T在水平分力与竖向分力，nθ为第n段体外预应力筋与水平向的角度，其表达式为

(2)结构转向装置对桥梁的作用力．结构转向装置(xi，yi)的作用力示意图，见图 3

图3 转向装置对梁的作用力示意图

预应力筋对梁的作用力为

式中Fxi、Fyi是体外预应力筋在转向装置的张力T在水平分力和竖向分力，nθ为第n段体外预应力筋与水平线的角度，其表达式为

(3)体外预应力筋对梁的受力根据式(1)～(5)可得，体外预应力筋对梁的作用力在X和Y产生的合力为

3 体外预应力张拉阶段梁的应变能

运用最小势能原理可知：在结构产生的变形挠度中，求得整个结构系统的总势能较小值．运用总势能的一阶求导计算，分析体外预应力量的平衡方程与边界条件．

体外预应力梁张拉阶段见图4．

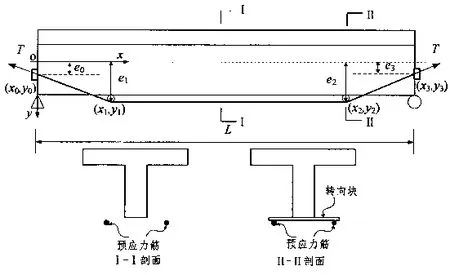
图4 体外预应力梁张拉阶段计算示意图

运用Euler-Bemoulli梁理论分析，计算得体外预应力梁张拉阶段的总势能为

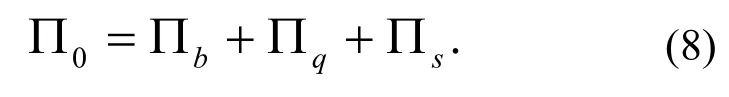
式中Πb表示桥梁弯曲应变能，Πq表示结构外力势能，Πs表示体外预应力筋应变能，其表达式为

将式(9)代入式(8)可以得到总势能的表达式

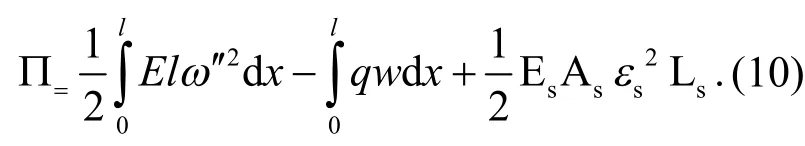
体外预应力筋中节点(xi，yi)位移为(ui，vi)，运用梁理论，结构转向块的位移运用梁的挠度和转角计算得

利用Euler-Bemoulli梁理论分析得

将式(12)、(11)代入式(6)可以得到

将式(12)代入式(9)，可求得体外预应力筋总应变计算公式

4 结论

运用变分原理得到体外预应力加固微分控制方程与边界条件，通过基于变分原理，考虑预应力筋处无摩擦力影响，运用Euler-Bemoull的梁理论假设，对体外预应力梁力学特性计算提出了新方法．

分析体外预应力筋的张拉阶段受力特点，运用最小势能原理计算体外预应力梁在初始状态下，得到其平衡微分控制方程与边界条件，对于体外预应力筋计算与施工有一定指导意义．

[1]熊学玉. 体外预应力结构设计[M]. 北京: 中国建筑工业出版社, 2005.

[2]KARAYANNIS C G. A model with tension softening for concrete beams under combined torsion, flexure, shear and prestressing[C]International Conference on Computational Structures Technology, Greece: Athens, 1994: 161-167.

[3]HERBRAND M. Shear tests on continuous prestressed concrete beams with external prestressing[J]. Structural Concrete, 2015,16(3): 428-437.

[4]GODAET B. Strengthening prestressed concrete box girder bridges: The french experience[J]. Structural Engineering International, 1995, 5(2): 81-84.

[5]LIN T Y, BURNS N H. Design of prestressed concrete structures[M]. Sahu Cement Service, 1964.

[6]李国平. 预应力混凝土结构设计原理[M]. 北京: 人民交通出版社, 2000.

[7]SENER M, UTKU S, WADA B K. Geometry control in prestressed adaptive space trusses[J]. Smart Materials &Structures, 1993, 205(2): 219-225.

[8]周履. 无粘结力筋与体外力筋预应力混凝土桥梁的发展历程与现状[J]. 桥梁建设, 1997(Sl): 1-12.

[9]Muller J. Construction of long key bridge[J]. Pci Journal, 1980,25(6): 97-111.

[10]徐栋. 桥梁体外预应力设计技术[M]. 北京: 人民交通出版社,2008.

[11]CARREIRA D J, POULOS T D. Designing for effects of creep and shrinkage in high-rise concrete buildings[J]. Aci Special Publication, 2007, 117(1): 74-79.

[12]FAN X, ZHANG W. Construction monitoring of steel truss highway and railway bridge deck strengthing process[J].Construction Quality, 2014, 62(11): 121-126 .

[13]艾军, 史丽远. 公路梁桥体外预应力加固设计与施工方法研究[J]. 东南大学学报: 自然科学版, 2002, 32(5): 771-774.

[14]江祥林, 易汉斌, 俞博. 体外预应力加固桥梁技术与工程实例[J]. 岩土力学, 2013(3): 912-912.

[15]HINDI A N, KREGER M E, Breen J E. Enhancing the strength and ductility of post-tensioned segmental box-girder bridges[J].Mathematical Models, 1991, 76(4): 378-383.

(责任编校：徐赞)

Flexible Failure Experimental Study and Numerical Simulation on the Prestressed Concrete Box-girder

PENG Hui, XIE Jun-wu
(Hunan Chengjiao Design & Research Institute Co., Ltd, Changsha, Hunan, 410114, China)

The external prestressed tendons are widely used in the construction of the new bridge and the reinforcement of the old bridge. The construction method is more mature, but the specific force of the construction method is not analyzed deeply, and its root is the influence of the external load The lower structure and the prestressed tendons will produce relative movement, the existing theorem of the deformation coordination assumption can not accurately reflect the actual situation. Based on the assumptions of the Euler-Bemoulli theory and the actual deformation of the external prestressing tendons, the theory of prestressed prestressing in the bridge is improved, it has certain reference value for the engineering design.

prestressing method; bridge reinforcement; external prestressing

U442

A

10.3969/j.issn.1672-7304.2017.03.0005

1672–7304(2017)03–00021–04

2017-05-06

彭辉(1984-)，男，湖南慈利人，工程师，主要从事桥梁工程研究﹒E-mail: 50627552@qq.com.