海洋水文观测数据聚类

闫 可 程文芳

1(复旦大学计算机科学技术学院 上海 201203) 2(中国极地研究中心 上海 200136)

海洋水文观测数据聚类

闫 可1程文芳2

1(复旦大学计算机科学技术学院 上海 201203)2(中国极地研究中心 上海 200136)

在科学考察中，数据的获取受自然环境因素以及监测成本影响较大，实际布放的监测点的数量和位置可能无法达到预期，并且所采集的数据集中通常包含了多种监测要素，利用数据分析来弥补因自然环境影响而造成的数据缺失并找出数据变化规律显得尤为重要。以南极普里兹湾水文数据为研究对象，利用空间插值的方法，来弥补数据不足和监测点稀疏的问题，再将改进的动态时间弯曲距离算法用于具有多要素特性的水文深度序列相似度衡量，实验结果表明相较于传统的欧氏距离相似度衡量更为准确。基于所提出的相似度衡量算法，对普里兹湾水文数据进行聚类，并获得了每个簇的空间分布情况。

水文数据 空间插值 动态时间弯曲 相似度衡量 深度序列 K-means

0 引 言

科学数据挖掘定义为：将数据挖掘应用于科学问题，而不是商业、经济等领域，相对于传统的商业数据驱动的数据挖掘应用主要的区别在于数据集的性质，不仅仅是数据本身的性质还包括数据获取以及处理的过程也有显著的不同。科学数据是科研人员为了研究某一类学科或者特殊现象而采集的一系列数据集，例如气象现象、土壤性质、种群迁徙等[1]。通常包含了多种监测要素，且要素之间相互影响，如何在包含有多种要素的数据集中挖掘出潜在的规律是一大挑战；另外实地科学考察对于科学数据的获取有重要意义，然而在实际的监测点选取以及设备布放的过程中，可能受到地形、地貌、气候环境以及监测成本等因素影响，从而导致这些监测点通常在空间上的分布是非常稀疏的且不规则，在对这些数据进行数据分析之前需要对其进行预处理来弥补这种数据缺陷。本文以考察环境极为恶劣的南极普里兹湾海域的水文数据为研究对象。论文主要工作包括：利用空间插值对实际采样点所采集数据进行插值，解决数据不足以及站点分布稀疏的问题；再将动态时间弯曲的思想用于水文深度序列的相似性衡量中，并加以改进；基于上述序列相似度衡量算法对经过插值后的水文深度序列进行聚类。

1 南极普里兹湾水文数据

自1984年我国首次对南极附近海域展开调查以来，迄今已经完成了32次南极科考，获取了大量的水文、气象、生物、化学、地球物理、地质、地磁等多个学科的观测资料。目前在雪龙船上配备有SBE911-CTD设备，用于收集在各个站位的水文调查数据，其中所采集的数据规范到1 m一个记录，采集的要素有：不同深度下的温度、盐度、密度、声速等。水文观测方式为，雪龙船航行至指定站位停船，将所携带的CTD设备抛入海中，完成不同深度的下的数据采集，实现一定深度范围内的水文监测要素剖面观测。由于南极气候条件恶劣以及监测成本的限制，无法对该区域进行密集的数据采样，导致了的实际数据监测点分布稀疏的问题，如图1是第29次南极科考普里兹湾海域的站位分布情况，共计62个监测站位，图2是10 m水深的盐度散点图，每个站位可监测不同深度下的水文数据。从图1中可以直观的看出，监测站位分布比较稀疏。

图1 第29次南极科考普里兹湾站位分布

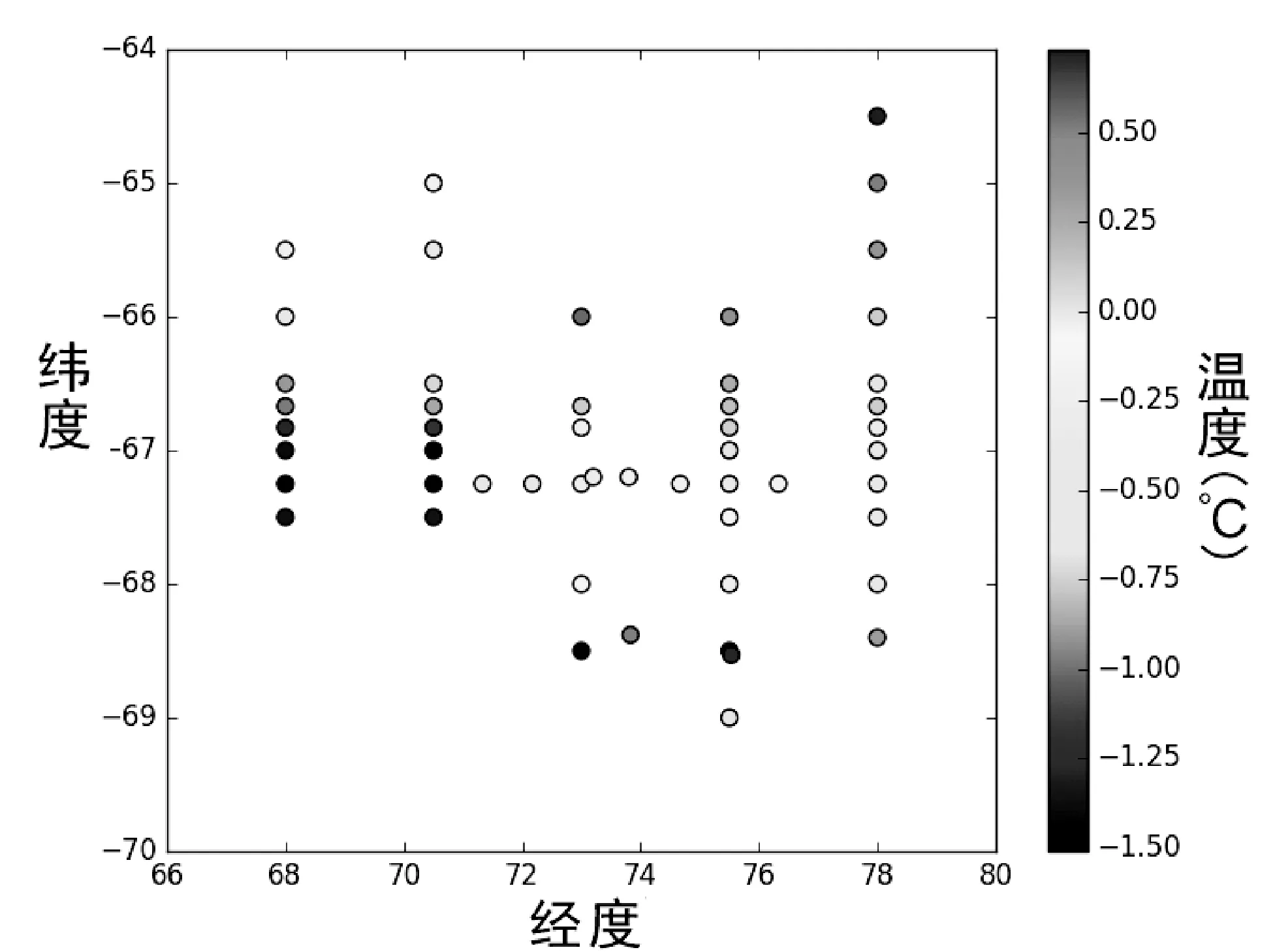
图2 第29次南极科考普里兹湾10 m水深的盐度散点图

2 水文数据空间插值

为了弥补监测站位稀疏的缺陷，我们引入了空间插值的方法。首先将整个普里兹湾区域等分成更小的区域，每个小块区域的水文数据均可由空间插值方法获得。将每个小区域看成一个监测点，可以得到监测点分布非常密集的水文数据。最后对这些水文数据进行聚类，可以将水文数据属于同一类的小块划到同一块区域中。如图3，可以直观地看出水文数据变化特征的空间分布。当然这些小区域越小，我们的普里兹湾区域划分的最终结果也就越精确。

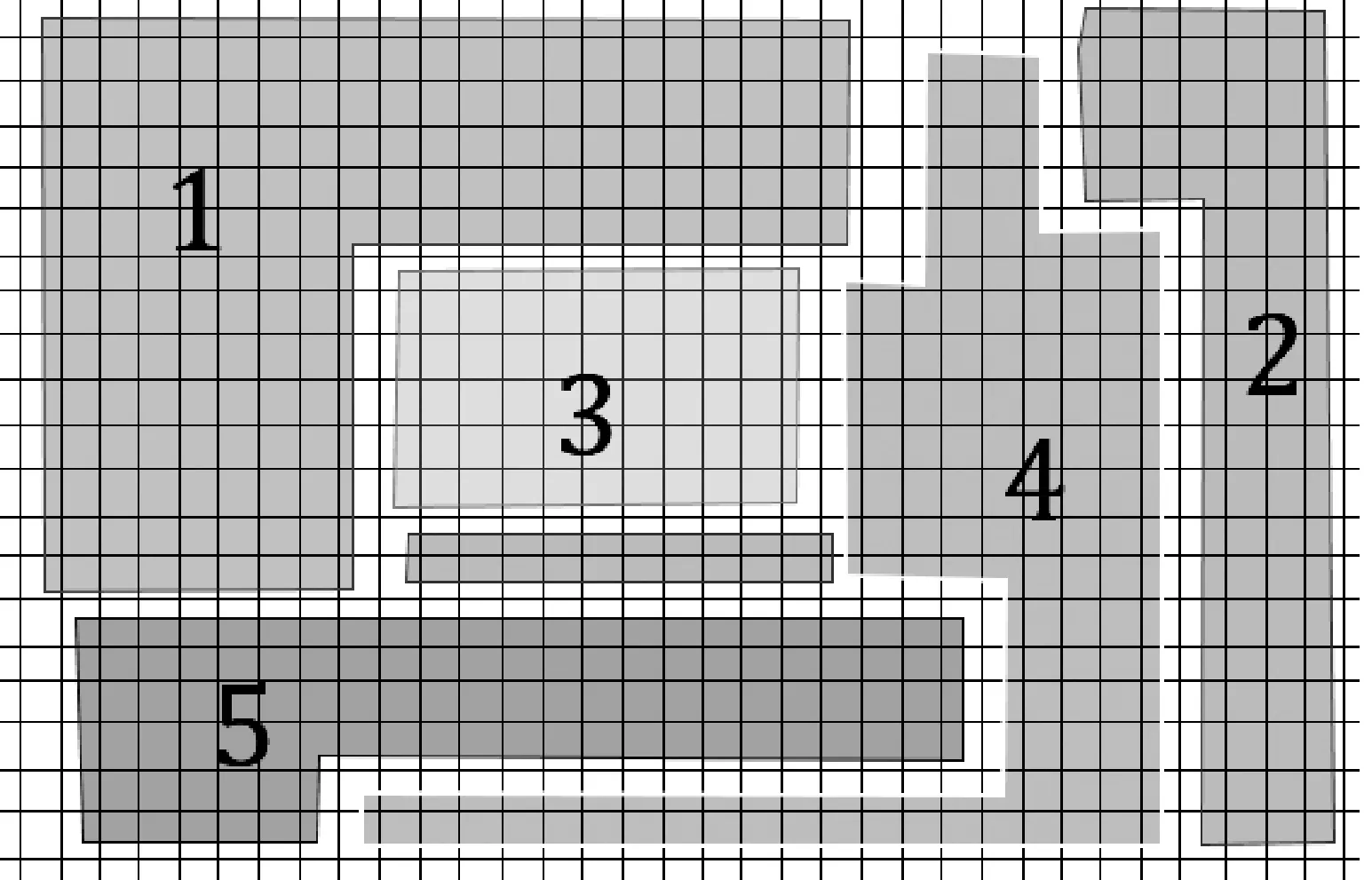
图3 区域划分效果图

2.1 空间插值算法

目前已经有许多空间插值的方法用于已有数据来估计非采样点的值，将不规则分布的数据处理为规则分布的数据，将空间插值的方法应用到科学数据挖掘中是科学数据集预处理过程重要的一步[2-4]。

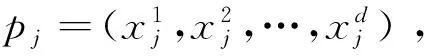
反距离加权是最简单的插值方法之一。 它基于这样的假设，即非采样点处的值可以近似为在特定距离内的采样点或给定数量的最近的采样的点值的加权平均值，权重通常与距离的幂成反比。

最近邻插值同样是一种简单的插值算法，它只考虑离未知点最近的已知点的影响，而不考虑其他相邻点的影响，该方法基于由一系列空间离散点绘制的沃罗诺伊图(Voronoi Diagram)来实现。

克里金插值是最典型的利用地统计学的插值方法，基于随机函数的概念：区域内的值被假定为具有特定空间协方差的随机函数的函数值。克里金改进了反距离加权插值中权值的计算，它的权值是能够使得该点的估计值和真实值的差最小的一系列系数。

样条插值是典型的基于分段拟合的插值算法，给定一个离散函数fk=f(xk)，k=0,1，…,N，样条其实是在每对离散点之间的多项式函数，保证内插函数在全局平滑度上保证在某阶可导。最简单的样条插值为线性样条，即在特定区间[xk,xk+1]，插值公式为一个线性函数；三次样条插值是常用的样条插值，它的目的是得到一个二阶可导且二阶导连续的函数。

2.2 插值算法选取

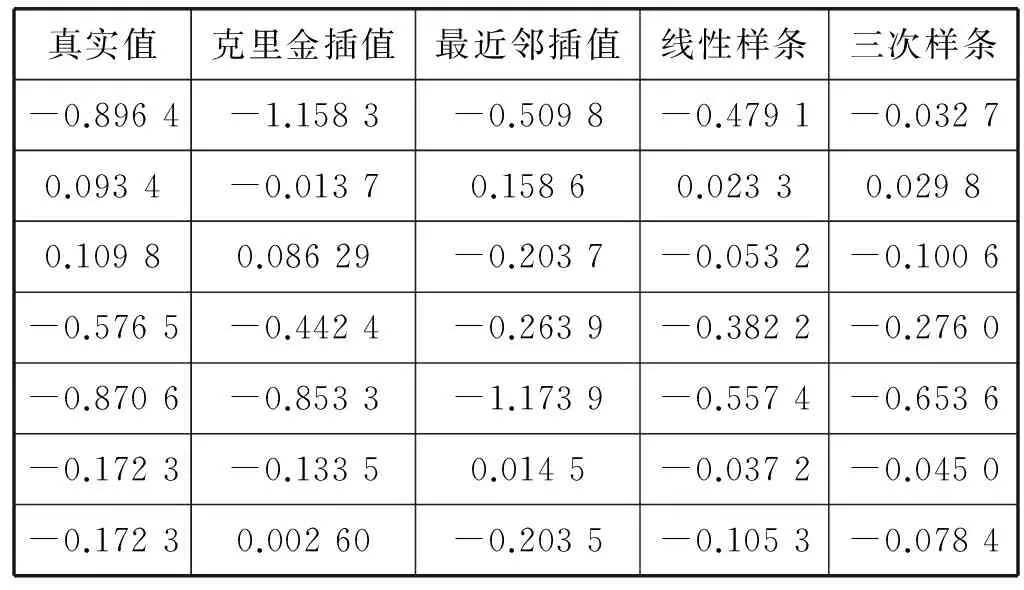
选取常用的空间插值算法：最近邻插值、克里金插值、线性样条插值以及三次样条插值。第29次南极科考普里兹湾海域共有监测点62个，选取其中的55个监测点10 m水深处温度数据利用上述插值算法分别进行插值，如图4所示。用其余的7个点作为测试点，用于比较各插值算法之间的误差大小。结果如表1所示。

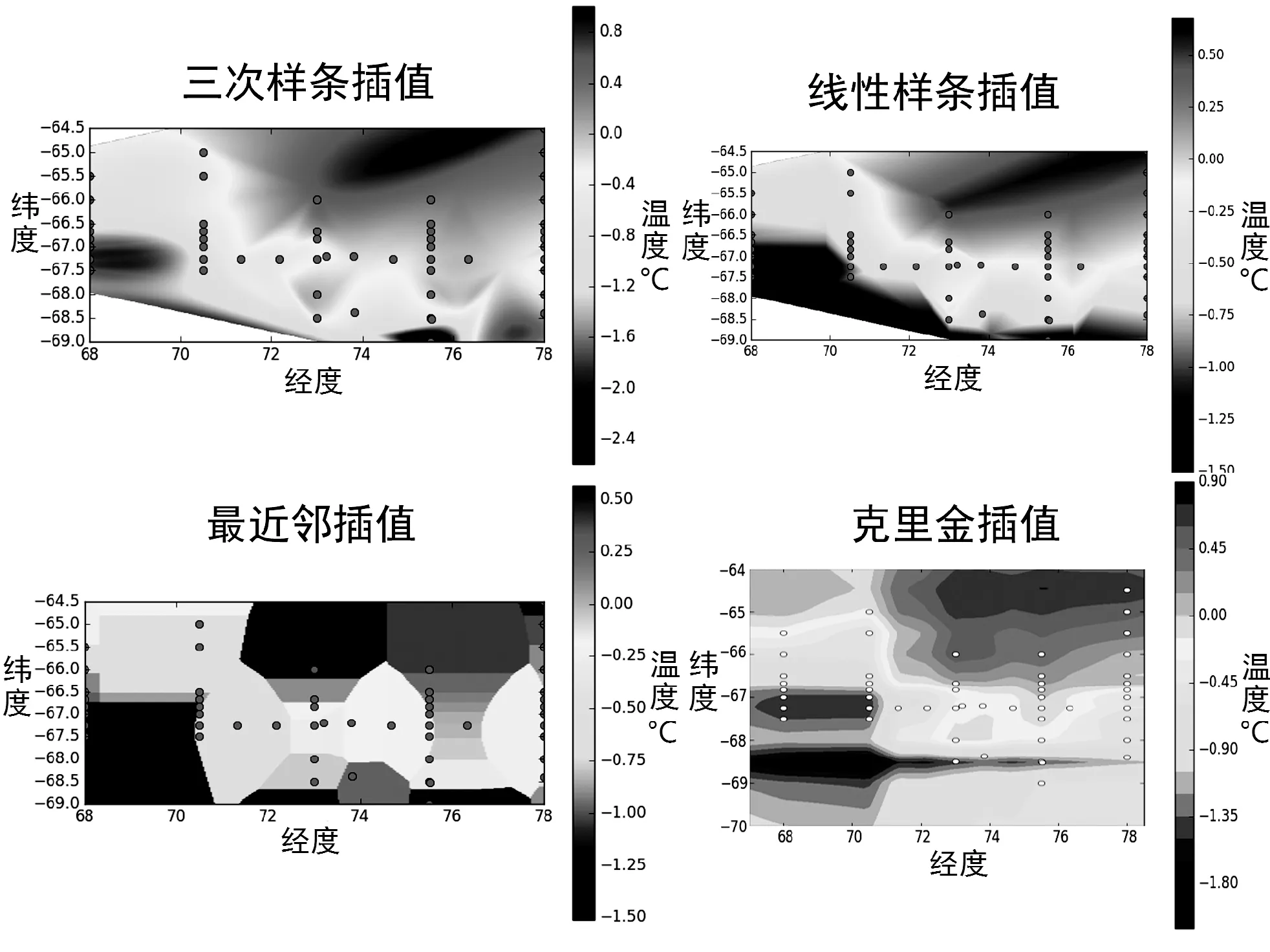
图4 插值结果

真实值克里金插值最近邻插值线性样条三次样条-0.8964-1.1583-0.5098-0.4791-0.03270.0934-0.01370.15860.02330.02980.10980.08629-0.2037-0.0532-0.1006-0.5765-0.4424-0.2639-0.3822-0.2760-0.8706-0.8533-1.1739-0.5574-0.6536-0.1723-0.13350.0145-0.0372-0.0450-0.17230.00260-0.2035-0.1053-0.0784

最终得到这4种插值算法在这7个测试点估计值与真实值得平均误差，其中平均误差最小的是克里金插值算法为0.108 23 ℃。我们选取误差最小的克里金插值法，对温度和盐度数据进行插值，综合这两类水文监测要素的变化序列从而得到普里兹湾任意一点的水文变化深度序列，如图5是仅包含有温度和盐度两个要素的深度序列。

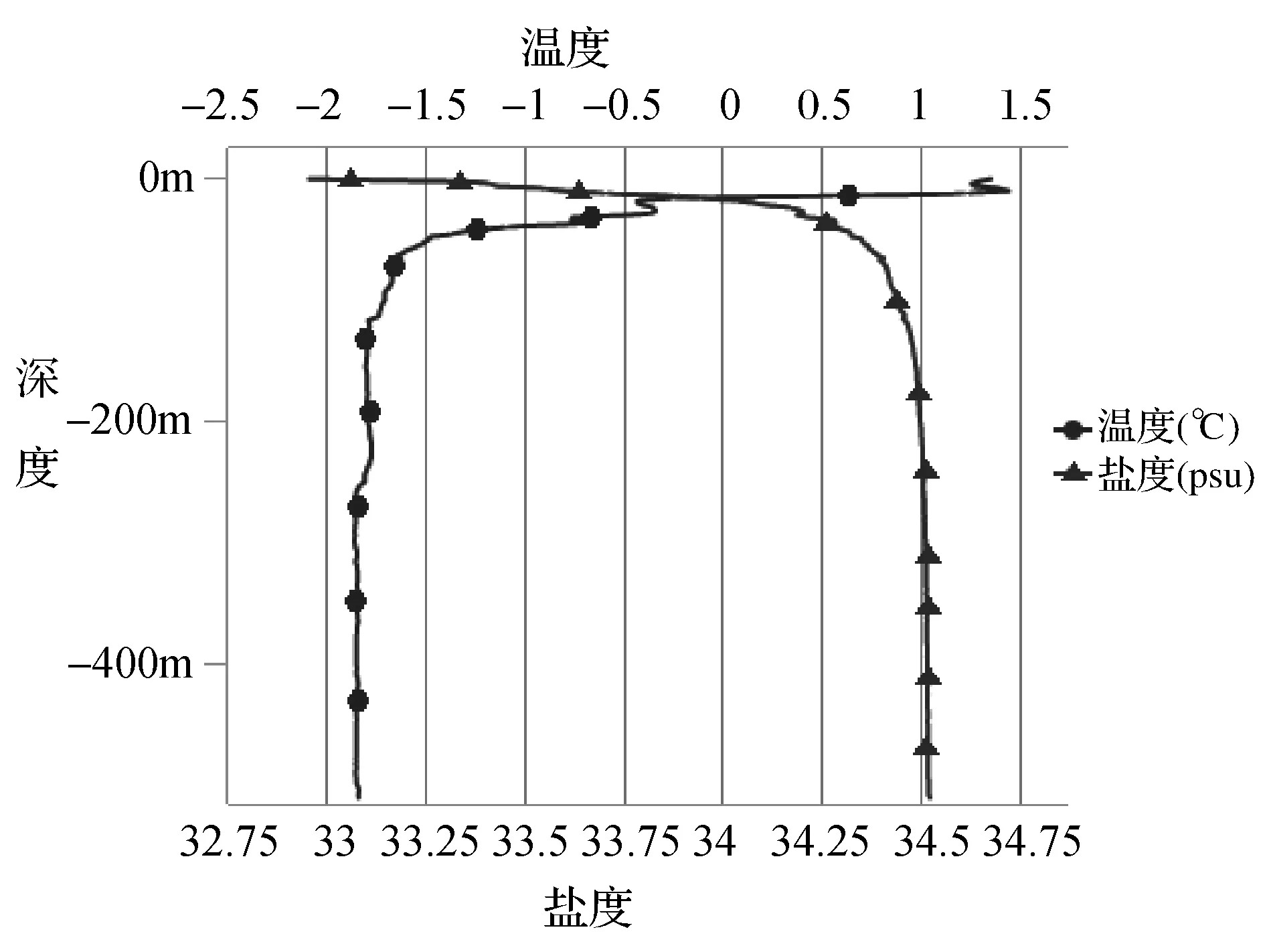
图5 温盐深度序列

由此可以得到我们之前划分的小块区域的温盐深度变化序列。由于我们要对这些序列进行聚类，为了消除量纲对聚类算法中距离计算的影响，需要对温盐深度序列进行归一化处理，将数值变为[0,1]内的小数，采用线性函数转换如公式：

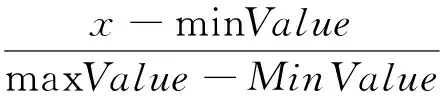
(1)

其中x、y分别表示变换前的值和变换后的值，MinValue、MaxValue分别表示数据的最小值和最大值。

考虑到时间序列与深度序列之间的相似性，接下来重点介绍处理后的水文数据聚类。我们将动态时间弯曲距离计算的思想应用到普里兹湾水文序列的相似度衡量，由于水文数据涉及到多种要素，我们对动态时间弯曲距离公式进行改进，以适用于水文序列相似度的衡量。

3 改进动态时间弯曲算法

动态时间弯曲DTW(Dynamic Time Warping)距离是基于序列形状相似性计算的方法。DTW通过使用动态规划的思想来发现所有可能的弯曲路径，从而在两个时间序列中选择最小的距离。也就是在两个序列中找出最优对齐的方案，也可以理解为两个序列在时间方向上进行扭曲以彼此匹配[5-6]。假设有两个序列Q(q1,…,qi,…,qn)和C(c1,…,ci,…,cn) ，由于我们通过插值得到的深度序列长度均是相同的，所以这里假设Q的长度和C的长度相同均为n。首先创建一个n×n的距离矩阵，这里定义矩阵元素(i,j)的值如公式：

(2)

其中1≤i,j≤n，di,j=(ci-qj)2，DTWi,j是di,j与(i,j)元素周围的三个元素的最小累积距离的和，然后通过找出最优路径，定义两个序列在(n,n)最小的累计距离如公式:

其中P是所有可能的弯曲路径，wk是弯曲路径第k个点(i,j) 的值，K是弯曲路径的长度。表示序列Q和C映射关系的一条弯曲路径，如图6所示。

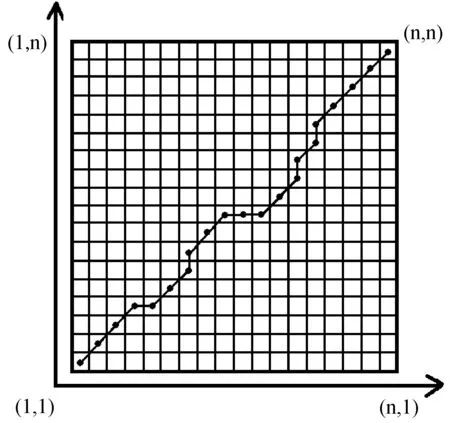
图6 弯曲路径

深度变化序列和时间序列在相似性衡量上有相似之处，只是要素值不是随时间的变化而变化，而是随深度的变化而变化，如果采用传统的欧式距离的方法来衡量两个深度序列之间的相似性是不合理的。对于普里兹湾水文数据，当雪龙船航行至指定的站位时停船，抛下水文监测仪器，以此来采样该监测站位的水文数据，采集完成后再航行至下一个站位，这样的数据采集方式带来了两个显著的问题：

1) 不同站位的数据均是在不同的时刻采集的，站位在航线上位置相距越大，采样的时间间隔也就越大，水位会随着时间的推移而变化，由于水位的变化而导致了两个站位同一深度的数据可比性减弱。

2) 由于实际作业条件限制，导致了采样仪器在各个站位的下沉过程速度通常不同。因为采样间隔为1 m，如果仪器下沉速度过快会导致采样层的海水收到了来自上层海水的干扰，从而导致实际数据在深度轴上会产生一定偏移。

在时间序列相似性比较中，由于传统欧式距离对数据在时间轴上的偏移较为敏感，一些轻微的数据偏移都会导致两个序列之间的欧式距离变得很大。因为欧式距离的计算时必须要保证序列的每个点一一对应，正如之前所提到的普里兹湾水文数据所存在的实际问题，直接利用欧式距离来衡量两个深度序列的相似性是不合理的，而动态时间弯曲距离可以有效地弥补欧式距离的这一缺陷。一方面，由水文深度序列与时间序列的相似性，我们利用动态时间弯曲算法来计算深度序列之间的最短距离，以此来衡量序列之间的相似度；另一方面，DTW仅适用于单个参数的时间序列，而本文研究的普里兹湾水文深度序列涉及到多个要素，即在相同的深度下会采集温度、盐度、密度等多个水文参数值。

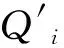
(4)

但是这样做最大的缺陷是忽略了水文要素之间的关系，所以这里需要调整传统DTW中的距离公式d。如图7所示，向量a与c的欧式距离向量a与向量b的欧式距离均为d，但是它们的向量夹角却不相同，可以很明显看出α>β，尽管向量b、c与a的欧式距离相等，但是由于a与c的夹角更小，我们认为c与a更相似。

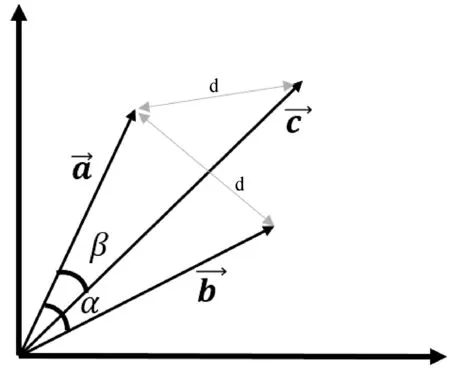
图7 向量相似度比较

基于上述观点，我们重新定义两个多维向量的距离如公式：

(5)

其中cosα的计算如公式:

(6)

当然在实际使用过程中，DTW或许不能根据我们的需求来给出最好的映射，因为它仅仅是为了找出两个序列的最小距离，可能会得到我们不想要的结果。为此我们需要进行一个全局的约束来限制弯曲路径的选择，Sakoe-Chiba band是最常用的具有全局限制的DTW算法[7-8]。

Sakoe-Chiba band全局约束如图8，宽度通常设置为时间序列长度的10%，但10%的限制对于实际的数据是很大的，尤其是针对本文中提到的普里兹湾海域水文深度序列的聚类。水文数据对深度是十分敏感的，如果深度相差太多即使距离最短也没有实际意义，这里我们也需要对改进DTW算法进行一定限制。目前温盐深度序列的深度间隔为1 m，考虑到实际的水温变化规律，规定约束宽度设置为深度序列长度的4%即20 m范围内，采用对匹配路径约束之后，由于减少了弯曲路径的范围和计算次数，聚类时间也随之减少。

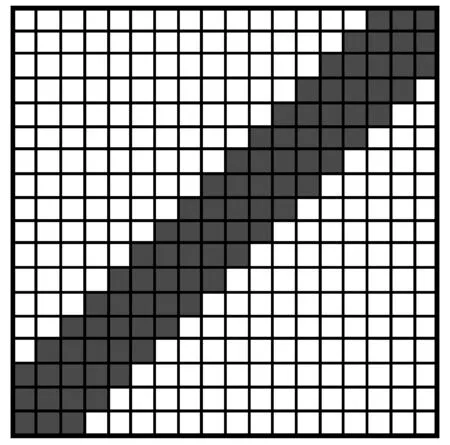
图8 Sakoe-Chiba band

为了衡量算法的有效性，我们将本文提出的深度序列距离公式与传统的欧式距离作对比。对第29次南极普里兹湾温度和盐度进行空间插值之后，我们可以获得任意一点的温盐深度序列。根据空间插值位置相近属性也就相近的基本准则，有如下原则：如果选取插值范围的任意位置的一个点作为中心点，那么离该中心点最近的点的温盐深度序列与中心点的温盐序列最为相似，即可看作属于同一类。基于上述的原则，我们分别选取多个点作为中心点，且保证这些点之间足够分散，以每个中心点的数据作为一类，以每个中心点周围的8个方向上最近的点作为测试点，期望对这些测试点分类后将被划分到它们各自中心点的类中。如果被分到了别的类则视为错误的分类，实验结果如表2所示。本文方法与传统欧氏距离的正确率比较如图9所示。可以直观地看出，本文所提出的水文深度序列相似度衡量方法的准确性相对于以欧氏距离衡量相似度的方法更为准确。

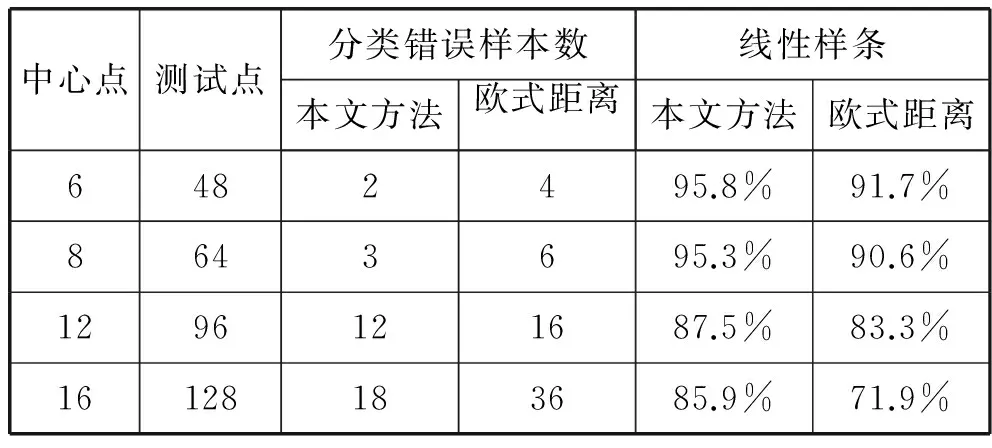
表2 两种方法分类实验结果比较

图9 算法准确率

4 普里兹湾水文数据聚类

考虑到温度和盐度时普里兹湾水文数据中相对比较重要的物理量，接下来我们对仅包含温度和盐度要素的深度序列进行聚类。数据采用第29次南极科考期间普利兹湾海域所采集的水文观测数据，监测站位共62个，站位东西跨度为68°E至78°E，南北跨度为64.5°W至69.16°W，考虑到保证插值结果的准确性，将插值方位限制在经度68°E至78°E，纬度64.5°S至69°S。考虑到实际测量过程中，表层海水受气候环境因素影响较大，将每个站位的温盐数据深度范围限制在10 m至500 m，深度间隔为1 m。我们将所选定的区域进行细分，划分为经纬跨度均为0.125°的小块，共计2 880块，将以该小块中心的温盐变化代表整个小块的温盐变化。

整个数据预处理过程分为两个部分。一是利用克里金插值算法将每隔1 m水深的温度和盐度分别进行插值，获得密集且空间上规则分布的数据集，共2 880条温盐深度序列，且每条序列长度为491，其中最高温度1.12 ℃，最低温度-2.42 ℃，最大盐度值34.70 psu，最低盐度值32.45 psu。二是基于本文所提出的水文深度序列相似度衡量算法，利用K-means聚类算法将处理后的所有温盐深度序列进行聚类，最终将2 880条数据划分成了6个簇，其中每个簇的中心序列如图10所示，每个簇的空间分布情况如图11所示。

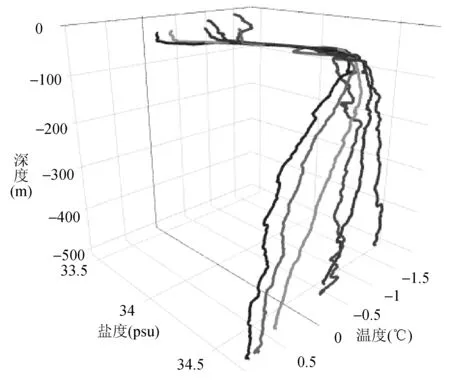
图10 聚类结果

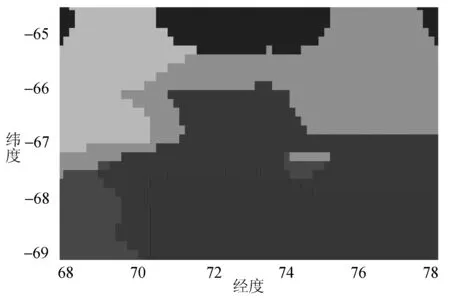
图11 类空间分布

5 结 语

水文数据的采集往往受环境因素影响，尤其是在极地环境。由于资源有限，外加采样环境极其恶劣，实际监测站位的选取往往较为稀疏且分布不规律。而且由于水文数据的特殊性，传统的相似度衡量算法不再适用，对数据缺失的水文数据聚类是一项巨大的挑战。在本文中，首先对已有数据进行预处理，预处理过程包括每一层深度下的数据进行插值，得到普里兹湾任意一点的水文深度序列。之后基于本文所提出的水文序列相似度衡量算法，利用K-means聚类算法实现对南极普里兹湾海域所有水文深度序列聚类，从而获得多个类簇。利用各个序列的空间位置信息，可以直观地看出每个簇的空间分布情况，为今后的科学研究提供一定的参考价值。下一步工作方向为进一步优化水文深度序列相似度衡量算法，提高算法效率，减少聚类时间。

[1] Embrechts M J, Szymanski B, Sternickel K. Introduction to Scientific Data Mining: Direct Kernel Methods and Applications[M]//Computationally Intelligent Hybrid Systems: The Fusion of Soft Computing and Hard Computing. John Wiley & Sons, Inc. 2005:317-362.

[2] Bello A, Reneses J, Muoz A, et al. Probabilistic forecasting of hourly electricity prices in the medium-term using spatial interpolation techniques[J]. International Journal of Forecasting, 2016, 32(3):966-980.

[3] Bradley J R, Cressie N, Shi T. A comparison of spatial predictors when datasets could be very large[J]. arXiv preprint arXiv:1410.7748,2014.

[4] Li J, Heap A D. Spatial interpolation methods applied in the environmental sciences[J]. Environmental Modelling & Software, 2014, 53(C):173-189.

[5] Kate R J. Using dynamic time warping distances as features for improved time series classification[J]. Data Mining and Knowledge Discovery, 2016, 30(2):1-30.

[6] Shokoohi-Yekta M, Hu B, Jin H, et al. Generalizing DTW to the multi-dimensional case requires an adaptive approach[J]. Data Mining & Knowledge Discovery, 2017,31(1):1-31.

[7] Niennattrakul V, Ratanamahatana C A. Learning DTW Global Constraint for Time Series Classification[J]. Computer Science, 2009.

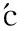
CLUSTERINGOFMARINEHYDROLOGICALOBSERVATIONDATA

Yan Ke1Cheng Wenfang2

1(SchoolofComputerScience,FudanUniversity,Shanghai201203,China)2(PolarResearchInstituteofChina,Shanghai200136,China)

In the course of scientific investigation, the acquisition of data is greatly affected by the natural environment factors and the monitoring cost. The actual number and location of monitoring points may not be able to meet the expectations and the collected data set usually contains a variety of monitoring elements. It is particularly important to use data analysis to compensate for lack of data caused by the natural environment and find out the law of data change. Based on the hydrological data of Prydz Bay in Antarctica, the use of spatial interpolation method to make up lack of data and sparse monitoring points, then the improved Dynamic time warping distance algorithm is applied to the similarity measure of hydrological depth series with multi-element. The experimental results show that similarity measurement algorithm is more accurate than the traditional Euclidean distance. Based on the similarity measurement proposed in this paper, the Prydz Bay hydrological data are clustered and the spatial distribution of each cluster is obtained.

Hydrological data Spatial interpolation Dynamic time warping Similarity measure Depth sequence K-means

2016-12-26。极地海洋环境监测网系统研发及应用示范项目(201405031)。闫可，硕士生，主研领域：软件工程。程文芳，高工。

TP391

A

10.3969/j.issn.1000-386x.2017.11.007