初中数学数形结合教学要点探究

唐永莲

摘 要：随着社会的不断进步和经济的快速发展，人们的物质生活水平不断提高，教育教学也变得越来越重要。初中数学作为一门基础性学科，数形结合可以把代数问题几何化，几何问题代数化，从而帮助初中生更好地学习数学。

关键词：初中数学；数形结合；教学要点

数形结合作为数学研究过程中的一种重要思想方法，在初中数学教学中加以应用，能够很好地培养学生的创新能力，帮助学生形成数形结合的思维方式，进而为学生的自主学习和发展奠定坚实的基础。对初中数学数形结合教学要点进行了分析与探讨。

一、代数教学中数形结合思想的应用

从初中一年级开始，实数逐渐走进学生的视野，其中以有理数的学习为主体。在有理数的学习中，经常用数轴来表示数，这个过程就已经用到了数形结合思想。可以这样说，对于每一个实数，在数轴上都有唯一确定的点与之对应。因此，比较两个实数的大小，就可以通过这两个数在数轴上对应点的位置关系反映出来。与实数大小比较类似，相反数、绝对值是数轴上的点通过与原点的位置关系定义的。尽管我们教给学生的是（实）数，但不能忽略它的形，也就是与数轴的关系。下面举一个简单的例子来说明。

例1.如图1所示，在数轴上有A，B两点分别对应实数a，b，下列正确的是（ ）

A.|a|>|b| B.a+b>0 C.ab<0 D.|b|=b

分析：观察A、B在数轴上的关系，不难得到以下结论，b<0，a>0，且b<-1，a<1，进一步可得，a+b<0，所以B项错误；B离原点的距离比A离原点的距离远，因此|b|>|a|，所以A项错误；A、B两点分别在原点两侧，因此ab<0，所以C项正确；B点在原点左侧，绝对值等于其相反数，也就是|b|=-b，所以D项错误。故选择C

选项。

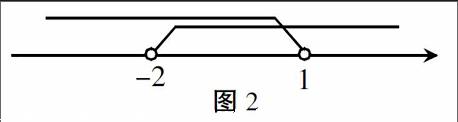
当然，不等式教学也离不开数形结合思想的渗透，比如求解不等式组2（x+2）2x ② ，解不等式①得x<1，解不等式②得x>-2，通过在数轴上分别表示出不等式①、②的解集（如图2），不难得出原不等式组的解集为-2

二、几何教学中数形结合思想的应用

在几何教学中，为了使得所有学生都能学好几何知识，教师应该给学生渗透数形结合的思想。通过数的精确性以及严密性精确表明形的一些属性，使几何问题代数化。

例2.如图3，半圆O上有A，D，G，M四点，四边形ABOC，DEOF，HMNO均为矩形，设BC=a，EF=b，NH=c，则下列说法哪项是正确的（ ）

A.a>b>c B.a=b=c C.c>a>b D.b>c>a

此题用数的方法难以下手，不妨考虑數形结合的方法，先做出一个半圆，然后分别作出矩形ABOC，DEOF，HMNO，因为BC=OA，EF=OD，NH=OM，而OA，OD，OM都为圆的半径，所以线段BC=EF=NH，即a=b=c，选择B选项。

三、概念教学中数形结合思想的应用

要想真正学好数学，就必须彻彻底底吃透数学概念，把握概念核心本质。数学概念是建立数学定理、法则、公式的基础，同时也是数形结合思想方法的出发点，它反映了事物在数量关系和空间形式方面的本质属性。初中数学数形结合教学过程中，教师一定要深入分析数学概念，引导学生找出事物之间的共同本质属性，让学生通过数形结合相互转化，体会数学思想和方法。

例如，在讲解圆与圆之间的位置关系时，教材上只有文字性的叙述，学生理解起来比较困难，如果引入数形结合思想就可以很好地解决这个问题。设圆心距为d，两圆的半径分别为R，r（R>r），那么圆与圆之间的位置关系就可以用图4明确表现出来。

综上所述，数形结合思想方法对于学生学好数学起着至关重要的作用，初中数学教师应该结合学生实际生活情况，潜移默化地给学生渗透数形结合的思想方法，让学生在解决实际问题时能够有效应用数形结合思想方法，养成良好的学习习惯，从而有效提升学生的数学学习能力。

参考文献：

[1]肖前英，刘志杰.数形结合思想在初中数学教学中的渗透探究[J].教育，2015（42）：27.

[2]章南海.“数形结合”思想在初中数学教学中的渗透探究[J].读写算（素质教育论坛），2014（21）：43-44.

编辑 赵飞飞