GA-BP神经网络在钢铁加热炉建模中的应用*

薛美盛 杨 猛 刘 波 孟 俊

(中国科学技术大学信息科学技术学院)

GA-BP神经网络在钢铁加热炉建模中的应用*

薛美盛 杨 猛 刘 波 孟 俊

(中国科学技术大学信息科学技术学院)

基于现场采集的大量的数据，采用BP神经网络建立现场加热炉炉温的非线性模型，并提出利用遗传算法优化BP神经网络的参数与阈值，有效避免了BP神经网络易陷入局部最小值、收敛速度慢的不足。仿真结果表明：在同样的数据集下，GA-BP神经网络的稳定性更好，预测精度更高。

GA-BP神经网络 加热炉 非线性建模 优化

对于钢铁加热炉的控制，通常认为控制对象在整个控制过程或某一阶段是线性的，通过相对成熟的线性系统设计方法实现辨识和控制[1，2]。然而在工业过程中，线性系统只是在一定范围内对非线性系统的简单近似。随着对加热炉控制精度要求的提高，如果再利用此方法进行分析和控制，就很难达到精确控制的目的[3]。

近年来，随着人工智能的不断发展，智能技术在仿真中的应用越来越多[4，5]，其中人工神经网络(Artificial Neural Network，ANN)和遗传算法(Genetic Algorithm，GA)都是仿生学理论的重要成果，它们将生物学原理巧妙地应用于控制科学的研究中。ANN将人或动物脑神经中的若干基本特征进行抽象和模拟，而GA的原理源于自然界中生物进化的机制[6]。将GA和ANN结合在一起，充分发挥双方的优势，提高两者的适应能力，从而得到一种更加行之有效的方法。

笔者基于某钢铁厂加热炉的现场数据进行建模，将GA与误差反向传播算法(Back Propagation，BP)相结合，优化网络权值，加快了网络收敛速度，避免因为干扰而使网络陷入局部最小值的问题。希望以此为例，验证基于现场数据的智能建模方法的可行性及其优势，为在整个项目中推广加热炉智能建模与控制做铺垫。

1 加热炉系统辨识模型的建立

在加热炉建模过程中，将煤气流量作为神经网络的输入，将加热炉的输出温度作为神经网络的输出，利用神经网络强大的拟合非线性系统能力建立模型来表现加热炉的特性，加热炉系统辨识模型如图1所示。

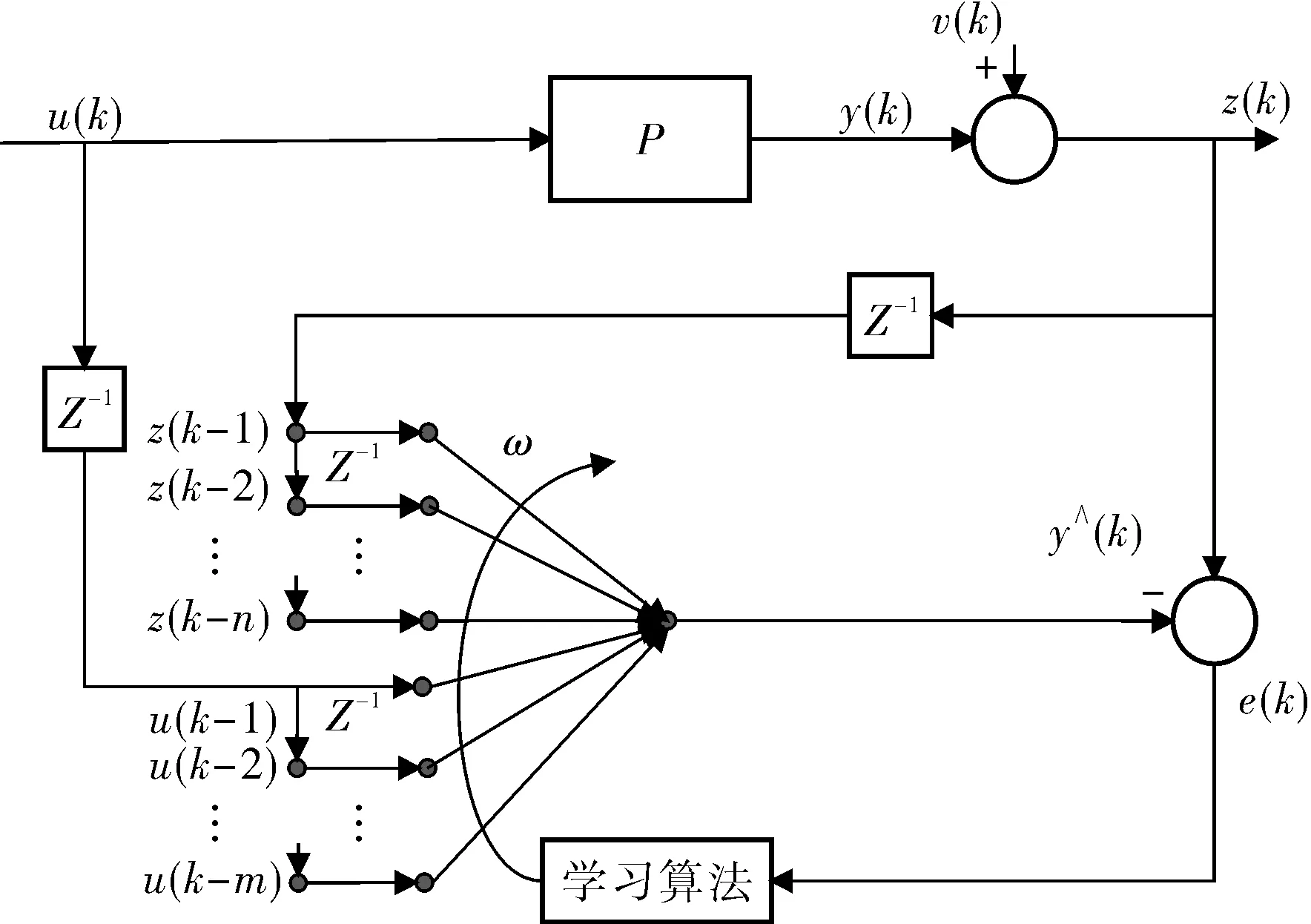
图1 加热炉系统辨识模型

2 基于遗传算法优化的BP算法(GA-BP)

2.1GA-BP原理

BP算法通过计算神经网络的实际输出与期望输出之间的误差，并根据误差的负梯度方向，从后向前逐层迭代修正各层神经元之间的连接权值[7]。三层BP前向神经网络模型如图2所示。

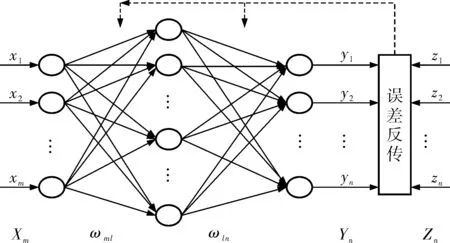
图2 三层BP前向神经网络模型

BP算法是一种梯度下降搜索算法，因此其本身也存在一些不足之处，如易陷入误差函数的局部极小值，并且对于大范围搜索函数、多峰值函数和不可微函数，该算法也不能有效收敛到全局最优值，这导致BP神经网络在实际应用中受到了一定的限制。

GA把自然界“优胜劣汰，适者生存”的生物进化原理，依照所选择的适应度函数，通过模拟生物遗传中的选择、交叉和变异过程对新生个体进行筛选，保留适应度较高的个体，淘汰适应度较低的个体，从而保证新群体既继承了上一代的信息又优于上一代。这样循环反复筛选，直至满足算法中的条件为止[8]。GA之所以能够有效克服BP不足之处的主要原因是它是一种全局优化搜索算法， 从而能够避开局部极小值点。 并且GA在迭代进化过程中不需要计算目标问题的梯度信息，这对训练循环神经网络和不可微传输函数网络具有相当大的潜力，目前的应用范围也在逐渐扩大[9，10]。标准GA算法流程如图3所示。

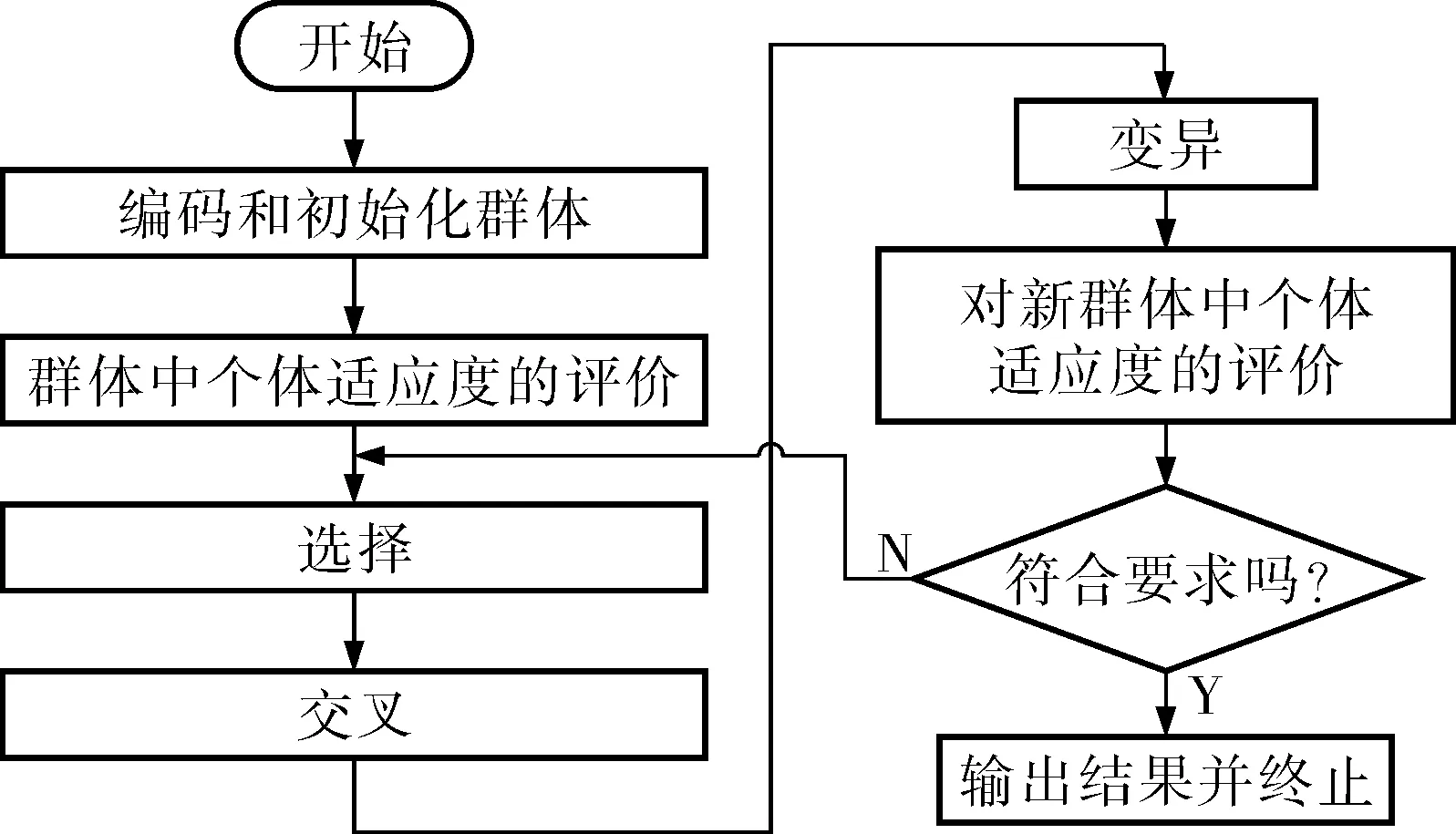
图3 遗传算法优化流程

2.2GA-BP神经网络的设计与实现

GA-BP神经网络的设计流程(图4)为：BP神经网络确定，GA优化和BP神经网络预测。BP神经网络的结构需要依照函数输入输出参数个数和大量的实验与经验确定，从而确定GA中所需个体的长度；GA优化是利用GA对BP神经网络的所有参数进行优化，包括每个神经元的阈值和神经元间的连接权值，每个个体通过适应度函数得到其适应度值，GA通过模拟选择、交叉和变异操作得到最优适应度值所对应的个体；BP神经网络预测是将GA得到的最优个体用于初始化BP神经网络的阈值和连接权值，再经过一系列训练后对函数输出进行预测。

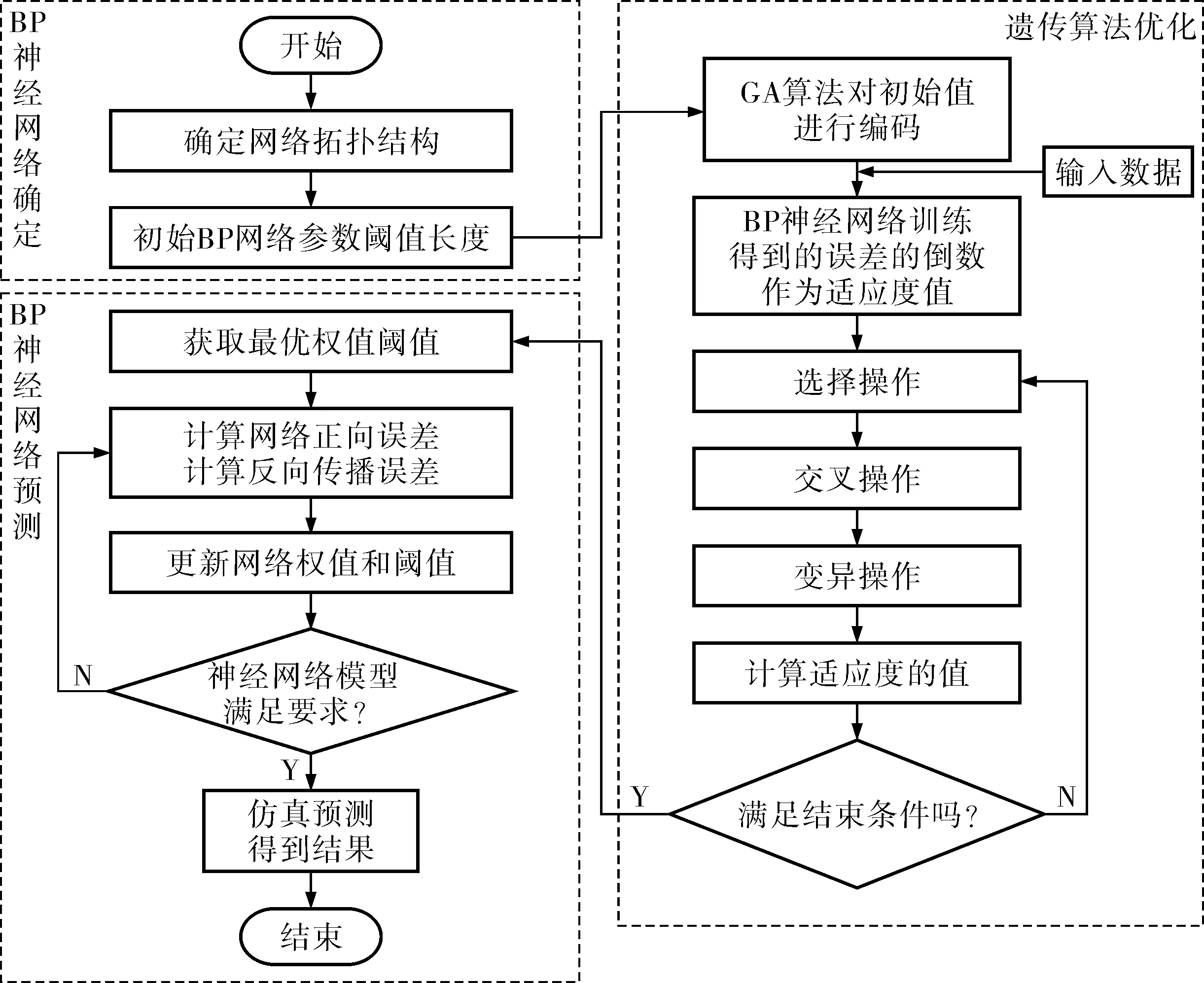
图4 GA-BP神经网络设计流程

固定好BP神经网络的结构后，网络中的参数个数也随之确定，接下来需初始化GA的参数，包括初始化交叉概率、变异概率、种群大小及遗传代数等。遗传操作包含适应度函数选择、选择操作、交叉操作和变异操作。

适应度函数。通过解码种群的每一个个体获得BP神经网络的初始阈值和连接权值，BP神经网络经过训练数据训练后预测系统的输出。选取适应度fi函数值的计算式为：

(1)

式中k—— 比例系数；

n——网络输出节点个数；

yj——网络的第j个节点的实际输出；

zj——网络的第j个节点的期望输出。

个体适应度值越小，该个体越优越。

选择操作。选择基于适应度比例的方法，个体i被选择的概率pi的计算式为：

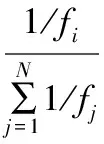
其中，N为遗传算法个体的总个数。

交叉操作。由于个体采用实数编码，因此采用全概率实数交叉，例如：对于两个要交叉的父本P1、P2，采用的交叉方式为：

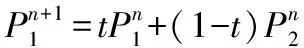
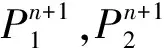
变异操作。第i个个体的第j个基因P进行变异，变异操作方式为：

Pij=Pij+(Pij-Pmax)h(g),r≥0.5
Pij=Pij+(Pmin-Pij)h(g),r<0.5
h(g)=k′(1-g/Gmax)

其中，Pmax代表Pij上界，Pmin代表Pij下界，Gmax代表最大进化次数，g代表当前迭代次数，k′为比例系数，r为[0，1]之间的随机数。

3 GA-BP神经网络的仿真研究

以某钢厂加热炉为研究对象，该加热炉大致分为预热段、一加热段、二加热段和均热段，其中均热段负责将钢温保持在合适的轧钢温度，直接影响下游的轧钢效率和轧钢生产合格率，是加热炉至关重要的部分。目前，现场正在运行的是基于线性辨识的CARIMA模型，但是常出现的工作点漂移现象会导致模型失配，从而难以获得令人满意的炉温控制效果。笔者提出将人工智能引入该项目，通过神经网络建立加热炉的非线性模型取代线性CARIMA模型，以提高模型精度。

笔者采集了2015年10月18日12∶00～24∶00的现场数据来进行非线性建模，采样时间T=30s。通过主成分分析可知，煤气流量是影响温度的主要因素；由相关性分析得知，加热炉的滞后时间为180s；实验以y(k-1)、u(k-6)为输入，y(k)为输出。通过表1可知，当隐层节点个数为6时误差绝对值之和最小，因此，网络采取2-6-1结构，共有18个权值加7个阈值，所以个体编码长度为25、选择终止迭代次数为30、种群规模为20、交叉概率为0.6、变异概率为0.02。从数据集中选择2 000组数据，并从中随机选择1 800组作为训练数据，剩下的200组作为测试数据。个体适应度函数如式(1)所示。不同种群规模和迭代次数对适应度的影响如图5所示，无论初始值如何波动，只要种群达到一定的迭代次数，适应度最终都收敛到26.85左右，因此为了保证GA最终能够达到收敛，种群的终止迭代次数不能太小。将GA得到的参数作为神经网络的初始参数，利用BP算法进行微调，网络参数就能够迅速收敛到全局最优解。训练结束后，利用GA-BP神经网络进行温度预测，结果如图6所示。

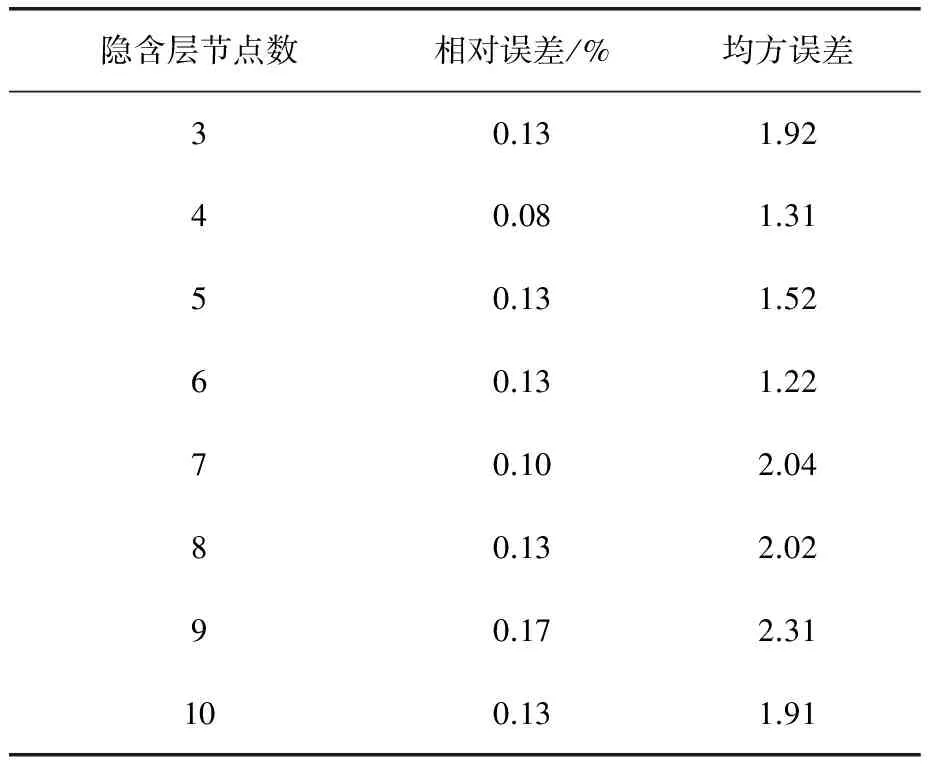
表1 隐层节点个数不同时BP神经网络的预测误差

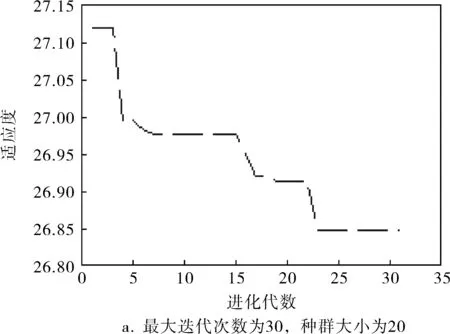
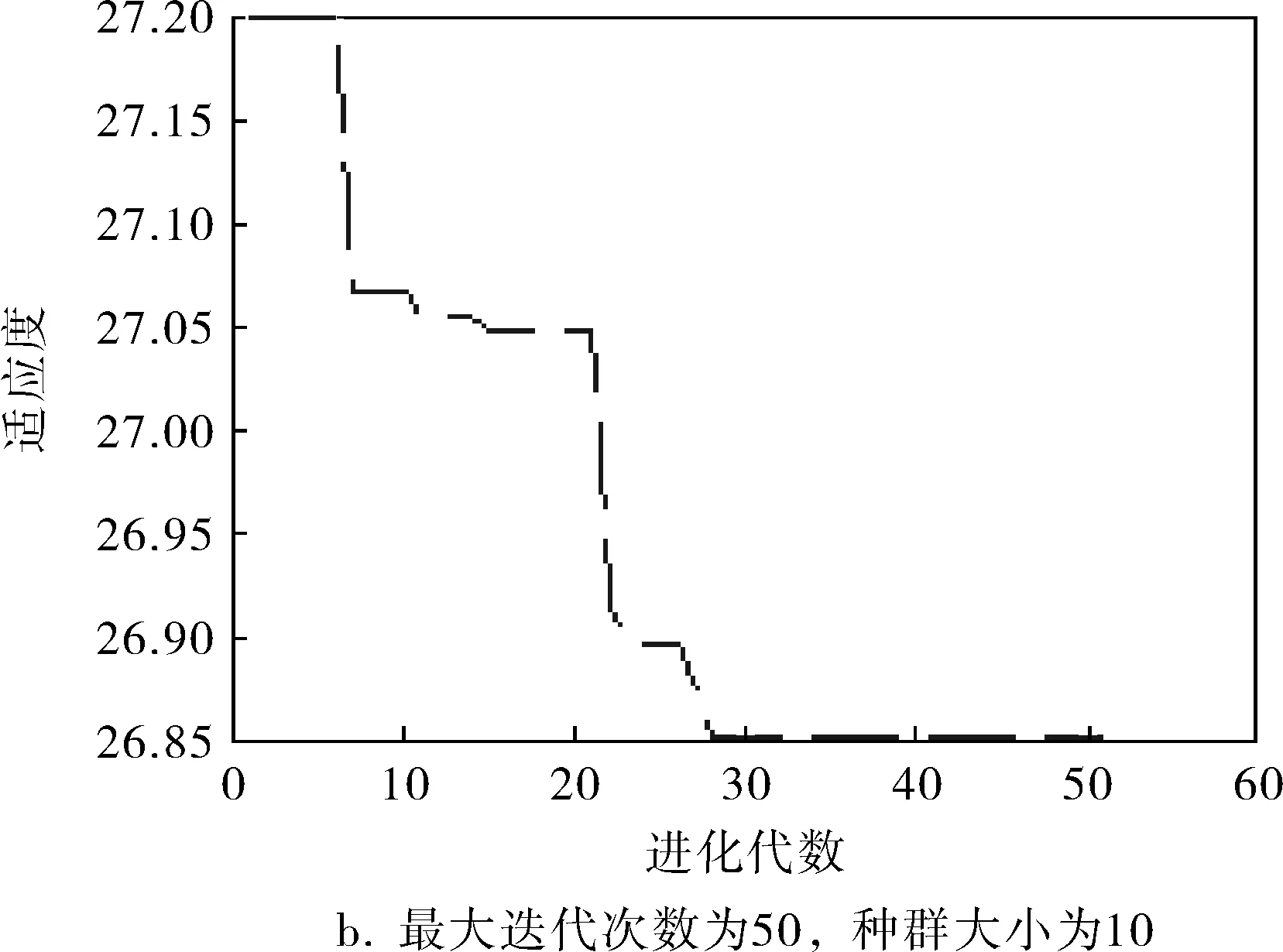
图5 不同种群规模和迭代次数对适应度的影响

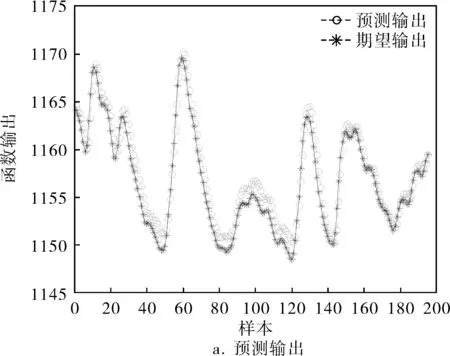
图6 GA-BP神经网络的预测输出与预测误差

作为对比，绘制如图7、8所示的单隐层BP神经网络(2-6-1)、双隐层BP神经网络(2-6-8-1)通过该数据集训练后的预测结果。可以看出，由该炉温样本集提取的神经网络模型中，单隐层BP神经网络的预测误差基本位于[-1，4]之间，在区间[40，60]和[80，120]时，网络的预测误差相对较大；双隐层BP神经网络误差相对较小，其预测误差基本位于[-2，2]之间，但在样本标号为60和130附近时，该网络的预测误差突然增加，导致整个误差分布出现陡峭峰值，其他位置的预测误差相比于单隐层BP神经网络而言差别不大。究其原因，可能是双隐层BP神经网络存在过拟合现象，当预测数据的分布状况与大多数训练数据一致时，预测效果比较精确；反之，当预测数据的分布状况与大多数训练数据分布不一致时，由于过拟合导致网络的泛化性能较差，预测值将严重偏离真实值。然而GA-BP神经网络模型相对于前两者而言，预测精度更高一些，GA-BP神经网络继承了单隐层BP神经网络的优势，泛化性能良好，而且通过GA优化初始值之后，单隐层BP神经网络的权值和阈值迅速收敛到全局最优处。随着BP神经网络越来越复杂，GA的运算量也迅速膨胀，需要的运算时间也会迅速增加。表2为3种网络在预测误差、训练时间、迭代次数方面的对比，可见GA-BP神经网络的优化效果在均方误差、训练次数等方面都是比较满意的，由于GA-BP神经网络的运行时间大部分用于GA算法离线寻优(1 461.04s)，在GA算法寻优结束后，BP算法能够在很短的时间内(3.17s)获得最优权值组合。

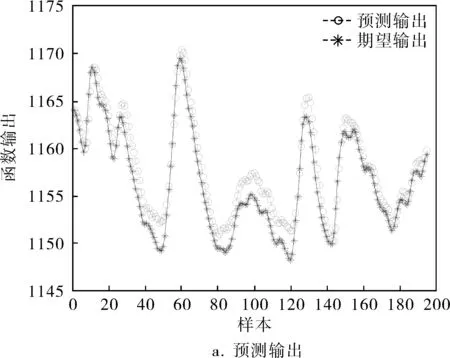
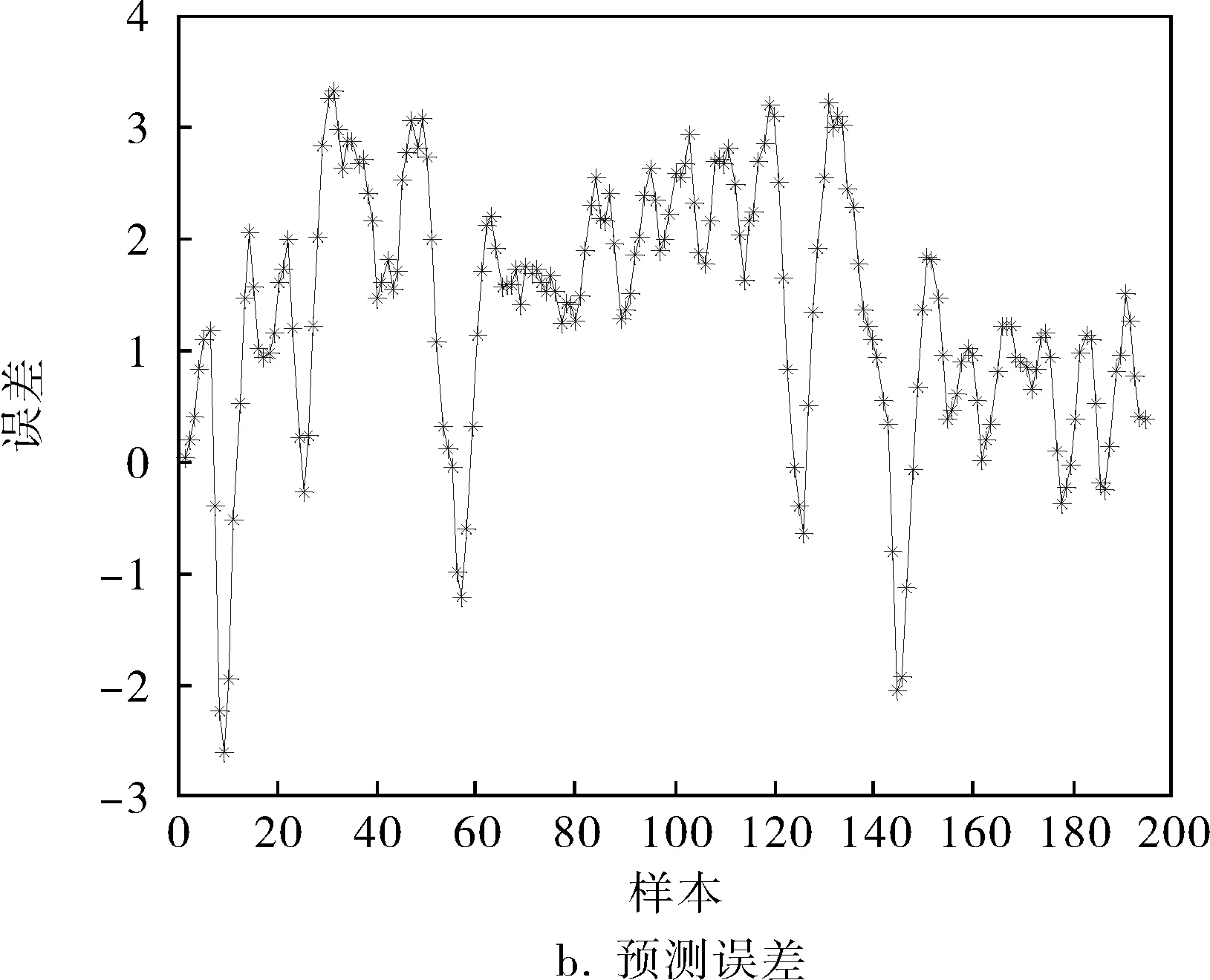
图7 单隐层BP神经网络的预测输出与预测误差

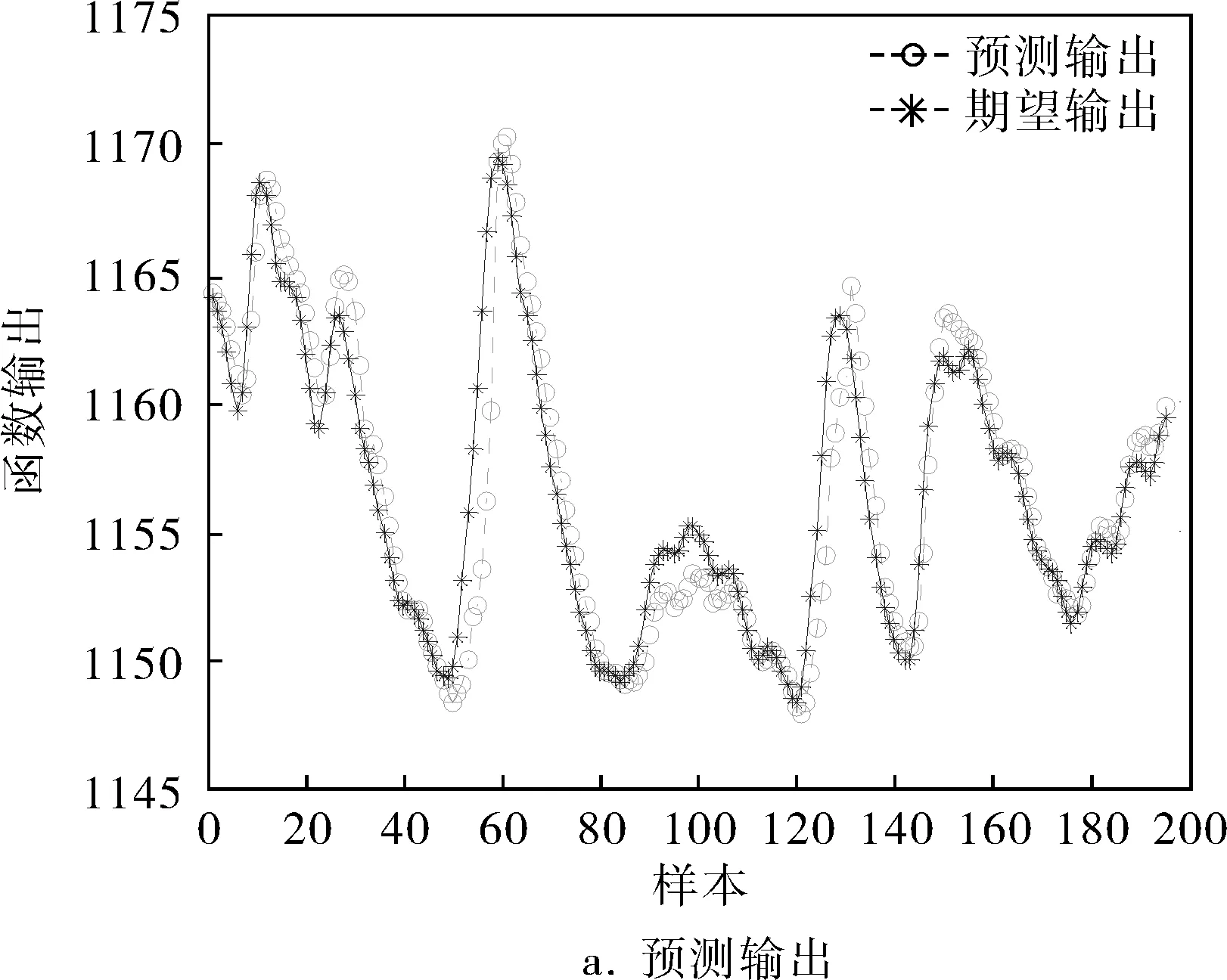
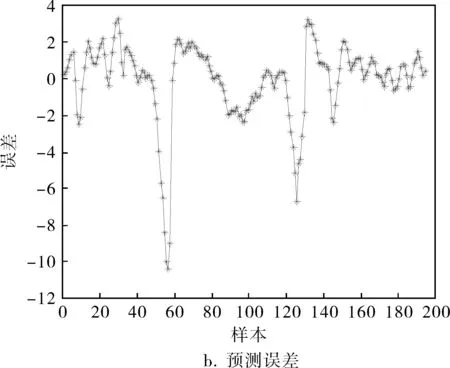
图8 双隐层BP神经网络的预测输出与预测误差

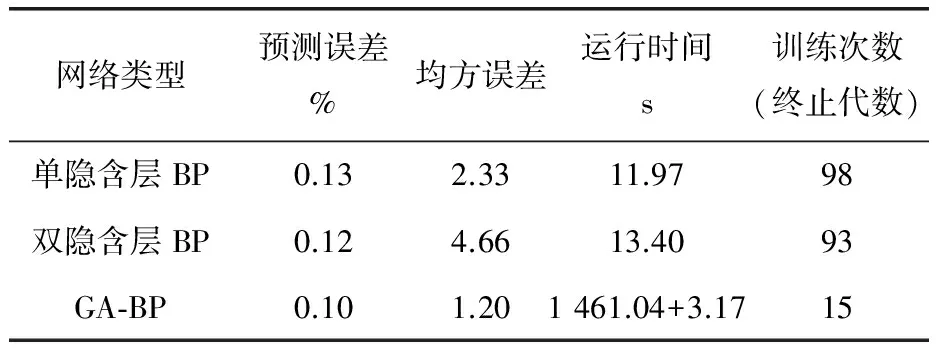
表2 不同BP神经网络的预测结果比较

4 结束语

加热炉建模的准确性对控制效果影响巨大。笔者采用GA-BP算法对加热炉进行建模：综合了GA的全局收敛性和BP算法局部搜索的快速性，使网络学习更加有效；利用GA反复优化神经网络的权值，直到相邻两次优化后适应度值不能继续有效下降为止，再用BP算法对它进行微调，就可以迅速收敛到全局最佳参数组合。仿真结果表明：该方法的通用性较强、稳定性好，在实际应用中有独特优势。但BP神经网络参数的不断增多会导致GA的运算量迅速膨胀，运算时间迅速增加，因此在提高计算速度的同时优化算法并减少计算量，是下一步需要解决的问题。

[1] 王乐一,赵文虓.系统辨识:新的模式、挑战及机遇[J].自动化学报,2013,39(7):933～942.

[2] 唐桂华,庄正宁.炼油厂加热炉节能方案分析[J].化工机械,2000,27(6):352～355.

[3] 刘硕,齐咏生,王林,等.电站锅炉煤耗与NOx排放混合建模与优化[J].石油化工自动化,2016,52(1):30～34.

[4] 荣莉,柴天佑,钱晓龙.加热炉过程控制技术的新策略——智能控制[J].控制与决策,2000,15(3):269～273.

[5] 薛美盛,孙胜杰,袁鑫,等.一种基于历史数据的加热炉温度模糊控制规则提取方法[J].化工自动化及仪表,2016,43(9):940～944.

[6] 蔡自兴,徐光祐.人工智能及其应用[M].北京:清华大学出版社,2010:146～183.

[7] Fausett L V,Hall P. Fundamentals of Neural Networks:Architectures,Algorithms,and Applications[M].NJ:Prentice-Hall Englewood Cliffs,1994:289～334.

[8] 李敏强.遗传算法的基本理论与应用[M].北京:科学出版社,2002.

[9] Wang L,Tang D B.An Improved Adaptive Genetic Algorithm Based on Hormone Modulation Mechanism for Job-Shop Scheduling Problem[J].Expert Systems with Applications,2011,(7):243～250.

[10] 陈晓波,俞迪龙,秦树凯.基于遗传算法的加热炉炉内钢温软测量模型[J].仪器仪表学报,2007,28(2):308～312.

ApplicationofGA-BPNeuralNetworkinReheatingFurnaceModeling

XUE Mei-sheng, YANG Meng, LIU Bo, MENG Jun

(CollegeofElectronicsScienceandTechnology,UniversityofScienceandTechnologyofChina)

In this paper, basing on a large amount of data collected, the BP neural network was used to build a nonlinear model of the temperature of reheating furnace, including making use of genetic algorithm to optimize both parameters and thresholds of the BP neural network to effectively avoid the problem that BP neural network easily falls into local minimum or slow convergence speed. The simulation results show that, the GA-BP neural network is with more stability and higher prediction precision under the same data set.

GA-BP neural network, heating furnace, nonlinear modeling, optimization

薛美盛(1969-)，副教授，从事工业过程先进控制与优化、计算机控制工程、测控网络与技术、环境工程等的研究与开发工作。

联系人杨猛(1991-)，硕士研究生，从事工业自动控制的研究，ymeng@mail.ustc.edu.cn。

TH865；TP391

A

1000-3932(2017)10-0911-06

2017-02-24，

2017-08-06)