基于LabVIEW的相机标定技术研究*

王 皓 杜向阳 耿英博 张克平

(上海工程技术大学机械工程学院)

基于LabVIEW的相机标定技术研究*

王 皓 杜向阳 耿英博 张克平

(上海工程技术大学机械工程学院)

使用LabVIEW平台和视觉开发模块完成对相机的标定，选用圆点阵标定板，利用Canny算子提取圆形轮廓，然后基于亚像素边缘提取的圆拟合方法提取特征点在图像坐标系下点中心坐标。该方法降低了摄像机标定的难度，极大地缩短了软件开发周期，具有较高的标定精度，能够满足实际工业检测的精度要求。

相机标定 机器视觉 LabVIEW Canny算子

机器视觉就是利用计算机和视觉传感器件替代人眼来做度量和判决[1]。近年来，机器视觉技术以非接触、快速、高精度及自动化程度高等优点在各个领域都得到广泛应用。

相机标定是机器视觉检测和定位系统研究中的重要组成部分。相机标定的实质就是求解相机内外参数的过程。目前，用于相机标定的方法多种多样，大致可以分为3类：传统的相机标定方法、主动视觉中的标定方法和相机自标定方法。笔者在基于张正友标定算法的基础上，利用LabVIEW作为开发平台，并考虑到二次径向畸变，建立非线性相机模型，完成对相机的标定。

1 LabVIEW平台与视觉开发模块

LabVIEW作为一种编程语言，与其他常见的编程语言相比，最大的特点在于它是一种图形化编程语言，使程序开发更直观、简洁，界面也更加具有说服力，极大地提高了编程的效率，缩短了软件的开发时间。

视觉开发模块是专为开发机器视觉而设计的，NI视觉开发模块包括IMAQ Vision和NI Vision Assistant，IMAQ Vision拥有强大视觉处理函数的库，NI Vision Assistant提供不通过编程就实现将LabVIEW 应用于快速成型的直观环境。其中IMAQ Vision 是一套包含各种图像处理函数的功能库，它将400 多种函数集成到LabVIEW、Measurement Studio、LabWindows/CVI、Visual C++和Visual Basic开发环境中，为图像处理提供了完整的开发功能；NI Vision Assistant是图像模型建立与验证的一个工具，它能够自动生成LabVIEW程序框图，该程序框图中包含NI Vision Assistant建模时一系列操作的相同功能，而且开发者可以根据实际需求进行二次编写，并将程序框图集成到自动化或生产测试应用中，用于运动控制、仪器控制及数据采集等。

2 相机模型的建立

针孔相机模型是各种相机模型中最简单、常见的一种，这是一种不考虑相机畸变因素而建立的理想状态模型。它的优点是成像关系是线性的，简单实用而且保证准确性，因此在机器视觉中得到了广泛的应用。但是在实际的工程应用中，由于相机镜头的制造和安装中存在一定的误差，镜头均会产生一定的畸变，为了提高相机标定的精度，笔者在理想的针孔相机模型的基础上考虑镜头的径向畸变，从而重新建立相机的成像模型。

2.1针孔相机模型

CCD相机采集获取的图片在计算机内是以M行N列的数组形式保存的，M行N列的图像中的元素称为像素。在图像上定义直角坐标系每一像素的坐标(u,v)分别为该像素在数组中的列数和行数，所以(u,v)是以像素为单位的图像坐标系的坐标。而在实际的工程应用中，需要将以像素为单位的图像坐标系转变成以物理单位毫米(mm)表示的图像坐标系，以物理单位毫米表示的图像坐标系的x轴和y轴分别平行于u轴和v轴，这两个坐标系之间的关系如图1所示。

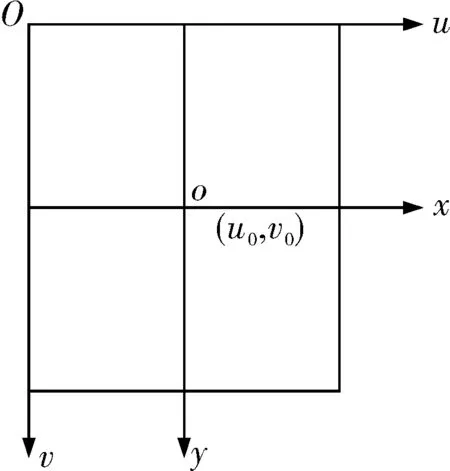
图1 图像坐标系关系

其中o点在(u,v)坐标系中的坐标为(u0,v0)，即图像中每一个像素在x轴和y轴方向上的物理尺寸为dx,dy，所以在图像中，每个像素在坐标系(u,v)和坐标系(x,y)下的关系用齐次坐标与矩阵形式表示为：

(1)

图2为针孔相机模型示意图。针孔相机模型是指在理想状态下，采集的图像点经过透镜成像后，在成像平面上可形成与之对应的理想的像点，使得空间图像点、镜头的光心点和成像点都在一条直线上[2]。设Oc-XcYcZc为相机坐标系、Ow-XwYwZw为世界坐标系，相机坐标系的原点Oc为CCD相机镜头的光心，Zc轴与相机的光轴重合，原点o为相机光轴和图像平面的交点，f为相机的有效焦距，图像平面和XcOcYc平面平行，以物理单位毫米表示的图像坐标系的x轴和y轴分别平行于相机坐标系的Xc轴和Yc轴。(Xw,Yw,Zw)、(Xc,Yc,Zc)分别为空间中任意一点P的世界坐标和相机坐标，(x,y)为点P在图像平面上的投影坐标。

对于空间上任意一点P，在世界坐标系下的坐标(Xw,Yw,Zw)和在相机坐标系下的坐标(Xc,Yc,Zc)之间的变换关系为：

(2)

图2 针孔相机模型示意图

其中，R和T分别表示从世界坐标系到相机坐标系的旋转矩阵和平移矩阵，旋转矩阵R是3×3的正交矩阵，平移矩阵T是3×1的列向量；H1是4×4的矩阵，用于反映相机坐标系和世界坐标系之间的位置关系，表示相机的外参数矩阵。

按图2建立针孔相机模型，得到空间上一点P在图像平面上的坐标用齐次坐标与矩阵形式表示为：

(3)

根据式(1)、(3)得到图像坐标系与相机坐标系之间的转换关系：

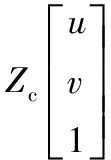
(4)

其中，H2是3×4的矩阵，表示相机的内部参数矩阵；fx、fy、u0、v0只与相机的内部结构有关。根据式(4)，当采集3幅及以上的标定板图像，就可以求出相机内参数矩阵H2。

根据式(2)、(4)得到图像坐标系与世界坐标系之间的转换关系：

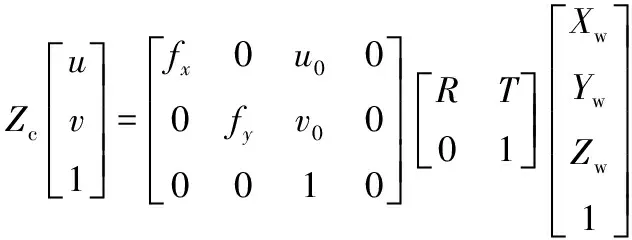
(5)

其中，H是3×4的单应性矩阵。根据式(5)，当已知足够多的空间点的世界坐标及其对应的图像坐标，就可求出H矩阵。知道了投影矩阵H和相机内参数矩阵H2，便可求出相机的外参数矩阵，得到相机的外部参数。确定了相机的内外参数，即完成了相机线性模型的标定。

2.2非线性相机模型

在实际的成像过程中，考虑到相机镜头的制造和安装过程中存在一定的误差，会造成镜头的失真，一般都存在非线性畸变，相机的镜头畸变主要分为3类：径向畸变、偏心畸变和薄棱镜畸变[3]，考虑到非线性畸变，所以在相机标定时使用非线性优化算法。而有研究表明，引入过多的非线性(如偏心畸变和薄棱镜畸变)不仅不能提高解的精度，还会引起解的不稳定，所以笔者在考虑畸变的情况下建立实际的非线性相机模型，而在一般情况下径向畸变就足以描述非线性畸变，因此笔者只考虑径向畸变[4]，建立相机非线性模型的方程如下：

(6)

3 相机标定步骤

笔者利用LabVIEW+NI Vision去完成相机的标定，考虑到圆心提取算法的稳定性和定位精度要优于棋盘标定板的角点提取，因此选用6×8圆点阵列标定板，如图3所示。

图3 圆点阵列标定板

具体的标定步骤如下：

a. 首先选择相机的标定类型为Camera Model(Grid)，用至少5幅标定图像才能得到相机参数和镜头的畸变；

b. 加载采集的标定板图像，为了提高标定的精度，笔者载入11张在不同角度下采集的标定板图像，并按照要求，选用基本上与镜头光轴相垂直的图像1为标定的参考工作平面，并将以此平面为基准来修正镜头的非线性畸变；

c. 对每一幅图像进行阈值参数的选择，将标定板图像上的圆点从背景中清晰地显现出来，若标定版图像上的圆点没有被完全覆盖，则需要手动画出相对应的范围，以保证圆点区域完全显示，并采用Canny滤波器提取圆形轮廓；

d. 输入标定版图像上圆点间的相关参数，包括X Spacing、Y Spacing和Unit，分别表示标定板上相邻圆点之间的X方向上的圆心距离、Y方向上的圆心距离和距离的单位，笔者使用的实际相邻圆点间X方向上和Y方向上的距离均为12，单位为mm；

e. 利用圆拟合算法提取圆心特征点的坐标，得出相机的内参和相应的误差参数，如图4所示；

f. 为标定图像设定坐标系，选取右上角的圆心为坐标圆点，以便在后续测量中得出点的精确坐标值；

g. 最后将标定结果保存为png文件格式，方便在后续的测量中调用。

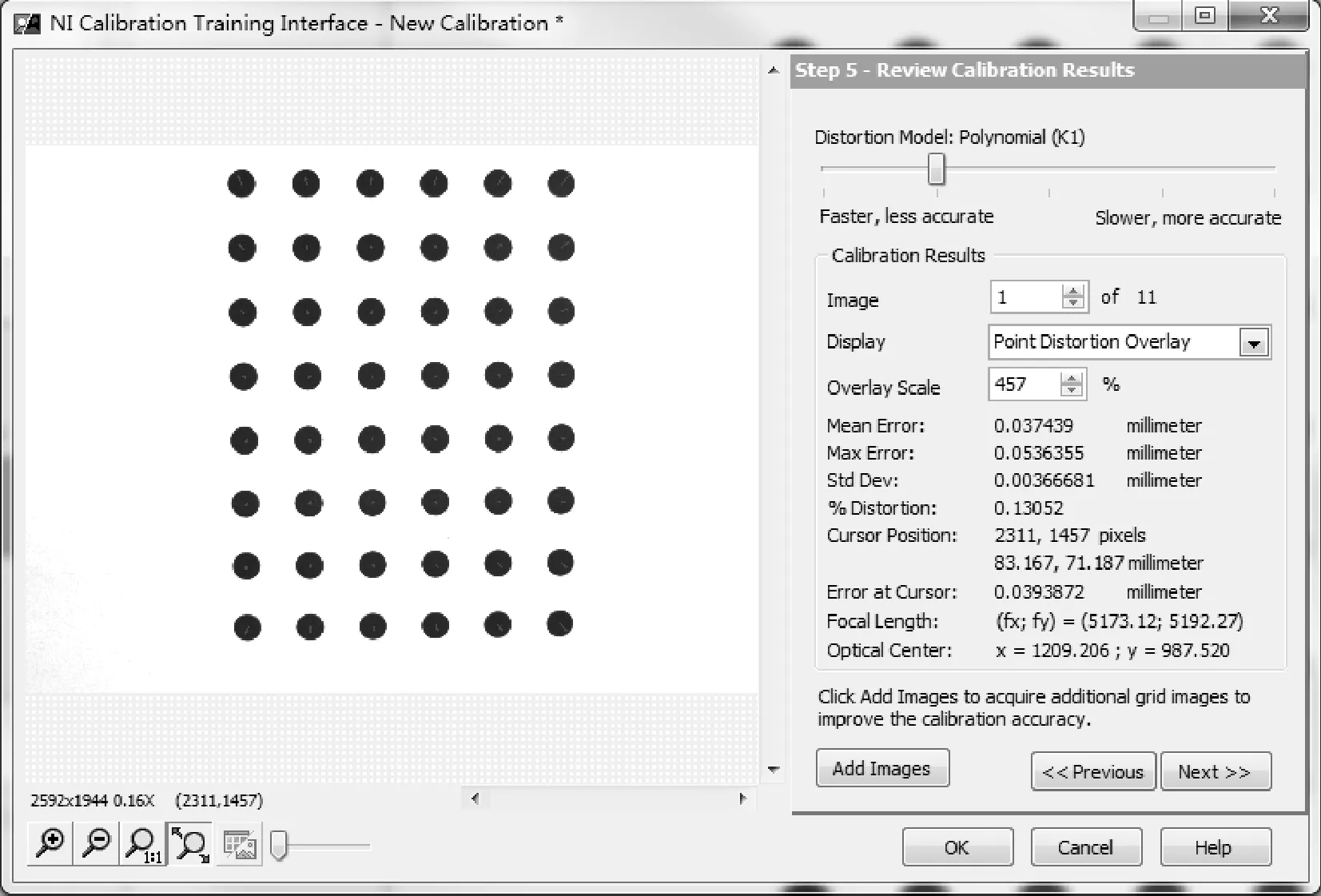
图4 相机标定步骤e

4 实验结果分析

对矫正后的图像进行形状边缘检测，得到圆点阵列标定板中所有圆的半径、圆心的图像坐标及世界坐标等详细的参数，笔者只选取标定板圆点的半径参数数据信息(表1)。

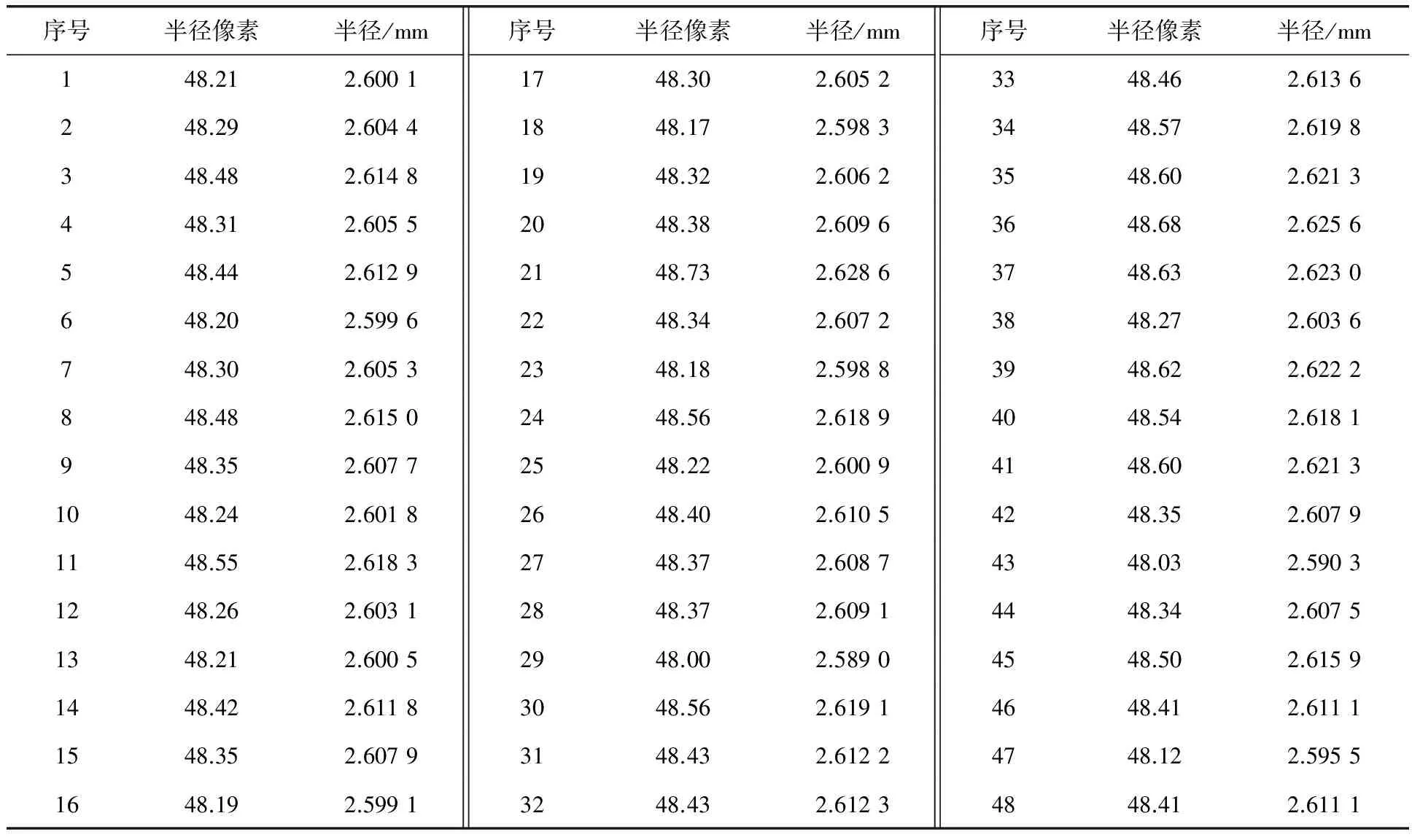
表1 标定板圆点半径参数

实验结果表明该方法矫正效果较好，平均物理误差在0.032 9mm左右，畸变为0.100 7%。

在计量学中，常用标准差衡量所测数据的精度，笔者选用标准差σ对垂直方向相机标定精度进行评定，公式如下：

(7)

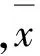
根据表1选取图像圆点的半径结果数据进行具体的分析处理，分别计算得出以像素为单位的圆的半径标准差σpixel=0.1639和以毫米为单位的圆的半径的标准差σmm=0.0088。因此经过上述的数据分析表明，笔者使用的标定方法具有较高的标定精度，能够满足实际机床加工或工业检测的精度要求。

5 结束语

基于LabVIEW 的标定方法可以很有效地消除图像中线性与非线性的畸变，操作简单，标定精度较高，而且能够方便地与NI视觉开发模块结合使用，是传统方法无法相比的，对实际生产有很重大的意义，将会广泛地应用到机械工件加工、零件检测等众多领域，进一步提高自动化程度，极大地提高生产效率，降低成本。

[1] Carsten S, Markus U, Christian W. Machine Vision Algorithms and Applications[M]. Berlin: Wiley-VCH, 2007.

[2] Yang X F, Huang Y M, Gao F.A Simple Camera Calibration Method Based on Sub-pixel Corner Extraction of the Chessboard Image[C].Proceedings of IEEE International Conference on Intelligent Computing and Intelligent Systems.Piscataway,NJ,2010:688～692.

[3] 刘超.移动视觉检测系统的建模与标定方法研究[D].天津：天津大学,2013.

[4] Zhang Z Y. A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,22(11):1330～1334.

TheResearchofTechnologyforCameraCalibrationBasedonLabVIEW

WANG Hao, DU Xiang-yang, GENG Ying-bo, ZHANG Ke-ping

(CollegeofMechanicalEngineering,ShanghaiUniversityofEngineeringScience)

Employing LabVIEW platform and visual development module to calibrate cameras was implemented, including having dot matrix chosen to calibrate the board and Canny operator adopted to extract the circle edge and then having the method of circle fitting extracted based on subpixel edge to get feature points’ coordinate in the image coordinate system. The proposed method can reduce the difficulty of camera calibration and shorten the software development cycle. The most important is that it has a high calibration accuracy as the actual industrial detection required.

camera calibration, machine vision, LabVIEW, Canny operator

王皓(1993-)，硕士研究生，从事图像处理的研究，wanghaoxsj@qq.com。

TP301.6

A

1000-3932(2017)10-0944-05

2017-06-21，

2017-06-30)