高斯-赛德尔法求解光伏阵列最大功率点基准值
王 冰,沈王平,胡庆燚,魏红敏
(河海大学能源与电气学院,江苏 南京 211100)
高斯-赛德尔法求解光伏阵列最大功率点基准值
王 冰,沈王平,胡庆燚,魏红敏
(河海大学能源与电气学院,江苏 南京 211100)
为了快速且准确地求解光伏电池模型参数,进而求解局部阴影条件下光伏阵列的最大功率基准点值,采用高斯-赛德尔法,从工程实际出发,根据局部阴影下的光照情况,把光伏阵列模型分解成光照均匀条件下的多个新光伏阵列模型,利用光伏电池数据手册可以快速且准确地求解模型参数。仿真结果表明:高斯-赛德尔法能够快速且准确地求解拆分后模型的光伏阵列最大功率点基准值;该方法适用于光伏阵列在局部阴影条件下的输出特性和各个峰值点最大功率基准值求解问题。
高斯-赛德尔法;光伏阵列分解;局部阴影;最大功率点;输出特性;峰值点
当光伏电池板安放在城市的屋顶上时,容易受到阴影的影响出现多峰值情况,由于各个峰值点的功率相差较大,若陷入局部最大功率点,会导致很多能量的损失。因此,解决局部阴影情况下光伏电池最大功率点跟踪问题,有助于城市居民自家小型光伏发电系统的应用,对城市光伏发电具有重要意义[1-2]。
求取光伏阵列最大功率点首先要确定光伏电池模型中包含的参数,而光伏电池模型是一个包含5个参数的隐式超越非线性函数方程,求解较复杂。传统模型参数求解方法主要有电导简化法、数值拟合法等[3-4],电导简化法和数值拟合法的计算过程复杂,不便掌握。目前运用最多的五点测量法[5-6]可以有效地求出模型参数,但需获取光伏电池I-U特性曲线的短路点和开路点导数,而光伏电池生产厂家提供的产品数据手册中并不包含这2个数据。为此,本文提出了一种利用产品数据手册来确定模型参数的方法,在仅知道光伏电厂家提供的产品数据的情况下,能够快速而准确地求出标准情况下模型的参数。
高斯-赛德尔法是求解非线性方程有效的方法,通过设置误差精度可以得到精确的解。当光伏阵列处于局部阴影情况下时,根据阵列的阴影分布将光伏阵列分解成多个光照均匀的新光伏阵列,利用高斯-赛德尔法求解所需参数,准确分析光伏阵列在局部阴影情况下的输出特性,以及求得各个峰值点,从而得到最大功率点基准值。
1 光伏特性分析
光伏电池由半导体材料制成,本身是一个PN结,它的输入输出具有强烈的非线性特征。通过对其物理模型[7]分析,将其等效为一个二极管与太阳能电流源以及一系列电阻(串联和并联电阻)组成的等效电路,光生电流在负载两端建立起端电压。等效电路[8-11]的光伏电池I-U方程为
(1)
式中:U、I——光伏电池模型的电压、电流;Iph、I0——光生电流、二极管的反向饱和电流;Ut——二极管的结热电压;Rs、Rsh——等效电路的串联电阻、并联电阻;ns——二极管影响因子。
单个光伏电池输出功率太小,无法满足发电的要求,所以通常将多个光伏电池通过串、并联的方式组合成光伏阵列。假设有N个光伏阵列,每个阵列中包含了M个光伏电池,光伏阵列模型为
(2)
式中:Ipv——光伏阵列的电流;Upv——光伏阵列的电压;k——玻尔兹曼常数,k=1.38×10-23J/K;T——PN结热力学温度;q——电子所带电量,q=1.6×10-19C。

图1 光伏阵列在局部阴影条件下的示意图Fig.1 Schematics of PV array under local shading conditions
光伏阵列在光照均匀的情况下是一个单峰值的曲线,形状与单个光伏电池的输出曲线基本一致。但是由于多个光伏电池通过串、并联的方式连接到一起,所以其开路电压和短路电流成倍增大。基于单个光伏电池和光伏阵列之间的关系,下述内容将多个光伏阵列等效为单个光伏电池来求解。
1.2 光照不均匀条件下光伏阵列输出特性
光伏阵列板容易受到树荫、高楼的遮挡,就是在沙漠里的大型光伏电场,也可能受到云层的遮挡。此时光伏阵列就处于局部阴影条件下。当光伏阵列受到的光照强度不均匀时,整个光伏阵列的输出特性就会发生变化。图1是光伏阵列在局部阴影条件下的示意图。
模拟光伏阵列光照强度,3行光伏阵列的取值分别为1 000 W/m2、800 W/m2和600 W/m2。得到的光伏阵列输出特性曲线如图2所示。
从图2可以看出,当光伏阵列在局部阴影条件下时,光伏阵列的P-U曲线是一个多峰值的非线性曲线,I-U曲线是形如多层阶梯形的非线性曲线,产生多个峰值点是因为各个光伏电池所受到的光照强度不同导致了输出功率不同。

图2 光伏阵列在局部阴影条件下输出特性曲线Fig.2 Output characteristic curve of PV array under local shading condition
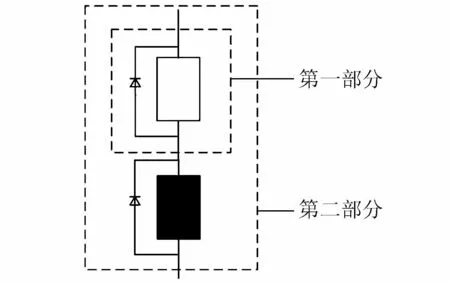
图3 单串等效电路示意图Fig.3 Schematics of equivalent single string
2 光伏电池参数求解
在局部阴影条件下,由于光伏电池受到光照强度和温度不同,导致每个光伏电池的工作状态不同。根据光伏阵列的输出特性,把在局部阴影条件下光伏电池分解为几个光伏阵列[12]。当有2个光伏电池串联成为一个单串时,根据光伏电池等效电路,可以将此单串等效为两部分,如图3所示。
单串分解为两部分,其数学表达式为
(3)
式中:U1、U2——第一部分和第二部分的电压;U——单串光伏的总电压;ID——流经二极管的电流;Iph1——第一部的光生电流;Iph2——第二部分的光生电流。
对等效结果验证,2个组件的光照强度分别为1 000 W/m2、600 W/m2。第一部分只有一个组件工作,光照强度为1 000 W/m2;第二部分有2个组件工作,光照强度和光照弱的组件保持一致为600 W/m2。从而得到不同光照强度下的光伏特性曲线,如图4所示。
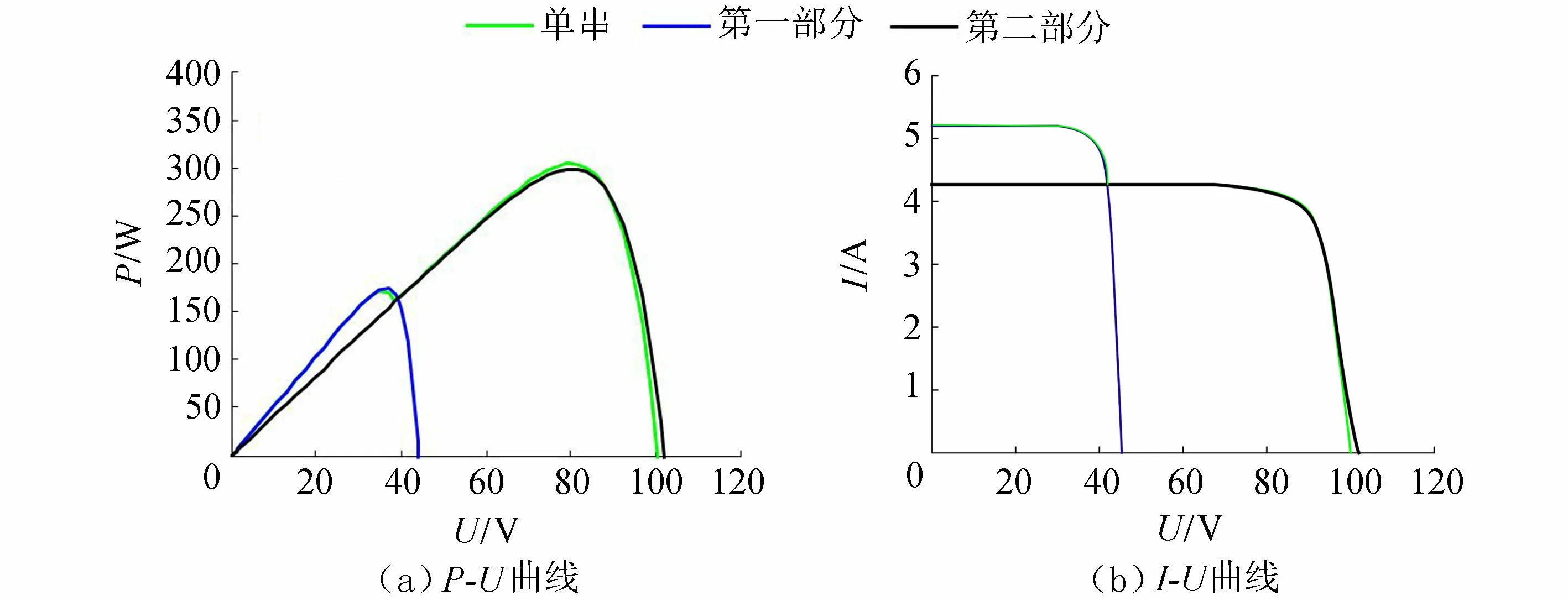
图4 单串等效输出特性曲线Fig.4 Equivalent output characteristic curves of single string
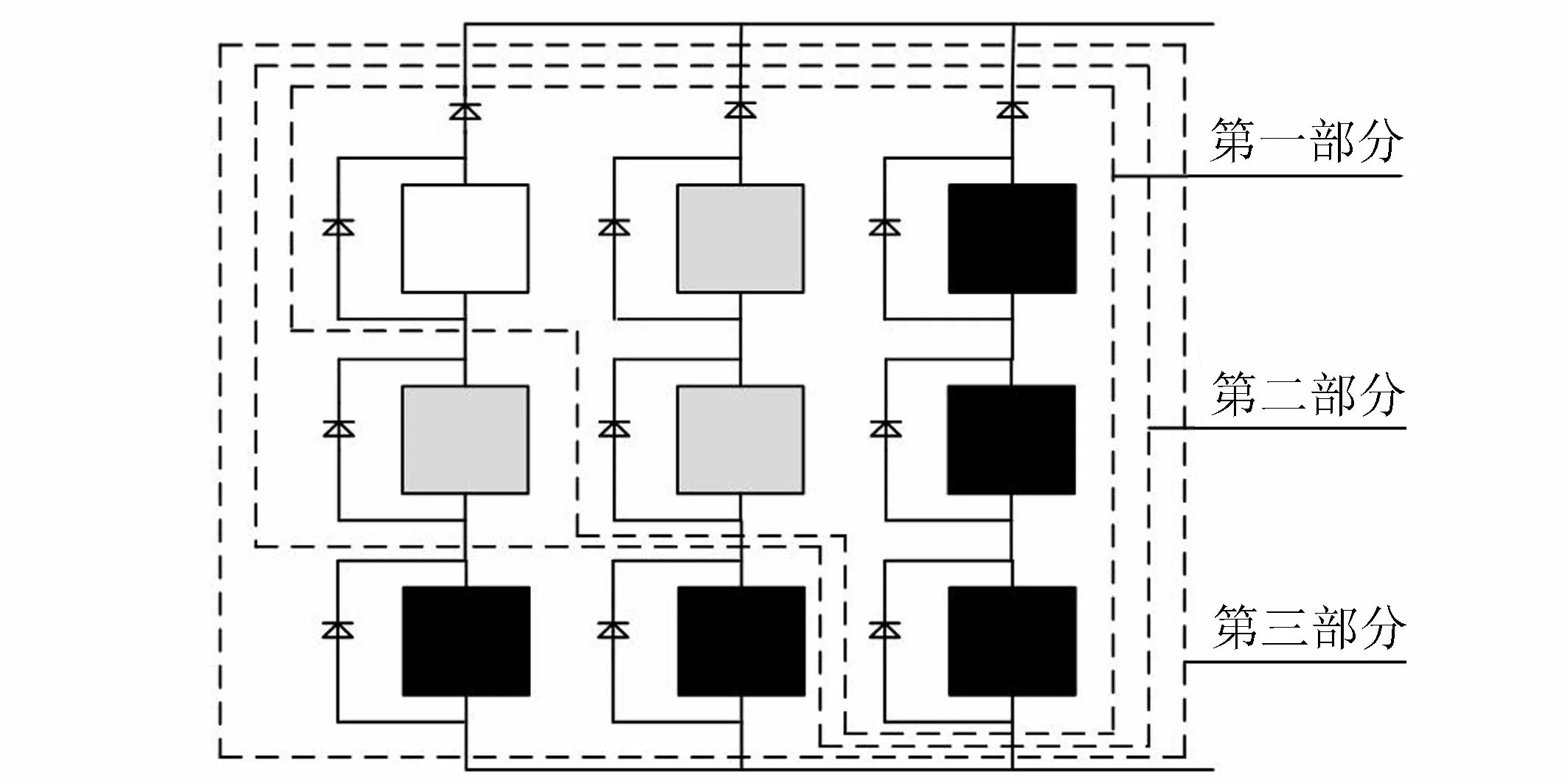
图5 光伏阵列拆分示意图Fig.5 Schematic diagram of PV array splitting
可以看出等效分解把原来含有2个电池的单串分解为两部分,通过仿真可得和单个光伏电池基本一致。通过实验可知,当光伏阵列处于局部阴影条件下时,一个n×n光伏阵列,同样可以对其进行拆分,结果和单个光伏电池基本一致,而且,在同一串光照顺序不会影响阵列的输出特性,即在同一串中,只要阴影部分的光照强度大小不变,单纯改变阴影的位置,对该串输出特性是没有任何影响的。这里以3×3光伏阵列为例,在局部阴影条件下,复杂的光伏阵列受到3种强度的光照,3种光照强度照射的组件个数分别为1、3、5。
应用上述光伏单串分解的方法对第一单串进行分解,再对整个光伏阵列应用基尔霍夫电流定律,可将光伏阵列分解为3个部分,如图5所示。
通过Matlab仿真平台,对拆分后获得的新光伏阵列和原光伏阵列进行输出特性比较,结果如图6所示。
由图6可知,本文提出的光伏阵列分解方法具有一般性。
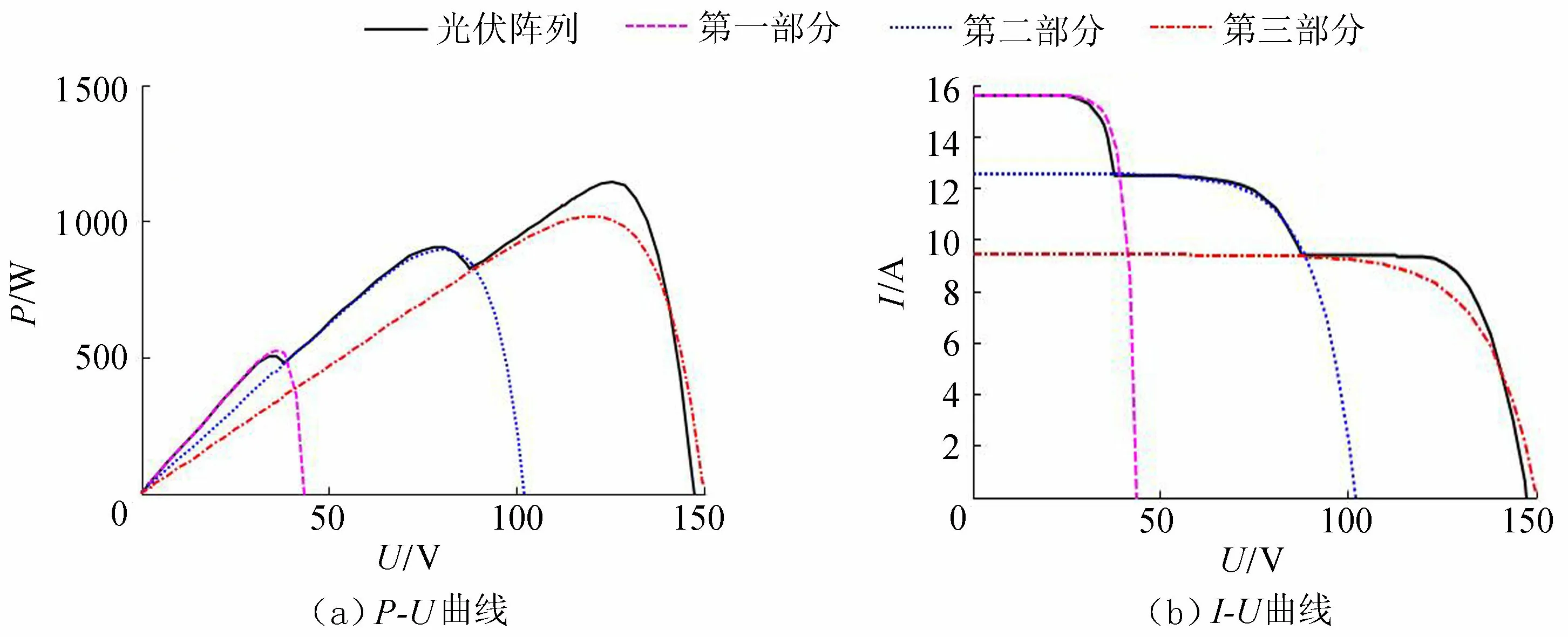
图6 光伏阵列等效特性曲线Fig.6 Equivalent P-U and I-U characteristic curves of PU array
3 最大功率基准值求解
3.1 高斯-赛德尔法

3.2 局部阴影情况下最大功率求解
3.2.1 参数辨识
光伏电池模型参数决定了光伏电池的输出特性。式(1)所表示的光伏电池等效模型存在的未知参数有:Iph、I0、ns、Rs和Rsh。实际工程应用过程中,光伏电池的生产商一般不会提供这些参数值,往往只给出光伏电池的开路电压Uoc、短路电流Isc、最大功率点工作电压Um和最大功率点工作点电流Im。在I-U特性曲线中,(0,Isc)、(Uoc,0)与(Um,Im)被认为是重要标记点。因此,可以利用这几点的数据来求取相关参数。文献[8]提出了一种参数求解的新方法,通过仿真实验,能够较方便地得到光伏电池的4个重要参数I0、ns、Rs和Rsh。
根据重要标记点信息,可以得到:
(4)
(5)
(6)
根据文献[9],可分别求得5个可求取未知参数Iph、I0、ns、Rs和Rsh的方程式。其中,求取ns、Rs和Rsh的式子为超越方程组,同时这3个变量相对于Iph和I0完全独立,这也就使得5个变量的求解转换为ns、Rs和Rsh的求解问题。
通过高斯-赛德尔迭代法,可以分别求得ns、Rs和Rsh的值。
容易看出,在求取参数的过程中,ns的求解是显式方程,而Rs和Rsh的求解为隐式方程。在ns求解中,ns为未知量Rs和Rsh的函数。所以在初始化未知量时,先给Rs和Rsh赋初值,进而得到ns值,然后迭代求得Rs和Rsh的值。通过高斯-赛德尔法可以快速求解出最大功率基准点的几个参数值。
高斯-赛德尔法的初始化只需初始化Rs和Rsh的值,在迭代过程中,为了让Rs和Rsh的初始值选取不会出现发散情况,在选取初始值的过程中一般带有试探性。在绝大多数情况下,初始化后高斯-赛德尔法的计算都会收敛,但是也会在少数情况下收敛失败。此时,通常随机使得Rsh初始值远大于Rs的值。
3.2.2 不同环境下的参数修正
光伏电池在实际应用中往往是处于不同光照强度和温度情况。利用高斯-赛德尔法可以将求解不同光照强度和温度下光伏阵列的最大功率值等效为求解单个电池的最大功率值。当电池处于不同光照强度和温度情况下时,在求出标准状况下模型参数的基础上,对模型参数进行修正。光伏电池模型参数修正公式[13-15]为
(7)
式中:Sref、Tref——标准状况下的入射光强和工作温度;Iph,ref——标准状况下的光生电流;I0,ref——标准状况下的二极管反向饱和电流;Rs,ref——标准状况下的等效电路串联电阻;Eg——材料的能带宽度,它也表现出温度依赖性;β——系数,从文献[16-18]中获知,β≈0.127;Eg,ref——硅电池的能带宽度,在Tref=25℃时的典型值是Eg,ref=1.121 eV。实验观察到二极管影响因子ns随温度和光照强度的变化很小,故ns的变化可忽略。
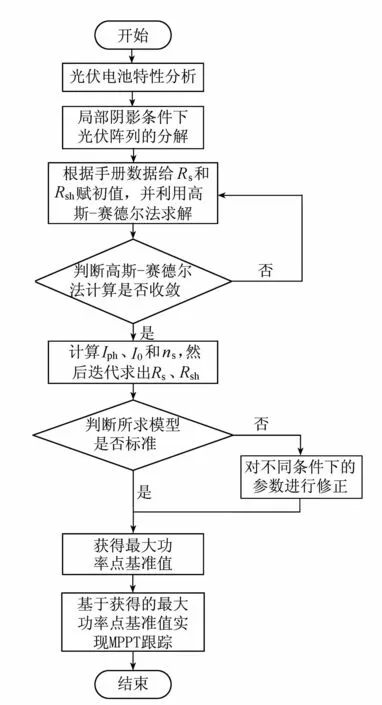
图7 最大功率求解流程Fig.7 Flow chart of the maximum power solving
3.2.3 基于模型的最大功率点求解
基于获得的模型及参数来求解最大功率点基准值。
由文献[19-20]可得到:
(8)
一般光生电流Iph远大于反向饱和电流I0,可认为Iph+I0近似等于Iph。因此可以得到简化的功率求解式子为
(9)

由式(10)求出Im,再代入式(9),可解出Pm。因此,局部阴影下最大功率点基准值求解可以转化成求解任意光照强度和温度下最大功率点,求解流程如图7所示。
4 实 例 验 证
通过MATLAB仿真来验证本文所提方法的准确性和实用性。在标准条件下,某商业用途的光伏电池组件生产商提供的参数为:Isc=4.243 A、Uoc=39.747 V、Im=3.90 8 A、Um=32.311 V。将光伏阵列分解成3个部分,如图5所示。利用高斯-赛德尔法得到标准情况下的求解值如表1所示。

表1 标准情况下的参数设定值、求解值
由表1可以看出,通过高斯-赛德尔方法可以求解出光照均匀条件下所需的参数值,而且误差可控制在5%以内。由此可知,可以利用高斯-赛德尔法进一步辨识局部阴影下的模型参数。
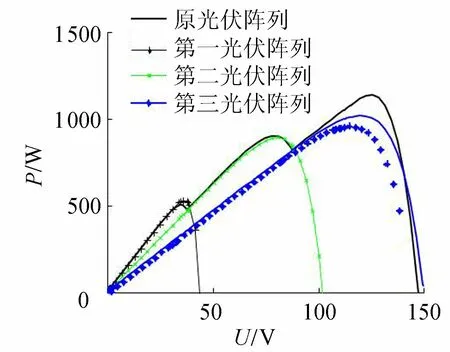
图8 局部阴影光伏阵列与分解后阵列的P-U特性曲线比较Fig.8 Comparison of P-U curves between local shaded PV array and the split array
利用高斯-赛德尔法求解出分解后光伏阵列的各个参数,代入式(9),求解出最大功率点。通过MATLAB进行仿真,得到P-U特性曲线如图8所示。
通过仿真可以验证,对光伏阵列进行分解求取全局的最大功率点是可行的。根据新参数计算出的最大功率点值和原来的最大功率点相比较,可以准确地找到局部阴影情况下光伏阵列的全局最大功率点。
5 结 语
根据光伏阵列的输出特性,将局部阴影条件下光伏阵列模型分解为几个光照均匀情况下的模型。通过利用高斯-赛德尔法快速地求解出最大功率点。本文的研究方法可以推算出任意光照条件下光伏电站的发电量,有助于大规模光伏发电系统的调度,减少由于局部阴影产生的功率损失。
[ 1 ] 王冰清.光伏发电系统MPPT技术研究[D].北京:北京交通大学,2014.
[ 2 ] 戚军,张晓峰,张有兵,等.考虑阴影影响的光伏阵列仿真算法研究[J].中国电机学报,2012,32(32):131-138.(QI Jun,ZHANG Xiaofeng,ZHANG Youbing,et al.Study on simulation algorithm of PV array considering shade effect[J]. Chinese Society for Electrical Engineering,2012,32(32):131-138.(in Chinese))
[ 3 ] 肖景良,徐政,林崇,等.局部阴影条件下光伏阵列的优化设计[J].中国电机工程学报,2009,29(11):119-124.(XIAO Jingliang,XU Zheng,LIN Chong,et al.Optimal design of photovoltaic array under local shadow condition[J].Chinese Journal of Electrical Engineering,2009,29(11):119-124.(in Chinese))
[ 4 ] JONE W R,HUANG W W.Grid-connected photovoltaic genneration system[J].IEEE Transactions on Circuits and Systems,2008,55(3):953-964.
[ 5 ] 周雪松,宋代春,马幼捷,等.光伏发电系统的并网重复控制及仿真[J].电力电子技术,2010,44(5):8-10.(ZHOU Xuesong,SONG Daichun,MA Youjie,et al.Grid-connected repetitive control and simulation of photovoltaic power generation system[J].Power Electronics,2010,44(5):8-10.(in Chinese))
[ 6 ] 吕昌睿,李国杰.局部阴影最大功率点MPPT算法研究[J].电力科学与工程,2012,28(5):12-15.(LYU Changrui,LI Guojie.Theresearch of MPPT algorithm about the maximum power point under partial shading c4onditions[J]. Electric Power Science and Engineering,2012,28(5):12-15.(in Chinese))
[ 7 ] 陈树勇,鲍海,吴春洋,等.分布式光伏发电并网功率直接控制方法[J].中国电机工程学报,2011,31(10):6-11.(CHEN Shuyong,BAO Hai,WU Chunyang,et al.Directgrid-tie power control method for distributed photovoltaic generation[J]. Chinese Journal of Electrical Engineering,2011,31(10):6-11.(in Chinese))
[ 8 ] 高金辉,唐静,贾利锋.太阳能电池参数求解新算法[J].电力系统保护与控制,2012,40(9):133-136.(GAO Jinhui,TANG Jing,JIA Lifeng.Anovelparameter extraction method for solar cells[J]. Power System Protection and Control System,2012,40(9):133-136.(in Chinese))
[ 9 ] 胡庆燚,王冰,张鹏飞,等.基于高斯-赛德尔迭代法的光伏电池参数辨识与最大功率点基准曲线的研究[J].可再生能源,2015,33(12):1803-1808.(HU Qingyi,WANG Bing,ZHANG Pengfei,et al.Research on parameter solution algorithm and reference curve at maximum power point of photovoltaic cell based on Gauss-Seidel iteration[J].Renewable Energy Resources,2015,33(12):1803-1808. (in Chinese))
[10] 廖志凌,阮新波.硅太阳能电池串联电阻的一种估算新方法[J].电工技术学报,2007,23(5):88-92.(LIAO Zhiling,RUAN Xinbo.Anewmethod on computing series resistance of silicon solar cells[J]. Electrical Technology,2007,23(5):88-92.(in Chinese))
[11] 翟载腾,程晓舫,杨臧健,等.太阳电池一般电流模型参数的解析解[J].太阳能学报,2009,30(8):1078-1082.(ZHAI Zaiteng,CHENG Xiaofang,YANG Zangjian,et al.Analyticsolutions of solar cell model parameters.[J]. Acta Energiae Solaris Sinica,2009,30(8):1078-1082.(in Chinese))
[12] 肖文波,刘萌萌,何兴道,等.提取太阳电池参数的解析法和显函数方法的研究[J].光电子激光,2012,23(9):1681-1685.(XIAO Wenbo,LIU Mengmeng,HE Xingdao,et al.Research on analytic and explicit function methods in extracting solar cell parameters[J]. Optoelectronics Laser,2012,23(9):1681-1685.(in Chinese))
[13] 周德佳,赵争鸣,吴理博,等.基于仿真模型的太阳能光伏电池阵列特性的分析[J].清华大学学报(自然科学版),2007,47(7):1190-1112.(ZHOU Dejia,ZHAO Zhengming,WU Libo,et al.Analysis characteristics of photovoltaic arrays using simulation[J]. Tsinghua University (Natural Science),2007,47(7):1190-1112.(in Chinese))
[14] SERA D,KEREKES T,TEODORESCU R, et al. Improved MPPT method for rapidly changing environmental conditions[J]. IEEE International Symposium on Industrial Electronics, 2006, 1:1420-1425.
[15] 黄存荣,王冰,程永乐,等.光伏电池参数求解与最大功率点基准值的研究[J].可再生能源,2012,30(6):26-29.(HUANG Chunrong,WANG Bing,CHENG Yongle,et al.Research on parameter solution algorithm and reference value at maximum power point of photovoltaic cell[J]. Renewable Energy Resources,2012,30(6):26-29.(in Chinese))
[16] 周建良,王冰,张一鸣.基于实测数据的光伏阵列参数辨识方法与输出功率预测[J].可再生能源,2012,30(7):1-4.(ZHOU Jianliang,WANG Bing,ZHANG Yiming.Parameter identification and output power prediction of photovoltaic array based on the measured data[J]. Renewable Energy Resources,2012,30(7):1-4.(in Chinese))
[17] KASHIFI Z S.A deterministic particle swarm optimization maximum power point tracker for photovoltaic system under partial shading Condition [J].IEEE Transaction on Industial Electronics,2013,60(8):3195-3206.
[18] DIETER K S.Semiconductor material and device characterization,seconded[M].New York:Jhon Wiley amp; Sons Inc,1998.
[19] MESSENGER R A, VENTRE J. Photovoltaic systems engineering, seconded[M]. Boca Raton: CRC Press LLC, 2004.
[20] ABIR C, ALI K, KAPOOR D. Identification of photovoltaic source[J]. IEEE Transactions on Energy Conversion, 2011, 26(3): 883-889.
·简讯·
中英城市洪涝防治研讨会暨2017(第三届)城市防洪排涝国际论坛隆重举行
2017年10月16日,中英城市洪涝防治研讨会暨2017(第三届)城市防洪排涝国际论坛在河海大学国际交流中心隆重举行。中英城市洪涝防治研讨会由中国工程院和英国皇家工程院主办,中国工程院国际合作局、中国工程院土木水利与建筑工程学部、南京水利科学研究院和河海大学等单位共同承办。由中国工程院土木水利建筑学部、中国土木工程学会、中国水利学会共同主办的第三届城市防洪排涝国际论坛同时召开。中国工程院副院长樊代明院士和英国皇家工程院院士、中国工程院外籍院士Ian Clukie 先生分别代表主办单位致辞。国家防汛抗旱总指挥部办公室督察专员王磊先生讲话。中国工程院院士、英国皇家工程院外籍院士、南京水利科学研究院张建云院长主持开幕式。河海大学党委书记唐洪武、校长徐辉出席开幕式。
中英城市洪涝防治研讨会以“变化环境下的城市防洪排涝”为主题,第三届城市防洪排涝国际论坛以“重塑绿色可持续发展城市水环境”为主题,两个论坛强强联合,共同聚焦城市暴雨洪水、城市洪涝防治和海绵城市建设3个议题,涉及变化环境下的城市暴雨洪涝规律、城市洪涝监测、城市洪涝模拟分析、城市洪涝风险管理、城市低影响开发等方面,共设有13个大会报告和3场专题讨论。大会邀请中国工程院院士丁一汇做了题为《气候变化与城市化效应对中国超大城市极端暴雨的影响》的报告,英国国家气象局城市环境及气象顾问Damian Wilson做了题为《Climate change implications for weather and flooding》的报告,英国皇家工程院院士、中国工程院外籍院士Ian Cluckie做了题为《Urban flood estimation using rain gauge and radarmeasurements》的报告,中国工程院院士王浩做了题为《城市洪涝模拟与管理》的报告,英国生态与水文中心水文气象灾害主管Nick Reynard做了题为《Incorporating urban growth and climate change intoflood estimation and long-term flood prediction》的报告,英国皇家工程院院士Roger Falconer做了题为《Flood Modelling and Hazard Risk for Extreme Eventsin Urban Environments》的报告,北京师范大学教授徐宗学做了题为《北京市城市化对暴雨洪水过程的影响及其数值模拟》的报告,英国皇家工程院院士Dragan Savic做了题为《From Flood Risk Analysis to Early Warning Systemsfor Megacities of the Future》的报告,河海大学教授杨涛做了题为《高密度城市化条件下突发性特大洪涝灾害:形成机制与精细化风险预警模型》的报告,英国特许水务和环境管理学会高级政策顾问Laura Grant做了题为《The state of sustainable drainage systems (SuDS)delivery in the UK》的报告,北京市市政工程设计研究总院总经理张韵做了题为《海绵机场-北京新机场设计》的报告,Cranfied 大学教授,英国环境署原署长Paul Leinster做了题为《Natural Flood Management on the River Aire andRiver Calder Catchments》的报告,中国工程院院士、英国皇家工程院院士、南京水利科学研究院院长张建云做了题为《中国城市防洪和海绵城市建设》的报告。报告内容丰富、精彩纷呈,引起与会代表热烈反响。
(本刊编辑部供稿)
ReferencevaluecalculationatthemaximumpowerpointofthephotovoltaicarrayusingGaussSeidelmethod
WANGBing,SHENWangping,HUQingyi,WEIHongmin
(CollegeofEnergyandElectricalEngineering,HohaiUniversity,Nanjing211100,China)
This paper is aimed to quickly and accurately solve the parameters of photovoltaic (PV) cell model, in which the reference value at the maximum power point of the local shaded PV array is calculated. To address this issue, Gauss Seidel method is used. Based on the local shading conditions in practical engineering, the PV array model is split into a number of new PV array models under uniform light, the latter are supposed to be solved using the data manual of PV cell. The simulation results show that the reference value at the maximum power point of the split PV array model can be solved quickly and accurately by using the Gauss Seidel method. This would demonstrate that the method is suitable to model the output characteristics of PV array under local shading condition and solve its maximum power point value of each peak point.
Gauss Seidel method; photo voltaic array decomposition; local shade; maximum power point; output characteristics; peak point
10.3876/j.issn.1000-1980.2017.06.011
2016-12-09
王冰(1975—),男,江苏扬州人,副教授,博士,主要从事非线性控制、光伏发电以及新能源研究。E-mail: icekingking@hhu.edu.cn
TM615
A
1000-1980(2017)06-0543-07

