三维洪水流动的SPH数值模型
邵家儒,杨 瑜
(重庆理工大学机械工程学院,重庆 400054)
三维洪水流动的SPH数值模型
邵家儒,杨 瑜
(重庆理工大学机械工程学院,重庆 400054)
对光滑粒子动力学(SPH)方法进行了改进,提出了高精度的耦合动力学边界处理方法,保证粒子的无穿透条件,通过液面粒子的支持域求和准确施加自由液面条件,准确预测水流的翻卷、破碎效应。建立洪水流动的简化模型,分析防波堤对洪水的阻碍作用,准确预测洪水流动中各种三维特征。应用SPH模型对三维圆柱形水体坍塌过程进行模拟,结果表明,SPH数值模拟结果与实验结果吻合很好,从而验证了SPH模型模拟剧烈自由液面流动的有效性。
光滑粒子动力学;自由液面;洪水;耦合动力边界
洪水是一种严重的自然灾害,根据其形成原因可以分为暴雨洪水、溃坝洪水、融雪洪水等。洪水发生时,水流会向下游急速传播,具有很强的突发性和危害性,严重影响人们的生命和财产安全[1-2]。洪水流动涉及水体自由表面变化、翻卷、破碎,复杂的紊流与漩涡,以及强烈的液固耦合作用。数值模拟方法花费少、可重复性好,没有实验测试中可能出现的各种风险,并且可以研究流动中的强非线性特征,已经逐渐成为研究自由液面流动及其与结构耦合作用问题的重要方法[3-6]。
传统基于网格的方法,如有限差分方法[7]、有限体积方法,已经广泛用于计算流体力学的研究中,并逐渐发展了一些自由表面追踪技术,如VOF、 Level set等[8-9]。然而在不规则的复杂区域上构造规则的网格是比较困难的,常常需要复杂的数学变换,同时网格发生畸变时也会大大降低该方法的精度。近年来,很多学者将研究方向转移到光滑粒子动力学(smoothed particle hydrodynamics,SPH)方法[10-11]上来,并取得了很多成果。Shao等[12]对二维溃坝问题进行了数值模拟,应用密度修正和核梯度修正消除了流场中的数值震荡,得到了光滑的压力场。Marrone等[13]应用边界虚粒子法对溃坝相关问题进行了研究;杨秀峰等[14]应用修正的SPH方法在水波破碎方面进行了相关研究;Liu等[15]提出了一种改进的耦合动力边界条件,提高了溃坝流固体壁面上的插值精度,比较准确地预测了压力响应。已有的工作大多针对二维模型展开研究,本文针对两种典型的三维溃坝情况进行数值模拟,以准确预测溃坝流动及有无防波堤对溃坝的影响。
1 SPH 方法
1.1 SPH 控制方程
溃坝流动问题主要由N-S方程控制,其具体形式如下:

(1)

(2)
式中:ρ——密度;t——时间;v——速度;P——压强;g——重力加速度;μ——动力黏性系数。为了将该方程应用于数值模拟,需对其进行数值离散。SPH方程的离散过程分为两步,即核近似和粒子近似,离散后的SPH形式的控制方程描述如下:
(3)
(4)
其中vij=vi-vjxij=xi-xj
式中:m——粒子质量;W——光滑函数[16];h——光滑长度;x——粒子位置;r——粒子间的距离;i、j——粒子编号。光滑函数不仅决定函数近似形式、定义粒子支持域的尺寸,而且还决定核近似和粒子近似的紧致性和精度。本文模拟应用了3次样条函数,其对应的支持域半径为2倍光滑长度,具有较好的紧致性。其表达式如下:
(5)
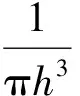
式中:R——粒子间距与光滑长度之比。
1.2 核梯度
(6)
(7)
在每个时间步粒子搜索结束后,只需进行一次核梯度相关矩阵的计算就可以将结果覆盖于所有的场变量,从而提高所有导数的求解精度。
每个诗节充满了跨诗行连续的句子,这也是诗人精心的编排。这种跨诗行连续句的使用,能够产生驱动效果。不完整句子的诗行自然吸引读者去补全缺失,寻找完整的句子和意义,读者在驱动下顺着诗人的指引去找回消逝的童年和童年记忆中的美好生活。另外,跨行的连续句在诗歌中占有一定的比重,有助于营造一幅连续动态伊甸园般的田园景象,如同在读者面前缓缓展开画卷——那里有屋旁的苹果树,幽谷上的星空,成群的马车,田野里的雏菊大麦和闪耀着苹果光辉的小河……这种连续的句子把大自然的美一一展现,带给读者无尽的遐想。
1.3 改进的耦合动力学边界
本文提出一种改进的耦合动力学边界处理方法,如图1所示。固壁边界由两类固定的虚粒子构成,第一类虚粒子称为排斥力粒子,均匀分布在固壁边界位置,它对邻近边界的粒子作用排斥力,阻止粒子的非物理穿透;第二类虚粒子均匀分布在边界外,其层数由所应用核函数的支持域半径来确定,从而保证真实粒子的支持域内不会出现粒子缺失。

图1 改进的耦合动力学边界粒子分布示意图Fig.1 Schematics of particle distributions in the modified coupled dynamic boundary
对于边界粒子的压力和速度,应用如下形式进行计算:
(8)
(9)
该计算形式可以恢复核函数的归一化性质,提高边界粒子相关物理量的计算精度,同时可以保证边界上的无滑移条件。
1.4 自由液面判定
自由液面附近的粒子支持域上会存在一定的粒子缺失,根据该特征可以根据粒子支持域上核函数插值公式建立判定条件,即
(10)
判定为自由液面粒子后则可以设定此类压力为零,其密度为初始参考密度。
2 数 值 算 例
2.1 圆柱形水体坍塌过程数值模拟
为了验证三维SPH模型的有效性,本文首先对圆柱形水体在圆柱形容器中的坍塌过程进行了数值模拟。模型数据来源于Maschek等[17]的试验,如图2所示,Dc=0.11 m,Hc=0.2 m,Dv=0.44 m。模拟过程中初始粒子间距为0.002 5 m,流体密度为1 000 kg/m3,流体使用了约12万个粒子来代替,圆柱形刚体壁面由3层粒子构造,使用了约20万个粒子。
水体坍塌过程如图3所示,初始时刻水体保持静止,在重力的作用下下端水体沿着底部壁面向周围蔓延(如0.1 s时刻),并逐渐铺满整个底面(如0.2 s时刻)。之后底部水体与圆柱形壁面发生撞击,产生较大的冲击,沿着刚体壁面向上运动(如0.3 s时刻),当水体达到一定高度后,动能衰减为零,开始下落回流(如0.4 s时刻),并在容器底部聚集(如0.6 s时刻),此时容器中心处的水体受到挤压,从底部的形心处向上流动,形成喷射状的水柱。通过与Maschek等[17]的试验结果对比,可以看到,SPH模拟结果与试验结果吻合较好,证明改进的SPH方法可以很好地模拟三维自由表面液体流动问题。

图3 SPH结果与试验结果对比Fig.3 Comparison between SPH and experimental results
2.2 洪水流动对建筑的冲击
近年来,由强暴雨导致的溃坝及溃堤事件频发,溃坝及溃堤洪水给人们的生命财产构成了巨大威胁,尤其对位于洪流演进路线上及周边的城镇危害最大。笔者针对水流对城区建筑物的冲击问题建立了简化模型,并进行了数值模拟。
复杂街区模型如图4所示,街区有两排结构相同、建筑高度相同的长方体形构成。街区位于一个长18 m、宽5 m的长方体空间内,建筑物的尺寸均为5.0 m×1.0 m×1.0 m,街区(第一排建筑物)距离水坝的距离为7.5 m,同一排建筑物间相距0.5 m,第一排与第二排建筑物间相距1 m,左侧水体长4.5 m、宽5 m、高2.5 m,初始时刻保持静止。模型粒子间距为0.1 m,其中水体粒子约59 000个,防波堤由3层粒子组成,粒子数约为1 600个,长方体空间的边界为刚体壁面,粒子数约为58 000个。

图4 洪水流动模型示意图Fig.4 Schematics of the flooding flow model
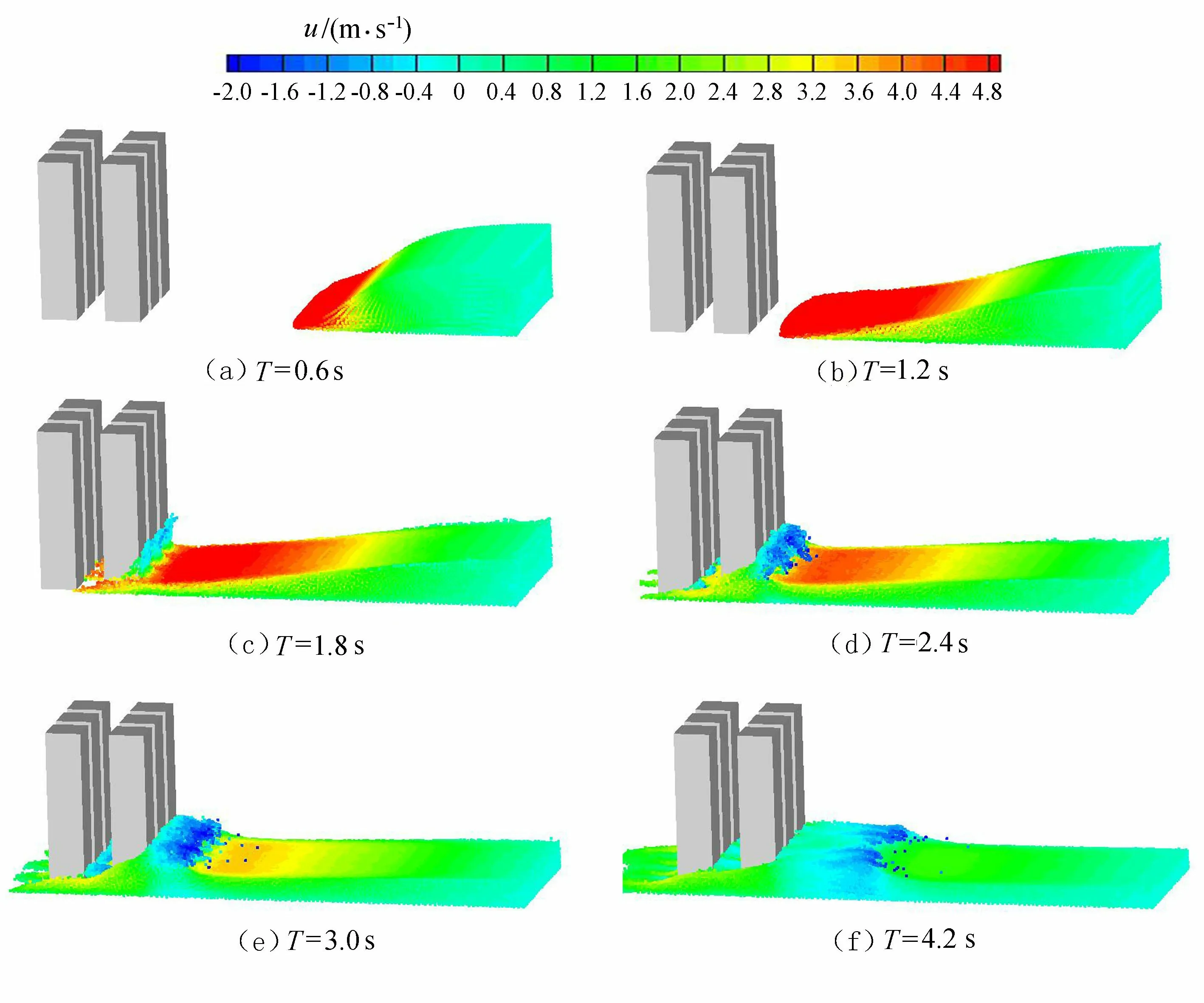
图5 水流冲击过程及速度场变化示意图Fig.5 The impact process and velocity field of the flood flow
从图5可以看到,受到复杂街区影响的洪水水流呈现出复杂的水流特征,如水跃、水波涡旋、水流间断等,这些特性具有很强的三维特性(u为流体的水平速度)。洪水水流在每个建筑的后方都形成了湖区,同时在建筑物的阻碍作用下水波发生破碎,速度方向发生改变,反向流动速度超过2 m/s(如3.0 s时刻)。受复杂街区影响,洪水水流演进到建筑物后方的空地上后形成了很多间断水涡。上述水流特征都是典型的三维流态,可见三维SPH数值模型能比较合理地模拟复杂的水流形态(图6)。

图6 洪水流动俯视图Fig.6 Top view of the flood flow
2.3 防波堤对洪水水流的阻碍作用
为了研究防波堤对水流运动产生的影响,本文在距离左侧8 m(与水体左侧壁面间的距离为3.5 m)处设置一个高1.0 m的防波堤(图4中的黑色区域)。在防波堤作用下,洪水呈现出了更为复杂的水流特征。如图7所示,水流与防波堤撞击之后会沿着防波堤向上运动,此过程中水平流动速度大大降低(如1.2 s时刻)。水体越过防波堤后回落,这一过程中会在防波堤的左侧出现巨大的空腔,相互作用过程中,水波从破碎状态逐渐恢复为较稳定的流动状态,直到与建筑物相遇。

图7 有防波堤时的水流冲击过程及速度场变化示意图Fig.7 The impact process and velocity field of the flood flow with a bulwark
由图5~8可知,防波堤对洪水的运动有巨大的阻碍作用。如T=1.8 s时刻,在无防波堤作用时,洪水已经蔓延到了第一街区,并向第二街区继续运动,而有防波堤阻碍时洪水刚刚越过防波堤。从图8中T=3.0 s及T=4.2 s时的速度分布可以看到,有防波堤作用时水流的流量和流速明显降低,这表明防波堤对洪水起到很大的截流作用,街区中的水位变低,这将大大降低城市排水系统的排水压力。

图8 有防波堤时的洪水流动俯视图Fig.8 Top view of the flood flow with a bulwark
3 结 语
本文建立了洪水流动问题的三维SPH数值模型。基于泰勒级数展开的核梯度计算可以提高函数导数的计算精度,改进的耦合动力边界处理能够保证边界粒子的规则分别及无穿透条件,结合自由液面条件可以准确地预测水流的翻卷、破碎等效应。圆柱体水流坍塌问题中模拟结果与实验结果吻合良好,验证了改进的SPH方法的有效性。有无防波堤作用下的洪水流动模拟表明,SPH模型可以准确预测洪水流动中的各种复杂三维特征,对于工程问题具有一定的指导作用。
[ 1 ] 王立辉,胡四一.溃坝问题研究综述.水利水电科技进展[J].2007,27(1):80-85.(WANG Lihui,HU Siyi.Study on dam failure-related problems[J].Advances in Science and Technology of Water Resources,2007,27(1):80-85.(in Chinese))
[ 2 ] 周克发,李雷.基于社会经济发展的溃坝洪水损失动态预测评价模型[J].长江流域资源与环境,2015(增刊1):147-150.(ZHOU Kefa,LI Lei.Dynamic forecasting evaluation model of flood loss due to dam breach based on socioeconomic development[J].Resources and Environment in the Yangtze Basin,2015(Sup1): 147-150.(in Chinese))
[ 3 ] 王军,梁忠民,施晔.基于GIS的水库洪水风险图编制[J].河海大学学报(自然科学版),2010,38(1):20-25.(WANG JUN,LIANG Zhongmin,SHI Ye.Mapping of flood risk of reservoirs using GIS technology[J].Journal of Hohai University(Natural Sciences),2010,38(1):20-25(in Chinese))
[ 4 ] 邓鹏,李致家.3种水文模型在淮河息县流域洪水模拟中的比较[J].河海大学学报(自然科学版),2013,41(5):377-382.(DENG Peng,LI Zhijia.Comparison of three hydrological models in flood simulation for Xixian Basin of Huaihe River[J].Journal of Hohai University(Natural Sciences),2013,41(5): 377-382.(in Chinese))
[5] 包红军,王莉莉,李致家,等.基于Holtan产流的分布式水文模型[J].河海大学学报(自然科学版),2016,44(4):340-346.( BAO Hongjun,WANG Lili,LI Zhijia,et al.A distributed hydrological model based on Holtan runoff generation theory[J].Journal of Hohai University(Natural Sciences), 2016,44(4):340-346.(in Chinese))
[6] 刘佳嘉,周祖昊,贾仰文,等.分布式水文模型子流域编码方法对比分析[J].河海大学学报(自然科学版),2017,45(1):22-29.(LIU Jiajia,ZHOU,Zuhao,JIA Yangwen,et al.Comparison analysis of subwatershed codificationmethods for distributed hydrological model[J].Journal of Hohai University(Natural Sciences), 2017,45(1):22-29.(in Chinese))
[ 7 ] THOMAS J W.Numerical partial differential equations: finite difference methods[M].New York:Springer Science amp; Business Media,2013.
[ 8 ] RAEINIA Q,BLUNT M J,BIJELJIC B.Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method[J].Journal of Computational Physics,2012,231(17): 5653-5668.
[ 9 ] DOYEUX V,GUYOT Y,CHABANNES.Simulation of two-fluid flows using a finite element/level set method[J].Journal of Computational and Applied Mathematics,2013,246: 251-259.
[10 ] MONAGHAN J J.Smoothed particle hydrodynamics and its diverse applications[J].Annual Review of Fluid Mechanics,2012,44: 323-346.
[11] LIU Moubin,LIU Guirong.Smoothed particle hydrodynamics(SPH):an overview and recent developments[J].Archives of Computational Methods in Engineering,2010,17(1): 25-76.
[12] SHAO Jiaru,LIU Moubin,YANG Xiufeng,et al.Improved smoothed particle hydrodynamics with RANS for free surface flow problem[J].International Journal of Computational Methods,2012,9(1): 1240001.
[13] MARRONE S,ANTUONO M,COLAGROSSI.δ-SPH model for simulating violent impact flows[J].Computer Methods in Applied Mechanics and Engineering,2011,200(13): 1526-1542.
[14] 杨秀峰,彭世镠.溃坝流的光滑粒子法模拟[J].计算物理,2010,272(2):173-180.(YANG Xiufeng,PENG Shiliu.Simulation of dam-break flow with SPH method[J].Chinese Journal of Computational Physics,2010,272(2):173-180.(in Chinese))
[15] LIU Moubin,SHAO Jiaru,CHANG Jianzhong.On the treatment of solid boundary in smoothed particle hydrodynamics[J].Science China Technological Sciences,2012,55(1): 244-254.
[16] BONET J,KULASEGARAM S.Correction and stabilization of smooth particle hydrodynamics methods with applications in metal forming simulations[J].International Journal for Numerical Methods in Engineering,2000,47(6): 1189-1214.
[17] MASCHEK W,MUNZ C D,MEYER L.Investigations of sloshing fluid motions in pools related to recriticalities in liquid-metal fast breeder reactor core meltdown accidents[J].Nuclear Technology,1992,98(1): 27-43.
Numericalstudyof3DfloodingflowusingSPHmethod
SHAOJiaru,YANGYu
(CollegeofMechanicalEngineering,ChongqingUniversityofTechnology,Chongqing400054,China)
In this paper, the SPH method is modified by incorporating a new coupled dynamic solid boundary with high calculation accuracy, in which non-penetrating condition is maintained within the particles and the free surface conditions are applied by using the sum of the support regions of corresponding particles. This method is expected to provide an accurate estimation of the rolling and broken effects of the water flow. A simplified flooding flow model is thus established to examine the effect of bulwark against the flood, in which various characteristics of the 3D flooding flow are well predicted. The collapse behavior of the cylindrical body of water is simulated using a 3D SPH model. The finding shows that the numerical results agree well with the experimental results, which demonstrates the effectiveness of the modified SPH method in modelling the free surface with violent flow behavior.
smoothed particle hydrodynamics (SPH), free surface, flood flow, coupled dynamic solid boundary
10.3876/j.issn.1000-1980.2017.06.007
2016-11-29
国家自然科学基金(11602045);重庆市基础科学与前沿技术研究项目(cstc2016jcyjA0373);重庆市教育委员会科学技术研究项目(KJ1600918)
邵家儒(1986—),男,山东淄博人,副教授,博士,主要从事光滑粒子动力学和流体力学研究。E-mail: shaojiaru@cqut.edu.cn
TV131.2
A
1000-1980(2017)06-0515-07

