黏聚单元嵌入技术及其在混凝土细观分析模型中的应用
吴贞杰,夏晓舟,章 青
(河海大学力学与材料学院,江苏 南京 211100)
黏聚单元嵌入技术及其在混凝土细观分析模型中的应用
吴贞杰,夏晓舟,章 青
(河海大学力学与材料学院,江苏 南京 211100)
采用针对随机颗粒的渐变网格剖分和黏聚单元嵌入的方案,建立骨料-砂浆-界面的三维高效细观有限元模型,并在单机上实现了混凝土标准试样的单轴拉伸和单轴压缩数值试验。结果表明:该嵌入方案能够捕捉到骨料-砂浆界面由弱连接到脱开的全过程,再现混凝土试样的破坏形态;通过对细观模拟结果获得的应力-应变关系曲线的对比分析,一定程度上揭示了混凝土宏观力学特性的内在机理,为探究混凝土类复合材料宏观力学特性的内在机制提供了技术保障。
混凝土;细观结构特征;黏聚单元;数值试验;宏观力学特性
混凝土是一种由骨料、砂浆以及二者之间的界面等构成的人工复合材料,其独特的细观结构(即颗粒的随机分布和界面的弱连接行为)决定了宏观上表现出与金属、陶瓷和聚合物等材料完全不同的拉压异性、剪胀性、非均匀强化和软化等力学特性。揭示这些力学特性的内在机理,以及如何在模型中体现这种独特的细观结构成为混凝土材料研究工作中的关键;混凝土有限元模型可以归纳为网格适应与不适应骨料边界2种。
适应边界的有限元模型,可以精细表现混凝土内部夹杂情况、界面形态。反映夹杂信息的模型主要有: Lattice model[1-2]、Random Aggregate model[3]、随机骨料模型[4-6]等,即从骨料级配、尺寸、形状等方面真实反映混凝土内部夹杂情况,对混凝土细观力学研究起到了推进作用。反映界面弱连接的建模方法有:网格投影法[5-7],将几何模型投影到结构性有限元网格中,由程序识别出各组分单元,该方法易导致界面呈齿状偏离实际;过渡单元法[8-10],直接离散预先设置一定厚度的骨料界面,该方法严重依赖单元形态易导致精度较差、单元数量庞大、过渡层厚度难以减小使得结果失真;过渡砂浆法[11],该方法设置高孔隙率砂浆作为过渡层,在力学参数方面做某种程度的等效,使得界面的力学行为仍是准确的;界面弹簧元法[12],在骨料-砂浆单元交界处建立由弹簧组成的重节点对来描述界面力学行为,该方法不能捕捉到材料失效后能量释放率;黏聚单元法[13-17],在模型所有单元上嵌入黏聚单元并用随机场定义本构参数,该方法反映了材料的异质性,又降低破裂路径对网格的依赖性。
不适应复杂边界的有限元模型,主要有随机力学模型[18],该模型存在对于骨料形状和级配对宏观力学性能的影响难以捕捉的问题;细观单元等效化模型[19],对在等效化的过程中,断裂能、强度等对组织敏感的物理量,简单套用细观力学理论还值得商榷。尽管如此,这些建模方法和理论研究都大大促进了混凝土细观数值试验的发展,并丰富了混凝土细观数值理论。
为了避免像大部分文献出现的计算规模超大且难在单机中运行的问题,也为了解骨料与砂浆之间接触连接的力学行为,笔者采用黏聚单元嵌入技术和渐变网格剖分的策略[20](界面近处密集远处稀疏的网格布局),在保证精度的同时可大大减小计算规模。
1 三维有限元建模技术
1.1 力-分离模式
模型界面处的黏聚单元采用力-分离模式描述其本构关系,力-分离模式下骨料界面任意一点,当该点应力满足二次应力准则时骨料和砂浆在该点处开始脱开,接着按照双线性关系演化。
二次应力准则公式为
(1)

为了更好地反映界面脱开过程中所遵循的机理,采用界面应力和界面相对位移来描述界面的变形响应。假定骨料界面黏聚-脱开效应满足双线性关系(界面2个切向s与t理论相同,这里只给出t的情况)如图1和图2所示,则
(2)

(3)
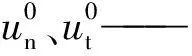
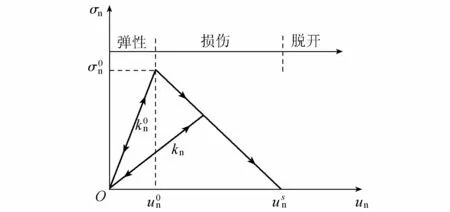
图1 界面法向应力与法向相对位移关系Fig.1 Stress-displacement curve of interface in the normal direction

图2 界面切向应力与切向相对位移关系Fig.2 Stress-displacement curve of interface in the tangential direction
1.2 建模步骤
1.2.1 骨料的随机生成
假定混凝土的骨料形状为球状,采用蒙特卡洛法在试样域中随机生成大量的抽样点,比如10万个,然后按由大到小的顺序进行骨料投放,后面投放的骨料是否有效,取决于与前面投放的颗粒是否重叠,若重叠,则视为无效,需继续随机投放,直至所有的颗粒投放完[4]。显然,越到后面的颗粒,投放的迭代次数越多,即投放效率越低。
1.2.2 初始网格的划分
混凝土初始网格的划分是指完成骨料、砂浆的四面体网格划分,为了不使网格规模超大,又能保证计算精度,采用渐变网格剖分程序[20],即引入径向稀疏渐变参数,实现在骨料边界上密集,远离边界的地方稀疏的网格布局。具体实施如下:
(a)在所有的骨料表面生成均匀的三角形面单元,然后设置稀疏渐变参数,采用四面体单元从骨料表面往球心稀疏过渡地离散骨料。(b)在混凝土试样表面生成三角形面单元,并和骨料表面单元形成封闭区域,然后检查生成的三角形面单元的法线方向,保证每一个面单元均指向砂浆域。(c)设置稀疏渐变参数,采用四面体单元从砂浆内向外表面稀疏过渡,离散整个砂浆区域。(d)删除表面三角形单元,合并骨料边界处的重结点,获得混凝土试样的三维细观有限元初始网格,如图3(a)所示。该初始网格仅仅体现了骨料的随机分布特征,对于骨料与砂浆之间的界面特征,则需要在骨料和砂浆之间嵌入一层黏聚界面单元才能反映。
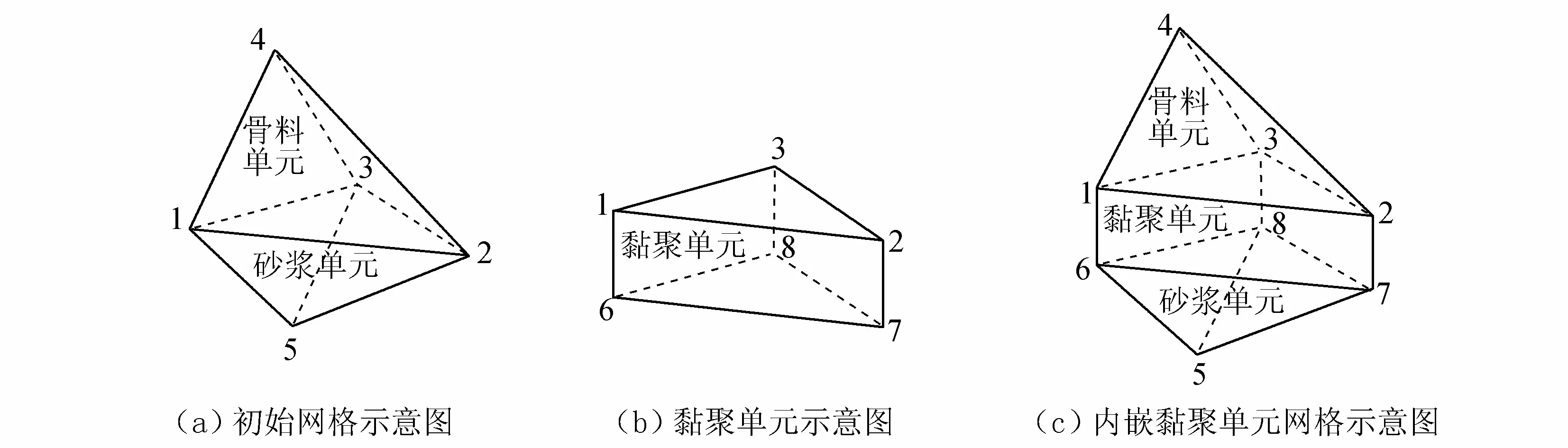
图3 黏聚单元的生成Fig.3 The generation of cohesive element
1.2.3 黏聚界面单元的嵌入
骨料边界处采用无厚度的六结点黏聚界面单元离散,该单元上下底面结点按照逆时针顺序编号,如图3(b)所示。由于骨料边界处的单元与对应边界处的砂浆单元共享3个结点,故将此3个结点按照逆时针方向排列,作为六结点黏聚单元单侧的结点;原地复制形成另一侧的结点坐标,并将复制出的结点重新编号,形成黏聚单元结点信息(图3(b)),图3(c)即为该建模技术生成的含无厚度黏聚界面单元网格示意图。其中,黏聚界面单元的嵌入是通过计算机编程实现的,具体算法在1.3节中详细介绍。
1.3 黏聚单元嵌入算法
黏聚单元的生成过程,简言之就是对混凝土骨料、砂浆四面体单元信息进行加工;搜索两种单元的公共结点,并以此为基础嵌入黏聚单元的过程。该算法主要分为数据准备、分区搜索、结点定向排序和黏聚单元的生成4个部分。
1.3.1 数据准备
界面单元嵌入算法需要的数据有:球体骨料的几何信息、初始网格结点、单元信息。
球体骨料几何信息包括骨料编号、球心坐标和粒径;结点信息包括结点编号、坐标及其所在的骨料编号(若为砂浆结点则骨料编号为0),其中,结点所在的骨料编号,可由结点到骨料球心的距离与该骨料半径的相对误差确定,若相对误差小于0.001,则该骨料为此结点所在的骨料;单元信息包括单元编号、材料编号、结点编码和1.3.2节分区搜索用到的子域编号。
1.3.2 分区搜索

图4 模型分区示意图Fig.4 The subdomains of numerical specimen
黏聚单元嵌入算法用到了求解域分区和材料分区相结合的搜索方法。首先,为提高相关单元的搜索效率,把整个求解域划分成若干个子区域,然后在各自的子区域进行搜索,显然网格规模越大,子区域划分越多,搜索效率就越高,对于三维细观有限元模型,规模至少十几万个单元,分区搜索显得很必要,因此,单元信息中还需加入所属的子域编号。按象限将有限元模型中的结点划分成8个分区,然后由附着在象限域中结点上的单元构成单元子区域,因此,各单元子域存在重叠区(图4)。
由于黏聚单元的结点一半位于骨料区域、一半位于砂浆区域,见图3(c),故借助材料分区策略,以骨料单元为参照,搜索与其共有3个结点的砂浆单元。具体步骤如下:判断骨料单元是否存在3个结点落在骨料球面上,若存在,则这3个结点为黏聚单元的一侧结点;根据上述确定的3个界面结点,在所属的单元子区域内进行相关砂浆单元的搜索,并对砂浆单元中的共点结点进行原位复制,复制的结点码由初始网格的结点总数往后编排。
1.3.3 结点定向排序
图5 黏聚结点定向Fig.5 Orientations of cohesive nodes

图6 混凝土试样内部组成的网格展示Fig.6 The components mesh of the concrete specimen
由于黏聚单元上下底的结点逆时针围绕,故需将搜索得到的结点重新排序。假设i、j、k结点为搜索得到的公共结点,如图 5所示,通过向量r1和r2的叉积得出围成的三角形法线r3;并依据r3与r4所成夹角θ判断i、j、k的旋转方向。若θ为锐角,则i、j、k为逆时针方向;反之,为顺时针方向,需要将j、k的顺序调换。其中,r1为i结点指向j结点的向量;r2为j结点指向k结点的向量;r4为i结点指向球体骨料形心的向量。
1.3.4 黏聚单元的生成
黏聚单元中靠骨料一侧的结点按逆时针排列,构成前3个结点,靠砂浆的一侧由复制的结点按逆时针排列,构成后3个结点;同时将相关的砂浆单元结点编码进行调整,即把重结点替换成复制的结点,完成三维混凝土黏聚界面单元的嵌入,如图3(c)所示。图6为混凝土立方和圆柱2种试样内部组成的网格展示图,其中黏聚单元覆盖整个骨料表面,起到连接骨料单元和砂浆单元的作用,可模拟界面的脱开和滑移等复杂变形特征。
2 混凝土标准试块数值试验
2.1 标准试样的细观有限元模型
某二级配混凝土标准试样(150 mm×150 mm×150 mm),粗骨料(粒径为27 mm)为29个,细骨料(粒径12 mm)为498个,在含随机骨料分布的立方几何模型基础上,采用本文提出的网格建模技术生成混凝土标准试样的细观有限元模型,生成的结点总数为36 423,单元总数为151 820,其中四面体单元个数为129 490、黏聚界面单元个数为22 330,如图7所示。

图7 混凝土立方试样Fig.7 The cube specimen for concrete
假定骨料为线弾性体,即不发生损伤破坏,其杨氏模量为57 GPa、泊松比为0.2;水泥砂浆采用损伤塑性本构模型,其杨氏模量为29 GPa、泊松比为0.2,砂浆拉伸和压缩的损伤变量(D)随应变(ε)的演化规律分别如图8(a)、8(b)所示;黏聚单元采用1.1节中介绍的力-分离模式本构模型,其法向刚度和切向刚度分别取为1.4×106MPa/mm和1×106MPa/mm,断裂能取0.03 N/mm。

图8 砂浆损伤演化关系Fig.8 The damage evolution of mortar matrix
采用动力隐式算法对整个细观有限元模型进行损伤破坏的全过程计算,探究混凝土试样在轴向拉伸和压缩情况下的力学行为,以验证本文提出的混凝土细观有限元建模技术的可靠性与高效性。
2.2 单轴拉伸结果分析
如图7(a)所示,将混凝土标准试样底面各结点固定,采用位移加载方式,在顶面各结点逐步施加竖直向上的位移荷载。试样拉伸损伤计算结果如图9所示(图中黑色区域代表球体骨料);界面单元刚度退化情况如图10所示;宏观拉伸应力-应变曲线如图11所示,并与砂浆拉伸应力-应变全曲线图做对比分析。

图9 拉伸损伤分布Fig.9 Damage distribution under uniaxial tensile action
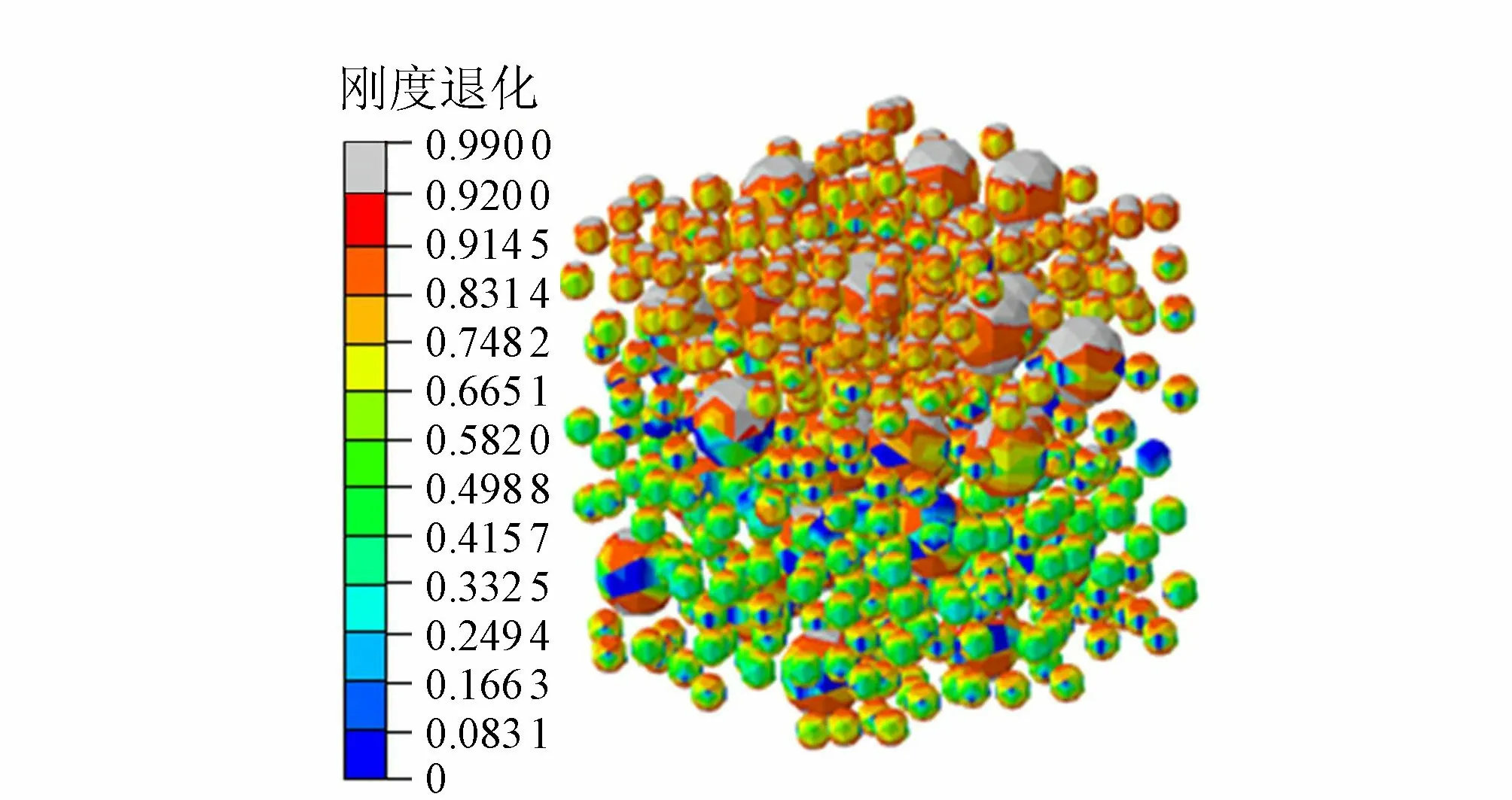
图10 拉伸界面刚度退化分布Fig.10 Scalar stiffness degradation distribution of interface under uniaxial tension
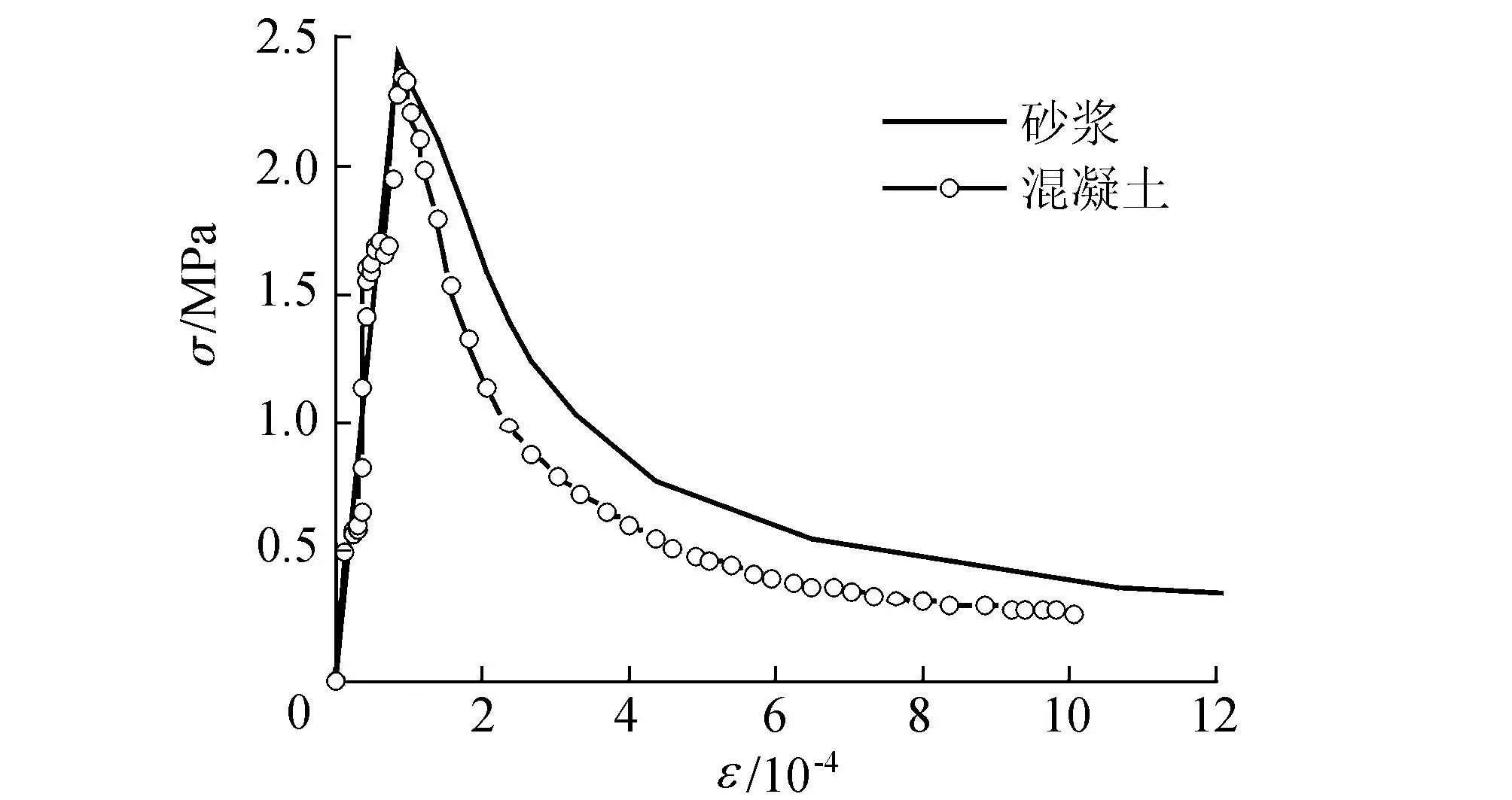
图11 单轴拉伸应力-应变曲线对比Fig.11 The stress-strain curves under uniaxial tension
取出3个荷载步下的截面损伤分布如图9所示,可以看出损伤区域按层状分布,越靠近试块顶端损伤值越大。向上拉伸至位移为0.013 mm(图9(a))时,模型损伤开始出现,分布特征不明显;位移为0.018 mm(图9(b))时,模型损伤层状分布明显,同时黏聚界面开始分离、损伤演化速度加快并开始向模型表面扩展;位移为0.282 mm( 图9(c))时,模型整体损伤明显,损伤值最大区域界面分离明显,损伤速度趋近平缓。再单独提取界面单元刚度退化图(图10),可知黏聚界面单元刚度退化也呈层状分布,且越靠近顶部刚度退化越快;单个骨料上界面单元按先上下后四周的顺序刚度退化。
总体可以看出,拉损伤呈横断分布且损伤路径发生在骨料界面区域并沿之扩展,这是因为界面的力学性能相对于基体和颗粒而言要低,同时也是因为颗粒对损伤发展存在抑制和路径偏转作用,而且大颗粒表面较小颗粒有着更强的作用:最初拉损伤集中萌发在试块顶部,扩展时在细骨料两侧路径稍稍偏转;当遇到粗骨料时,由于粗骨料有明显的抑制作用,左右两侧的损伤路径明显偏转,有时也会出现两条损伤路径汇合的情况。就这样,损伤路径在沿着粗、细颗粒不断偏转或汇合之后,最终留下一道道连着骨料类似“项链”的拉损伤带。
将数值试验所得的混凝土拉伸应力-应变曲线与砂浆拉伸全曲线作对比(图11):上升段,两者曲线十分吻合、抗拉强度(峰值)近似相等;下降段,混凝土的应力-应变曲线较砂浆下降得更为陡峭,这是由于界面的力学性质相对砂浆而言(尤其强度和断裂能)十分薄弱,即力学性质较弱的界面层降低了混凝土的韧性。
2.3 单轴压缩结果分析
将图7(a)的荷载形式改为竖直向下的位移加载模式,以研究混凝土轴向压缩的力学行为。试样压剪损伤和拉伸损伤分布,如图12所示;黏聚界面单元刚度退化如图13所示;由细观计算结果提取出来的混凝土压缩应力-应变曲线(图14),并将其与砂浆压缩应力-应变全曲线图做对比。
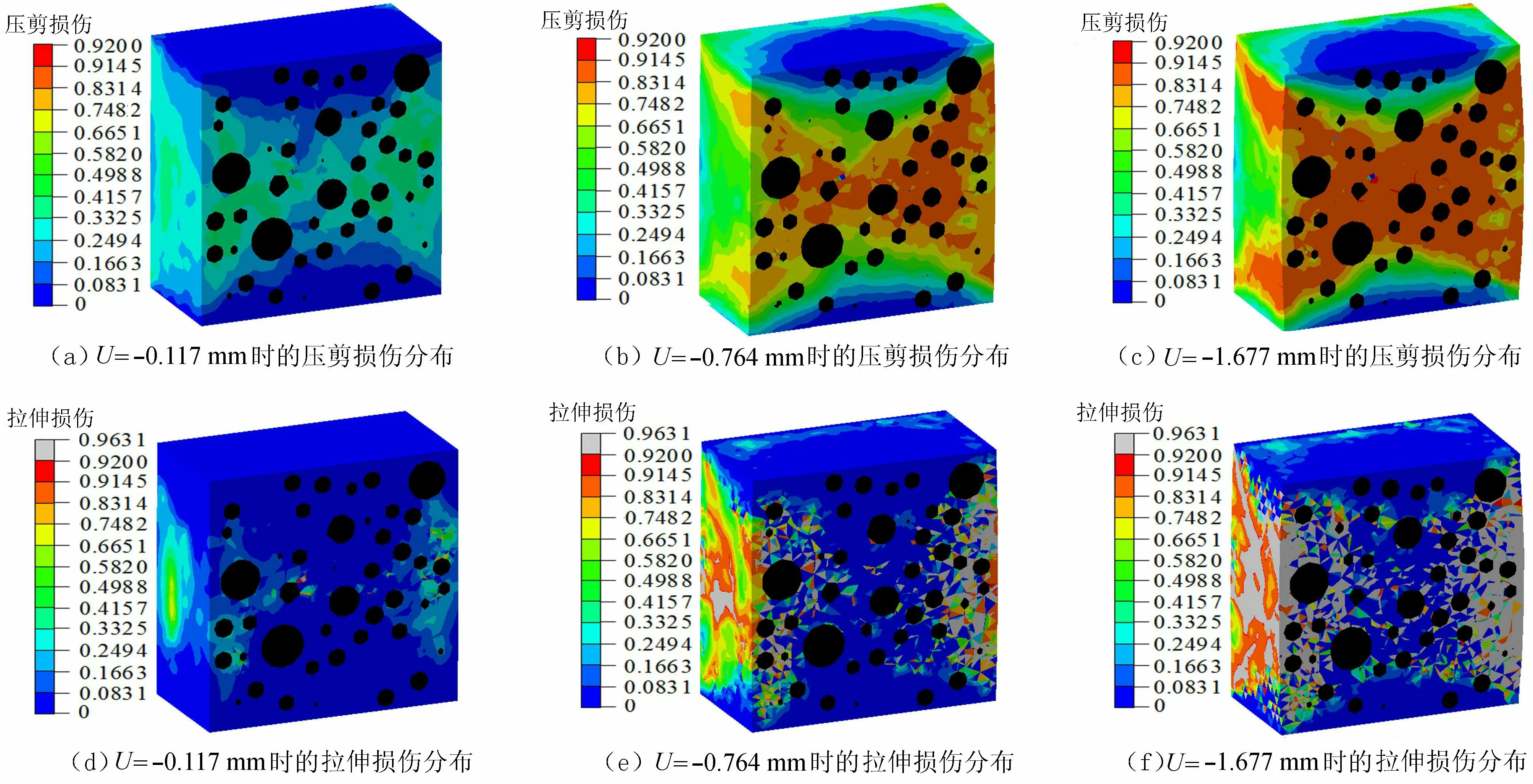
图12 单轴压缩下混凝土的损伤分布Fig.12 The damage distribution within the concrete under uniaxial compression
提取3个荷载步下的截面压剪损伤和拉伸损伤分布图(图12),可以看出压缩至位移(U)为0.117 mm时压剪损伤开始出现,呈X形双剪分布,拉损伤则集中于试样边缘;位移为0.764 mm时,剪胀现象开始出现、损伤演化速度较快并开始向试样外侧演化,且外侧明显出现剥落现象;位移为1.677 mm时,剪胀现象明显、X形压剪损伤演化速度趋于平缓,但外侧剥落严重,呈现最终破坏形式。该混凝土数值试验的压缩破坏形态(图12(c)),与文献[21]中混凝土真实压缩破坏形态(图15) 基本一致。再提取界面单元刚度退化图(图13),看出单元按先两侧后上下的方式退化,且图12双剪破坏区域对应的界面单元刚度最先退化、上下区域的界面单元呈漏斗状退化。

图13 压缩界面刚度退化分布Fig.13 Scalar stiffness degradation distribution of interface under uniaxial compression

图15 混凝土压缩破坏形态Fig.15 The failure mode under uniaxial compression for concrete sample
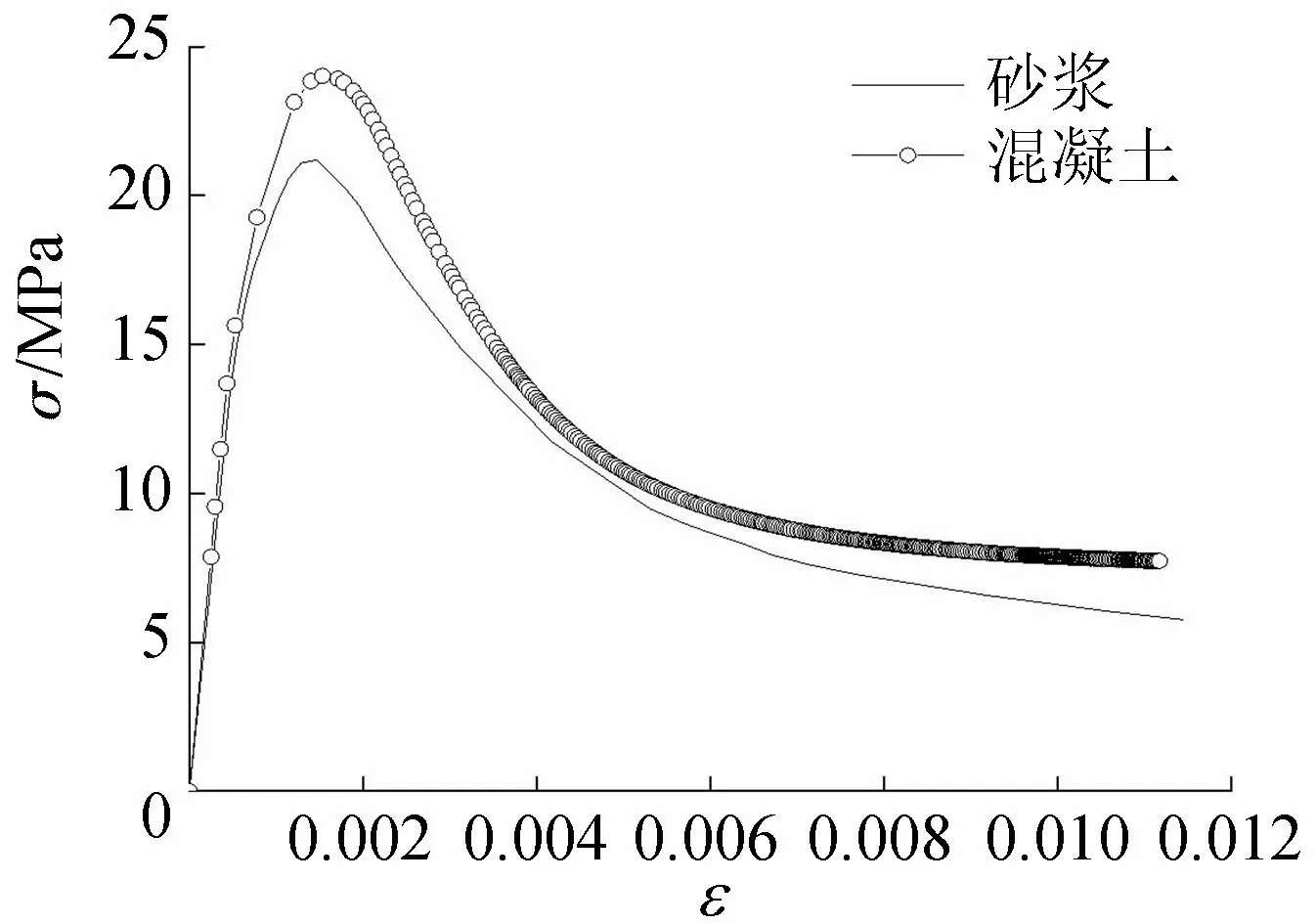
图14 单轴压缩应力-应变曲线对比Fig.14 The stress-strain curves under uniaxial compression
总体可以看出,压缩荷载下损伤主要呈压剪形式并逐步往斜带贯穿的破坏模式发展;骨料界面的脱开也以剪切为主,且分布在骨料边缘的左右两侧,由于大骨料对剪切也有一定的抑制作用,骨料界面的滑移最先出现在沿左斜带发展的骨料边缘上。而最终混凝土试块呈现明显的X形双剪破坏形式,是因为在三维模型中大骨料的颗粒数较多且分布均匀,促使试块左右两侧的剪切带损伤演化的发展机会均衡导致的。
最后对比数值试验压缩应力-应变曲线与砂浆压缩全曲线(图14),可以看出上升段混凝土的抗压强度明显大于砂浆峰值;下降段两者趋势较为接近,但混凝土的残余强度比砂浆强。由图11和图14得该数值试验下混凝土的最大拉应力为2.36 MPa、最大压应力为24.02 MPa,符合真实情况下混凝土拉伸、压缩应力极值范围,也满足混凝土抗压强度较抗拉强度大一个数量级的关系[22],由此可验证该数值试验结果的可靠性。
3 结 论
a. 分区搜索大大提高了黏聚界面单元的生成效率,且随着初始网格规模的增大,效率提高越明显。
b. 渐变网格剖分的策略,不仅保证界面上的黏聚单元足够的密集,而且相比于过渡单元[8-10]的方法,能够有效地降低三维网格的计算规模,使得在单机上的模拟结果能满足精度上的要求。
c. 采用界面黏聚单元处理骨料边界,较薄层单元[9]更接近骨料与砂浆的界面黏结行为;另外也弥补了界面弹簧元法[12]不能获取材料失效后能量释放率的不足,单轴拉伸和压缩的计算结果进一步验证了这种模式的可靠性和有效性。
因此,基于界面黏聚单元的随机颗粒分布的有限元建模技术,为揭示颗粒型复合材料的宏观力学特性的内在机理提供了最有效的技术支持,可通过它探究颗粒界面的不同力学行为(包括界面厚度、界面耦合本构[23])对材料宏观力学特性的影响规律以及尺寸效应的本质规律;除此之外,还可以通过它进一步探究混凝土温湿效应[24]、断裂行为[25]以及最佳颗粒级配理论等问题,为颗粒型复合材料的微结构设计提供指导。
[ 1 ] SCHLANGEN E, VAN M J G M. Simple lattice model for numerical simulation of fracture of concrete materials and structures[J]. Materials and Structures, 1992, 25(9): 534-542.
[ 2 ] WANG L C, UEDA T. Meso-scale modeling of chloride diffusion in concrete with consideration of effects of time and temperature[J].Water Science and Engineering, 2009, 2(3): 58-70.
[ 3 ] MOHAMED A R, HANSEN W. Micromechanical modeling of concrete response under static loading-part 1:model development and validation[J].ACI Materials Journal, 1999, 96(2): 196-203.
[ 4 ] 夏晓舟, 章青, 汤书军.混凝土细观损伤破坏过程的数值模拟[J].河海大学学报(自然科学版), 2007, 35(3): 319-325.(XIA Xiaozhou, ZHANG Qing, TANG Shujun. Numerical simulation and the meso-damage process for concrete material[J]. Journal of Hohai University(Natural Sciences), 2007, 35(3): 319-325.(in Chinese))
[ 5 ] 刘光廷, 王宗敏. 用随机骨料模型数值模拟混凝土材料的断裂[J]. 清华大学学报(自然科学版), 1996, 36(1): 84-89.(LIU Guangting, WANG Zongmin. Numerical simulation study of fracture of concrete material using random aggregate model[J]. Jounal of Tsinghua University(Sci amp; Tech), 1996, 36(1): 84-89.(in Chinese))
[ 6 ] 方秦, 张锦华, 还毅, 等. 全级配混凝土三维细观模型的建模方法研究[J]. 工程力学, 2013, 30(1): 14-21.(FANG Qin, ZHANG Jinhua, HUAN Yi, et al. The investigation into three-dimensional mesoscale modelling of fully-graded concrete[J]. Engineering Mechanics, 2013, 30(1): 14-21.(in Chinese))
[ 7 ] 马怀发, 陈厚群, 黎保琨. 混凝土试件细观结构的数值模拟[J]. 水利学报, 2004, 35(10): 27-35.(MA Huaifa, CHEN Houqun, LI Baokun. Meso-structure numerical simulation of concrete specimens[J]. Journal of Hydraulic Engineering, 2004, 35(10): 27-35.(in Chinese))
[ 8 ] 应宗权, 杜成斌. 考虑界面影响的混凝土弹性模量的数值预测[J]. 工程力学, 2008, 25(8): 92-96.(YING Zongquan, DU Chengbin. A Numerical method for effective elastic modulus of concrete with interfacial transition zone[J]. Engineering Mechanics, 2008, 25(8): 92-96.(in Chinese))
[ 9 ] 汤书军. 混凝土材料细观力学模型与破坏分析[D]. 南京: 河海大学, 2006.
[10] 马怀发, 陈厚群, 吴建平, 等. 大坝混凝土三维细观力学数值模型研究[J]. 计算力学学报, 2008, 25(2): 241-247.(MA Huaifa, CHEN Houqun, WU jianping, et al. Study on numerical algorithm of 3D meso-mechanics model of dam concrete[J]. Chinese Journal of Computational Mechanics, 2008, 25(2): 241-247.(in Chinese))
[11] 杜修力, 金浏. 考虑过渡区界面影响的混凝土宏观力学性质研究[J]. 工程力学, 2012, 29(12): 72-79.(DU Xiuli, JIN Liu. Research on the influence of interfacial transition zone on the macro-mechanical properties of concrete[J]. Engineering Mechanics, 2012, 29(12): 72-79.(in Chinese))
[12] 王娟, 李庆斌, 卿龙邦, 等. 混凝土单轴抗压强度三维细观数值仿真[J]. 工程力学, 2014, 31(3): 39-44.(WANG Juan, LI Qingbin, QING Longbang, et al. 3D simulation of concrete strength under uniaxial compressive load[J]. Engineering Mechanics, 2014, 31(3): 39-44.(in Chinese))
[13] YANG Z J, SU X T, CHEN J F, et al. Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials[J]. International Journal of Solids and Structures, 2009, 46: 3222-3234.
[14] SU X T, YANG Z J, LIU G H. Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials: a 3D study[J]. International Journal of Solids and Structures, 2010, 47: 2336-2345.
[15] YIN A, YANG X H, GAO H, et al. Tensile fracture simulation of random heterogeneous asphalt mixture with cohesive crack model[J]. Engineering Fracture Mechanics, 2012, 92: 40-55.
[16] YIN A, YANG X H, YANG Z J. 2D and 3D fracture modeling of asphalt mixture with randomly distributed aggregates and embedded cohesive cracks[J].Sci Verse Science Direct, 2013, 6: 114-122.
[17] WANG X F, YANG Z J, ANDREY P J. Monte Carlo simulations of mesoscale fracture of concrete with random aggregates and pores: a size effect study[J].Construction and Building Materials, 2015, 80: 262-272.
[18] 唐春安, 朱万成. 混凝土损伤与断裂:数值试验[M]. 北京: 科学出版社, 2003: 24-79.
[19] 杜修力, 金浏. 用细观单元等效化方法模拟混凝土细观破坏[J].土木建筑与环境工程, 2012, 34(6): 1-7.(DU Xiuli, JIN Liu. Simulation of concrete meso-failure process with meso element equivalent method[J]. Journal of Civil, Architectural amp; Environmental Engineering, 2012, 34(6): 1-7.(in Chinese))
[20] 夏晓舟, 陈爱玖, 刘锋, 等. 基于渐变网格剖分方法的再生混凝土细观数值试验[J]. 中山大学学报(自然科学版), 2008, 47(增刊2): 14-17.(XIA Xiaozhou, CHEN Aijiu, LIU Feng, et al. Meso-numerical experiment of recycle concrete based on gradually mesh division scheme[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2008, 47(Sup 2): 14-17.(in Chinese))
[21] 闫东明. 混凝土动态力学性能试验与理论研究[D].大连: 大连理工大学, 2006.
[22] 中华人民共和国住房和城乡建设部,国家质量监督检验检疫总局:混凝土结构设计规范GB50010—2010[S].北京: 中国建筑工业出版社, 2010.
[23] IDIART A E, LOPEZ C M, CAROL I. Chemo-mechanical analysis of concrete cracking and degradation due to external sulfate attack: a meso-scale model[J].Cement amp; Concrete Composites, 2011, 33: 411-423.
[24] HAI Y, ZHU Y M. Mesocosmic study on autogenous shrinkage of concrete with consideration of effects of temperature and humidity[J].Water Science and Engineering, 2009, 2(4): 85-94.
[25] 吴建营, 李锋波, 徐世烺. 混凝土破坏全过程分析的扩展内嵌裂缝模型[J].水利水电科技进展, 2016, 36(1):53-59.(WU Jianying, LI Fengbo, XU Shilang. Extended embedded crack finite element method for modeling localized failures in concrete structures[J].Advances in Science and Technology of Water Resources, 2016, 36(1):53-59.(in Chinese))
Embeddingtechniqueofcohesiveelementanditsapplicationinconcretemirco-levelanalysismodel
WUZhenjie,XIAXiaozhou,ZHANGQing
(CollegeofMechanicsandMaterials,HohaiUniversity,Nanjing211100,China)
By adopting gradually tetrahedral meshing technique for random distributed aggregates and embedding scheme of cohesive element, a high efficiency 3D aggregate-mortar-interface meso finite element model is established, in which the uniaxial tension and uniaxial compression experiments of concrete cube samples are carried out in single computer. The numerical result shows that the whole process from weak connection to separation between aggregates and mortar is readily captured, which reproduces the failure mode of concrete specimens. The inner mechanism of the macro-mechanical properties of concrete is thus revealed by comparing the computed stress-strain curves from uniaxial tension and compression experiments, which is supposed to provide a technical support to explore the inner mechanism of concrete like composite materials.
concrete; micro structure characteristics; cohesive element; numerical experiments; macro-mechanical properties
10.3876/j.issn.1000-1980.2017.06.010
2016-12-10
国家自然科学基金(11132003,11372099);中央高校基本科研业务费专项(2013B32714)
吴贞杰(1993—),女,江苏南通人,硕士研究生,主要从事工程材料和结构的破坏力学行为研究。E-mail: wuzhenjiePaige@163.com
夏晓舟,副教授。E-mail: xiaxiaozhou@163.com
TU528.1
A
1000-1980(2017)06-0535-08

