考虑零注入约束的双线性WLAV状态估计
沈甜甜,黄启建,吴常胜,孙国强,卫志农,臧海祥
(1.河海大学能源与电气学院,江苏 南京 210098; 2.国网池州供电公司,安徽 池州 247000)
考虑零注入约束的双线性WLAV状态估计
沈甜甜1,黄启建2,吴常胜2,孙国强1,卫志农1,臧海祥1
(1.河海大学能源与电气学院,江苏 南京 210098; 2.国网池州供电公司,安徽 池州 247000)
零注入节点功率失配量对电力系统安全评估有着重要影响,为减小零注入节点的功率失配量,提出了考虑零注入约束的双线性WLAV(Weighted Least Absolute Value)状态估计方法,该方法将零注入约束以等式约束的形式添加到双线性WLAV状态估计中。基于IEEE标准系统,采用零注入约束的双线性WLAV状态估计方法对国内某省网进行仿真,结果表明:该方法既能保留基于内点法的双线性WLAV状态估计原有的计算效率高的优点,又能减小零注入节点的功率失配量,且抗差性能有一定程度的提升。
电力系统;状态估计;零注入;等式约束;内点法;失配量
电力系统状态估计[1-6]是能量管理系统中的核心基础模块,准确的状态估计结果能为现代电网的实时分析、控制提供保障。实际电力系统中存在许多零注入节点,理论上零注入节点的注入功率严格为零[7-9],然而由于状态估计的量测误差、模型参数误差等原因,状态估计下零注入节点功率往往不为零,导致这些节点上的状态估计结果不能满足潮流方程[7],影响后续的安全评估结果,因此如何保证状态估计结果更好地符合零注入约束值得深入研究。
目前研究比较广泛的处理零注入约束的方法主要有大权重法[1-3]和拉格朗日乘子法[10]。传统的大权重法将零注入节点的注入功率当作精确的量测量,赋以较大的权重参与状态估计计算。拉格朗日乘子法是将零注入约束作为等式约束,采用拉格朗日乘子法求解。大权重法形式简洁,在现有状态估计程序上可直接应用,但这种方法会严重劣化信息矩阵条件数,增加计算负担,甚至造成状态估计程序的不收敛。当零注入节点的比例很高时,拉格朗日乘子法将导致信息矩阵规模显著增大,影响状态估计的效率,但可极大地提高求解的稳定性和精确性。Hachtel增广矩阵法[11]和Cholesky分解法[12]等都是在这方面的尝试。
加权最小绝对值(Weighted Least Absolute Value, WLAV)是一种研究广泛的抗差状态估计方法[13-14],该方法模型中可计及等式约束[15],采用内点法,并引入拉格朗日乘子求解,但非线性内点法的计算效率难以满足工程需求。文献[16]用变量代换方法,将状态估计问题分解为两步线性化过程,提出了双线性WLAV抗差估计,该方法与传统的WLAV状态估计相比精度略有降低,但运算效率有显著提升。由于该方法没有考虑零注入约束,应用于实际系统时将产生较大的零注入节点功率失配量,影响电力系统的安全评估。
本文以双线性WLAV状态估计为基础,结合零注入节点注入功率严格为零的特点,将零注入约束作为等式约束引入双线性WLAV状态估计的第一步线性方程中,用内点法求解,可以有效减小零注入节点的功率失配量,用IEEE标准系统以及国内某实际省网的仿真结果验证了所提方法的实用性及有效性。
1 变量代换模型
电力系统状态估计属于非线性优化问题,其量测方程可表示为
z=h(x)+ε
(1)
式中:z——量测向量;x——状态向量;h(x)——非线性函数;ε——量测误差向量。
结合电力系统的特性,通过引入中间变量可将非线性方程(1)分解为[16]
z=Cy+ε
(2)
y′=f(y)
(3)
y′=Dx′+εy′
(4)
x=t(x′)
(5)
式中:y、y′、x′——中间变量;f(y)、t(x′)——非线性函数;C、D——常系数矩阵;εy′——中间变量y′的误差向量。
状态估计量测量包括节点电压量测、节点功率量测、支路功率量测,在极坐标系下,其计算方程为
(6)
式中:Ui、Pi、Qi——节点i的电压幅值,注入有功及无功功率;Pij、Qij——支路ij上的有功和无功功率;Gij、Bij——节点i和节点j之间的互电导和互电纳;gij、bij、yc——支路ij的π形等效电路的串联电导、串联电纳和对地电纳;θij——支路两端相角差,θij=θi-θj。
取中间变量y为
(7)
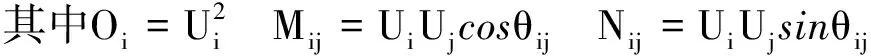
代入式(6)可得
(8)
式中:Gii、Bii——节点i的自电导和自电纳。
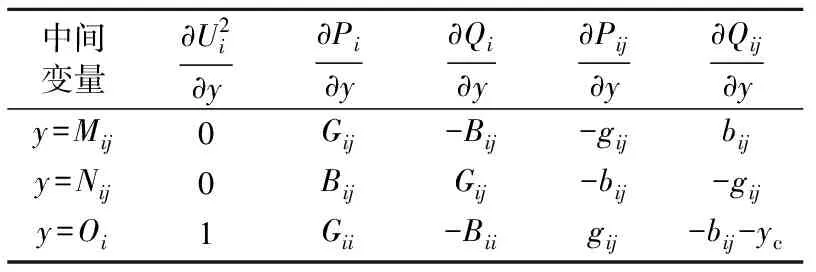
表1 常系数矩阵C
由式(8)可得C矩阵的各元素值如表1所示。
令式(3)中的非线性函数为
(9)
将式(7)所得的y带入式(9)中即可求得y′。令中间变量x′为
x′=[lnUθ]T
(10)
式中:U——节点电压幅值向量;θ——节点电压相角向量。
可建立y′与x′之间的线性方程:
(11)
式中:I——单位矩阵;S——节点关联矩阵;Sr——去掉平衡节点的节点关联矩阵。
求出x′后可由下式求出x:
x=[eln(U)θ]T
(12)
2 带等式约束的双线性WLAV状态估计
上述双线性WLAV状态估计未考虑零注入约束,估计结果不能满足零注入节点功率为零的条件。考虑到零注入节点的注入功率严格为零,可将零注入约束以等式约束的形式添加到双线性WLAV状态估计的第一步中。带等式约束的WLAV模型为
(13)
式中:g(y)=0——零注入节点的等式约束;l、n——松弛变量。
构造出式(13)的拉格朗日函数:
L=wT(l+n)-ηT(z-Cy+l-n)-αTl-βTn-λTg(y)
(14)
式中:α、β、λ、η——拉格朗日乘子。
由式(13)的KKT(Karush-Kuhn-Tucker)条件可得如下KKT方程:
(15)
式中:A、B、L、N——以α、β、l、n为对角元素的对角阵;μ——扰动因子。
应用牛顿法解如上KKT方程,可得修正方程:
-CTdη+g(y)Tdλ+2g(y)Tλdy=-Ly
(16)
-Cdy+dl-dn=-Lη
(17)
-dη-dα=-Ll
(18)
dη-dβ=-Ln
(19)
(20)
(21)
(22)
取初值η=0,α=β=w则Ll=Ln=0,则式(18~21)可化为
(23)
将式(23)代入式(16~17),并联立式(22),可得到修正方程的矩阵形式:
(24)

3 算 例 测 试
为测试本文所提出的考虑零注入约束的双线性WLAV状态估计的性能,对多个节点系统算例,包含IEEE14与IEEE118节点系统以及华东某省网(含736个节点),进行测试分析。算例测试包含双线性WLAV状态估计、大权重法(用双线性WLAV求解)以及考虑零注入约束的双线性WLAV状态估计3种方法,下文分别用方法1、2、3来代指这3种方法。在量测配置方面,方法1的量测数据不包含零注入节点功率量测,方法2的零注入节点功率量测的权值取为同类量测的10倍,其余相同。
量测值由潮流真值叠加正态分布误差获得,节点电压量测的误差标准差为0.005,功率量测的误差标准差为0.01,权重取方差的倒数。各个方法的收敛判据设置相同。
3.1 基本测试
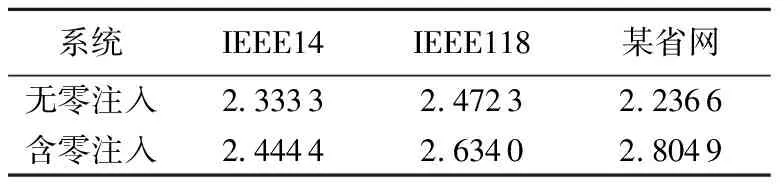
表2 各节点系统的量测冗余度
为测试本文所提方法的计算精度以及在减小零注入节点功率失配量方面的效果,比较了多个算例下3种方法的估计效果。各测试系统的量测冗余度如表2所示。各测试系统下3种方法的估计结果如表3所示。
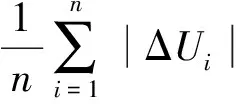
3.2 抗差性测试
为测试3种方法在不同比例坏数据情况下的抗差效果,基于IEEE57节点系统添加不同比例的坏数据,各比例坏数据情况随机构造多组独立算例组,用平均误差及最大误差来衡量状态估计的抗差效果。
由图1可看出,随着坏数据比例的逐渐增大,3种算法的估计误差都是越来越大。图1(a)中,在坏数据比例较低时,方法2与方法3的抗差效果对比方法1已显现出一定的优势,而随着坏数据比例的增大,二者的优势更为明显;图1(b)可直观地看出方法3的抗差效果优于方法1和方法2;图1(c)中,3种方法的估计误差较为接近,方法3的估计误差受坏数据比例增大的影响最小,可见其抗差效果最好;图1(d)中,3种方法误差值增长趋势大致相同,但方法3的误差值较小。由此可以看出,本文所提出的考虑零注入约束的双线性WLAV状态估计的抗差性最好。

表3 电力系统的状态估计结果
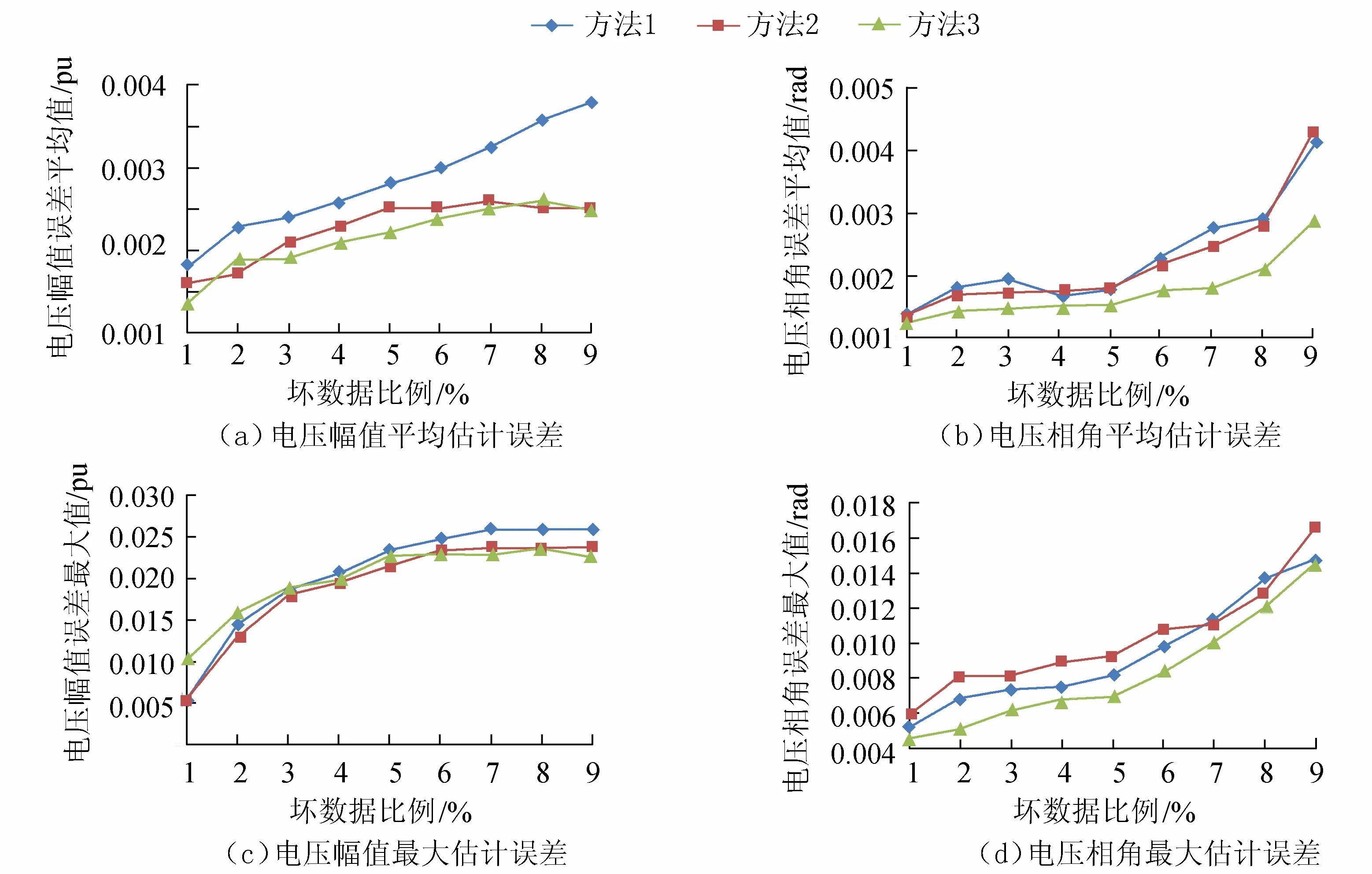
图1 IEEE57节点系统估计误差Fig.1 The estimation error for IEEE57 node system
3.3 效率测试
为了对本文方法的迭代次数及计算效率进行测试,分别用IEEE标准系统及一实际省网进行了算例测试,测试结果如表4所示,方法1、2和3即前文所提及的3种方法,其中迭代次数一列的2个数值分别表示双线性第一步和第二步的迭代次数,方法4为非线性内点法WLAV状态估计,所用量测数据不含零注入节点功率量测。由表4的数据可以看出,本文方法由于添加了等式约束,提高了矩阵阶数,计算量有所增加,因而计算效率难免有所下降;然而相比于非线性状态估计而言,所提计及零注入的双线性WLAV状态估计方法计算效率仍然占优。

表4 不同系统的迭代次数和计算时间
4 结 语
本文提出了考虑零注入约束的双线性WLAV状态估计方法,与不考虑零注入约束的双线性WLAV相比,估计结果准确性略有降低,但能有效减小零注入节点的功率失配量,且在考虑坏数据比例的测试中,本文方法有较好的抗差性。由于添加了等式约束,在运算效率方面有所降低,但本文方法同样不需要计算海森矩阵,因此仍有较高的计算效率。本文方法有效改善了零注入节点的估计效率,从而为后续的安全评估提供了保障。
[ 1 ] SCHWEPPE F C,WILDES J.Power system static-state estimation,part I:exact model[J].IEEE Transactions on Power Apparatus and Systems,1970,89(1):120-125.
[ 2 ] SCHWEPPE F C,ROM D B.Power system static-state estimation,part II:approximate model[J].IEEE Transactions on Power Apparatus and Systems,1970,89(1):125-130.
[ 3 ] SCHWEPPE F C.Power system static-state estimation,part III:implementation[J].IEEE Transactions on Power Apparatus and Systems,1970,89(1):130-135.
[ 4 ] 叶芳,卫志农,孙国强,等.基于自动微分技术的多平衡机状态估计算法[J].河海大学学报(自然科学版),2012,40(2):233-237.(YE Fang,WEI Zhinong,SUN Guoqiang,et al.State estimation algorithm for multi-balancing machines based on automatic differentiation technology[J].Journal of Hohai University(Natural Sciences),2012,40(2):233-237.(in Chinese))
[ 5 ] HOLTEN L,GJELSVIK A,AAM S,et al.Comparison of different methods for state estimation[J].IEEE Transactions on Power Systems,1988,3(4):1798-1806.
[ 6 ] 孙国强,朱超,卫志农,等.基于综合集成赋权法的输电线路动态综合评估[J].河海大学学报(自然科学版),2016,44(3):272-277.(SUN Guoqiang,ZHU Chao,WEI Zhinong,et al.Dynamic comprehensive evaluation of transmission lines based on integrated weighting method[J].Journal of Hohai University (Natural Sciences),2016,44(3):272-277.(in Chinese))
[ 7 ] 郭烨,张伯明,吴文传,等.直角坐标下含零注入约束的电力系统状态估计修正牛顿法[J].中国电机工程学报,2012,32(19):96-100.(GUO Ye,ZHANG Boming,WU Wenchuan,et al.Power system state estimation solution with zero injection constraints using modified newton method[J].Proceedings of the CSEE,2012,32(19):96-100.(in Chinese))
[ 8 ] 郭烨,吴文传,张伯明,等.极坐标下含零注入约束的电力系统状态估计的修正牛顿法与快速解耦法[J].中国电机工程学报,2012,32(22):113-117.(GUO Ye,WU Wenchuan,ZHANG Boming,et al.Power system state estimation solution with zero injection constraints using modified newton method and fast decoupled method in polar coordinate[J].Proceedings of the CSEE,2012,32(22):113-117.(in Chinese))
[ 9 ] GUO Ye,WU Wenchuan,ZHANG Boming,et al.An efficient state estimation algorithm considering zero constraints[J].IEEE Transactions on Power Systems,2013,28(3):2651-2659.
[10] WU F F,LIU W H,LUN S M.Observability analysis and bad data processing for state estimation with equality constraints[J].IEEE Transactions on Power Systems,1988,3(2):541-548.
[11] WU F F,LIU W H,HOLTEN L,et al.Observability analysisand bad data processing for state estimation usinghachtel's augmented matrix method[J].IEEE Transactions on Power Systems,1988,3(2):604-611.
[12] KORRES G N.A robust algorithm for power system state estimation with equality constraints[J].IEEE Transactions on Power Systems,2010,25(3):1531-1541.
[13] 颜全椿,卫志农,孙国强,等.基于主导与非主导参数的非线性加权最小绝对值参数估计[J].电力系统自动化,2013,37(20):71-76.(YAN Quanchun,WEI Zhinong,SUN Guoqiang,et al.A robust WLAV state estimation based on multiple predictor-corrector interior point method[J].Power System Technology,2013,37(20):71-76.(in Chinese))
[14] RAMIREZ J M,BAROCIO E E.Solving state estimation in power system by an interior pointmethod[J].International Journal of Electrical Power and Energy Systems,2000,22(5):355-365.
[15] WEI Hua,SASAK H,KUBOKAWA J,et al.An interior point method for power system weighted nonlinearL1norm static state estimation[J].IEEE Transactions on Power Systems,1998,13(2):617-623.
[16] 厉超,卫志农,倪明,等.基于变量代换内点法的加权最小绝对值抗差状态估计[J].电力系统自动化,2015,39(6):48-52,106.(LI Chao,WEI Zhinong,NI Ming,et al.WLAV robust state estimation based on variable substitution interior point method[J].Automation of Electric Power Systems,2015,39(6):48-52,106.(in Chinese))
PowersystemstateestimationusingbilinearWLAVmethodwithzeroinjectionconstraints
SHENTiantian1,HUANGQijian2,WUChangsheng2,SUNGuoqiang1,WEIZhinong1,ZANGHaixiang1
(1.CollegeofEnergyandElectricalEngineering,HohaiUniversity,Nanjing210098,China;2.ChizhouPowerSupplyCompany,Chizhou247000,China)
Power mismatches of zero injection nodes have significant impact on the security estimation of the power system. In this paper, a novel state estimation method for the power system is proposed to reduce the power mismatches of zero injection nodes, in which zero injection constraints are added in the form of equality constraints in the bilinear WLAV (Weighted Least Absolute Value). Based on the IEEE standard system, a case study on a provincial system is performed using this method. The results demonstrate that this method can not only ensure the existing high computational efficiency of bilinear WLAV based on interior point method, but also reduce the power mismatches of zero injection nodes. Meanwhile, its robustness is improved to a certain degree.
power system; state estimation; zero injection; equality constraints; interior point method; mismatch
10.3876/j.issn.1000-1980.2017.06.013
2016-11-21
国家自然科学基金(51277052,51507052)
沈甜甜(1993—),女,江苏宿迁人,硕士研究生,主要从事电力系统状态估计研究。E-mail:shentiantian99@163.com
卫志农,教授。E-mail:wzn_nj@263.net
TM744
A
1000-1980(2017)06-0556-06

