基于变论域模糊控制的无刷直流电机转速问题*

赵天宇, 苏庆宇

(东北电力大学 自动化工程学院,吉林 吉林 132012)

基于变论域模糊控制的无刷直流电机转速问题*

赵天宇, 苏庆宇

(东北电力大学 自动化工程学院,吉林 吉林 132012)

无刷直流电机(BLDCM)是一种多变量、强耦合、非线性、时变的复杂控制系统。由于其采用传统的PID控制时很难满足需要，所以针对BLDCM精确调速的控制问题，在基于传统PID控制上引入模糊控制设计了模糊PID控制，并在此基础上应用变论域的方法，设计了变论域模糊PID控制器。以BLDCM为模型，通过MATLAB建立其仿真模型。仿真和试验结果表明，采用变论域模糊PID控制的BLDCM与传统控制的BLDCM相比,具有响应速度快、超调小、控制精度高等优点。

无刷直流电机；调速控制；变论域模糊PID控制； MATLAB仿真

0 引 言

无刷直流电机(Brushless DC Motor,BLDCM)是伴随着微电子器件和电力电子器件的研究应运而生的，其原型是美国D. Harrison等人在1955年首次提出的可以代替机械电刷的晶体管换相电路。作为新一代机电一体化产品，它既具有直流电机响应速度快、起动转矩大的特点，又拥有异步电机运行可靠、结实耐用，制造、使用、维护方便等特点。这使得BLDCM在电力电子科技高速发展的今天能够应用于工业控制的各个领域[1-3]。我们国家对BLDCM的研究虽然才三十多年，但随着科技的日益发展，使得BLDCM在航空航天、医疗器械、家用电器、交通工具等诸多领域得到广泛应用，并在我国多地形成初具规模的产业链。随着机械加工技术的迅猛发展，BLDCM成本下降，现如今从电动遥控车到航天飞机BLDCM已经变得无处不在了。图1为我国自主生产的QT系列BLDCM。

图1 QT系列BLDCM

在BLDCM调速控制中，传统的PID控制虽然已得到较普遍的使用，但在参数时变、电动机负载大幅变化等方面受到很多非线性因素的影响，使得传统的PID控制手段难以达到设计初衷的理想状态。因此在传统的PID控制中加入智能控制算法已经成为当今一种比较热门先进的发展方向。

模糊控制极其适用在非线性、时变及纯滞后时间大、模型不完全系统的控制，并且有不要求控制对象精确数学模型、鲁棒性强、有较强容错能力等特点；PID控制适应性强，并且能够很好地消除系统的稳态误差。将这两种控制方法结合成模糊PID控制能使系统同时具备两种控制方法的优点[4-6]。但是，传统模糊控制器的结构随着控制规则的设计，确定了就不能再进行修改，使得其自适应能力受到很大限制，在消除系统稳态误差上的表现较差，当系统趋向于稳定时，易引起小范围振荡，难以得到很好的控制精度[7]。换句话说，传统模糊PID控制器尽管可以改善PID控制的缺点，但是又引发了不能有效改善系统控制性能的问题。因此，本文通过在控制器中加入变论域的思想，设计出变论域模糊PID控制器来对传统模糊PID控制器的不足进行改进；引入变论域环节可以使输入和输出基本论域随着控制需求自适应地发生伸缩变化，从而提高对BLDCM的控制精度。

1 BLDCM的变论域模糊PID控制器的设计

变论域模糊PID控制思想的关键，是找出PID的三个参数kp、ki、kd与转速误差e和转速误差变化率ec之间的模糊控制规则，通过模糊推理规则优化比例因子和量化因子参数，来满足不同误差e和误差的变化率ec对控制器参数的需求，从而使得PID控制器可以对BLDCM产生最优控制[8-10]。

1.1模糊PID控制系统设计

模糊PID控制器是在PID控制器基础上建立而成。本文采用离散型PID控制器，其数学表达式为

其中:ki=kpT/TI

kd=kpTD/T

式中:T——采样周期；

kp、ki、kd——三个可调节参数。

PID控制器的任务即决定这些参数的值。

模糊PID控制器是模糊PID控制的重要组成部分，多采用二维模糊PID控制器，其结构如图2所示。

传统村落最突出的社会问题来自老龄化与幼龄化，只有少部分的年轻人愿意留守村落。一方面，城市提供了大量的工作机会，相对较高的收入吸引他们外出务工；另一方面，传统的工作与务农成为年轻人眼中不入流、“没前途”的活计。

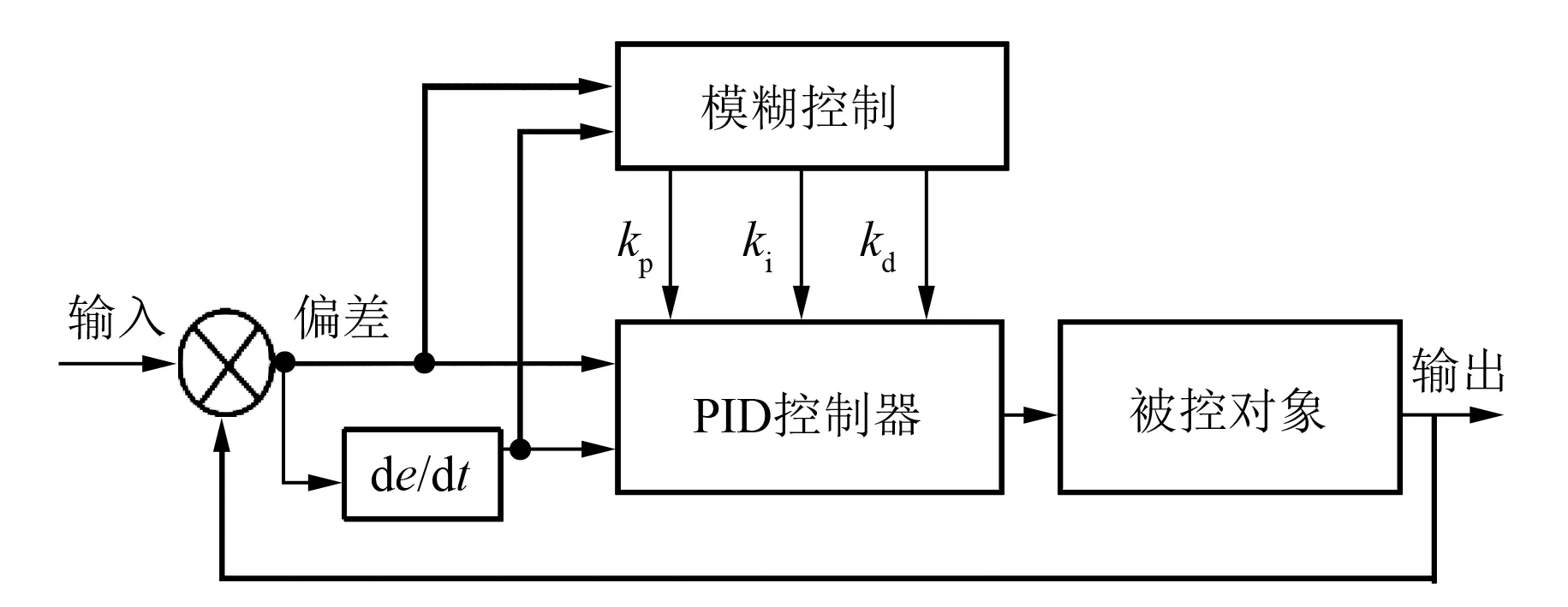
图2 模糊PID控制系统

模糊控制采用“Mamdani”模糊推理方法，系统首先检测出电机的实际转速n与给定转速n*，然后计算出转速误差e和误差的变化率ec。仿真中BLDCM转速变化范围为0～3 000 r/min，因此转速误差设定为-3 000～3 000 r/min，结合专家经验，设模糊PID控制器的输入变量误差e和误差变化率ec的论域E和EC均为{-7，-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6，7}，论域对应模糊子集为{NB，NM，NS，Z，PS，PM，PB}；模糊PID控制器的输出变量为kp、ki，论域均为{-7，-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6，7}，论域对应模糊子集为{NB，NM，NS，Z，PS，PM，PB}。转速误差e和误差的变化率ec与论域不同，设定比例因子使e和ec的变化在相同论域，其变换公式为

式中:X——实际输入的精确量，范围为[a,b]，将精确量X转化为模糊论域区间的量Y。

根据仿真中BLDCM的转速设置，确定模糊量为

通过式(3)、式(4)可以求出在同一论域下的模糊量e′、ec′。输出量kp、ki根据模糊规则求得的修正参数Δkp、Δki确定，公式为

式中:kp′、ki′——PID控制器的两个初始参数；

Δkp、Δki——模糊PID控制器的输出。

初始参数主要由传统的PID参数整定方法确定，通过上述式(5)、式(6)，可以得到模糊PID控制的比例、积分参数，并能进行实时整定。

(1)当偏差e和偏差变化率ec很大时，取较大的kp和较小的kd来使系统响应变快，为避免系统出现超调，取kd=0；(2)当偏差e和偏差变化率ec中等大小时，取较小的kp防止超调，较小的kd防止对系统影响过大；(3)当偏差e和偏差变化率ec很小时，为使系统具有较好的稳定性同时振荡较小，应取较大kp，取适当kd[10-12]。

模糊规则是模糊PID控制器的核心，通常根据操作者总结经验或者根据前人专家经验教训得到相应措施总结的一系列控制规则。响应曲线作为控制系统中决定控制品质的重要依据，也是制定模糊规则的首要标准。BLDCM响应曲线如图3所示。

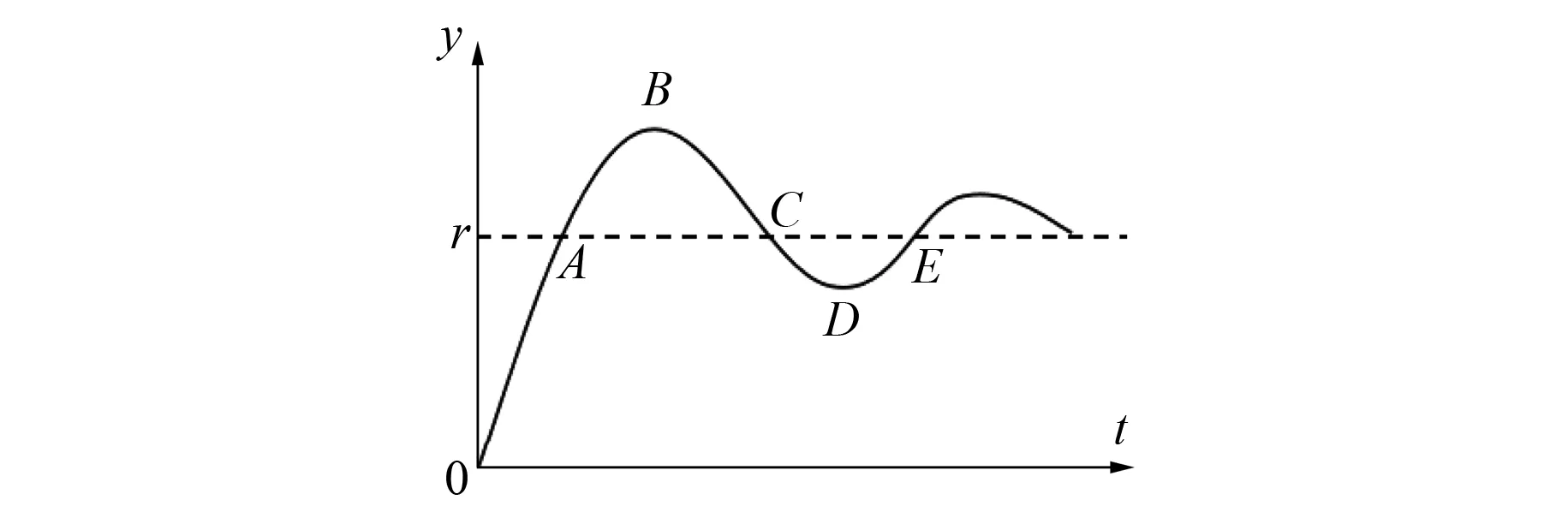
图3 BLDCM系统响应曲线

设y为电机实际转速，r为速度给定值。在0A阶段，ylt;r，转速偏差e=y-rlt;0，偏差为负，并且0A斜率大于0，所以偏差变化率ec大于0，为正；在AB段，ygt;r，转速偏差e=y-rgt;0，由于AB段斜率大于0，所以偏差变化率ec大于0；在BC段，ygt;r，转速偏差e=y-rgt;0，由于BC段斜率小于0，所以偏差变化率ec小于0；在CD段，转速偏差e=y-rlt;0，斜率与BC段一样小于0，所以偏差变化率ec小于0；在DE段，转速偏差e=y-rlt;0，由于DE段呈上升趋势，所以偏差变化率ec大于0。根据分析Δkp、Δki在不同阶段的模糊控制规则如表1、表2所示。

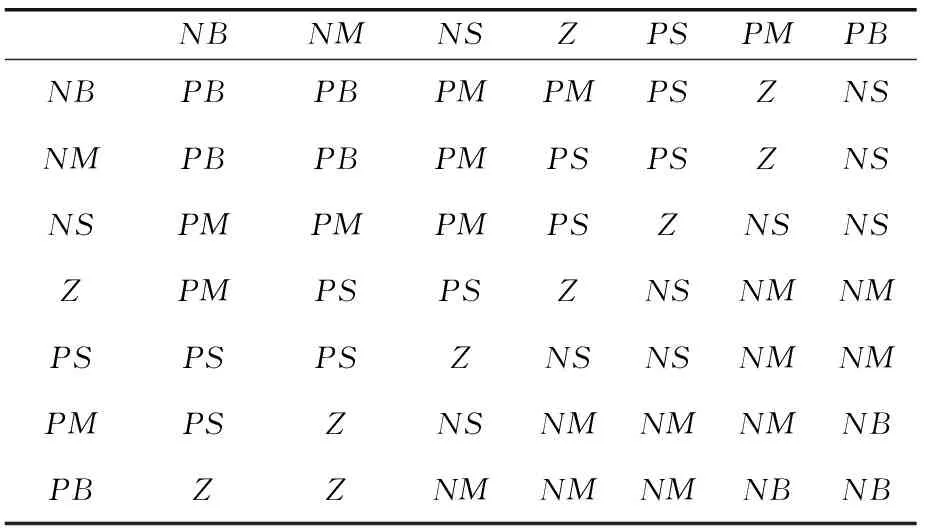
表1 Δkp模糊规则表

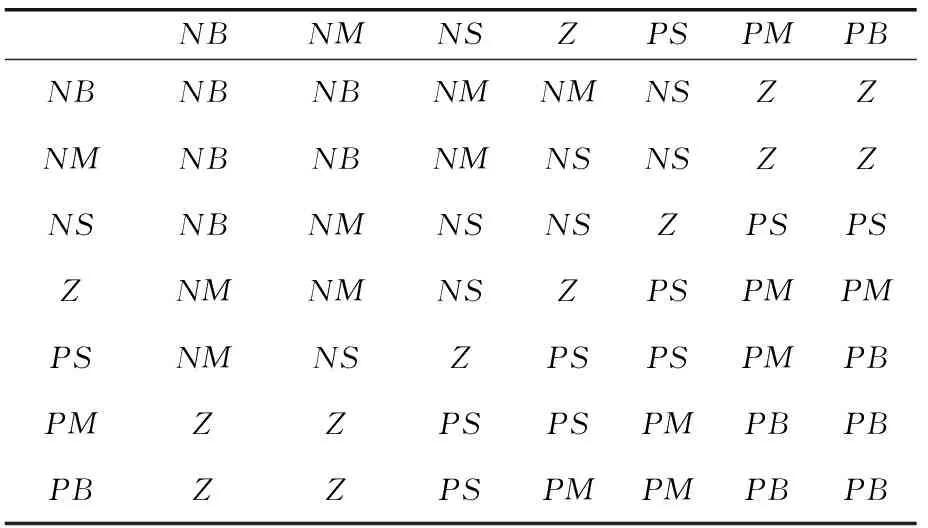
表2 Δki模糊规则表

1.2变论域模糊PID控制设计

基于变论域思想的模糊PID自适应控制器本质是利用伸缩因子改变输入输出论域，将变论域的思想加至模糊逻辑中，从而实现对PID参数的实时整定，定义在基本论域上的模糊划分会随输入和输出的基本论域按照控制需求的变化相应进行变化，提高系统的控制精度[13-14]。选取伸缩因子的方法有基于函数形式，也有基于模糊推理形式，本文选择基于模糊推理形式来描述模糊控制规则的伸缩因子。其基本思想如下：当输入变量变大，为了不影响系统上升且不增加超调，论域应维持不变；当输入变量变小，缩小论域，定义在论域上的模糊划分也会随之进行压缩，增加输入变量的可用规则。这平衡了模糊规则数量与控制精度的冲突，增加了控制灵敏度和稳态精度。设输入变量e和ec的伸缩因子分别为α1和α2，表3为基于模糊规则的输入论域伸缩因子规则。其中B、M、S、Z为论域“扩张或缩小的程度”。

表3 输入论域伸缩因子规则

对于输出论域伸缩因子β的取值，应通过e和ec来选取，即根据e和ec当前取值所反映的系统响应状态来判断输出论域该进行多大程度的扩张或者缩小。当e和ec很大，并且两者符号相同，说明系统与设定值之间存在很大的差距，且系统正以很快的速度偏离设定值，将使误差扩大得更剧烈，这时需要较大的控制量将系统尽快调回设定值[15-18]。因此参数应取大些以使输出论域扩大。表4为基于模糊规则的输出论域伸缩因子规则。

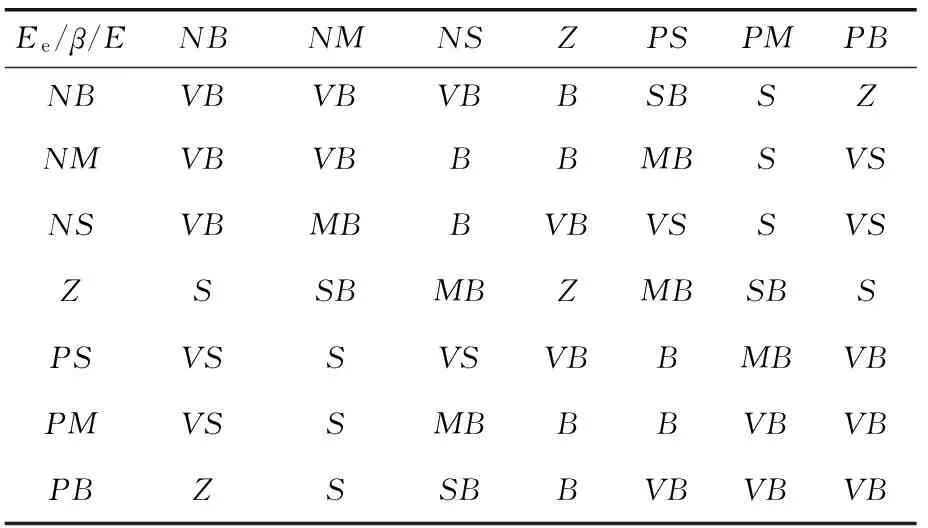
表4 输出论域伸缩因子规则

2 变论域模糊PID控制的BLDCM的MATLAB/Simulink仿真

BLDCM系统建模主要包括电机本体建模、功率驱动部分建模及控制系统建模。现如今，主要有两种方式对BLDCM进行建模：第一种是将其简化为直流电机利用传递函数进行建模仿真；第二种是利用MATLAB软件提供的(PowerSystemBlock,PSB)工具箱对BLDCM进行建模。仿真分析两种建模方式，前一种利用传递函数建模方式虽有搭建方法简单、仿真速度快的特点，但是忽略了电机续流、换相等信息；后一种建模方式与电机实际运行相仿，但搭建方法复杂，仿真速度慢[19-21]。为了反映电机运行的真实状态，便于仿真与试验结果的对照，本文采用了第二种建模方式对电机系统进行分析。为验证模型的准确性，将对仿真模型进行仿真。其SIMULINK如图4所示。变论域模糊PID控制器模块仿真模型如图5所示。

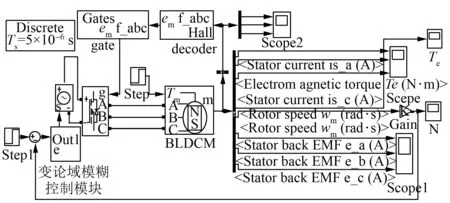
图4 变论域模糊控制的BLDCM

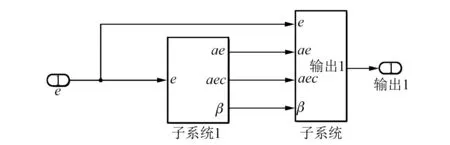
图5 变论域模糊PID控制器模块

BLDCM设置参数如下：励磁脉冲宽度120°，转动惯量J=0.000 8kg·m2，极对数p=4，阻尼系数B=0.001 4N·m·s/rad，定子相绕组电阻R=2.875Ω，定子相绕组电感L=0.008 5H。PID参数：kp=0.136，ki=163.800 2，kd=0。以上述参数的BLDCM做被控对象，在相同条件下，采用本文所述的变论域模糊PID控制、模糊PID控制及PID控制对被控对象转速进行以下几种情况的比较。

2.1电机正转仿真分析

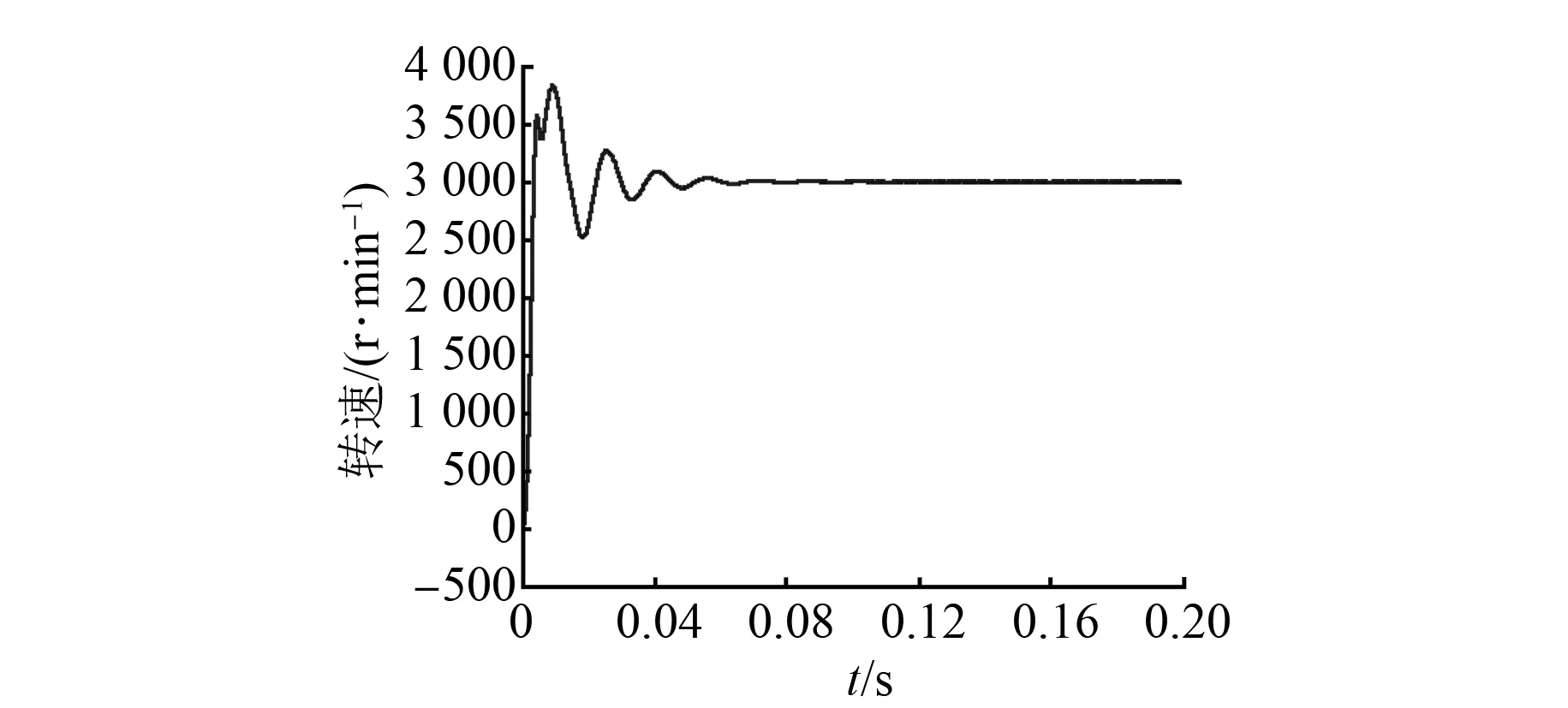
图6 基于PID控制的电机转速

设置电机转速为3 000r/min，可通过图6和图7仿真曲线得出，模糊PID控制和PID控制都能快速达到给定转速，但也都存在超调，模糊PID控制超调量要比PID控制小，并且没有像PID控制一样发生剧烈振荡；可以从图7和图8即变论域模糊PID控制与模糊PID控制对比发现，他们两个都更快速地达到给定转速，变论域模糊PID控制超调量稍小一点，在趋于稳定时变论域模糊PID控制振荡小于模糊PID控制。

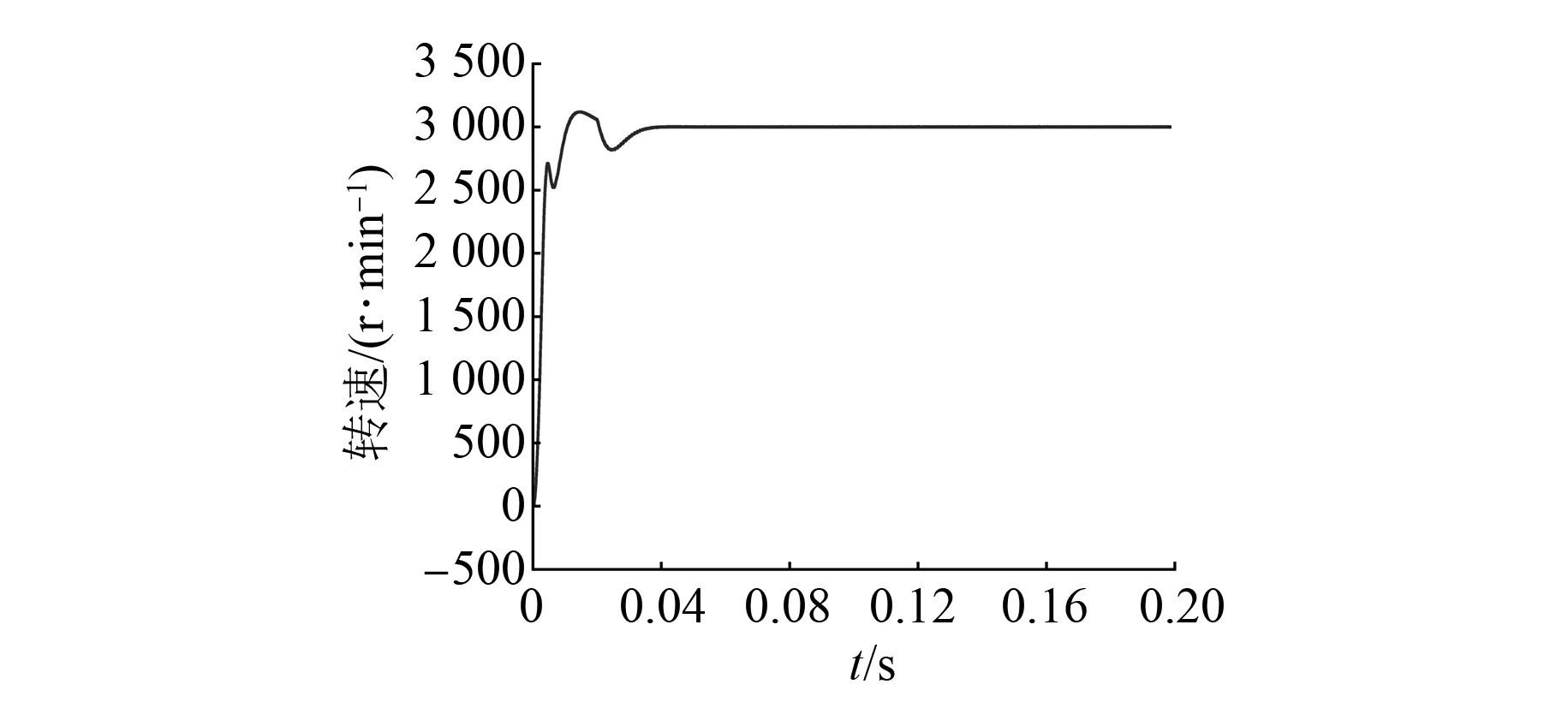
图7 基于模糊PID控制的电机转速

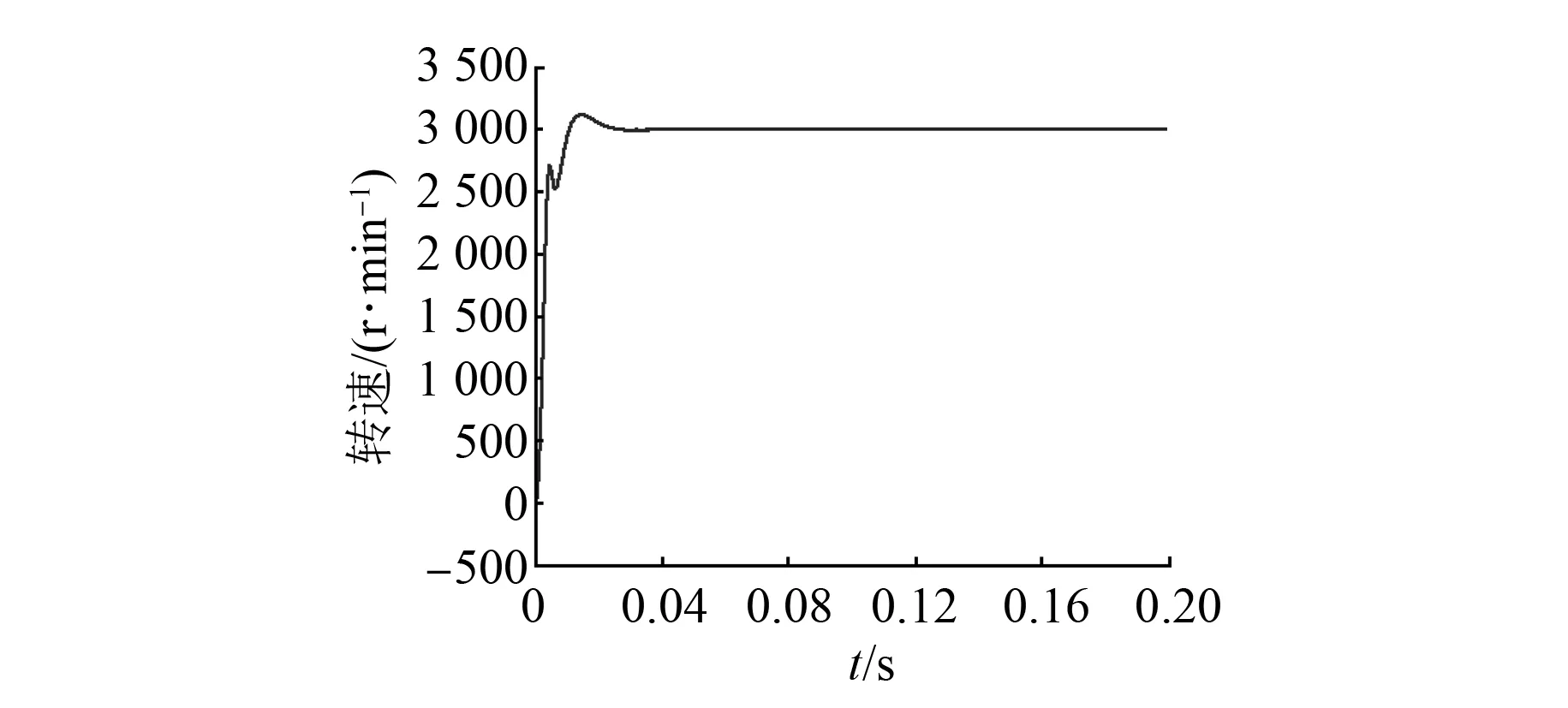
图8 基于变论域模糊PID控制的电机转速

2.2抗干扰能力的仿真分析

设置电机转速为3 000r/min，电机运行在0.1s时负载突然改变，对系统抗干扰能力的仿真结果如图9、图10所示。从图9和图10仿真曲线可看出，PID控制在加入负载时振荡更厉害，回复速度稍慢一些，变论域模糊PID控制回复速度快，对系统影响更小。所以从仿真结果看，变论域模糊PID控制抗干扰能力更强。

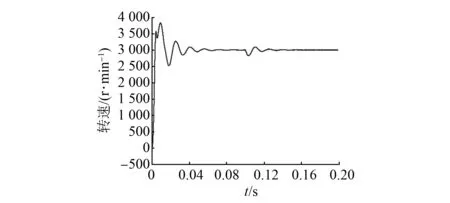
图9 基于PID控制的电机转速

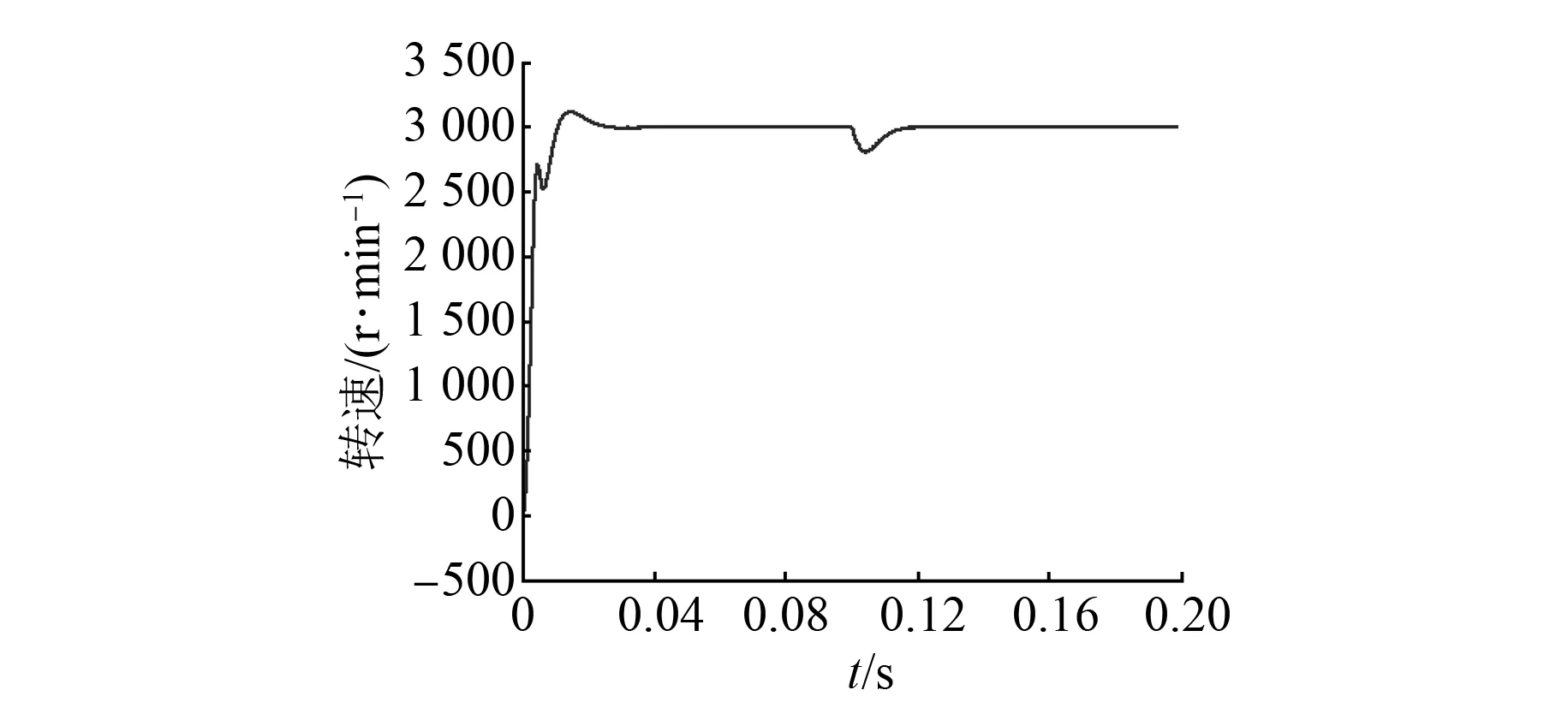
图10 基于变论域模糊PID控制的电机转速

图11 基于PID控制的电机转速

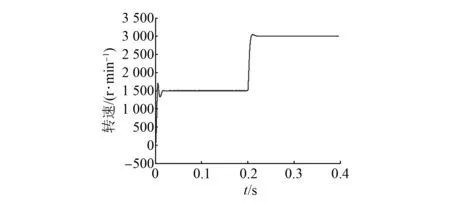
图12 基于变论域模糊PID控制的电机转速

2.3转速变化的仿真分析

设置电机转速为1 500r/min，当趋于稳定后，电机转速设置为3 000r/min，从图11和图12仿真曲线看出，变论域模糊PID控制在跳变过程中要比PID控制超调量小，并且更加平稳。

3 结 语

本文采用的是变论域模糊PID控制对BLDCM转速调节进行控制。变论域模糊PID控制基本操作方法是通过在模糊PID控制的输入输出变量上加入伸缩因子使变论域模糊PID控制得以实现。在BLDCM调速方面，比较中可以发现，变论域模糊PID控制的自适应能力和抗干扰能力以及克服振荡的能力都要优于模糊PID控制和PID控制。这体现了这种变论域模糊PID控制的有效性，为以后分析这类问题和对应的控制策略研发打下了一个好的基础；并且，变论域模糊PID控制器实现简单，计算量少，适应性好，可以作用在高动静态性能及高控制精度的调速及数字伺服控制系统。本文尚可完善之处是对比例因子量化因子取值不够精确，希望在日后的仿真中加以改进，使BLDCM转速调节控制更加精准。

[1] 夏长亮.无刷直流电机控制系统[M].北京:科学出版社,2009.

[2]CHENGKY,TZOUYY.DesignofasensorlesscommutationICforBLDCmotors[J].IEEETransactionsonPowerElectronic(S0885-8993),2013,18(6): 1365-1375.

[3] 夏长亮,方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3): 25-34.

[4] 温嘉斌,麻宸伟.无刷直流电机模糊PI控制系统设计[J].电机与控制学报,2016,20(3): 102-108.

[5] 史冬琳,李芸芸,张博超.基于模糊PID控制器的磨煤机控制系统设计[J].东北电力大学学报(自然科学版),2009,29(2): 20-23.

[6] 王葳,张永科,刘鹏鹏.无刷直流电机模糊PID控制系统研究与仿真[J].计算机仿真,2014,29(4): 196-199.

[7] 李洪兴.变论域自适应模糊控制器[J].中国科学E辑,1999,29(1): 33-42.

[8] 李洪兴.非线性系统的变论域稳定自适应模糊控制器[J].中国科学E辑,2004,32(2): 211-223.

[9] 龙祖强.变论域模糊控制器的若干重要问题研究[D].长沙:中南大学,2011.

[10]LIYES,JISHENP.Thestudyoffuzzy-PIcontrolerofpermanentmagnetsynchronousmotor[J].IEEEIntertationalPower,2009(5): 32-34.

[11] 陈伟,周小波,王群京.基于模糊优化的PID直流无刷电机控制[J].电子设计工程,2010,18(6): 146-149.

[12] 李军伟,崔师,李连强,等.基于模糊PID的无刷直流电机控制系统设计开发[J].机械设计与制造,2013(2): 77-79.

[13] 窦艳艳,钱蕾,冯金龙.基于Matlab的模糊PID控制系统设计及仿真[J].电子科技,2015(2): 119-122.

[14]HUJQ,LITS,GUOC.DesignofGA-basedfuzzycontrolforshipsteering[J].TheSixthWorldCongresson,2006(1): 3594-3598.

[15] 杨贞富.基于MatlabSimulink的变论域模糊控制算法仿真方法[J].科技展望,2016,25(12): 155.

[16] 谭兵文,李春文.几种变论域伸缩因子选择方法的比较研究[J].科学技术与工程,2013,13(2): 909-911.

[17]JIANY,LUOJ,CHENZP.Variableuniverseadaptivefuzzycontrolforliquidlevel[C]∥ 2008InternationalSymposiumonComputationalIntelligenceandDesign,IEEE,2008: 158-161.

[18] 王华强,过一涵.温室温度变论域Mamdani控制器的设计[J].化工自动化及仪表,2016,43(1): 12-15.

[19] 刘海珊,陈宇晨.无刷直流电机PID控制系统仿真及实验研究[J].系统仿真学报,2009,21(8): 157-160.

[20] 刘慧博,王静,吴彦合.无刷直流电机模糊自适应PID控制研究与仿真[J].控制工程,2014,21(7): 583-587.

[21] 凡庆,许渝峰,闫宽宽.无刷直流电机双闭环控制的仿真研究[J].汽车实用技术,2016(3): 16-19.

BrushlessDCMotorSpeedQuestionsBasedonVariableUniverseFuzzyControl*

ZHAOTianyu,SUQingyu

(School of Automation Engineering, Northeast Electric Power University, Jilin 132012, China)

Brushless DC motor (BLDCM) was a multivariable, strong coupling, nonlinear, time-varying complex control system, the use of traditional PID control was difficult to meet the needs, so in the BLDCM control precision speed control problems, Based on the traditional PID control fuzzy control design fuzzy PID control, and on the basis of the variable domain method used to design a variable universe fuzzy PID controller. Then, using BLDCM as model, the simulation model was established by MATLAB. Simulation and experimental results showed that the BLDCM with variable universe fuzzy control had the advantages of faster response speed, smaller overshoot and higher control precision compared with the traditional BLDCM.

brushlessDCmotor(BLDCM);speedcontrol;variableuniversefuzzyPIDcontrol;MATLABsimulation

国家自然科学基金资助项目(61403075，61503071)

赵天宇(1992—)，男，硕士研究生，研究方向为智能控制在无刷直流电机上的应用。苏庆宇(1982—)，男，博士，副教授，研究方向为故障检测、非线性控制等方面的教学与科研。

TM 615

A

1673-6540(2017)11- 0006- 06

2017 -03 -06