基于果蝇-蛙跳模糊神经网络PID 的永磁直线同步电机控制

乔维德

(无锡开放大学，江苏 无锡 214011)

基于果蝇-蛙跳模糊神经网络PID的永磁直线同步电机控制

乔维德

(无锡开放大学，江苏 无锡 214011)

针对永磁直线同步电机(PMLSM)伺服系统存在的非线性、时变性及强耦合性，设计一种基于模糊神经网络PID的速度控制策略，通过融合果蝇优化算法和蛙跳算法形成果蝇-蛙跳算法，实时调整优化模糊神经网络的结构参数，输出适用于PID控制器的最佳参数kp、ki、kd，实现PMLSM速度控制的自适应和智能化。仿真分析与试验结果表明，采用基于果蝇-蛙跳算法优化的模糊神经网络PID速度控制器，能使PMLSM控制系统取得更加优良的控制效果。

永磁直线同步电机；模糊神经网络；果蝇-蛙跳算法； PID控制

0 引 言

相对于旋转电机而言，由永磁直线同步电机(Permanent Magnet Linear Synchronous Motor，PMLSM)组成的直线伺服系统，因为省略了从旋转电机至工作台之间的所有机械传动环节，能够直接将电能转化为直线运动机械能，并不需要任何中间转换机构，具有结构简单、高速度、高精度、高耐久性、直接驱动等优点，目前已在机器人、高精度数控机床、半导体制造等工业控制领域得到广泛应用。但是，在PMLSM直接驱动系统中，直线同步电机和工作台之间缺少了中间的缓冲机构和环节，使得系统参数变化、负载干扰、推力波动、摩擦力等不确定因素直接作用并影响PMLSM，加大了PMLSM系统控制难度[1]，再加之直线电机系统属于多变量、参数时变、强耦合性的非线性系统，从而大大影响了直线同步电机控制系统的控制性能。为此，需要采取有效的控制方案，尤其对PMLSM控制系统的控制器进行重新设计，以削弱甚至消除系统参数摄动、外界扰动等因素对系统控制性能的影响。

以往PMLSM调速系统中的速度控制器采用传统PID控制方法，尽管PID算法简单，且有一定的控制精度，但仍为线性控制，远不能满足PMLSM非线性系统高精度、快响应的要求。因此，很多学者提出PID控制与人工智能相结合的技术方案，设计了模糊PID控制器、模糊神经网络(Fuzzy Neual Network,FNN)PID控制器等。从已有研究文献分析，FNN PID控制器中用于优化FNN的学习算法主要采取BP算法、遗传算法等，但在学习训练中存在学习过程长、易于早熟等问题。因此，本文设计FNN PID控制器作为PMLSM控制系统的速度控制器，且将果蝇优化算法(Fruit Fly Optimization Algorithm，FOA)、蛙跳算法(Frog Leaping Algorithm，FLA)相融合生成一种新型的果蝇-蛙跳混合算法(FOA-FLA)，利用该算法在线优化FNN结构参数并输出PID最优参数，从而更好地满足PMLSM伺服控制系统的性能要求。仿真分析与试验结果表明，PMLSM系统采取FNN PID速度控制策略，系统响应快、无超调、控制精度高、鲁棒性及抗扰动能力强，从而能更加精准地实现PMLSM速度控制。

1 PMLSM的数学模型

PMLSM应用矢量控制策略，采用坐标变换方法，建立d、q坐标轴模型下的数学模型[2]。

PMLSM的电压和磁链方程表达式为

PMLSM的电磁推力表达式为

PMLSM的机械运动方程表示为

式中：ud、uq——d、q轴电压；

id、iq——d、q轴电流；

Ld、Lq——d、q轴电感；

ψd、ψq——d、q轴的绕组磁链；

ψf——定子永磁体磁链；

RS——绕组电阻；

τ——电机极距；

Fe——直线电机的电磁推力；

FL——直线电机的负载阻力；

B——粘滞摩擦因数；

v——直线电机的机械运动速度；

M——直线电机的质量。

PMLSM具有参数时变性、非线性、强耦合性、受负载扰动影响大等特点和问题，如果仍采用传统的线性控制方法(如PID控制)，则会极大地影响对PMLSM系统的控制效果。

2 PMLSM控制系统结构

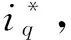
3 FNN PID控制器

基于FNN PID控制器的PMLSM控制系统，将PMLSM的速度差值e及其变化率ec=de/dt作为模FNN的输入量，FNN输出PID控制器运算所需的最优参数kp、ki、kd，PID控制器采用增量式PID运算，其输出u(k)算式为

图1 PMLSM控制系统结构原理图

FNN结构如图2所示。网络由输入层(i层)、隶属函数层(j层)、规则层(k层)、输出层(O层)组成[3]。

图2 FNN结构示意图

(2) 第2层为隶属函数层或模糊化层。该层主要用来计算各输入量的隶属度值，对其进行模糊化处理。每个输入量都各自用模糊子集{ND、NM、NX、ZE、PX、PM、PD}来表示，其中，ND、PD分别代表为负大、正大，NM、PM分别代表负中、正中，NX、PX分别代表负小、正小，ZE为零。该层的输出为各节点输入变量对应模糊子集的隶属度函数，这里采取高斯型函数作为隶属度函数。该层共有14个节点，第j个节点的输出与输入的关系为

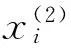
(3) 第3层为模糊规则层。该层通过与上一层隶属函数层的连接，实现模糊规则的合理匹配及其神经元各节点之间的模糊推理运算。根据PMLSM系统特点及其对速度控制的要求，PID控制器的参数kp与输入量e、ec之间的模糊规则如表1所示，ki、kd与e、ec之间的模糊规则与表1类似(此处略)。

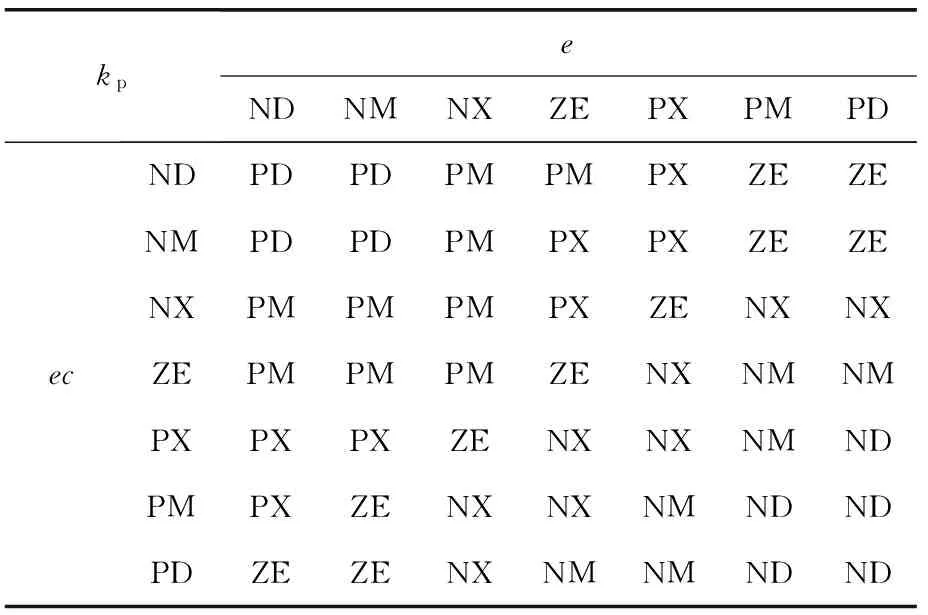
表1 kp与e、ec间的模糊规则

该层中每个节点神经元均对应1条模糊逻辑运算规则。从表1可以生成kp的模糊推理规则49条，所以kp、ki、kd共有对应模糊规则147条，即模糊规则层共含有147个神经元。该层输出可表示为

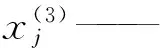
ωjk——隶属函数与规则层之间的连接权值。

(4) 第4层为输出层。该层共有3个节点，输出量为规则层输出信号经处理后的总和。

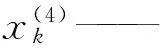
ωko——第3层与第4层间的连接权值；

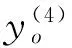
在以上FNN结构模型中，第2层的14个节点中高斯函数的均值mij和标准差δij以及第3、4层间的连接权值ωko均需要调整和优化。

4 FNN的学习算法及其训练

可调参数mij、δij、ωjk、ωko对FNN PID速度控制器的控制性能有着重要影响，FNN通过对结构参数的不断学习和训练，从而取得本系统期望控制效果的PID控制器参数kp、ki及kd。笔者应用FOA-FLA训练优化FNN结构参数，以增强速度控制器的控制性能和鲁棒性。

4.1FOA

FOA是由台湾中国科技大学潘文超博士于2011年新提出的一种群体智能优化算法。该算法充分利用果蝇敏锐的嗅觉和视觉功能，通过模仿果蝇觅食行为及其特性，实现全局寻优。FOA的主要优化过程为

第1步： 参数初始化。初始化果蝇群体规模groupsize，最大迭代次数maxnum，随机设定果蝇群体初始位置即X_axis、Y_axis。

第2步： 种群初始化。随机设置果蝇个体利用嗅觉搜索食物目标的方向及距离，随机数rand设为果蝇优化迭代步进值。

第3步： 种群评价。因为不能确定食物的具体位置，所以首先估算果蝇与原点之间的距离di，然后测算果蝇个体的味道浓度判定值Si,接着将味道浓度判定值Si代入味道浓度判别函数(也称为适应度函数Fitness Function)，计算果蝇个体位置的味道浓度tastei，并从群体中寻找味道浓度最佳的果蝇个体。

第4步： 选择操作。记录且保留最高味道浓度值besttaste及其对应X、Y坐标轴值，同时果蝇凭借敏锐的视觉飞向该坐标值位置，形成新的果蝇群聚位置。

第5步： 果蝇迭代寻优。重复按第2步、第3步进行迭代寻优，及时判断当前果蝇最佳味道浓度是否优于前次迭代味道浓度，若是则执行第4步。如果当前味道浓度不再优于以往迭代的味道浓度，或者迭代次数已满足最大迭代次数maxnum，则果蝇算法结束。

4.2FLA

FLA是在2003年由Eusuff等学者提出的一种模拟青蛙群体觅食行为的智能优化方法。对于D维搜索空间，N只青蛙构成初始种群，第i只青蛙设为Xi=(Xi1，Xi2，Xi3，…，XiD)，i=1，2，…，N。将青蛙各个体按照适应度值从高到低排列，且分成m个族群(子群)，每个族群(子群)又都有k只青蛙，即N=m×k。在每个族群(子群)中，适应度最好的解用Xb表示，适应度最差的解用Xw表示，全部族群中适应度最好的解用Xg表示。在FLA进化进程中，需要对族群(子群)中适应度最差(青蛙)的解Xw进行更新计算。

式中:R——[0，1]区间上的随机数；

Dj——在第j维上移动距离；

Dmax——青蛙位置一次更新改变的最大值。

如果Xw(new)的适应值比原来解Xw适应值差，则用整个蛙群最优个体Xg替换式中Xb；然后按式(11)、式(12)执行更新操作。如果得到的Xw(new)适应值依然没有变好，则随机产生一新解(青蛙)替换原来的解Xw(即最差青蛙)。此更新操作不断重复进行，直至达到蛙跳算法设定的迭代次数maxnuml为止。

4.3FOA-FLA

FOA的全局搜索能力强、收敛速度快，但是该算法在反复迭代寻优进程中，向最优果蝇个体的聚集行为，极大影响种群多样性，也极易导致算法陷入局部最优，出现收敛早熟现象。FLA具有较强的局部深度搜寻能力。为充分发挥FOA和FLA各自优势，并弥补其不足，本文将FOA和FLA进行有机融合，形成FOA-FLA。FOA-FLA不仅保持FOA全局搜索寻优较强和收敛速度较快等性能，而且又具备FLA较好的局部深度搜索能力，从而有效克服FOA极易陷入局部最优的问题与缺陷[4]。FOA-FLA的运行流程如图3所示。

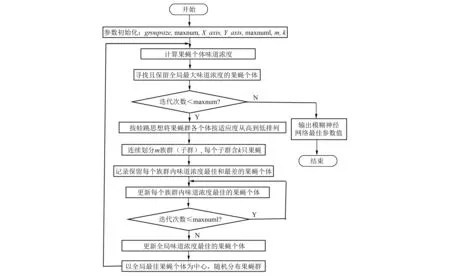
图3 FOA-FLA运行流程图

4.4FNN的训练

将FNN结构参数mij、δij、ωjk、ωko置于一多维向量，每一个参数均看作FOA-FLA中的果蝇个体。初始化种群时随机产生N只果蝇，每只果蝇构成一个FNN，通过输入样本对这些FNN进行训练。每个FNN在训练样本集中的均方误差(即目标函数)为

式中:n——样本个数；

Yk,p——训练样本p在第k个输出节点的实际输出；

Qk,p——对应的期望输出。

设定Fitness=1/(MSE+1)作为测算FOA-FLA的适应度函数，用来对每个果蝇个体进行适应度评价，直至搜寻到果蝇群体中的最佳个体。当MSE小于给定误差或者FOA-FLA的进化迭代次数超过最大进化迭代次数时，则FOA-FLA训练FNN过程结束。

5 仿真分析与试验验证

5.1系统仿真

采用软件工具MATLAB/Simulink搭建PMLSM控制系统的仿真模型[5]。仿真用PMLSM参数设置如下：电枢绕组电阻RS=3.25 Ω，电感Ld=Lq=32.75 mH，动子质量M=5.5 kg，极距τ=36 mm，粘滞摩擦因数B=6 N·s/m，永磁体磁链ψf=0.28 Wb，FL=200 N。FOA-FLA参数选取如下：果蝇种群规模groupsize=200，最大混合迭代次数maxnum=500，果蝇优化迭代步进值rand在[-1，1]内取值；FLA的最大内迭代次数maxnuml=15，族群(子群)数m=20，每个族群(子群)内的个体个数k=10，随机初始化果蝇群体位置(X_axis，Y_axis)为待优化FNN结构参数的搜索空间。在PMLSM电流、速度双闭环控制系统中，电流内环仍使用传统的PID控制器，而速度外环由本文设计的FNN PID控制器作为速度控制器。

为了进行对比研究，本文先后采取传统PID控制器、BP算法优化的FNN PID控制器(BP-FNNPID)、遗传算法优化的FNN PID控制器(GA-FNNPID)、经FOA-FLA优化的FNN PID控制器(FOA-FLA-FNNPID),分别取代PMLSM控制系统中的速度控制器，图4为PMLSM的输出响应比较曲线，其中设定的给定速度为vr=5 mm/s的阶跃信号，曲线①、②、③、④分别表示传统PID、BP-FNNPID、GA-FNNPID、FOA-FLA-FNNPID 4种不同速度控制器条件下的响应曲线。由图4比较分析，经FOA-FLA优化的模糊神经网络PID控制器用于速度控制器时，PMLSM控制系统的稳态误差最小，系统调整时间最短，系统跟踪响应速度也最快，具体性能对比情况列于表2。当系统在t=0.21 s时突减50 N负载时，FOA-FLA优化的FNN PID控制器系统受到外界负载变化扰动的影响最小，系统的鲁棒性能最强。

图4 不同控制器作用下PMLSM系统响应曲线

5.2试验验证

为了进一步验证FOA-FLA优化FNN PID控制器的控制性能及其控制效果，建立PMLSM控制试验平台，试验原理示意图如图5所示。试验控制芯片使用DSP芯片TMS320F2812，DSP完成PMLSM控制系统的数据采集、信号处理与控制等功能。系统控制的外围电路包括功率驱动器、逆变器电路、电流采样检测电路、示波器、PC机、CAN通信电路等。给定PMLSM的速度为6 mm/s阶跃信号，且在t=0.17 s时突加10 N·m负载，采取本文设计的FOA-FLA优化FNN PID速度控制器时的速度响应曲线如图6所示。从图6可以明显观察出系统调整时间较短，超调量非常小，几乎为零，并且t=0.17 s时因负载干扰而引起的速度变化量仅为-0.04 mm/s，试验取得了与上面仿真相类似的结果。试验结果进一步表明，经FOA-FLA优化的FNN PID控制器能使PMLSM控制系统的响应速度加快、稳态精度提高、抗扰动能力以及鲁棒性能增强。

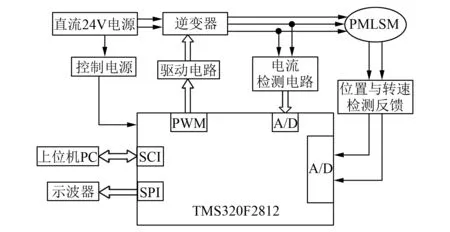
图5 验证FOA-FLA-FNNPID性能的试验原理图

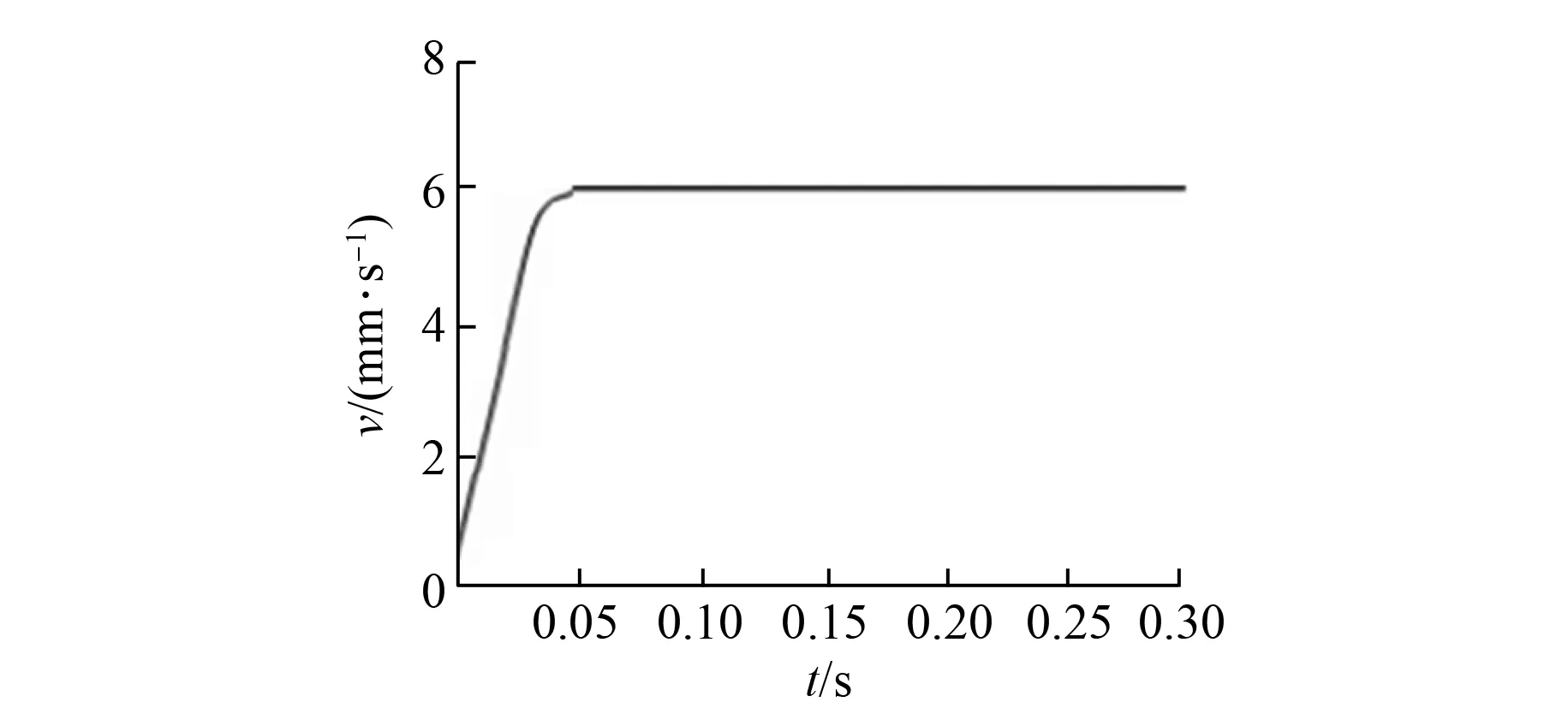
图6 基于FOA-FLA-FNNPID控制的速度响应

6 结 语

针对PMLSM伺服系统中的非线性、不确定性，且在电机运行中极易受负载扰动影响等问题，本文将传统PID控制与FNN控制有机结合起来，设计一种FNN PID控制器作为PMLSM控制系统的速度控制器，并且将FOA和FLA两种群体智能算法融合形成FOA-FLA，以FOA-FLA在线优化FNN的结构参数，输出PID控制器最优参数kp、ki、kd，从而提高PMLSM控制系统的动、静态性能。仿真与试验取得良好的优化效果，对于PMLSM的工程应用有一定的指导意义。

[1] 胡江.永磁同步直线电机智能化PID速度控制研究[J].信息技术,2015(8): 96-99.

[2] 武琳,王丽梅,左涛.基于神经网络的永磁直线同步电机位置控制[J].电气技术,2009(3): 17-20.

[3] 乔维德.遗传算法优化的开关磁阻电动机RFNN位置控制器设计[J].微特电机,2016,44(2): 75-77.

[4] 刘成忠,黄高宝,张仁陟,等.局部深度搜索的混合果蝇优化算法[J].计算机应用,2014,34(4): 1060-1064.

[5] 党明辉,郭亮.基于模糊神经网络PID的永磁同步直线电机控制算法研究[J].浙江理工大学学报(自然科学版),2016,35(1): 52-57.

PermanentMagnetLinearSynchronousMotorPIDControlBasedonFruitFlyOptimizationAlgorithm-FrogLeapingAlgorithmandFuzzyNeuralNetwork

QIAOWeide

(Wuxi Open University, Wuxi 214011, China)

According to the nonlinear, time-varying and strong coupling of the servo system of permanent magnet linear synchronous motor (PMLSM), a speed control strategy based on fuzzy neural network PID was designed, through fruit fly optimization algorithm (FOA) and frog leaping algorithm (FLA) made fruit fly optimization algorithm-frog leaping algorithm (FOA-FLA), it real time adjust and optimized the structure parameters of fuzzy neural network, the output were suitable for PID controller of the best parameterskp、ki、kd, it had realized adaptive and intelligent control for PMLSM speed control. Simulation analysis and experimental results showed that, Using the PID speed controller of fuzzy neural network based on FOA-FLA, the permanent magnet linear synchronous motor control system could get better control effect.

permanentmagnetlinearsynchronousmotor(PMLSM);fuzzyneuralnetwork;fruitflyoptimizationalgorithm-frogleapingalgorithm(FOA-FLA);PIDcontrol

乔维德(1967—)，男，教授，研究方向为电机智能控制、机电设备故障智能诊断等。

TM 301.2

A

1673-6540(2017)11- 0055- 06

2016 -12 -19