永磁直线同步电机伺服系统鲁棒反步控制器设计*

陈志翔, 高钦和, 谭立龙, 牛海龙

(火箭军工程大学 二系,陕西 西安 710025)

永磁直线同步电机伺服系统鲁棒反步控制器设计*

陈志翔, 高钦和, 谭立龙, 牛海龙

(火箭军工程大学 二系,陕西 西安 710025)

针对永磁直线同步电机(PMLSM)伺服系统强鲁棒性、高控制精度的要求，提出一种鲁棒反步控制器。为了解决常规PID跟踪精度不高、参数调节难度大及鲁棒性差的问题，将自适应控制与反步控制结合。利用自适应机制实时估计系统的扰动，去除了反步控制设计过程中对外界扰动上界的要求，同时克服了控制律高频抖振的问题。同时，分析了闭环反馈系统中高频噪声的特性以及对系统的不利影响，使用低通滤波器来抑制高频噪声。最后，在Googol公司的试验平台上，通过与一种改进的PID对比,验证了设计的鲁棒反步控制器的可行性以及抑制高频噪声的有效性,可为先进控制理论的工程化提供参考。

永磁直线同步电机伺服系统；自适应控制；反步；高频噪声

0 引 言

直线电机伺服系统具有高动态响应和高控制精度的特点，广泛应用于各种工业领域[1]。相比于传统的“旋转电机+丝杠”的机械结构，直线电机的电磁推力可直接作用于负载上，而不需要中间的传动装置。因此，直线电机伺服系统没有齿侧间隙、摩擦力较大等缺点，系统具有更高的推力密度、更快的动态响应、更低的热量耗散和更简单的机械结构。但是，其特殊的机械结构，直线电机伺服系统的性能更容易受系统不确定因素的影响，如由电机自身结构引起的推力波动，包括齿槽力和端部效应，由导轨产生的非线性摩擦力，系统参数的不确定性和摄动，由负载变化引起的扰动，由机械系统的死区柔性等引入的非线性环节等。这使得高性能直线电机的控制系统设计变得更加复杂。传统永磁直线同步电机(Permanent Magnet Linear Synchronous Motor,PMLSM)伺服系统多采用PID控制算法，但是PID算法不仅参数调节难度较大，而且对负载变化的适应能力不强，需要根据系统面临的不同情况来调节PID参数。

近年来，以Kokotovic及其合作者发展起来的反步法引起了有关学者的高度关注[2]。这种设计方法通过逐步修正算法设计镇定控制器实现系统的全局调节与跟踪，在每一步把状态坐标的变化、不确定参数的调节函数和一个已知的Lyapunov函数的虚拟系统的镇定函数联系起来，适用于可状态线性化的参数不确定系统。I. Kanellakopoulos等[3]首次将反步法应用于电机的控制器设计中。近年来，文献[4-8]也研究了反步法在电机控制系统中的应用。

本文将自适应算法和反步法结合，设计了针对PMLSM伺服系统的鲁棒反步控制器，并利用Lyapunov稳定性理论给出了闭环控制系统的稳定性证明。在Googol公司的直线电机伺服试验平台上，首先将本文设计的鲁棒反步控制器与改进的不完全微分PID控制算法对比，验证了设计的控制算法的可行性;其次，通过对比控制系统中有无低通滤波器，验证闭环控制系统中抑制高频噪声的必要性。

1 系统建模

针对一种U型槽直线电机进行建模(如图1所示)。该类型直线电机适用于高速、高加速、高精度运动系统，无齿槽力，运动平滑性好。但是该类型直线电机存在由边缘效应引起的推力波动。负载是由滚珠导轨支撑，摩擦力可能随着接触面变化而变化，因此摩擦力呈现较明显的与位置相关的非线性。本文将推力波动和摩擦力均视为干扰。

图1 U型槽直线电机伺服系统

该系统模型表达式为

式中:x、v——位移和速度；

M——动子和负载的总质量；

Fm——电机推力；

Df、Dr、Du——摩擦力、推力波动和其他干扰。

由于电流环的动态响应速度远大于机械响应速度，因此可以将电流环假设为理想的比例环节，则有：

其中：K=Ka·Km

式中:u——控制输入；

K——推力常数；

Ka——驱动器常数；

Km——推力因数。

为了更精确地描述非线性摩擦力，采用修正的“Coulomb+粘滞”模型来表示：

式中:Dc(x)、Dv(x)——随位置变化的Coulomb摩擦因数和粘滞摩擦因数。

推力波动是位移的函数，与电机是否通电无关，采用正弦函数及其高次谐波将其模型表示为

式中:Dai——幅值；

τ——电机的极距；

φi——相位。

Du代表直线电机运行过程中的其他干扰，如标称系统与实际系统的误差，外界推力的干扰等。

2 鲁棒反步控制器设计

系统模型表达式(1)可表示为

式中:z1——直线电机的位移跟踪误差，z1=x-x*。

V1(z1)的导数为

定义稳定函数α1和速度跟踪误差z2为

设计式(8)中的稳定函数α1为

式中:k1——大于0的正常数。

将式(9)、式(8)代入式(7)有

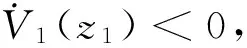
V2(z1,z2)的导数为

设计控制律u为

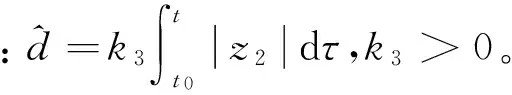
构造Lyapunov函数：

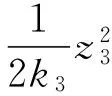
V3(z1,z2,z3)的导数为

设计的自适应反步控制律为

将式(15)和式(18)代入式(17)，得

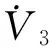
根据LaSalle不变原理[9]，设计的自适应反步控制器可实现系统渐进稳定。

3 高频噪声的特性分析与抑制

第二部分设计的自适应反步控制器需要在每个控制周期中获取直线电机的状态量：位移和速度。将式(18)展开：

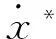
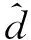
设系统的真实状态量(位移x1和速度x2)由执行机构反馈至控制器的过程中引入外界高频的噪声Δx1、Δx2，则参与控制器解算的状态量为

根据连续时间系统频率响应理论[10]，由式(22)可得关于高频噪声Δx1和Δx2之间关系的推论。

推论一：位移信号x1和速度信号x2引入的高频噪声Δx1和Δx2频谱分布相同，但是Δx2相对于Δx1，相位超前π/2，同一频率信号的幅值比为频率的大小，Δx2的幅值更大。

此时，控制器解算的控制律与理论值存在偏差：

由式(23)可得关于控制律偏差的推论。

推论二：由于实际应用中状态反馈环节存在不可避免的高频噪声Δx1和Δx2，导致控制器解算的实际控制律偏离理论值。控制律的偏离值Δu是由Δx1和Δx2各自放大一定倍数后叠加而成，因此实际控制律亦含有与Δx1和Δx2相同频谱的高频分量。

由推论二可知，若不对状态反馈环节的高频噪声进行抑制，则会导致驱动器输送至直线电机的电流变大，造成电能的浪费，还会使直线电机推力不稳定，直线电机运行的噪声大。

4 试 验

用如图1所示的直线电机控制系统开展试验。该直线电机系统的负载为总质量1.4 kg的砝码，直线电机动子的质量为1.79 kg，粘滞摩擦因数经试验测得为Dv(x)=0.1 N/(m/s)，驱动器常数Ka=0.84 A/V，推力系数为Km=15 N/A。首先，通过与一种改进的不完全微分PID控制对比，验证自适应反步控制器的可行性。然后，对比有无低通滤波器两种情况下自适应反步控制器的控制效果，验证在闭环反馈中抑制高频噪声的必要性。

4.1自适应反步控制器可行性验证

期望信号为y=0.1 sin(t)，设置施加弹簧拉力作为外界干扰力，如图2所示。不完全微分PID的传递函数为

式中:kp、TI、TD——比例、积分、微分系数；

τ——滤波器系数。

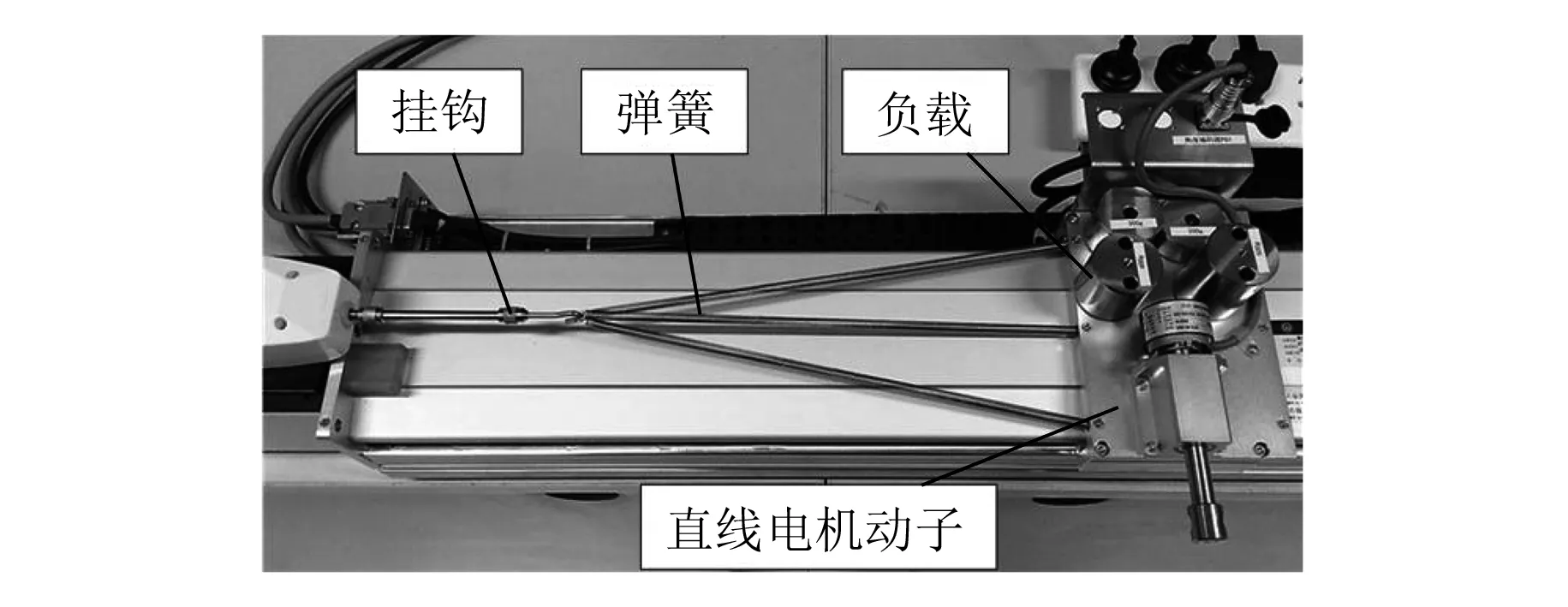
图2 设置外界干扰力的试验装置

试验结果如图3、图4所示。

从图3位移跟踪曲线看，不完全微分PID与自适应反步控制器都可以较好地跟踪期望的正弦信号。从位移跟踪误差曲线看，自适应反步控制器跟踪误差的幅值明显小于不完全微分PID。

图3 位移跟踪试验结果

为了更精确地描述跟踪效果，定义均方根误差(Root Mean Square Error，RMSE)：

自适应反步控制器的RMSE=4.2×10-4，不完全微分PID的RMSE=1.6×10-3，自适应反步控制器的跟踪精度相对于不完全微分PID提高了74%。因此，自适应反步控制器的跟踪效果优于不完全微分PID。

图4反映的是有无弹簧拉力情况下对干扰的观测值。可以看到，有弹簧拉力相对于无弹簧拉力的情况，干扰观测值出现了明显的偏移，该偏移量的变化趋势与实际情况下弹簧的拉力变化趋势相同。这表明，自适应算法可以实时估计系统的干扰，提高系统的鲁棒性。

图4 干扰观测值试验结果

4.2抑制高频噪声必要性验证

设置闭环状态反馈通路有无低通滤波器两种情况，对比自适应反步控制器的控制效果。试验过程中，声音强度(Sound Pressure Level，SPL)的定义为

其中:P0=2×10-5Pa。

试验结果如图5～图8所示。

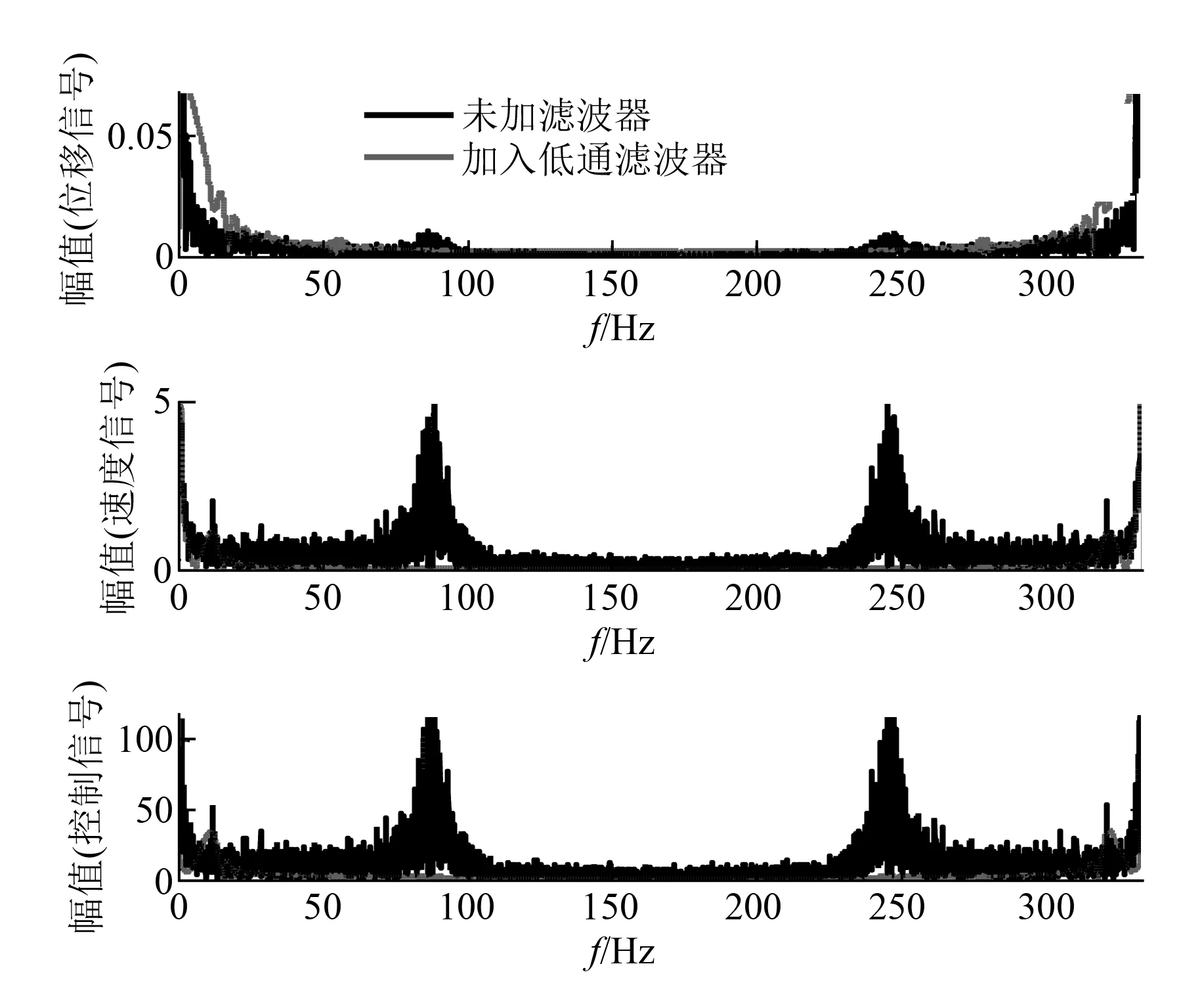
图5 对位移、速度和控制信号的傅里叶变换

在图5中，对于未加入滤波器的情况，位移信号和速度信号中高频噪声的频谱分布相同，高频噪声频率主要分布在70～100 Hz，而且速度信号中高频噪声的幅值远大于位移信号中高频噪声的幅值，验证了推论一。由于位移信号和速度信号中高频噪声的引入，导致控制信号中也存在高频噪声，并且此高频噪声的频谱分布与位移和速度信号相同，验证了推论二。由于加入了低通滤波器，滤出了位移信号和速度信号中的高频噪声，同时控制信号中也没有了高频噪声，信号的能量主要集中在低频段，高频段各个信号的幅值很小。

在图6中，未加入低通滤波器的位移跟踪误差幅值(3×10-3)约为加入滤波器情况(5×10-4)的6倍，相位相差了π，从而导致未加入低通滤波器的控制律信号幅值(2 V)约为加入低通滤波器的控制律信号幅值(0.3 V)的6倍，相位也相差了π。为了提高控制系统的鲁棒性，式(20)的控制律系数的选择满足：k1·k2≫k1+k2，此时速度跟踪误差对控制信号幅值影响较小。

图6 位移误差试验结果

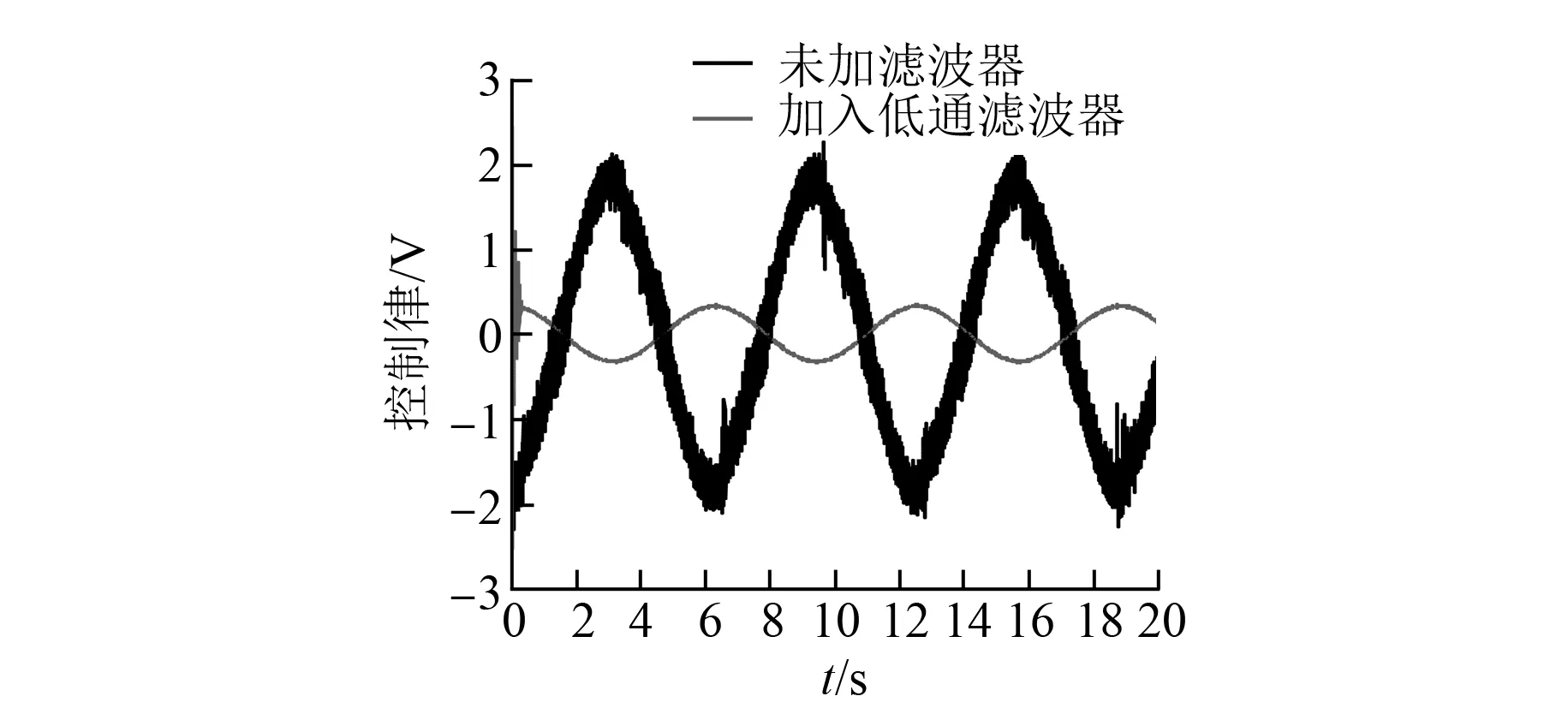
图7 两种情况下的控制律

根据推论一，由于速度信号中高频噪声的幅值远大于位移信号中高频噪声的幅值，从图7的时域信号以及图5的频域信号可以看到，速度信号的高频噪声会导致控制信号中含有高频噪声，这将导致直线电机推力波动严重，系统运行噪声较大。在图8中，未加入滤波器的情况下，系统运行的声音强度在85 dB波动，而加入滤波器之后，系统运行的声音强度降至60 dB。

图8 对两种情况下机器运行噪声的测量结果

综合上述试验结果可以看到，状态反馈环节的高频噪声不仅会导致驱动器输送至直线电机的电流变大，造成电能的浪费，还会使直线电机推力不稳定，直线电机运行的噪声大，从而验证了抑制高频噪声的必要性。

5 结 语

本文对一种U型槽直线电机伺服系统进行建模，对系统的机械子系统设计了一种鲁棒反步控制器。同时从工程的角度，分析了闭环反馈系统中高频噪声的特性、影响及抑制的必要性。通过在Googol公司的直线电机伺服平台上进行试验，验证了设计的控制器的可行性以及抑制高频噪声的必要性。

[1] 叶云岳.直线电机原理与应用[M].北京:机械工业出版社,2000.

[2] KOKOTOVIC P V. The joy of feedback: nonlinear and adaptive[J].IEEE Control Systems,1992,12(3): 7-17.

[3] KANELLAKOPOULOS I, KREIN P T, DISILVESTRO F. Nonlinear flux observer-based control of induction motors[C]∥ Proc ACC’92，1992: 1700-1705.

[4] TING C S, LIEU J F, LIU C S, et al. An adaptive FNN control design of PMLSM in stationary reference frame[J]. Journal of Control, Automation and Electrical Systems,2016,27(4): 391-405.

[5] LINARES F J, GARCA R C, SIRA R H, et al. Robust backstepping tracking controller for low-speed PMSM positioning system: design, analysis, and implementation[J]. IEEE Transactions on Industrial Informatics,2015,11(5): 1130-1141.

[6] CHEN M Y, LU J S. Application of adaptive variable speed back-stepping sliding mode controller for PMLSM position control[J].Journal of Marine Science and Technology,2014,22(3): 392-403.

[7] TING C, CHANG Y, SHI B, et al. Adaptive backstepping control for permanent magnet linear synchronous motor servo drive[J].Iet Electric Power Applications,2015,9(3): 265-279.

[8] 付培华,陈振,丛炳龙,等.基于反步自适应滑模控制的永磁同步电机位置伺服系统[J].电工技术学报,2013,28(9): 288-293.

[9] KRSTIC M, KOKOTOVIC P V, KANELLAKOPOULOS I. Nonlinear and adaptive control design[M].New York: A Wiley-Interscience Publication,1995.

[10] 潘仲明.信号、系统与控制基础教程[M].北京:高等教育出版社,2012.

DesignofRobustBacksteppingControllerforPermenentMagnetLinearSynchronousMotorServoSystems*

CHENZhixiang,GAOQinhe,TANLilong,NIUHailong

(The 2nd Department, Rocket Force University of Engineering, Xi’an 710025, China)

A robust backstepping controller for permanent magnet linear synchronous motor (PMLSM) servo systems to meet the requirements of strong robust and high precision was presented. To solve the problems of low-accuracy, difficult parameters tuning and weak robust, an adaptive controller and a backstepping one were combined. The introduction of adaptive mechanism released the priori knowledge of upper bounds on disturbance and overcomed the chattering problem of the control law. Meanwhile, the characteristics and the bad impacts of high-frequency noise in feedback control systems were analyzed, and a low pass filter was applied to suppress the high-frequency noise. Finally, the effectiveness of the proposed controller and the suppression of the high-frequency noise were verified in the experimental platform, made by Googol company. This paper could provide references to the practicality of advanced control theory.

permanentmagnetlinearsynchronousmotor(PMLSM)servosystems;adaptivecontrol;backstepping;high-frequencynoise

国家自然科学基金项目(51475462)

陈志翔(1991—)，男，博士研究生，研究方向为永磁直线同步电机控制与应用。

TM 351

A

1673-6540(2017)11- 0032- 06

2017 -03 -06