组合体航天器有限时间超螺旋反步姿态控制

马广富，高 寒，吕跃勇，宋 婷，袁建平

(1. 哈尔滨工业大学控制科学与工程系, 哈尔滨 150001；2. 上海航天控制技术研究所, 上海 200233；3. 西北工业大学航天学院, 西安 710072)

组合体航天器有限时间超螺旋反步姿态控制

马广富1，高 寒1，吕跃勇1，宋 婷2，袁建平3

(1. 哈尔滨工业大学控制科学与工程系, 哈尔滨 150001；2. 上海航天控制技术研究所, 上海 200233；3. 西北工业大学航天学院, 西安 710072)

针对服务航天器与非合作空间目标构成的组合体航天器的姿态控制问题，提出一种基于干扰观测器的有限时间控制策略。首先，设计一种改进的超螺旋干扰观测器对由非合作目标导致的较大转动惯量不确定性及外界干扰进行观测，并分析了观测误差的有限时间收敛特性；然后，结合反步法设计了有限时间姿态控制器，同时引入指令滤波器提高了反步法的控制性能；最后，通过数值仿真校验了所提算法的有效性。

组合体航天器；超螺旋干扰观测器；有限时间；反步姿态控制；指令滤波器

0 引 言

近年来，以在轨维护、在轨加注及空间碎片清除等为代表的在轨服务技术已成为航天领域广泛关注的焦点，被认为是未来航天技术的主要发展方向[1]。服务航天器(亦称主动航天器)与目标航天器完成抓捕对接后构成的组合体的姿态控制问题是在轨服务的关键技术之一[2]。由于目标航天器尤其是非合作目标的质量、结构特性往往是未知的，因此新的组合航天器存在较大的转动惯量不确定性、未建模动态以及外部干扰等，为其高精度姿态控制提出了挑战[3]。

对于航天器存在转动惯量不确定性及外界干扰，现有的处理方法一般有两种：自适应控制或观测器方法。宋斌等[4]研究了航天器姿态机动过程中的鲁棒自适应控制；Tiwari等[5]研究了将自适应与二阶积分滑模相结合的刚体航天器的姿态控制问题；Huang等[6]则针对目标捕获后的绳系组合航天器研究了自适应反步控制。以上文献中均采用自适应技术处理了系统不确定性并取得了良好的控制效果，但只是对系统不确定性的上界进行估计以增加系统鲁棒性，而不能对系统的时变不确定性进行实时观测。相比之下，设计合理的观测器能够实现对时变不确定性的实时在线估计，在航天器控制等领域得到了广泛应用。文献[7]利用非线性干扰观测器(Nonlinear disturbance observer，NDO)处理了航天器大角度姿态机动过程中的不确定性；Liu等[8]利用NDO对挠性航天器的弹性振动进行观测。(上述经典NDO均需要对干扰的变化率作出限制，一般假设干扰为常值或慢变信号，同时存在观测器收敛速度慢以及观测精度低的问题)。针对NDO的不足，Xiao等[9]将滑模观测器引入到航天器姿态容错控制中，Xia等[10]利用扩张状态观测器技术处理航天器姿态控制中的不确定性。以上提到的观测器虽然相比于NDO有了一定的改进，但是存在自身的一些问题，例如滑模观测由于符号函数的存在，不可避免地会在观测过程中引入抖振现象，同时上述观测器均不能保证观测误差有限时间收敛，与近年来受到广泛关注的有限时间观测器相比其观测性能有待进一步提高。超螺旋滑模具有有限时间收敛特性并且克服了传统滑模的抖振问题[11]，在控制器和观测器的设计中都得到了广泛应用。Davila等[12]利用超螺旋设计了速度观测器，虽然能够保证有限时间，但是其观测器增益是固定的，动态特性有待提高。Shtessel等[13]介绍了一类自适应增益的超螺旋控制器，控制器的增益项不再是常值，可以实时调整。

为了确保整个控制系统的有限时间特性，需要在有限时间干扰观测器的基础上设计有限时间姿态控制器，保证系统的全局有限时间，由于反步法具有鲁棒性较高的优点，有文献将反步法与有限时间方法相结合，提出有限时间反步控制。Guo等[14]设计了航天器姿态有限时间反步控制器，Liu等[15]基于反步技术设计了航天器姿态鲁棒控制器，但上述文献均采用一般形式的反步设计方法。近些年来，有学者提出基于指令滤波器技术的反步设计方法[16]，该方法可以解决反步设计过程中微分计算复杂的缺点，同时对信号的幅值、带宽及变化率进行限制，被广泛研究。文献[17]将指令滤波器技术应用于高超声速飞行器的控制中，Hu等[18]则采用基于指令滤波器的自适应反步方法对垂直起降飞行器进行控制，宋申民等[19]利用指令滤波器处理控制受限的航天器轨道跟踪问题，虽然相关的指令滤波器方法已经被应用到飞行控制系统的设计中，但是上述方法只适用于特定的被控制对象且对系统的有限时间收敛特性考虑较少。

本文针对组合体航天器存在的较大转动惯量不确定以及外部干扰，设计了一种基于超螺旋干扰观测器(Super-twisting disturbance observer,STDO)的航天器有限时间姿态控制策略，提出了有限时间稳定的观测器和控制器；改进了超螺旋算法的自适应项，使其具有更好的动态特性；引入了指令滤波器，改善了基于反步法的有限时间控制器性能。

1 数学建模与基本概念

(1)

(2)

(3)

(4)

非合作目标的转动惯量无法获知，可视为组合体航天器存在的转动惯量不确定性，表示成如下形式：

J=J0+ΔJ

(5)

式中：J0表示航天器转动惯量的标称值即主动航天器转动惯量，ΔJ表示附加转动惯量。

为便于控制器设计，现令x1=qv，x2=ω,并将式(5)代入式(3)后对与ΔJ有关的不确定项进行分离处理,可转化成如下标准形式

(6)

针对式(6)所描述的组合体航天器，本文控制目标为设计相应的有限时间观测器及有限时间控制器，使得系统状态x1及x2在有限时间内收敛到包含原点的邻域内。下面给出有限时间稳定的概念及常用引理。

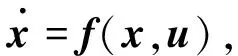
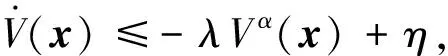
2 自适应超螺旋干扰观测器设计

(7)

定义系统状态x2的估计误差以及广义干扰D的观测误差分别为

(8)

(9)

参照文献[11]中标准超螺旋算法的一般形式，设计广义干扰观测器如下所示

(10)

结合式(6)和式(7)，可得

(11)

显然，若x2的观测误差e是有限时间收敛的，则广义干扰观测误差也是有限时间收敛的。如式(10)所示，标准超螺旋算法的观测器增益为固定值而无法根据干扰的变化实时调整。对此，本文设计了观测器增益能够根据干扰而实时自适应调整的新型自适应超螺旋干扰观测器。

定理1. 对于组合体航天器系统(6)，当广义干扰D满足假设1时，设计自适应超螺旋干扰观测器为

(12)

其自适应项为

(13)

式中：a，b，τ，χ以及ψm为正常数。如果存在正常数ρ和λ，使得

(14)

成立，则系统状态误差和广义干扰观测误差是实际有限时间稳定的。

证. 为方便证明，首先选取中间变量M∈R3×1，N∈R3×1且有

(15)

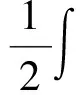
(16)

结合式(11)和式(12)对式(15)、(16)求导,可得

(17)

(18)

(19)

(20)

选取Lyapunov函数

(21)

(22)

(23)

而针对式(21)，有下式成立

(24)

可进一步得到

(25)

通过式(23)和式(25)可以得到

(26)

进一步选取另一个Lyapunov函数

(27)

式(27)可以转化为如下所示

(28)

(29)

对式(29)进一步整理后可得

(30)

式中：κ=min(μ,l1a,l2a)。

(31)

当ψigt;ψm时，将式(13)代入式(31),可得

(32)

当ψi≤ψm时，将式(13)代入式(31),可得

(33)

注1. 相比于经典的固定增益的超螺旋干扰观测器，本文提出的自适应超螺旋增益可随着系统误差而变化，且与文献[22]相比，本文的自适应超螺旋增益ψi不会一直增大而是在系统进入稳态后保持在ψm的邻域内，因此系统不会因增益过大而失稳。

注2. 相比于文献[13]中的自适应算法，本文算法用a(|ei|-χ)代替了asgn(|ei|-χ)，使得自适应增益的幅值可以随着系统误差进行动态调整并最终稳定在一个特定值附近，有效避免了符号函数导致的剧烈切换，从而令动态过程更加平稳。

3 基于指令滤波的有限时间反步控制

反步法基于迭代的设计思想，通过设计合理的虚拟控制量使得每步迭代都是Lyapunov稳定的。然而反步法在每步设计过程中均需要进行微分计算，在实际任务中微分信号比较难以获取，因此有学者提出在反步法中采用指令滤波器计算微分信号，图1为指令滤波器的示意图。

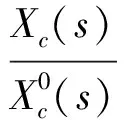
(34)

基于指令滤波器的反步有限时间控制器设计步骤如下：

1)定义经过补偿后的误差信号

(35)

(36)

2)定义补偿更新律并设计虚拟控制量

(37)

(38)

式中:α1,i为虚拟控制量;c1，c2以及γ均为正常数。

3)设计实际控制量

(39)

(40)

为了处理广义干扰对系统的影响，将第2节所设计的干扰观测器(12)代入式(39)，可得

(41)

结合步骤1)～3)，可以得到定理2的具体内容如下：

定理2. 考虑由式(6)描述的航天器，应用自适应超螺旋干扰观测器(12)对航天器的广义干扰进行观测，同时采用控制器(39)进行姿态控制时，v1,i将在有限时间T1内收敛到0，v2,i将在有限时间T2内收敛到|v2,i|≤Δ。其中,T1≤max{t0,t1,t2,t3,t4}，T2≤max{t1,t2,t3,t4}。

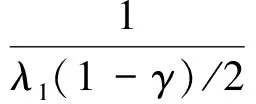
(42)

(43)

(44)

证. 针对v1,i选取Lyapunov函数为

(45)

并对式(45)求导,可得

v1,i(-c1v1,i-c2sigγ(v1,i))≤

(46)

此时式(46)符合引理2的要求，令λ1=2c1，λ2=2(γ+1)/2c2，v1,i将在有限时间t0收敛到零。

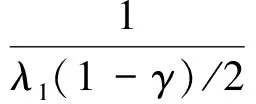
(47)

进一步，选择一个新的Lyapunov函数

(48)

对式(48)求导，并代入控制器(39),可得

(49)

(50)

其中，σ为任意正常数。

将式(50)代入式(49)并进行整理,可得

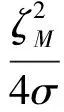
(51)

对式(51)整理可得

(52)

(53)

(54)

整理式(51),可得

(55)

(56)

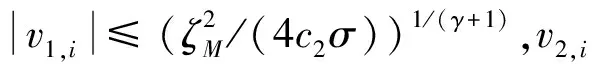
(57)

对式(51)整理可得

(58)

(59)

(60)

对式(51)整理可得

(61)

(62)

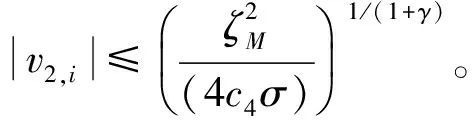
(63)

因此，通过以上分析，v1,i将在有限时间T1内收敛到0，v2,i将在有限时间T2内收敛到|v2,i|≤Δ。

4 仿真分析

本文通过数值仿真对设计的干扰观测器和控制器进行了仿真校验。本文所设计的基于自适应超螺旋干扰观测器的有限时间指令滤波控制器(STDOFTCF，式(41))分别与反步控制器(BS，文献[23])，有限时间指令滤波控制器(FTCF，式(39))在相同的初始条件下进行了对比。

控制器参数选为c1=0.5，c2=0.45，c3=0.5，c4=0.45，γ=0.85。

图2和图3分别给出了航天器的姿态以及角速度的响应曲线，本文所提算法姿态误差在20 s内达到了1×10-3数量级。虽然其他两种算法也能达到预期的姿态稳定目标，但其他两种算法所需的控制力矩更大，并且收敛速度均要小于本文所提算法的收敛速度。与此同时，30 s～50 s期间的稳态误差表明本文所提算法具有更高的控制精度。

三种算法所需的控制力矩如图4所示，通过观察可以看出本文所提算法在初始阶段所需的控制力矩要小于其他两种算法，同时在30～50 s的稳态过程中，所需控制力矩与其他两种算法处于同一数量级上且相差不大，并没有因为控制精度的提高而需要更大控制输出。

图5为干扰估计值与外界干扰的对比图，图中ED表示外界干扰，DE表示广义干扰估计值。从图5可以看出，干扰观测器很好地跟踪了干扰的变化。图6给出了超螺旋干扰观测器中自适应项的变化情况，可以看到自适应增益自动地根据所跟踪干扰的情况进行调整，使得其能够更好地对广义干扰进行估计；同时稳定在切换值附近，也与上文的分析结果保持一致。上述仿真对比表明，本文所提的算法具有良好的控制性能，为解决相关在轨服务组合体航天器的姿态控制问题提供了一个值得参考的解决思路。

5 结 论

本文提出了一种基于超螺旋干扰观测器的组合体航天器有限时间姿态控制方案。在该控制方案中，改进的自适应增益超螺旋干扰观测器被用于估计由组合体航天器的转动惯量不确定性以及外界扰动所组成的广义干扰。利用观测值，设计了有限时间反步控制器并引入指令滤波器，在完成有限时间控制的同时，提高了反步法的控制品质。通过Lyapunov稳定性分析方法，证明了存在转动惯量不确定性以及外界扰动的情况下整个控制系统的有限时间收敛特性。数值仿真结果证明了本文所提算法的有效性与正确性。

[1] Flores-Abad A, Ma O, Pham K, et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in Aerospace Sciences, 2014, 68: 1-26.

[2] 梁斌, 徐文福, 李成, 等. 地球静止轨道在轨服务技术研究现状与发展趋势[J]. 宇航学报, 2010, 31(1): 1-13.[Liang Bin, Xu Wen-fu, Li Cheng, et al. The research status and development trend of the GEO on-orbit servicing technology[J]. Journal of Astronautics, 2010, 31(1): 1-13.]

[3] 刘厚德, 梁斌, 李成, 等. 航天器抓捕后复合体系统稳定的协调控制研究[J]. 宇航学报, 2012, 33(7): 920-929.[Liu Hou-de, Liang Bin, Li Cheng, et al. Research on coordinate control method for stabilizing a coupling system after the spacecraft is captured[J]. Journal of Astronautics, 2012, 33(7): 920-929.]

[4] 宋斌, 李传江, 马广富, 等. 航天器姿态机动的鲁棒自适应控制器设计[J]. 宇航学报, 2008, 29(1): 121-125.[Song Bin, Li Chuan-jiang, Ma Guang-fu, et al. Robust adaptive control of spacecraft attitude[J]. Journal of Astronautics, 2008, 29(1): 121-125.]

[5] Tiwari P M, Janardhanan S, Nabi M U. Rigid spacecraft attitude control using adaptive integral second order sliding mode[J]. Aerospace Science and Technology, 2015, 42: 50-57.

[6] Huang P, Wang D, Meng Z, et al. Adaptive postcapture backstepping control for tumbling tethered space robot-target combination[J]. Journal of Guidance, Control, and Dynamics, 2015, 39(1): 150-156.

[7] 张银辉, 杨华波, 江振宇, 等. 基于干扰估计的航天器大角度姿态机动鲁棒次优控制[J]. 宇航学报, 2015, 36(10): 1148-1154.[Zhang Yin-hui, Yang Hua-bo, Jiang Zhen-yu, et al. Spacecraft large angle attitude maneuver robust suboptimal control based on disturbance estimation[J]. Journal of Astronautics, 2015, 36(10): 1148-1154.]

[8] Liu H, Guo L, Zhang Y. An anti-disturbance PD control scheme for attitude control and stabilization of flexible spacecrafts[J]. Nonlinear Dynamics, 2012, 67(3): 2081-2088.

[9] Xiao B, Hu Q, Singhose W, et al. Reaction wheel fault compensation and disturbance rejection for spacecraft attitude tracking[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(6): 1565-1575.

[10] Xia Y, Zhu Z, Fu M, et al. Attitude tracking of rigid spacecraft with bounded disturbances[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 647-659.

[11] Moreno J A, Osorio M. Strict Lyapunov functions for the super-twisting algorithm[J]. IEEE Transactions on Automatic Control, 2012, 57(4): 1035-1040.

[12] Davila J, Fridman L, Levant A. Second-order sliding-mode observer for mechanical systems[J]. IEEE Transactions on Automatic Control, 2005, 50(11): 1785-1789.

[13] Shtessel Y, Taleb M, Plestan F. A novel adaptive-gain supertwisting sliding mode controller: methodology and application[J]. Automatica, 2012, 48(5): 759-769.

[14] Guo Y, Song S. Adaptive finite-time backstepping control for attitude tracking of spacecraft based on rotation matrix[J]. Chinese Journal of Aeronautics, 2014, 27(2): 375-382.

[15] Liu Y, Zhang T, Song J, et al. Adaptive spacecraft attitude tracking controller design based on similar skew-symmetric structure[J]. Chinese Journal of Aeronautics, 2010, 23(2): 227-234.

[16] Farrell J A, Polycarpou M, Sharma M, et al. Command filtered backstepping[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395.

[17] 董朝阳, 路遥, 王青. 高超声速飞行器指令滤波反演控制[J]. 宇航学报, 2016, 37(8): 957-963.[Dong Chao-yang, Lu Yao, Wang Qing. Command filtered backstepping control for hypersonic vehicle[J]. Journal of Astronautics, 2016, 37(8): 957-963.]

[18] Hu J, Zhang H. Immersion and invariance based command-filtered adaptive backstepping control of VTOL vehicles[J]. Automatica, 2013, 49(7): 2160-2167.

[19] 宋申民, 郑重, 苏烨. 控制受限的编队航天器鲁棒自适应控制[J]. 宇航学报, 2014, 35(12): 1422-1429.[Song Shen-min, Zheng Zhong, Su Ye. Robust adaptive control of spacecraft formation flight under control constraint[J]. Journal of Astronautics, 2014, 35(12): 1422-1429.]

[20] Lu K, Xia Y. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence[J]. Automatica, 2013, 49(12): 3591-3599.

[21] Hu Q, Li B, Qi J. Disturbance observer based finite-time attitude control for rigid spacecraft under input saturation[J]. Aerospace Science and Technology, 2014, 39: 13-21.

[22] Shtessel Y B, Moreno J A, Plestan F, et al. Super-twisting adaptive sliding mode control: a Lyapunov design[C]. The 49th IEEE Conference on Decision and Control, Atlanta, USA, December 15-17, 2010.

[23] Li C, Ma G. Adaptive backstepping control for attitude tracking of a spacecraft[C]. IEEE International Symposium on Industrial Electronics, Vigo, Spain, June 4-7, 2007.

Super-TwistingObserverBasedFinite-TimeBacksteppingAttitudeControlforaCombinedSpacecraft

MA Guang-fu1, GAO Han1, LV Yue-yong1, SONG Ting2, YUAN Jian-ping3

(1. Department of Control Science and Engineering, Harbin Institute of Technology, Harbin 150001, China; 2. Shanghai Aerospace Control Technology Institute, Shanghai 200233, China; 3. School of Astronautics,Northwestern Polytechnical University, Xi’an 710072, China)

A novel finite-time controller integrated with a disturbance observer is proposed for a combined spacecraft, which is composed of a service spacecraft and a target spacecraft with large uncertainty of inertia momentum. Firstly, a modified super-twisting disturbance observer is designed so that the reconstruction of the generalized disturbances in terms of the inertia uncertainty and the external disturbance is accomplished in finite time. Then, with the reconstructed information, a finite-time controller is synthesized with the backstepping method. Besides, the command filter is also introduced to the finite-time controller which can improve the control performance. And the closed-loop system/state is proved to be finite-time stable. The numerical simulations validate the effectiveness and feasibility of the proposed control scheme.

Combined spacecraft; Super-twisting disturbance observer; Finite-time; Backsteppting attitude control; Command filter

V448.22

A

1000-1328(2017)11- 1168- 09

10.3873/j.issn.1000- 1328.2017.11.005

2017- 04- 11;

2017- 08- 03

国家自然科学基金(61603114，61673135)；国家重点基础研究发展计划(613320)

马广富(1963-)，男，教授，主要从事航天器导航制导与控制、最优控制等方面的研究。

通信地址：哈尔滨工业大学327信箱(150001)

电话：(0451)86402726

E-mail: magf@hit.edu.cn

吕跃勇(1983-)，男，助理研究员，主要从事航天器导航制导与控制、航天器在轨服务、编队飞行控制等方面的研究。本文通信作者。

通信地址：哈尔滨工业大学327信箱(150001)

电话：(0451)86418320-322

E-mail: lvyy@hit.edu.cn