基于电磁力的集群航天器构形维持自抗扰控制
杨茗棋,胡 敏,杨雅君,郭光衍
(1.航天工程大学航天装备系,北京 101416;2. 航天工程大学航天指挥系,北京 101416)
基于电磁力的集群航天器构形维持自抗扰控制
杨茗棋1,胡 敏2,杨雅君2,郭光衍1
(1.航天工程大学航天装备系,北京 101416;2. 航天工程大学航天指挥系,北京 101416)
针对基于电磁力的集群航天器构形控制强非线性和模型不确定性的问题,提出一种无需线性化或解耦便能够实现构形维持的自抗扰控制方法(ADRC)。首先建立远场电磁力/力矩模型和集群航天器相对运动动力学模型;在此基础上,通过设计由最速跟踪微分器(TD)、非线性扩张状态观测器(NLESO)及非线性反馈控制律(NLSEF)组成的自抗扰控制器,实现集群航天器期望相对运动位置、速度的实时估计,同时能够对模型不确定性和外部干扰进行估计和补偿。仿真结果表明,本文设计的控制器能够实现基于电磁力的集群航天器构形维持高精度控制,满足集群航天器构形维持控制的控制要求,其快速性和抗扰性都明显优于有限时间控制(FTC)。
集群航天器;电磁力控制;构形维持;自抗扰控制;扩张状态观测器
0 引 言
传统分布式航天器相对运动控制主要依靠推力器,存在推进剂消耗限制任务寿命、近距离羽流可能污染光学载荷、控制不连续等问题,学者们提出利用航天器之间产生的可控场力进行相对运动控制,可控场力包括库仑力[1]、flux-pinned效应力、电磁场力等,其中电磁场力是目前研究较为系统、应用更为明确的解决方案。电磁编队飞行是一个较新的概念,采用三个正交的高温超导线圈实现卫星编队的相对控制[2]。集群航天器[3]这一概念是所有分布式航天器概念中最新提出的,基于电磁力的集群航天器与整星相比可靠性更高、成本更低、灵活性更强。针对集群航天器的电磁控制、电磁交会对接和电磁编队在模型建立、控制方法的选取、作用机理等方面区别不大,因此可以互相借鉴。
电磁控制对象具有强非线性、强耦合性、远场模型不确定性的特点。由于系统线性化的前提条件是要求非线性动力学模型准确,但这一前提条件在控制工程实践中很难满足;目前采用的非线性控制方法虽然控制精度较高,但设计较复杂、计算量大[4]。自抗扰控制不仅设计方法简单,而且针对非线性、强耦合的系统有很好的控制效果;无需将系统线性化直接进行设计,避免了需要准确的动力学模型,且工程可实现性强。
自抗扰控制技术在很多领域都有非常广泛的应用[5],但在航空航天领域中,这种控制方法多被应用于姿态控制[6],关于相对运动控制的研究较少。文献[7]全面比较了针对航天器姿态的自抗扰控制与滑模控制的性能,对比分析得出自抗扰控制器具有更强的抗干扰能力和鲁棒性。文献[8]提出了一种针对电磁对接的新型控制器,该控制器结合了人工势能控制、Lyapunov稳定性理论和扩张状态观测器(Extended state observer, ESO)的优点。文献[9]采用自抗扰控制方法进行空间交会对接轨道控制,但该问题中的动力学模型与航天器相对运动动力学模型相比较简单。文献[10]通过分别设计主、从航天器的自抗扰控制器解决了航天器编队问题,但是没有与其他控制方法进行比较,不能够充分突出自抗扰控制技术的优势。
本文通过设计一种自抗扰控制器,对基于电磁力的集群航天器进行轨道控制,实现集群航天器相对构形维持的自抗扰控制。首先建立了电磁力/力矩模型和航天器相对运动动力学模型;然后将两模型结合作为控制对象进行自抗扰控制器设计;最后通过仿真校验自抗扰控制器的有效性,并与有限时间控制器的性能进行对比分析和抗扰性仿真分析,得出结论。
1 电磁力/力矩模型建立
电磁力/力矩模型是研究电磁力系统动力学和控制问题的基础。电磁作用力和力矩建模主要依据电磁场的基本理论。根据毕奥-萨法尔定律,可以求出载流线圈在空间某点产生的磁感应强度,进而根据安培定律,求得线圈在磁场中受到的电磁力[11]。
Schweighart[12]提出了近场模型、中场模型和远场模型三种星间电磁力模型,其中远场模型忽略线圈尺寸,从数学上看是近场模型的一阶线性化,便于计算和控制设计。假设两电磁线圈中心距超过线圈半径6.76倍时,该种模型误差小于10%[13]。当两个载流线圈相距较远时,可以看作两个磁偶极子,远场模型中两个磁偶极子的三维示意图如图1所示。
磁偶极子的强度μ表示为:
(1)
式中:n为线圈匝数,I为线圈电流,Rc为线圈半径。磁偶极子的方向与线圈电流方向符合右手法则。
假设共有N个航天器,第j个航天器在第i个航天器的位置上产生的磁场强度可以表示为:
(2)
式中:rij是第i个航天器和第j个航天器的相对位置矢量,rij是rij的模,μj表示安装在第j个航天器上的三个正交线圈产生磁矩的和。
第j个航天器对第i个航天器的电磁力和力矩可以表示为[13]:
(3)
将式(2)代入式(3)可得电磁力和力矩表达式为:
(4)
(5)
由式(4)和式(5)可知,电磁力和力矩分别与两航天器距离的四次方和三次方成反比,因此电磁力/力矩模型具有强非线性。对基于电磁力的集群航天器的控制,实际上是对线圈内电流的控制。通过控制电流改变电磁力时,电磁力矩也会随之改变,两者耦合使控制与期望结果产生偏差。因此,电磁力/力矩模型具有非线性、强耦合和模型不确定的特点。
为便于分析,本文假设利用反作用飞轮完成航天器的姿态控制,在建模过程中不考虑电磁力矩对相对运动的影响。本文将电磁远场模型的不确定性视为外界总扰动的一部分,通过自抗扰控制器中的非线性反馈控制律进行补偿,提高了计算精度。
2 航天器相对运动动力学模型
航天器近距离相对运动一般均采用Hill模型,基本都以参考航天器的质心轨道坐标系为参考系建立,且假设参考航天器沿近圆轨道运动[14]。然而,由于参考航天器实时受到星间电磁力作用,无论是电磁装置间相对位置/姿态变化,还是电磁装置磁矩矢量变化,都会引起两航天器运动状态的改变,其轨道为非开普勒类型。对于电磁力控制集群航天器,星间电磁力/力矩属于内力/力矩范畴,具有不改变系统质心运动和角动量、机械能守恒等特性,因此本文基于Hill模型,以航天器系统质心(Center of mass,CoM)作为参考坐标系,建立基于电磁力的集群航天器相对运动模型,如图2所示。相对运动模型建立过程中考虑多种摄动力,包括地球非球形J2项摄动、大气阻力摄动、潮汐摄动、太阳光压摄动等。由于星间电磁力不影响系统质心运动状态,航天器系统质心的运动轨迹可认为一直保持为圆轨道。
令参考航天器和环绕航天器相对于系统质心参考系的位置矢量分别表示为
(6)
则环绕航天器相对参考航天器的位置、速度及加速度矢量满足
(7)
航天器系统质心的轨迹为圆轨道,即参考航天器和环绕航天器相对于系统质心参考系的运动满足Hill模型假设。基于Hill模型分别建立参考航天器和环绕航天器相对系统质心参考系的动力学模型:
(8)
(9)

(10)
将式(9)与式(8)相减,得到集群航天器系统相对运动动力学模型:
(11)
式中:fd为等效干扰加速度,fd=fCd-fTd。
由集群航天器系统相对运动动力学模型可以看出,每个轴的动力学模型都是非线性的,且各轴相互耦合,这给控制律的设计带来了困难。本文通过对每个轴分别设计自抗扰控制器,无需将模型线性化和解耦,解决了系统非线性和强耦合问题。
3 自抗扰控制器设计
首先,将航天器相对运动动力学模型(11)中每个轴的相对运动动力学模型化简为
(12)

(13)
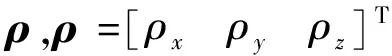
首先设计跟踪微分器,对航天器系统期望相对位置进行跟踪并对其微分量(即期望相对速度)进行计算。设计的跟踪微分器(Tracking differentiator, TD)为:
(14)
式中:h为采样时间;r0为决定过渡过程快慢的参数;v1,v2分别为x轴期望相对位置ρd x的跟踪量及其微分;最速函数ffast(x1,x2,r0,h)的表达式为
(15)
基于航天器的相对构形,能够推导出两航天器间的相对位置,将三个轴的相对位置ρd作为期望量分别输入各轴的自抗扰控制(Active disturbance rejection control, ADRC)器。以x轴为例,跟踪微分器能够实时跟踪相对位置,得到该轴期望相对位置ρd x的跟踪量v1,并实时计算出期望相对速度v2。
设计离散的三阶非线性扩张状态观测器(Nonlinear extended state observer, NLESO):
因为信息不畅通等原因[3],这些仪器设备往往只在课题组或学院内部使用,存在闲置浪费现象,专业化服务能力也有待提高。另一方面,一些刚刚入校的年轻教师因为经费不足,没有能力购买需要的科研设备[4];有些院系和科研院所有跨学科跨行业科研的需求;有些企业或个人因为技术创新研究或其他原因,也需要仪器设备,社会各界对于科研设施与仪器设备的开放共享具有广泛而迫切的需求。
(16)


(17)
利用NLESO输出的估计量z3,通过设计非线性误差反馈控制律,实现对外界干扰和系统模型不确定性进行实时补偿,如下所示:
(18)
式中:ξ1,ξ2是观测量z1,z2的误差;c为误差反馈因子,在误差反馈中起着阻尼的作用;r为非线性误差反馈控制律中决定过渡过程快慢的参数;h1为精度因子,决定跟踪目标值的跟踪精度;u0为误差反馈控制律。
将相对位置、速度的期望值与观测值相减得到相对位置误差e1和相对速度误差e2,通过设计非线性反馈控制律u0,最终得到自抗扰控制器的控制量uA x,包括两部分:一部分是基于系统状态误差设计的非线性反馈控制律,另一部分是未知系统模型和扰动的状态观测值的补偿[10]。最终实现反馈误差趋近于零,即航天器间的相对位置、速度由初始相对位置、速度达到期望相对位置、速度。
由于自抗扰控制器中参数较多,参数整定较难。本文根据文献[15]提出的方法进行参数整定,如式(19)所示,并进行适当调整,最终选取ADRC控制器参数。
(19)
4 仿真校验
本节通过仿真校验设计的自抗扰控制器的有效性,并从控制效果和抗扰性能两方面将ADRC与有限时间控制(Finite-time control,FTC)进行对比分析。
当两航天器的相对位置误差大于2.5 m时开始进行控制,由仿真结果可知,控制器从第9390 s起控。总仿真时间为4 h,采样周期h=1 s。每个携带电磁线圈的航天器的质量均为36 kg[13]。假设参考航天器和环绕航天器的磁矩方向共轴。
表1至表3分别给出了参考航天器的初始轨道参数,集群航天器相对构形参数和Hill系中初始相对构形参数。

表1 参考航天器的初始轨道参数Table 1 Initial orbital elements of the reference orbit

表2 集群航天器间的相对构形参数Table 2 Spacecraft cluster configuration parameters
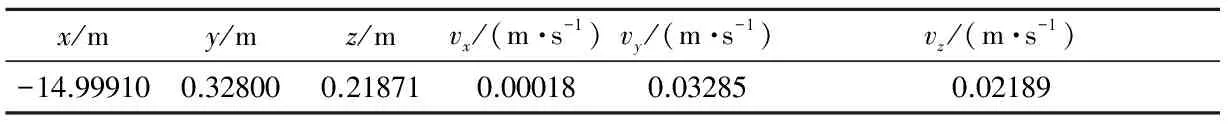
表3 Hill系中初始相对构形参数Table 3 Initial relative states in the Hill frame
4.1ADRC与FTC对比分析
三轴的控制器设置相同参数,ADRC的设计参数为:

表4 ADRC的设计参数Table 4 The ADRC parameters
有限时间控制律及其参数分别如式(20)和表5所示[13]。
(20)

表5 有限时间控制的参数Table 5 The FTC parameters
不考虑外界干扰时,自抗扰控制器的控制效果如图4所示。由图4(a)可知,理想情况下,两航天器的相对运动轨迹最终与期望相对运动轨迹重合,即实现了集群航天器系统的构形维持。由图4(b)和图4(c)可知,ADRC各轴的控制量和两航天器间的电磁力最终都趋近于零。由此,验证了ADRC的有效性。
无外界干扰时,将ADRC与FTC的控制效果进行对比分析。各轴相对位置误差和到达稳态的时间分别如图5和表6所示。

表6 无外界干扰时控制器各轴的调整时间Table 6 Transition time of relative position error without external disturbance
由图5和表6可知,在无外界干扰的自抗扰控制下,航天器系统相对位置误差的调整时间远小于有限时间控制;然而其超调量较大,但在无干扰条件下,均不超过1 m,在允许范围内。
与有限时间控制相比,自抗扰控制的控制量较大,由图4(b)可知,最大控制量为x轴的控制量,约3 m/s2,控制精度能够满足针对基于电磁力的集群航天器的轨道控制要求,因此ADRC在实际控制中更具有优势。
进一步分析ADRC和FTC两种控制器的控制律,如图6所示。由图6可知,与FTC相比,ADRC的控制律变化曲线较平滑,而FTC的抖振现象较严重,容易激发系统的高频未建模动态。同时FTC控制律设计时引入了相对位置及其误差的微分信号,但在工程实践中,没有合适的微分器能够直接测量实际行为变化速度;而ADRC控制器中利用跟踪微分器提取微分信号,便于工程实现。
4.2抗扰性对比仿真分析
对ADRC和FTC进行抗扰性仿真分析,仿真中从控制器起控时开始,假设各轴外界干扰量(包括不可预测和工程实际中的干扰总和)为d=0.001sin(0.05t) m/s2。存在外界干扰时,得到两种控制器作用下各轴相对位置误差和到达稳态的时间分别如图7和表7所示。
对比分析图5和图7、表6和表7可知,存在外界干扰与理想情况相比,两控制器的调整时间和稳态误差均有所增加,但是FTC相比之下受到外界干扰的影响较大,调整时间增加较多,而ADRC控制系统受到外界干扰后仍能够较快实现构形维持,且各轴调整时间增加量不大。综上所述,ADRC的抗扰性较FTC更强。
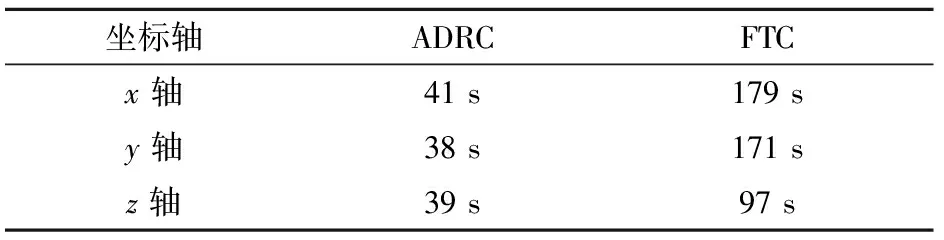
表7 存在外界干扰时控制器各轴的调整时间Table 7 Transition time of relative position error with external disturbance
进一步分析存在外界干扰时,外界干扰及ESO对包括外界干扰和模型不确定性的总扰动的估计,如图8所示。从图8可以看出,ADRC中的NLESO能够很好地估计外界干扰,x,y,z轴分别经过43 s,55 s,54 s便可实现总扰动的有效估计。
上述抗扰性试验结果表明,ADRC与FTC相比不仅具有较强的抗扰性,而且能够对总扰动进行实时估计并补偿。
5 结 论
针对基于电磁力的集群航天器系统复杂性和模型不确定性的问题,设计了一种进行构形维持控制的自抗扰控制方法,并验证了该方法的有效性。该控制算法设计方法简单,无需将模型线性化或解耦即可进行控制律设计,且具有工程可实现性;但是参数较难整定,且控制量较大。在此基础上比较自抗扰控制与有限时间控制的控制效果,并进行了抗扰性对比仿真分析。仿真结果表明,该控制器不仅能够实现对期望相对运动位置、速度的实时估计,同时还能够对包括模型不确定性和外部干扰的总扰动进行估计并补偿,控制精度能够满足对基于电磁力的集群航天器的轨道控制要求,其快速性和抗扰性都明显优于有限时间控制。
[1] 王婷,张羽飞. 等质量立体五星库伦编队飞行的分析与控制[J]. 宇航学报, 2015, 36(11): 1279-1288.[Wang Ting, Zhang Yu-fei. Analysis and control for three dimensional five-satellite coulomb formation flight in geostationary earth orbit[J]. Journal of Astronautics, 2015, 36(11): 1279-1288.]
[2] Miller D W, Sedwick R J, Kong E M C, et al. Electromagnetic formation flight for sparse aperture telescopes[C]. IEEE Aerospace Conference, Big Sky, USA, March 9-16, 2002.
[3] Schweighart S A, Sedwick R J. Explicit dipole trajectory solution for electromagnetically controlled spacecraft clusters[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1225-1235.
[4] 黄一, 薛文超, 赵春哲. 自抗扰控制纵横谈[J]. 系统科学与数学, 2011, 31(9): 1111-1129.[Huang Yi, Xue Wen-chao, Zhao Chun-zhe. Active disturbance rejection control: methodology and theoretical analysis[J]. System Science and Math Sciences, 2011, 31(9): 1111-1129.]
[5] 赵玉龙, 沈怀荣, 任元. 幅值锁定型超流体陀螺模糊自抗扰控制系统设计[J]. 宇航学报, 2016, 37(5): 562-569.[Zhao Yu-long, Shen Huai-rong, Ren Yuan. Design of fuzzy active disturbance rejection control system for amplitude locked superfluid gyroscope[J]. Journal of Astronautics, 2016, 37(5): 562-569.]
[6] 李顺利, 李立涛, 杨旭. 柔性多体卫星自抗扰控制系统的研究[J]. 宇航学报, 2007, 28(4): 76-81.[Li Shun-li, Li Li-tao, Yang Xu. Active disturbance rejection control for flexible multi-body satellite system[J]. Journal of Astronautics, 2007, 28(4): 76-81.]
[7] 康莹, 李东海, 老大中. 航天器姿态的自抗扰控制与滑模控制的性能比较[J]. 控制理论与应用, 2013, 20(12): 1623-1629.[Kang Ying, Li Dong-hai, Lao Da-zhong. Performance comparison of active disturbance rejection control and sliding mode control in spacecraft attitude control[J]. Control Theory amp; Application, 2013, 20(12): 1623-1629.]
[8] Zhang Y W, Yang L P, Zhu Y W, et al. Self-docking capability and control strategy of electromagnetic docking technology[J]. Acta Astronautica, 2011, 69: 1073-1081.
[9] 李凯凯. 基于自抗扰的空间交会对接轨道控制研究[D]. 合肥: 中国科学技术大学, 2015.[Li Kai-kai. Study on the orbit control of space rendezvous and docking using active disturbance rejection control[D]. Hefei: University of Science and Technology of China, 2015.]
[10] 朱敏. 太阳帆航天器动力学与控制研究[D]. 合肥: 中国科学技术大学, 2016.[Zhu Min. Dynamics and control of solar sail spacecraft[D]. Hefei: University of Science and Technology of China, 2016.]
[11] 胡敏, 黄勇, 李小将. 卫星编队飞行协同控制及仿真[M]. 北京: 国防工业出版社, 2016.
[12] Schweighart S A. Electromagnetic formation flight dipole solution planning[D]. Cambridge: Massachusetts Institute of Technology, 2005.
[13] Zeng G Q, Hu M. Finite-time control for electromagnetic satellite formations[J]. Acta Astronautica, 2012, 74: 120-130.
[14] Ahsun U. Dynamics and control of electromagnetic satellite formations in low earth orbits[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, keystone,USA, August 21-24, 2006.
[15] 韩京清. 自抗扰控制技术—估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2016.
ActiveDisturbanceRejectionControlforConfigurationMaintenanceofElectromagneticallyControlledSpacecraftCluster
YANG Ming-qi1, HU Min2, YANG Ya-jun2, GUO Guang-yan1
(1.Department of Space Equipment, Space Engineering University,Beijing 101416,China;2.Department of Space Command,Space Engineering University,Beijing 101416,China)
An active disturbance rejection control (ADRC) method for configuration maintenance that does not require linearizing or decoupling is proposed for the electromagnetically controlled spacecraft clusters with nonlinearity and electromagnetic force model uncertainty. Firstly, the far-field electromagnetic force/torque and spacecraft relative models are presented. A time-optimal tracking differentiator (TD), a nonlinear extended state observer (NLESO) and nonlinear state error feedback (NLSEF) control law are then designed. The designed ADRC can estimate the expected relative positions and velocities in real time, observe the relative positions and velocities, and also estimate and compensate the model uncertainty and disturbances online. Finally, the simulation results indicate that the ADRC is effective and can achieve high precision control. In contrast to the finite-time control (FTC), the ADRC performs much superior in celerity and ability in disturbance rejection.
Spacecraft cluster; Electromagnetic control; Configuration maintenance; Active disturbance rejection control; Extended state observer
V448.2
A
1000-1328(2017)11- 1204- 08
10.3873/j.issn.1000- 1328.2017.11.009
2017- 05- 27;
2017- 08- 31
国家自然科学基金(61403416)
杨茗棋(1993-),女,硕士生,主要从事集群航天器动力学与控制方面的研究。
通信地址:北京3380信箱79号(101416)
电话:(010)66364652
E-mail: 1110410320@hit.edu.cn

