固体导弹助推段自抗扰制导控制一体化设计方法

聂文明，李惠峰

(北京航空航天大学宇航学院, 北京 100191)

固体导弹助推段自抗扰制导控制一体化设计方法

聂文明，李惠峰

(北京航空航天大学宇航学院, 北京 100191)

针对存在建模误差及外部干扰情况下的固体导弹助推段制导控制一体化(IGC)设计问题，给出一类自抗扰制导控制一体化设计方法。首先考虑质心运动与绕质心运动间的耦合，结合轨迹线性化方法建立了面向控制的固体导弹助推段制导控制一体化设计模型。采用扩张状态观测器(ESO)实时估计系统建模误差与外部干扰，进而基于反步法结合反馈线性化方法,提出一类考虑质心运动与绕质心运动间的耦合作用的自抗扰制导控制一体化设计方法，并通过Lyapunov稳定性理论证明了该制导控制一体化设计方法可保证闭环系统的稳定性，解决了传统制导控制系统分离设计方法无法保证闭环系统稳定性的问题。最后，数值仿真校验了本文所提的助推段自抗扰制导控制一体化(ADRIGC)设计方法的控制性能及抗干扰性能。

助推段制导控制一体化模型；制导控制一体化；扩张状态观测器；反步控制；固体导弹

0 引 言

制导控制一体化(Integrated guidance and control, IGC)设计是一种从整体上设计导弹制导控制系统的思想。不同于传统的设计方法，IGC充分考虑制导系统与控制系统的耦合关系，把二者作为一个整体考虑，根据导弹质心运动信息直接产生执行机构控制指令[1]，既能减少设计周期和成本，还能弱化对导弹机动性的约束，避免导弹的失稳现象，改善导弹控制中的过程控制特性及终端精度[2-3]。

传统的导弹制导与姿态控制系统分离设计思想可概括为：基于时域分离假设，将制导控制系统分为制导回路与姿控回路，忽略质心运动与绕质心运动间的耦合，分别设计制导律与姿态控制律，最后将设计好的子系统整合后，若整体性能未达到期望的要求，则需重新设计每个子系统，反复迭代，直到满意为止[4]。为了改善跟踪性能，各类非线性现代控制理论被用于制导律与姿态控制律的设计，如鲁棒控制[5]、滑模控制[6]、增益调度控制[7]、反步控制[8]及有限时间控制[9]等，但由于分离设计思想本身的局限性，得出的控制系统只能改善各子系统自身控制性能，而无法保证整合后的制导控制系统总体的稳定性与控制性能。

IGC设计则把制导系统和控制系统视为整体，设计过程中不依赖于时域分离假设，即使在存在不确定性或导弹机动的情况下，也不会出现失稳现象，从而保证制导精度[10]。自Williams等[1]于20世纪80年代提出制导与控制一体化设计以来，许多学者依据这种整体设计的思想开展了研究工作，尤其是近30年来，制导与控制一体化设计取得了较丰富的研究成果。最早的制导控制一体化设计采用了线性最优控制方法[1，11]，但是由于导弹的制导控制系统自身的强非线性与强耦合，线性控制方法不能满足设计要求。因此，基于非线性最优控制理论的IGC设计方法被提出，为解决Hamilton-Jacobi-Bellman (HJB)方程难以求解的问题，各国学者在求解制导控制一体化最优控制问题时，分别采用了两种数值解法：状态依赖Riccati方程法[12]和θ-D方法[13]。上述设计方法均基于复杂的导弹六自由度非线性动力学方程，存在难以在线实时求解的问题，并且设计中未考虑未建模动态或外部扰动对控制系统性能的影响。此后，上述问题被很大程度地简化，出现了近似一体化的思路[9，14-15]，该思路将姿态角动态近似为某类参考模型，并在设计制导律时将该近似模型动态考虑在内，但其实际上仍是一种分离设计的思路，与传统设计思路没有本质区别。为解决上述问题，各国学者分别从制导控制一体化模型设计与一体化控制方法设计两个角度对制导控制一体化设计问题展开了广泛研究[16]。目前主要有两类一体化模型：相对位置模型和视线角模型[16]，基于这两类模型，各国学者分别采用反步控制[17-18]、自抗扰控制[19]、滑模控制[20]、自适应控制[21]和鲁棒控制[22]等方法给出了制导控制一体化控制设计方法。

现有IGC设计方法的研究均针对导弹打击段展开，为解决导弹助推段的制导控制一体化设计问题，则需要结合导弹上升段飞行力学特性及控制需求，同时考虑模型复杂度、方法复杂度、系统稳定性、抗干扰特性等问题，给出可行的一体化设计方法。本文以单喷管两级固体导弹为研究对象，针对其助推段IGC设计问题展开研究，主要创新点如下：1)结合助推段飞行力学特性和控制需求，引入侧滑角以主动控制固体导弹助推段速度，并考虑质心运动与绕质心运动间的耦合作用，建立了助推段制导控制一体化设计模型，进而采用轨迹线性化方法，将原非仿射模型转化为仿射模型，最终给出了面向控制的固体导弹助推段IGC设计模型；2)采用反步法设计一体化设计框架，结合反馈线性化方法设计得到了助推段IGC控制器，解决了传统设计方法无法保证制导控制综合系统稳定性的问题，并从理论分析的角度证明了本文提出的自抗扰IGC(Active disturbance rejection IGC, ADRIGC)设计框架可实现闭环系统的稳定；3)基于扩张状态观测器(Extended state observer, ESO)设计了具有自抗扰特性的助推段制导控制一体化控制系统[19]，提高了闭环控制系统的抗干扰性能，改善了存在建模误差及外界干扰情况下的过程跟踪性能及终端精度。

1 面向控制的助推段IGC设计模型

本节首先给出固体导弹助推段质心运动模型与绕质心运动模型，然后针对模型存在的非仿射问题，采用轨迹线性化方法将模型转化为仿射系统，得到面向控制的助推段IGC设计模型。

1.1助推段IGC运动模型

单喷管固体导弹的中心喷管仅能提供俯仰力矩与偏航力矩，而在实际设计中，通常采取滚转稳定控制策略，通过安装滚转反作用控制系统(Reaction control system,RCS)等方式保证滚转通道姿态稳定。因此本文针对其俯仰通道与偏航通道的IGC设计问题展开研究。基于上述分析，建立如下标称模型：

(1)

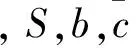
需要指出的是，对于固体导弹而言，无法通过改变推力大小的方式实现对速度的控制,因此区别于文献[21]等文献中的助推段质心运动模型，本文给出的助推段IGC运动模型将侧滑角引入质心运动方程，以实现对速度的主动控制。另一方面，攻角、侧滑角在运动方程中以非仿射的形式出现，增加控制自由度的同时也增加了控制系统设计的难度。

1.2面向控制的助推段IGC设计模型

为利用并补偿质心运动与绕质心运动之间的耦合作用，本节首先建立考虑上述耦合的助推段IGC设计模型；进而为解决IGC设计模型存在的非仿射问题，结合导弹助推段存在标称轨迹的特点，采用轨迹线性化方法将原非仿射IGC设计模型转化为仿射IGC设计模型，得到了面向控制的IGC设计模型。

记vθ=vsinθ，为方便表述并考虑飞行环境干扰，将式(1)重写为如下紧凑形式：

(2)

(3)

(4)

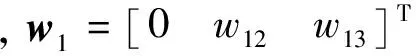
(5)

联立式(2)、式(4)，可得如下面向控制的助推段IGC设计模型：

(6)

2 控制器设计

本节将基于式(6)所示的面向控制的IGC设计模型，首先假设建模误差及外界干扰已知，给出助推段IGC设计方法，然后通过设计ESO，实时估计未知的建模误差与外界干扰并反馈至控制器，得到助推段ADRIGC设计方法，最后通过Lyapunov稳定性理论，证明上述ADRIGC控制器可保证闭环系统的稳定性。

2.1助推段IGC设计方法

引入辅助控制量x1d,x2d,x3d，其中x1d=x1nom为助推段标称轨迹，x2d,x3d为IGC设计中待设计的量，稍后将给出定义。

定义如下误差向量：

(7)

联立式(6)、式(7)可得如下误差动态方程：

(8)

基于反步法，分别利用PD控制与反馈线性化控制可得如下IGC控制器：

(9)

x2d,x3d分别满足如下方程：

(10)

式中：K1∈R2×3,K2∈R2×2,K3∈R2×2,为待设计控制器参数矩阵。

注1. 式(10)所示x2d表示IGC设计中实际的期望姿态角指令，而在传统的分离设计中，期望姿态角指令为x2nom，两者之间的不同在于Δx2d，而Δx2d是对质心运动与绕质心运动之间的耦合起补偿作用的项，由此设计得到的姿态角指令x2d可实现对质心运动跟踪误差的主动控制，而传统分离设计思路下的姿态控制器未考虑上述耦合，姿态控制器的改进也仅能实现对x2nom的跟踪，而无法影响质心运动的跟踪误差。

2.2自抗扰IGC设计方法

式(9)所示的IGC控制器中含有未知建模误差w1和外干扰项di,i=1,2,3。为使控制系统具有实时补偿上述不确定项的能力，需要实现对上述未知项的实时估计。本节采用ESO实现对各不确定项的实时观测[23]，以保证式(9)所示IGC控制器在工程应用中的可实现性。

(11)

(12)

则可设计如下ESO：

(13)

基于ESO观测结果，式(9)中总扰动w1+d1,d2及d3可由其观测值代替，从而可得如下ADRIGC控制器:

(14)

基于ESO观测值，x2d,x3d可写为如下形式：

(15)

2.3稳定性证明

引理1[24]. 在式(12)所示ESO中，设计如下形式的观测器参数：

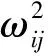
(16)

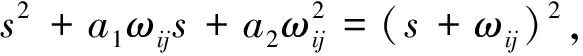
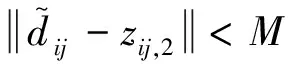
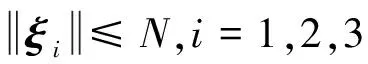
定理1. 对于控制器参数矩阵K1∈R2×3，K2∈R2×2,K3∈R2×2。取c1为K1,K2,K3中各元素最小值，若满足K1gt;0,K2gt;0,K3gt;0且c1gt;3M/N，则式(14)所示的ADRIGC控制器可实现系统的闭环稳定。

证. 定义Lyapunov函数：

(17)

对式(17)求导可得：

(18)

将式(8)、式(14)、式(15)代入式(18),可得：

(19)

基于假设1与假设2可得：

(20)

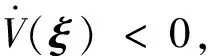
3 仿真校验

本节将给出仿真结果及分析，首先在无外部干扰的情况下，对比分析了基于传统设计思路[25]与IGC设计思路的两类轨迹跟踪控制器性能，校验本文提出的IGC设计方法的有效性；然后针对不同气动干扰情况进行IGC控制系统仿真，校验了基于ESO的ADRIGC控制器的抗干扰特性。

本节仿真以二级固体导弹为研究对象，导弹起飞后68 s进行一、二级分离，抛弃第一级干重，终端高度76 km，终端速度3758 m/s，第一级控制力矩约束为：|Mcb1|lt;866590 N·m，第二级控制力矩约束|Mcb2|lt;3341210 N·m。以下仿真算例中，仿真步长为0.01s，控制器设计参数与观测器设计参数均一致，具体如下：

3.1IGC设计有效性仿真校验

为考察IGC设计思路相对传统设计思路的优点，分别基于两种思路设计轨迹跟踪控制器，并在不考虑大气扰动的情况下进行数值仿真，两类控制器均采用标称控制器，即未引入ESO观测值(以式(14)、(15)所示的IGC控制器为例，标称IGC控制器即设置zij=0)。其数值仿真结果如图1～4所示(注.图1～4中，u0,uIGC分别代表基于传统设计和基于IGC设计的控制器)。

从图1和图2可以看出，基于IGC设计的控制系统实现了对标称轨迹的跟踪，同时保证了导弹姿态的稳定。而基于传统设计思路的控制系统虽然对攻角和侧滑角指令的跟踪效果优于IGC设计，但是由于传统设计思路中未考虑制导与姿控系统的耦合，设计的控制器无法在维持姿态稳定的同时保证轨迹跟踪的精度，因此导致助推段跟踪误差越来越大。从图4可以看出，IGC设计可保证助推段跟踪误差绝对值维持在较小范围内(最大高度跟踪误差：160 m，最大速度跟踪误差：8 m/s)，而传统设计高度跟踪误差则明显较大，其中高度跟踪误差已超出可接受范围(最大高度跟踪误差：2914 m，最大速度跟踪误差：40 m/s)。而图3所示的控制力矩响应曲线说明整个控制过程中控制量未超出约束值。

图2给出的姿态响应曲线中，IGC控制下的侧滑角在68 s附近出现短暂波动，这是由于此时抛弃一级干重，造成的质量突变引起的。而质量突变直接影响了质心运动，导致轨迹跟踪出现误差，由式(14)、(15)可知，上述误差会产生额外的控制力矩，而基于传统设计的控制器中未考虑轨迹跟踪误差项，因此无法消除质量突变对轨迹跟踪造成的影响，如图4所示，传统设计控制下的高度跟踪误差在质量突变后以更快的速度增大，而速度跟踪误差也在此处出现波动。

此外，图4中u0的高度跟踪误差曲线从20 s处开始出现快速增长，这是因为在传统设计思路中，姿态控制器无法消除制导环因建模误差或外界干扰等导致的跟踪误差。而在本仿真算例中，尽管未考虑外界干扰，但轨迹线性化导致式(6)所示的面向控制的模型与式(1)所示的真实模型相比，存在建模误差，因此会导致制导环的跟踪误差。0～20 s内已经出现跟踪误差，若不做出补偿，将必然导致误差增加越来越迅速。传统分离设计的思路的固有缺陷使得u0无法抑制误差的增长，而基于IGC设计思路,考虑制导环与姿控环的耦合，uIGC可消除该类误差。

3.2ADRIGC设计抗干扰特性仿真校验

在试验2中，为校验基于本文所提的ADRIGC设计方法的控制系统抗干扰特性，引入大气干扰，假设气动力存在如下形式的正弦干扰(以升力为例，阻力与侧力干扰同时引入相同形式干扰)：

(21)

表1给出了不同气动干扰下高度与速度的终端值，ADRIGC即为式(14)所示的控制器，而标称IGC则未引入对建模误差及气动干扰的补偿项，由表1不难看出，自抗扰IGC控制的终端精度明显优于标称IGC，某些情况下标称IGC已经发散的情况下，自抗扰IGC的终端控制精度仍保持较好鲁棒性，说明自抗扰IGC对较大范围(较大幅值及频率范围)内的气动干扰均具有很好的抗干扰特性。

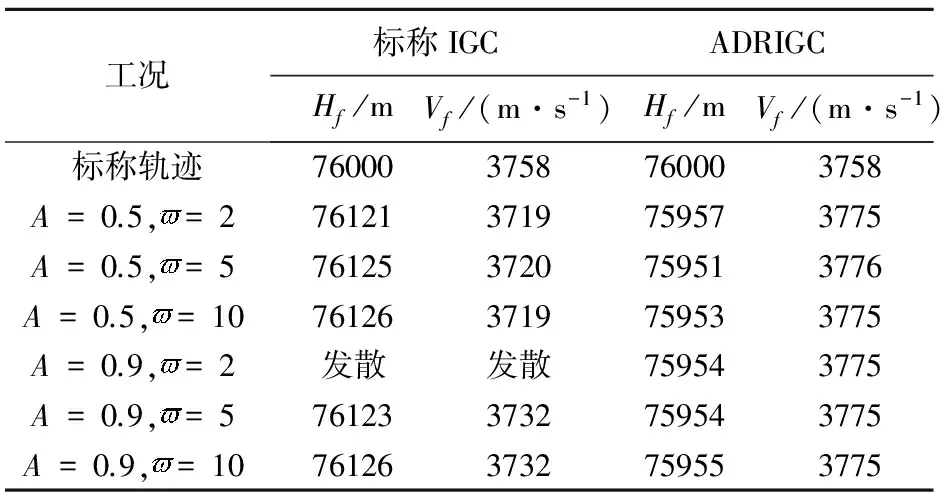
表1 不同外部干扰下的终端跟踪误差Table 1 Terminal tracking errors with different external disturbances

另外，图8中的跟踪误差明显小于图4，这是因为IGC设计方法考虑了制导环与姿控环的耦合，气动干扰与建模误差造成的轨迹跟踪误差被引入姿态环，最终进入控制器，保证跟踪误差始终处于较小范围。而ESO的引入使外部干扰与建模误差得以被实时估计并反馈至控制器，因此uADRIGC跟踪误差小于uIGC。除跟踪误差较小外，uADRIGC的姿态角响应及控制量响应均优于uIGC。进一步证明了本文所提ADRIGC设计方法的有效性。

分别利用常值与矩形波干扰模拟常值风与阵风干扰，其中常值干扰在50 s出现，幅值为气动力的0.5倍，即0.5F，F表示气动力，矩形波干扰周期为T=30 s，形式如式(22)所示。从图 9可以看出，高度与速度跟踪误差始终控制在较小范围内，进一步说明了ADRIGC的有效性与鲁棒性。

(22)

4 结 论

本文针对固体导弹助推段IGC设计问题，首先给出了考虑质心运动与绕质心运动间耦合的IGC设计模型，并采用轨迹线性化方法解决了原IGC设计模型存在的非仿射问题，最终得出了面向控制的固体导弹助推段IGC设计模型。基于上述模型提出了一类ADRIGC设计方法，与传统的分离设计方法相比，ADRIGC设计一方面保证了总体控制系统的理论稳定性，取消了迭代设计过程，简化了设计工作，弱化了设计中对导弹机动性的约束；另一方面，通过引入ESO实现了对未知项的实时估计与补偿，提高了控制精度，改善了响应品质。最终，通过理论分析与数值仿真对上述结论进行了分析与校验。

[1] Williams D, Richman J, Friedland B. Design of an integrated strapdown guidance and control system for a tactical missile[C].Guidance and Control Conference, Gatlinburg, USA， August 15-17, 1983.

[2] 董飞垚, 雷虎民, 周池军,等. 导弹鲁棒高阶滑模制导控制一体化研究[J]. 航空学报, 2013, 34(9):2212-2218.[Dong Fei-yao, Lei Hu-min, Zhou Chi-jun,et al. Research of integrated robust high order sliding mode guidance and control for missiles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9):2212-2218.]

[3] Shima T, Idan M, Golan O M. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance Control amp; Dynamics, 2012, 29(2):250-260.

[4] 程继红. 飞行器控制导引一体化设计方法研究[J]. 海军航空工程学院学报, 2006, 21(2):227-230.[Cheng Ji-hong. Research on integrated design method for air vehicle’s guidance and control[J]. Journal of Naval Aeronautical Engineering Institute, 2006, 21(2):227-230.]

[5] Yang C D, Chen H Y. NonlinearH∞Robust guidance law for homing missiles[J]. Journal of Guidance Control amp; Dynamics, 1998, 21(6):882-890.

[6] Zhou D, Mu C, Xu W. Adaptive sliding-mode guidance of a homing missile[J]. Journal of Guidance Control amp; Dynamics, 1999, 22(4):589-594.

[7] Buschek H. Full envelope missile autopilot design using gain scheduled robust control[J]. Journal of Guidance Control amp; Dynamics, 1999, 22(1):115-122.

[8] Xu B, Zhang Y. Neural discrete back-stepping control of hypersonic flight vehicle with equivalent prediction model[J]. Neurocomputing, 2015, 154: 337-346.

[9] Chwa D, Jin Y C. Adaptive nonlinear guidance law considering control loop dynamics[J]. IEEE Transactions on Aerospace amp; Electronic Systems, 2003, 39(4):1134-1143.

[10] 梁晓玲. 控制受限的导引与控制一体化设计[D]. 哈尔滨:哈尔滨工业大学, 2015.[Liang Xiao-ling. The integrated design method of guidance and control with control constraints[D]. Harbin:Harbin Institute of Technology, 2015.]

[11] Hughes T, Mcfarland M. Integrated missile guidance law and autopilot design using linear optimal control[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Dever, USA, August 14-17, 2000.

[12] Menon P K, Ohlmeyer E J. Integrated design of agile missile guidance and autopilot systems[J]. Control Engineering Practice, 2001, 9(10):1095-1106.

[13] Xin M, Balakrishnan S N, Ohlmeyer E J. Integrated guidance and control of missiles withθ-Dmethod[J]. IEEE Transactions on Control Systems Technology, 2006, 14(6):981-992.

[14] Chwa D, Jin Y C, Anavatti S G. Observer-based adaptive guidance law considering target uncertainties and control loop dynamics[J]. IEEE Transactions on Control Systems Technology, 2006, 14(1):112-123.

[15] Ju H S, Tsai C C. Longitudinal axis flight control law design by adaptive backstepping[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 43(1):311-329.

[16] 赖超, 王卫红, 熊少锋. 拦截大机动目标的三维制导控制一体化设计[J]. 宇航学报, 2017, 38(7):714-722.[Lai Chao, Wang Wei-hong,Xiong Shao-feng. Integrated guidance and control design against highly maneuvering target[J]. Journal of Astronautics, 2017, 38(7):714-722.]

[17] 孙向宇, 晁涛, 王松艳, 等. 考虑通道耦合因素的制导控制一体化设计方法[J]. 宇航学报, 2016, 37(8):936-945.[Sun Xiang-yu, Chao Tao, Wang Song-yan, et al. Integrated guidance and control design method considering channel coupling[J]. Journal of Astronautics, 2016, 37(8):936-945.]

[18] 舒燕军, 唐硕. 轨控式复合控制导弹制导与控制一体化反步设计[J]. 宇航学报, 2013, 34(1):79-85.[Shu Yan-jun, Tang Shuo. Integrated guidance and control backstepping design for blended control missile based on NDO[J]. Journal of Astronautics, 2013, 34(1):79-85.]

[19] Xue W, Huang C, Huang Y. Design methods for the integrated guidance and control system[J]. Control Theory Appl., 2013, 30(12): 1511-1520.

[20] 王建华, 刘鲁华, 王鹏, 等. 高超声速飞行器俯冲段制导控制一体化设计方法[J]. 航空学报, 2017 (3): 207-219.[Wang Jian-hua, Liu Lu-hua, Wang Peng,et al. Integrated guidance and control for hypersonic vehicles in dive phase[J]. Acta Aeronautica et Astronautica Sinica, 2017 (3): 207-219.]

[21] Erdos D, Shima T, Kharisov E, et al. L1 adaptive control integrated missile autopilot and guidance[C]. AIAA Guidance, Navigation, and Control Conference Minneapolis, Minnesota,USA, August 13-16, 2012.

[22] Yan H, Ji H. Integrated guidance and control for dual-control missiles based on small-gain theorem[J]. Automatica, 2012, 48(10):2686-2692.

[23] 韩京清. 自抗扰控制技术-估计补偿不确定因素的控制技术[M]. 北京:电子工业出版社, 2005:184-230.

[24] Zheng Q, Gao L Q, Gao Z. On validation of extended state observer through analysis and experimentation[J]. Journal of Dynamic Systems, Measurement, and Control, 2012, 134(2).

[25] Lu P. Nonlinear trajectory tracking guidance with application to a launch vehicle[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(1): 99-106.

AnActiveDisturbanceRejectionDesignMethodforAscentIntegratedGuidanceandControlofSolidMissiles

NIE Wen-ming, LI Hui-feng

(School of Astronautics, Beihang University, Beijing 100191, China)

This paper presents a novel design method of the integrated guidance and control (IGC) for the solid missiles in the ascent phase subject to modeling uncertainties and external disturbances. Firstly, an ascent model considering the coupling between the guidance and control loops is established. Then it is converted to a control oriented ascent IGC design model based on the trajectory linearization method. The extended state observer (ESO) is adopted to timely estimate the modeling uncertainties and external disturbances to make them available for feedback. Based on the backstepping and feedback control methods, an active disturbance rejection based IGC design method is proposed. The stability analysis of the closed-loop system is provided in the framework of the Lyapunov stability theory. Finally, the numerical simulation demonstrates the efficiency and robustness of the proposed active disturbance rejection integrated guidance and control (ADRIGC).

Ascent integrated guidance and control model; Integrated guidance and control design; Extended state observer; Backstepping control; Solid missile

V412.1

A

1000-1328(2017)11- 1177- 09

10.3873/j.issn.1000- 1328.2017.11.006

2017- 06- 05;

2017- 08- 27

国家重点研发计划(2016YFB1200100)

聂文明(1990-)，男，博士生，主要从事再入飞行器姿态控制方法，制导控制一体化设计方法研究。

通信地址：北京市海淀区学院路37号(100191)

电话:(010)83229527

E-mail:wenming0912@buaa.edu.cn