一种对地四重覆盖星座构型设计方法

孟少飞, 刘新学，杨 其，朱 涛

(1. 火箭军工程大学，西安710025；2. 西安测绘总站，西安710054)

一种对地四重覆盖星座构型设计方法

孟少飞1, 刘新学1，杨 其1，朱 涛2

(1. 火箭军工程大学，西安710025；2. 西安测绘总站，西安710054)

针对传统星座设计中覆盖模型求解困难，覆盖性能统计不便等问题，提出一种基于二维图的对地四重连续覆盖星座构型设计新方法。首先对传统的二维空间坐标系进行了改进，利用球面几何学分析了覆盖圆与卫星轨道的相对位置关系，建立二维图和星座网格的解析数学模型。通过对数学模型的进一步分析，归纳与总结了二维图的几何性质。将星座对纬度带的覆盖转化为对纬度带上任意点的二维图的覆盖，提出星座网格对二维图的单重和四重连续覆盖条件。在此基础上，研究四重覆盖星座构型的设计与筛选方法，从而避开了覆盖性能统计的复杂过程。最后对二维图基本理论和星座设计方法进行了实例仿真，校验了该方法的可行性。

星座构型；球面几何；二维图；四重连续覆盖

0 引 言

卫星星座是航天事业的重要领域，星座构型设计则是卫星星座研究的重要内容之一。星座构型解析设计方法的研究最早可以追溯至20世纪60年代，Walker[1]和Lang[2-3]在球面几何学的基础之上对星座构型的解析方法进行了深入的研究。之后虽然经过半个多世纪的发展，但仍然以球面几何的方法为主[4-5]。由于球面几何的复杂性和解的局限性，当卫星数量较多或覆盖情况较为复杂时，往往很难得到解析的构型设计方案。随着计算机技术的发展，基于仿真计算的现代优化算法也逐渐在星座构型设计领域得到了广泛的应用与发展[6-8]。该方法往往需要借助仿真星座的覆盖过程以统计星座的覆盖性能，因此往往计算量较大。

二维图理论出现于20世纪80年代，最早被应用于星座构型的覆盖性能分析[9]。Ulybyshev[10-13]将其应用到星座构型设计问题，从而提出一种新的构型设计思路。但其研究中依然沿用早期的二维空间坐标系，很难建立二维图的解析模型。在二维图的计算上仍然采用数值迭代的方法，在计算的快速性和精确性以及求解更复杂覆盖问题上限制了该方法的发展。而国内学者在研究星座覆盖时多采用单元统计的方法[14-15]，使用二维图进行覆盖研究的相关文献还较少。本文对这种方法进行了进一步研究，在二维图数学模型的构建、特性分析以及应用扩展上进行了深入的探讨与完善。

1 二维图基本理论

文献[10]中对二维空间的定义为：以升交点赤经Ω为x轴，以相位角u为y轴，卫星在其轨道上的位置所组成的点形成的空间。二维图则相应的为卫星对目标点可见的位置所组成的区域。设卫星轨道为圆轨道，高度为1000 km，倾角为45°，卫星最小可见角为15°；目标点经度为180°E，纬度为30°N，则卫星对目标点可见的二维图如图1所示。

当x轴采用升交点赤经时，二维图的计算需要考虑地球的旋转，其数学模型为高阶超越方程，很难用解析的方法求解，只能采用数值迭代的方法计算二维图的边界曲线。这里对二维图的坐标轴进行调整，以卫星轨道面与地球赤道的交点经度作为卫星轨道经度L，代替升交点经度Ω，从而建立了二维图的解析数学模型，提高其边界曲线计算的便利性、快速性。

按照二维图形状的不同，可以将二维图分为3类：连通凸型，连通凹型和非连通型，如图2所示。设卫星轨道倾角为i，卫星的覆盖圆半径为β，目标点的纬度为φ，则三种不同类型的二维图所对应的条件为(如图3所示)：

连通凸型：φ≥i+β

连通凹型：i-β≤φlt;i+β

非连通型：φlt;i-β

二维空间一个重要优点是星座的构型在二维空间中可以用简单的几何网格进行表示。对于常用的Walker-δ构型，其二维空间的表示如图4所示。设星座的构型参数为N/P/F，则其网格参数为

(1)

设首个轨道面首个卫星的坐标为(L(1,1),u(1,1))，则第m轨道面的第n颗卫星的坐标为

(2)

所有卫星在二维空间的运动可以分解为卫星沿轨道的运动和轨道面相对地球的转动，因此卫星坐标的导数为：

(3)

式中：ωs为卫星轨道运动的角速度，ωe为地球自转角速度。

2 二维图的数学模型

二维图的边界计算主要分为两部分，轨道经度边界(简称经度边界)和相位边界。求解经度边界主要是求解轨道面与覆盖圆相切的问题，求解相位边界主要是求解轨道面与覆盖圆相交的问题。

2.1经度边界数学模型

在经度边界，轨道面与覆盖圆相切。设目标点经纬度为(λc,φc)，当φc-β≤i≤φc+β时，有两个轨道面与覆盖圆相切。设此时的轨道经度分别为Lb1，Lb2，切点的相位分别为u1，u2，对应的轨道面与赤道面的交点为A1，A2，如图5(a)所示。根据球面几何，有：

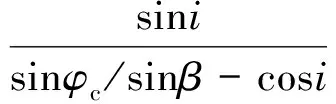
(4)

如果ξlt;0，则ξ=ξ+π。同时还有：

(5)

l=arcsin(sinβ/sinξ)

(6)

设α=i+ξ，b1为C和A1之间的经度差，则有

(7)

b2=π-b1

(8)

则二维图的经度边界为：

(9)

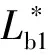
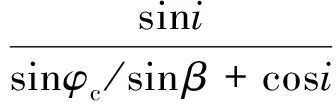
(10)

α*=i-ξ

(11)

2.2相位边界数学模型

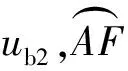
(12)

可以推导出：

(13)

和

l2=arctan(tanβcosδ)

(14)

如果b=0，则有

(15)

如果b≠0，则有

(16)

则对应的相位边界为

(17)

3 二维图的基本性质及其覆盖条件分析

3.1二维图的基本性质

对二维空间的坐标进行调整之后，可以得到二维图边界的解析数学模型，从而可以对二维图的基本性质进行分析研究。而基于二维图的星座构型设计方法则正是建立在二维图的基本性质和连续覆盖条件基础之上。通过研究分析，可以得到以下结论：

性质1. 单个卫星对单个目标点的覆盖二维图为中心对称图形，设目标点经度为λc，则其对称中心的坐标为(λc-π/2,π/2)。

性质2.x轴为升交点赤经时的二维图可以看做x轴为轨道经度时的二维图的切变变换，变换矩阵为：

(18)

式中：ω=ωe/ωs。

性质3.x轴为升交点赤经时的二维图也是中心对称图形，设目标点经度为λc，则其对称中心的坐标为(λc-π(1-ω)/2,π/2)。

性质4. 对于i≤φc+β的情况，当覆盖圆半径缩小到0时，二维图将缩小成两个关于中心点对称的极点。其中一个极点的坐标为

(19)

性质5. 对于非连通二维图，当目标点位于赤道上时，其每个半图都是中心对称图形，其对称中心为各自的极点。

以上性质可以由球面几何的相关知识得到证明，由于篇幅的限制，这里证明过程不再赘述。

3.2二维图的四重连续覆盖条件

由二维图的定义可知，当卫星进入目标点的二维图时，卫星能够实现对目标点的覆盖。对于纬度相同而经度不同的目标点，其二维图是沿经度平移的关系，同一卫星对这些点的覆盖位置也是平移的关系。对于同一纬度上的随机点，其二维图的平移量是随机的。当将这些随机的二维图看做是重合且固定时，则卫星的相对位置需要增加一个沿经度的随机量。虽然星座中卫星的轨道可能为回归轨道或者同星下点轨道，其运动轨迹可能是固定的，但增加沿经度的随机量后，其运动轨迹则变为随机的。因此当星座网格能在随机移动条件下对某个二维图进行连续覆盖时，该星座在实际运动中可以实现对整个纬度带的连续覆盖。同样，任意移动条件下能够实现对某个二维图四重连续覆盖的星座网格，也能实现对该纬度带的四重连续覆盖。这是连续覆盖条件的研究思路。

如果由星座网格中任意三个卫星组成的三角形中不包含有其他更小的三角形，则定义该三角形为星座网格的一个单位三角形。同样的方法也适用于单位平行四边形概念的定义。由于单重连续覆盖条件是多重连续覆盖条件的基础，因此，首先提出单重连续覆盖条件如下：

当连通凸型二维图包含有星座网格的任一单位三角形时，在任意移动条件下，该星座网格可以实现对该二维图的单重连续覆盖。

通过对单重连续覆盖条件的扩展，可以进一步得到四重连续覆盖条件。对于连通凸型二维图来说，其四重连续覆盖的必要非充分条件为(见图7)：

条件1：当连通凸型二维图可以包含如图7(a)所示的四个两两相邻的单位平行四边形所组成的复合平行四边形或如图7(c)所示的由四个依次相邻的单位平行四边形所组成的复合平行四边形时，在任意时刻至少有一个单位平行四边形完全处于二维图内，即二维图在任意时刻至少可以包含四个星座网格顶点。

条件2：对于满足条件1的星座网格，任意改变其相邻轨道卫星之间的相位差而形成的新的网格，仍能满足在任意时刻至少有四个顶点在二维图内(如图7(b)和图7(d)所示)。

以上的条件可以用初等几何知识进行证明，这里不再赘述。同样用初等几何知识，将以上结论进行扩展，即当连通凸型二维图可以包含由四个单位平行四边形组合形成的任意图形时，该单位平行四边形所组成的星座网格及其相位变化网格，都能满足连续四重覆盖的条件。但是以上两种组合情况对应的星座网格较为简单直观，便于星座构型的设计，可以作为星座设计的基础。

对于连通凹型和非连通型二维图，可以将下半图绕对称中心旋转180°，使下半图和上半图完全重合，而星座网格对下半图的覆盖则可以等效为一个与原网格运动方法完全相反的虚拟网格对上半图的覆盖。原星座网格和虚拟星座网格将会产生四类重合点，设其分别为“①”“②”“③”“④”，如图8所示。如果二维图的半图包含一个某类重合点，星座网格运动到该类重合点附近时至少有两个顶点包含于二维图内。因此当二维图的半图包含的每类重合点不少于两个时，星座网格在该二维图内至少有4个顶点。在重合点的统计过程中，需要注意的是，对于连通凹型二维图，中心对称点必然是其中一个重合点，但考虑到中心对称点可同时包含进两个半图中去，因此中心对称点及其经度上的重合点都应看做是半个重合点。同时，对于首尾相连的二维图，其经度边界上的重合点也应该看做是半个重合点。

4 四重覆盖星座构型设计方法研究

4.1星座构型初步设计

对于单位平行四边形的第1种组合，如图9所示，设连通凸型二维图的经度宽度LW=Lb1-Lb2，其中Lb1和Lb2分别为其经度边界，则星座轨道面个数P需满足：

2π/Plt;LW/2

(20)

则有

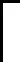
(21)

运用第3.2节模型，计算中心对称点前后一个经度网格的相位边界点，分别为A，B，C，D，且其相位跨度为uH=uA-uB，则星座每个轨道面的卫星数S满足：

2π/Slt;uH/2

(22)

则有

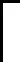
(23)

相应的F的取值范围为F=0,1,…,P-1。

同样，对于平行四边形的第2种组合，轨道面个数P需满足：

2π/Plt;LW/4

(24)

因此

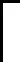
(25)

每个轨道面的卫星数S满足：

2π/Slt;uH

(26)

因此

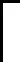
(27)

F的取值范围为F=0,1,…,P-1。

当P较小时，构型不能满足第2种情况的条件，此时以第1种情况的结果为主。当P较大时，第2种情况的结果往往比第1种情况的设计结果更优，所需要的卫星数量更少。因此在星座设计时，需要对于两种情况的结果进行综合，得到较优的构型结果。

4.2星座构型的二次筛选

对于i≤φ≤i+β的整个纬度带地区，用球面几何可以证明，高纬度的二维图可以完全包含于低纬度的二维图内。二维图随着纬度的变化关系如图10所示。能够包含于高纬度二维图的复合平行四边形也可以包含于低纬度的二维图，即可以满足高纬度地区四重连续覆盖的星座也可以满足低纬度地区的连续覆盖。所以在星座设计时，只需要以最高纬度点的二维图为基础进行星座设计，所得到的星座构型可以满足i≤φ≤i+β整个纬度带的四重连续覆盖要求。

对于φlt;i的纬度带地区，由于其二维图为非凸型，直接进行星座网格设计比较复杂。为了简化设计过程，可以在以连通凸型二维图为基础设计的星座构型基础上，采用纬度带验证法。具体方法就是将φlt;i地区划分为多条微小的单元纬度带，以每条单元纬度带中心纬度作为该纬度带的纬度进行连续覆盖验证，从而对以上设计结果进行二次选择。如果某一构型能够实现对所有单元纬度带的四重连续覆盖，则该构型能够实现对整个区域的四重连续覆盖。图11为星座设计的整个流程图。

对于低纬度的非连通型二维图，其覆盖情况比较复杂，很难用解析的方法直接进行构型设计。虽然需要采用划分纬度条带的方法依次对构型进行筛选，但覆盖的情况则可用二维图解析模型和连续覆盖条件直接进行判断，而不需要仿真整个覆盖过程，因此属于半解析的方法，相比于采用各种进化算法并需要不断进行覆盖仿真的现代设计方法，减小了计算量和计算时间。

5 仿真分析

仿真1.设计能够实现全球连续四重覆盖的卫星星座构型。其中卫星轨道为圆轨道，高度为20200 km，轨道倾角为55°，星载设备的信号最小可见角为5°。

采用基于二维图的星座设计方法，对星座构型进行设计与筛选。基于四重覆盖条件中两种单位平行四边形的组合方式，设计结果如表1所示。

从表1可以看出，当P值较小时，星座构型不满足组合2的条件，设计结果以组合1的结果为主；当P增大时，组合2所对应的结果所需要的卫星数量明显少于组合1的结果所需要的卫星数量。同时还可以看出，当P≥3时，组合1对应的结果中S的值都为6；当P≥5时，组合2对应的结果中S的值都为3。这是因为当纬度为90°时，目标点的二维图为首尾相连近乎矩形的条状凸型(见图12)，对应的最小相位宽度为133.527°。根据式(23)可知组合1对应的最小的S值为6，根据式(27)可知组合2对应的最小S值为3。

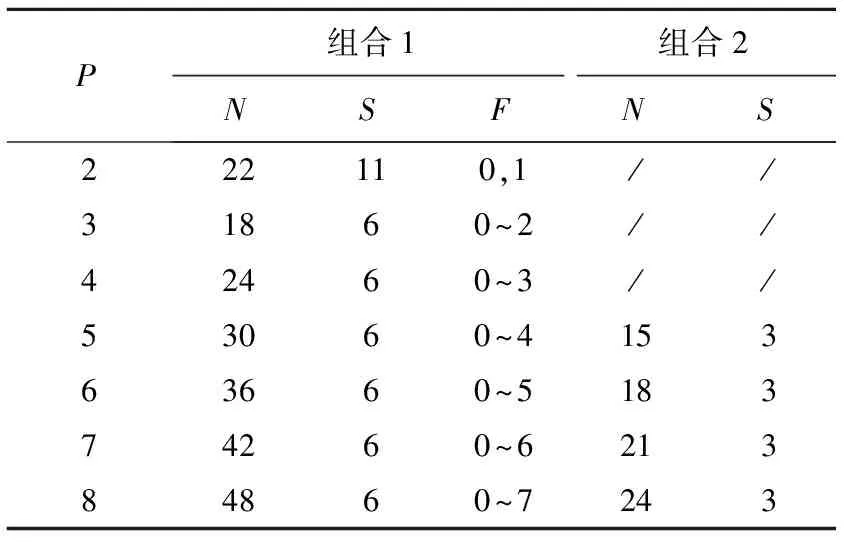
表1 两种组合方式对应的设计结果Table 1 The results of the two compound modes

结合STK软件对两种组合对应的构型结果进行仿真分析，并以我国陆地为覆盖区域，将各种构型的平均几何精度因子(Geometric dilution of precision,GDOP)值进行比较，如图13所示。从图13可以看出，组合2的结果所需卫星数少于组合1的结果，而组合1的结果平均GDOP值小于组合2的结果。

仿真2. 在仿真1的基础上，分析15/3/2构型的覆盖情况。

从表1可以看出，15/3/2不在可以满足全球四重连续覆盖的构型之列。从第4.2节的覆盖条件4可以看出，15/3/2能够满足连通凸型二维图的连续四重覆盖，即该构型能够满足纬度55°以上地区的连续四重覆盖。将纬度55°以下地区进行微小纬度带的划分，并逐条验证其覆盖情况。以bool型变量Y表示其是否能满足对当前纬度带的连续四重覆盖，通过不断细化纬度带，得到如表2所示结果。

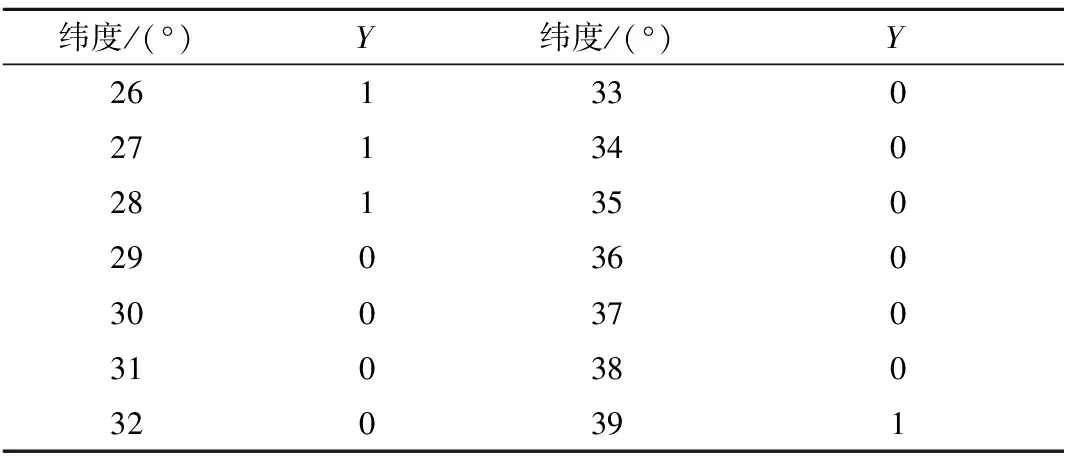
表2 15/3/2构型对纬度带的覆盖情况Table 2 Coverage performance of the configuration 15/3/2 for the latitude belts

从表2可以看出，该星座构型不能实现对纬度区间30°～38°的四重连续覆盖。采用STK软件对该星座构型的覆盖情况进行校验，结果如图14所示。从图14可以看出，分析结果与实际验证情况较为吻合。

6 结 论

基于二维图的星座构型设计是星座构型设计中的新方法，还需要更加深入与广泛的研究与发展。通过对二维空间的坐标系的调整，利用球面几何的方法建立了二维图的解析几何模型，同时对二维图的基本几何性质进行了深入研究，从而完善二维图理论，扩展二维图在星座构型设计上的应用与发展。创造性地将星座对纬度带的连续覆盖转化为对纬度带上任一点二维图的连续覆盖，分析了星座网格的四重连续覆盖条件。在此基础上，采用直接设计和验证筛选两种思路，提出了四重覆盖星座构型的设计方法，避开了复杂的覆盖性能统计过程。最后通过实例仿真，说明了模型的正确性，以及星座构型设计方法的有效性。

[1] Walker J G, Continuous whole-Earth coverage by circular-orbit satellite patterns[R]. Farnborough, Hants: Royal Aircraft Establishment, March 1977.

[2] Lang T J. Optimal low Earth orbit constellations for continuous global coverage[C]. Astrodynamic Specialist Conference, Victoria, Canada, August 16-19, 1993.

[3] Lang T J. Low Earth orbit satellite constellations for continuous coverage of the mid-latitudes[C]. Astrodynamic Specialist Conference, San Diego, USA, July 29-31, 1996.

[4] 宋志明, 戴光明, 王茂才, 等. Walker星座区域覆盖理论分析[J]. 计算机工程与设计, 2014, 35(10): 3639-3644.[Song Zhi-ming, Dai Guang-ming, Wang Mao-cai, et al. Theoretical analysis of Walker constellation coverage to area target[J]. Computer Engineering and Design, 2014, 35(10): 3639-3644.]

[5] 韦娟, 张润. 对地侦察卫星星座优化设计及仿真分析[J]. 西安电子科技大学学报, 2013, 40(2): 138-147.[Wei Juan, Zhang Run. Optimization design and simulation analysis of Earth reconnaissance satellite constellation[J]. Journal of Xidian University, 2013, 40(2): 138-147.]

[6] 宋丹, 许承东, 胡春生, 等. 基于遗传算法的多星座选星方法[J]. 宇航学报, 2015, 36(3): 300-308.[Song Dan, Xu Cheng-dong, Hu Chun-sheng, et al. Satellite selection with genetic algorithm under multi-constellation[J]. Journal of Astronautics, 2015, 36(3): 300-308.]

[7] 王励, 王炎娟, 张辉, 等. 基于NSGA-Ⅱ算法的区域覆盖卫星星座优化[J]. 计算机仿真, 2009, 26(4): 80-84.[Wang Li, Wang Yan-juan, Zhang Hui, et al. Optimization of regional coverage reconnaissance satellite constellations by NSGA-Ⅱ algorithm[J]. Computer Simulation, 2009, 26(4): 80-84.]

[8] 邓勇, 王春明, 胡晓惠. 基于空间纬度区域优化的红外近地轨道星座设计[J]. 宇航学报, 2010, 31(5): 1368-1373.[Deng Yong, Wang Chun-ming, Hu Xiao-hui. A spatical latitudinal region optimization-based infrared LEO constellation deign[J]. Journal of Astronautics, 2010, 31(5): 1368-1373.]

[9] John M H, Maria J E, Ronald E T, et al. Design good partial coverage satellite constellations[J]. Journal of Astronautical Sciences, 1992, 20(1): 215-239.

[10] Ulybyshev S Y. Satellite constellation design for complex coverage[J]. Journal of Spacecraft and Rockets, 2008, 45(4):843-839.

[11] Ulybyshev S Y. Design of satellite constellations with continuous coverage on elliptic orbits of molniya type[J]. Cosmic Research, 2009, 47(4): 310-321.

[12] Ulybyshev S Y. Geometric analysis and design method for discontinuous coverage satellite constellations[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(2): 549-557.

[13] Ulybyshev S Y. General analysis method for discontinuous coverage satellite constellations[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(2): 2475-2482.

[14] 李勇军, 赵尚弘, 吴继礼. 一种低轨卫星星座覆盖性能通用评价准则[J]. 宇航学报, 2014, 35(4): 410-417.[Li Yong-jun, Zhao Shang-hong, Wu Ji-li. A general evaluation criterion for coverage performance of LEO constellations[J]. Journal of Astronautics, 2014, 35(4): 410-417.]

[15] 陈晓宇, 戴光明, 陈良, 等. 一种基于球面剖分的星座性能分析方法[J]. 宇航学报, 2016, 37(10): 1246-1254.[Chen Xiao-yu, Dai Guang-ming, Chen Liang, et al. A method for constellation performance analysis based on spherical subdivision[J]. Journal of Astronautics, 2016, 37(10): 1246-1254.]

AConstellationDesignMethodforQuadrupleContinuousEarthCoverage

MENG Shao-fei1, LIU Xin-xue1, YANG Qi1, ZHU Tao2

(1.Rocket Force University of Engineering, Xi’an 710025, China; 2. Xi’an Surveying and Mapping Technological Center, Xi’an 710054, China)

Aiming at the intricate coverage models and inconvenient coverage statistics, a new design method for a quadruple continuous coverage constellation is proposed based on the two-dimensional maps. The preceding two-dimensional space coordinate system is improved and the analytic models of the two-dimensional maps are built via the analysis of the relative positions between the coverage circles and satellite orbits using the spherical geometric knowledge. The models are further studied and the geometric properties of the two-dimensional maps are concluded. By conversion from the continuous coverage of the latitude belt to the continuous coverage of one two-dimensional map in the belt, the single and quadruple continuous coverage conditions are put forward. On this basis, the design and screening methods of the constellation configuration for quadruple continuous coverage are integrated to avoid the complex statistics process of the coverage performance. Finally, the simulation for the two-dimensional theory and constellation design method suggests the feasibility of the new method.

Constellation configuration; Spherical geometry; Two-dimensional maps; Quadruple continuous coverage

V448

A

1000-1328(2017)11- 1160- 08

10.3873/j.issn.1000- 1328.2017.11.004

2017- 03- 06;

2017- 09- 04

孟少飞(1989-)，男，博士生，主要从事飞行动力学与制导，卫星星座构型设计等方面的研究。

通信地址：陕西省西安市灞桥区同心路2号(710025)

电话：13572098502

E-mail: shaofei_m@sina.com