一种面向固定配平型弹头的螺旋机动控制方法
周 敏,周 军,卢明飞
(1. 西北工业大学精确制导与控制研究所,西安 710072;2. 西安应用光学研究所,西安 710065)
一种面向固定配平型弹头的螺旋机动控制方法
周 敏1,周 军1,卢明飞2
(1. 西北工业大学精确制导与控制研究所,西安 710072;2. 西安应用光学研究所,西安 710065)
针对固定配平型弹头过载方向可控但过载大小不可控因而无法同时实现螺旋机动所需纵向/侧向过载的问题,提出一种适用于固定配平型弹头单通道变质心滚转控制模式的螺旋机动控制方法。首先,建立了可直观描述螺旋锥角、螺旋角速度等螺旋机动运动特性的弹目相对运动关系方程。然后,基于螺旋锥角、螺旋运动角速度等螺旋运动状态与弹目视线角速率关系,合理设计螺旋机动指令,保证螺旋机动末端弹目视线角速度收敛到零。最后,采用反演法实现弹头质点运动与滚转姿态运动的制导控制一体化设计,通过一维变质心控制滚转姿态调整法向过载方向,使得过载分量能够控制弹头速度矢量与视线的夹角跟踪设计的螺旋运动锥角指令,而剩余过载分量产生大小不可控但旋转方向不变的螺旋运动角速度,实现螺旋机动弹道的运动特性。数学仿真表明,本文提出的螺旋机动控制方法可实现滚转单通道控制固定配平型弹头的螺旋机动,设计思路直观简单,便于工程应用。
固定配平型弹头;螺旋机动;制导控制一体化;反演控制
0 引 言
再入弹头机动飞行可有效规避防御系统拦截,提高其生存能力。三种常用的机动弹头气动外形有“+”型气动舵外形、攻角可控倾斜转弯外形和固定配平外形。相比于“+”型气动舵的三轴控制模式、攻角可控倾斜转弯的两轴控制模式,固定配平型弹头通过最简单的滚转单通道控制即可实现再入机动飞行[1-3]。采用置于弹头内部的一维变质心控制系统具有保持良好气动外形、无舵面烧蚀、控制效率高等优点,对于实现固定配平型再入弹头滚转单通道控制具有传统气动舵、直接力等控制手段无法比拟的优势[2,4-5]。
美国的MK500机动再入体是固定配平型弹头的典型代表,采用弯头锥的不对称气动外形产生非零配平攻角,利用一维变质心方式进行滚动控制从而实现程序飞行[2,6]。固定配平型弹头利用不对称的气动外形设计或质量配置产生非零配平攻角,俯仰/偏航运动静稳定,可不施加主动控制,依靠弹头自身静稳定性自动收敛到非零配平攻角和零侧滑角,在此过程中,弹头过载大小无法主动控制。但利用变质心控制速度倾侧角大小,可实现过载方向调节。因此,固定配平型弹头具有过载大小不可控仅方向可控的特点。
针对滚转单通道控制模式下固定配平型变质心弹头过载大小不可控仅方向可控的特点,国内外诸多学者对其动力学特性、轨迹规划及制导控制方法进行了研究。文献[7]对一维变质心控制的固定配平型飞行器非线性动力学特性进行了分析。文献[8]将直接配点法应用于固定配平型飞行器的飞行弹道优化中。Gracey等[1]研究通过合理滚转运动消耗多余升力提高固定配平型飞行器落点精度的方法。文献[2]进一步引入了虚拟目标信息,解决了考虑终端角度约束的固定配平型飞行器制导律设计问题。文献[6]提出了一种滚转制导律与三维圆周制导律结合的新方法,并成功应用于具有终端角度约束的固定配平型再入弹头末制导。然而,固定配平外形作为再入机动飞行器最简单的布局形式,实现其机动突防弹道设计与制导控制具有重要意义,以上文献均未涉及此类弹头机动突防方法的相关研究。
螺旋机动是一种具有较好突防效果的[9]典型机动弹道形式。然而,已有螺旋机动控制方法已不再适用于滚转单通道控制模式下过载大小不可控仅过载方向可控的固定配平型变质心弹头的螺旋机动控制。已有的螺旋机动控制方法需分别设计并跟踪纵向、侧向机动过载指令,如宋贵宝通过视线高低角速率和方位角速度的正弦变化[10],林鹏利用二维变质心跟踪纵向、侧向过载指令,实现螺旋机动[11]。而固定配平型弹头在滚转单通道控制模式下仅能实现过载方向调节,无法同时满足纵向和侧向过载需求,需要研究适用于固定配平型弹头单通道控制模式的螺旋机动控制方法。
本文针对固定配平型变质心弹头滚转单通道控制模式下过载大小不可控仅方向可控的特点,建立可直观描述螺旋运动特性的弹目相对运动方程,合理设计螺旋机动指令,采用反演法[12]实现弹头质点运动与滚转姿态运动的制导控制一体化设计。通过调整速度倾侧角控制过载方向,实现期望螺旋锥角指令跟踪,并利用剩余过载产生方向不变大小不控的螺旋运动角速度,从而实现螺旋机动飞行,有效提高固定配平型弹头的机动突防能力。
1 模型描述
1.1弹头动力学模型
固定配平型变质心弹头利用一维变质心方式实现滚转单通道控制,本节建立弹头质点运动与滚转姿态运动四自由度模型,引入以下假设:
(1) 假设大地为平面,忽略地球自转引起的惯性力干扰;
(2) 假设弹头俯仰、偏航通道可实现瞬时配平,即ωy≡0,ωz≡0;
(3) 假设弹头的配平攻角和侧滑角为小量,即满足cosα≐1,cosβ≐1,sinα≐0,sinβ≐0;
(4) 假设弹头质量分布满足理想轴对称特点,惯量积满足Ixy≐0,Ixz≐0,Iyz≐0;
(5) 假设初始时刻一维变质心机构的质心位置与弹头质心位置重合;
(6) 假设一维变质心可动部分的惯量很小,控制过程中可动质量块移动下的系统总惯量不变;
(7) 假设变质心可动质量块的移动速度、加速度影响很小,忽略相应的惯性力和惯性力矩干扰。
基于以上假设建立的固定配平型变质心弹头质点三自由度运动数学模型[1]为
(1)
(2)
(3)
(4)
(5)
(6)
式中:V、θ、ψV分别为飞行速度、弹道倾角和弹道偏角;x、z、h分别为飞行器地面位置坐标和飞行高度;D和L分别为气动阻力和升力;m为系统总质量;γV为速度倾侧角;g为重力加速度,平面大地假设下取常值9.8 m/s2。
固定配平型变质心弹头滚转运动数学模型[3]为
(7)
(8)
式中:ωx为弹头的滚转角速度;μA为一维变质心可动质量块相对于系统总质量的质量比;Mx为弹头受到的滚转气动力矩;Ix为弹头绕纵轴的转动惯量;zm为一维变质心的控制量,即一维变质心可动质量块的质心相对于弹头质心z向位移。根据假设条件(5)可知其初始值为zm(0)=0。
1.2弹目相对运动关系模型
固定配平型变质心弹头利用一维变质心方式实现滚转控制,从而改变过载方向实现螺旋机动,因此建立的弹目相对关系方程应能够直观描述螺旋运动状态;契合固定配平型弹头滚转单通道控制的特点。鉴于此,引入以下定义:
(1) 误差角η:定义弹头速度矢量V与弹目视线矢量l的夹角为误差角,这一角度描述螺旋运动锥角的大小;
(2) 误差角平面:定义弹头速度矢量V与弹目视线矢量l张成的平面为误差平面,这一平面为本文描述螺旋运动的旋转平面,如图1阴影所示;
(3) 误差坐标系Mxηyηzη:定义坐标系原点为弹头质心M,Mxη轴与弹头速度矢量V重合,Myη轴垂直于速度矢量V且在误差平面内,Mzη轴与Mxη轴、Myη轴构成右手坐标系。
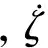
弹目视线矢量l满足[13]
(9)
式中:δηl/δηt为弹目视线矢量l在误差坐标系中的相对导数,ωη为误差坐标系的绝对转动角速度矢量。为了直观描述螺旋运动特性,结合式(1)~(6),忽略重力作用,在误差坐标系中展开式(9),整理得到弹目相对运动关系方程为
(10)
(11)
(12)
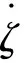
1.3螺旋机动指令设计
为了设计可行的螺旋机动指令,本节分析螺旋运动状态特征量η、ζ与视线角速度的关系。
首先,明确视线坐标系Mxsyszs的定义:坐标系原点与弹头质心M固连,Mxs轴与弹目视线重合指向目标为正,Mys轴在铅垂平面内与视线垂直指向上为正,Mzs轴与Mxs轴、Mys轴构成右手坐标系。
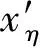
V=V(cosη·i-cosζsinη·j+sinζsinη·k)
(13)
式中:i,j,k分别为视线坐标系Mxsyszs的Mxs、Mys以及Mzs各轴的单位矢量。
同理,弹目视线矢量l满足[13]
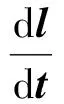
(14)
式中:δsl/δst为弹目视线矢量l在视线坐标系中的相对导数,ωs为视线坐标系的绝对转动角速度矢量,在视线坐标系中表示为
(15)
其中,λD为视线高低角,是视线矢量l与水平面的夹角;λT为视线方位角,是视线矢量l在水平面投影与地面惯性系基准x方向的夹角。结合式(13)、(15),在视线坐标系中展开式(14),整理得到视线角速度满足
(16)
(17)
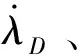
考虑固定配平型变质心弹头滚转单通道控制下过载大小不可控仅方向可控的特点,提出适用于固定配平型弹头的螺旋机动控制方案:控制螺旋运动锥角的大小,螺旋运动角速度的大小不控,但通过控制滚转运动方向保证螺旋运动的旋转角速度不变号。因此,设计连续且一阶可导的螺旋机动指令为
(18)
式中:ηm为配平型变质心弹头螺旋机动时的常值螺旋锥角大小;lm为弹头结束以常值螺旋锥角ηm螺旋运动时的弹目相对距离。
图3为固定配平型变质心弹头需跟踪的螺旋锥角指令示意图,当l≥lm时固定配平型变质心弹头以固定螺旋锥角进行螺旋机动;llt;lm时,弹头螺旋锥角逐渐减小到零。
基于视线角速度方程(16)~(17)设计制导律时,为了保证制导末端落点精度较高,总是要求视线高低角速度、视线方位角速度满足以下方程
(19)
本文设计的螺旋制导指令(18)可保证式(19)成立,从而实现螺旋机动的前提下可保证末端制导精度。证明如下。
基于洛必达法则对式(16)求极限得到
(20)
对式(18)求导为
(21)
2 螺旋机动制导控制一体化设计
2.1面向控制的一体化制导控制模型
针对固定配平型变质心弹头滚转单通道控制的特点,设计螺旋机动指令如式(18),仅控制螺旋锥角大小,而螺旋运动角速度大小不控,固定配平型变质心弹头的螺旋机动模型为
(22)
其中,固定配平型变质心弹头的滚转运动状态变量速度倾侧角γV是隐含的,因此,实现螺旋机动的制导控制一体化需要对滚转姿态回路的状态变量进行转换,选取滚转单通道的姿态角运动状态为
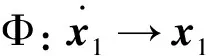
(23)
其中
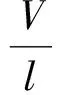
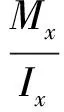
得到面向控制的固定配平型变质心弹头制导控制一体化模型为如式(23)所示的非线性系统。控制输入为一维变质心可动质量块的位移zm,满足块严格反馈形式,可以基于反演法来设计控制系统。
2.2基于反演法的制导控制一体化设计
本节采用反演法为固定配平型变质心弹头设计螺旋机动控制器,使得制导控制一体化系统输出跟踪螺旋机动指令。具体设计流程如图4所示,基于建立的弹头螺旋机动模型如(22)式,按照3个步骤设计动态面,引入指数趋近律,分别实现螺旋锥角ηC、速度倾侧角γV和滚转角速度ωx的跟踪。具体设计过程阐述如下。
步骤1. 定义动态面
s0=x0-ηC
(24)
按照非线性反馈设计动态面s0变化率为
(25)
式中:αgt;0,kgt;0。对式(24)求导并结合式(23)得到第一层的虚拟控制量x11d为
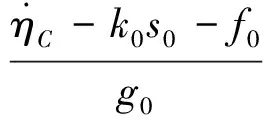
(26)
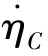
步骤2. 定义动态面
(27)
其中,结合步骤1得到的虚拟控制量x11d,确定的虚拟控制量x1d为
(28)
按照指数趋近律选取动态面s1的变化率为
(29)
对式(27)求导并代入式(29)、式(23)得到
(30)
因此,得到第二层虚拟控制量为
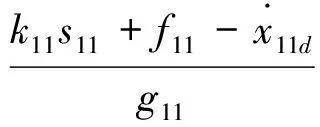
(31)
(32)
其中,τ1为一阶滤波器的时间常数,在此,记一阶滤波器的跟踪误差为ε1=x11v-x11d。
步骤3. 定义动态面
s2=x2-x2d
(33)
按照指数趋近律选取动态面s2的变化率为
(34)
对式(33)求导并引入式(23)得到质量块位移指令即控制量为
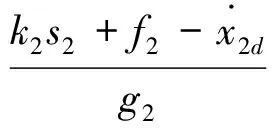
(35)
(36)
其中,τ2为一阶滤波器的时间常数,记该一阶滤波器的跟踪误差为ε2=x2v-x2d。
对闭环系统的稳定性进行分析,选取Lyapunov函数为
(37)
对式(37)求导并将式(25)、(29)、(34)代入得到
(38)
由式(32)、(36)可知
(39)
(40)
另外,引入参数λ满足
(41)
并选取合适的滤波器参数0lt;τ1lt;2、 0lt;τ2lt;2,使得λgt;0成立。将式(40)、(41)代入式(38)得到
(42)
(43)
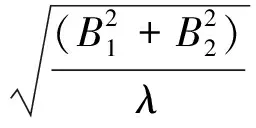
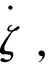
3 仿真校验
本文提出的螺旋机动控制方法适用于过载大小不可控而方向可控的固定配平型变弹头。为了验证这一螺旋机动控制新方法,以某型固定配平型的一维变质心滚转控制弹头为例,对质心运动及滚转姿态运动进行四自由度数学仿真。
仿真中,假设弹头俯仰运动和侧滑运动均可实现瞬时配平,即瞬时稳定在配平攻角和零侧滑角状态。飞行器从28 km高度开始进行螺旋机动飞行,初始弹道倾角为-13.7°,初始弹道偏角为-1.1°,螺旋锥角指令参数ηm=8°、lm=2 km。另外,假设弹头的一维变质心机构为考虑位移限幅的二阶动态环节,其自然频率ωn=50 rad/s、阻尼为ξ=0.7,变质心机构可动部分的位移限幅为|zm|≤1 m。,得到的仿真曲线如图5 ~10所示。
图5给出了弹头运动的纵向位移x、侧向位移z和高度h三维飞行轨迹,具有螺旋运动特性,且落点精度较高,偏差约为2.5 m。
如图6所示,固定配平型变质心弹头可以较好的跟踪期望的螺旋锥角;速度倾侧角也可较好地跟踪速度倾侧角指令(见图7)。
图8为螺旋机动过程中的螺旋运动角速度曲线,本文实现了保持为正的螺旋运动角速度。另外,在飞行末段螺旋锥角接近零时速度与弹目视线近似重合,误差平面退化为直线,此时的螺旋运动角速度没有实际物理意义。
如图9所示,在恒定螺旋锥角的螺旋机动过程中,弹头飞行速度矢量的指向近似为圆心固定的圆周运动,弹道倾角和弹道偏角以周期性的往复运动规律变化,当螺旋锥角逐渐减小时,弹道倾角和弹道偏角振荡幅值逐渐减小。另外,图10为实现螺旋机动过程中弹头内部一维变质心机构的位移变化曲线,不难发现,机构位移在初始振荡后基本不变,为弹头滚转运动提供所需滚转控制力矩。
以上仿真结果表明,本文提出的螺旋机动控制方法可实现固定配平型变质心弹头的螺旋机动弹道,在末段零螺旋锥角时以较高精度实现期望落点。
4 结 论
本文针对固定配平型变质心弹头过载大小不可控仅方向可控的特点,在误差坐标系中建立了弹目相对运动关系模型,得到了螺旋运动锥角以及螺旋运动角速度的方程,相比于常用的弹目视线角速率方程可实现对螺旋运动特性的直观描述。针对固定配平型弹头滚转单通道控制的限制,提出一种新的螺旋机动控制方法。通过合理设计保证末端视线角速率收敛到零的螺旋锥角指令,采用反演法实现了弹头质点与滚转姿态运动四自由度系统的制导控制一体化设计,通过控制弹头滚转运动改变速度倾侧角大小,基于大小不可控的总过载产生期望螺旋锥角指令跟踪所需的过载分量,而剩余过载作用则产生方向不变大小不控的螺旋运动角速度,从而实现螺旋弹道的运动特性。数学仿真表明,本文提出的螺旋机动控制方法可以实现固定配平型变质心弹头的螺旋机动,在保证较高落点精度的同时有效提高了弹头的突防能力。
[1] Gracey C, Cliff E M, Lutze F H, et al. Fixed-trim re-entry guidance analysis [J]. Journal of Guidance Control and Dynamics, 1982, 5(6): 558-563.
[2] 耿克达, 周军, 林鹏. 带落角约束的固定配平攻角飞行器滚转制导律设计[J]. 固体火箭技术, 2015, 38(3): 320-325. [Geng Ke-da, Zhou Jun, Lin Peng. Design of rolling-guidance law using virtual target with control of terminal azimuth for a fixed-trim vehicle [J]. Journal of Solid Rocket Technology, 2015, 38(3): 320-325.]
[3] Thomas P, Frank J R. Moving-mass roll control system for fixed-trim re-entry vehicle [J]. Journal of Spacecraft and Rockets, 1996, 33(1): 54-60.
[4] Wei P X, Gao C S, Jing W X. Roll control problem for the long-range maneuverable warhead [J]. Aircraft Engineering and Aerospace Technology, 2014, 86(5): 440-446.
[5] Li J Q, Gao C S, Jing W X, et al. Dynamic analysis and control of novel moving mass flight vehicle [J]. Acta Astronautica, 2017, 131: 36-44.
[6] 周军, 葛振振, 林鹏. 具有终端角度约束的固定配平型再入弹头制导方法[J]. 宇航学报, 2017, 38(4): 375-383. [Zhou Jun, Ge Zhen-zhen, Lin Peng. Terminal guidance law with impact angle constraint for the fixed-trim reentry warhead [J]. Journal of Astronautics, 2017, 38(4): 375-383.]
[7] Wang Y F, Yu J Q, Mei Y S, et al. Nonlinear dynamics of fixed-trim reentry vehicles with moving-mass roll control system [J]. Journal of Systems Engineering and Electronics, 2016, 27(6): 1249-1261.
[8] Robert T B, David S R. Trajectory optimization for a fixed-trim reentry vehicle using direct collocation and nonlinear programming [C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, USA, August 14-17, 2000.
[9] 顾文锦, 赵红超, 王凤莲. 反舰导弹末端机动的突防效果研究[J]. 宇航学报, 2005, 26(6): 758-761. [Gu Wen-jin, Zhao Hong-chao, Wang Feng-lian. Research on the penetration effect of terminal maneuver for anti-ship missile [J]. Journal of Astronautics, 2005, 26(6): 758-761.]
[10] 宋贵宝, 朱平云, 李红亮. 空舰导弹俯冲弹道螺旋机动制导律研究[J]. 兵工学报, 2014, 35(2): 220-225. [Song Gui-bao, Zhu Ping-yun, Li Hong-liang. Research on the guidance law for spiral maneuver of air-to-ship missile in dive trajectory phase [J]. Acta Armamentarii, 2014, 35(2): 220-225.]
[11] 林鹏, 周军, 周凤岐. 变质心再入飞行器螺旋机动指令设计及分析[J]. 西北工业大学学报, 2010, 28(4): 477-480. [Lin Peng, Zhou Jun, Zhou Feng-qi. Design and simulation of the helix maneuvering program for moving centroid reentry vehicle [J]. Journal of Northwestern Polytechnical University, 2010, 28(4): 477-480.]
[12] Shao X L, Wang H L. Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO[J]. ISA Transaction, 2015, 57: 10-22.
[13] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京:北京理工大学出版社, 2011: 36-37.
[14] Khalil H K. Nonlinear system [M]. Upper saddle river, New Jersey: Prentice-Hall, 2002.
[15] 赵暾, 王鹏, 刘鲁华,等. 带落角约束的高超声速飞行器一体化制导控制[J]. 控制理论与应用, 2015, 32(7): 925-933. [Zhao Tun, Wang Peng, Liu Lu-hua, et al. Integrated guidance and control with terminal angular constraint for hypersonic vehicles [J]. Control Theory and Applications. 2015, 32(7): 925-933.]
ASpiral-ManeuverControlMethodforaFixed-TrimWarhead
ZHOU Min1, ZHOU Jun1, LU Ming-fei2
(1. Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi’an 710072, China; 2. Xi’an Institute of Applied Optics, Xi’an 710065, China)
Given the problem that the common spiral-maneuver control method to realize both vertical and lateral overload needed is not applicable for a fixed-trim warhead with a controllable lift-force direction but an uncontrollable magnitude, a new spiral-maneuver control method is proposed for a moving-mass fixed-trim warhead in the control mode of single rolling channel. Firstly, the relative motion model is formulated with the spiraling angle and spiraling angular velocity. It is an intuitional description of the spiraling motion. Based on the relationship of the spiraling motion variables and angular rates of light-of-sight, the spiral-maneuver command is designed to ensure that the angular rates of light-of-sight converge to zero at the end. The back-stepping control method is then applied in the integrated guidance and control of the mass-point motion and the rolling attitude motion. The bank angle is controlled by a one-dimension moving mass to adjust the direction of the lift force. Thus, there’s a component of the lift force controlling the angle between the relative velocity vector and the line of sight to trace the desired spiraling angle, while the rest component results in a spiraling angular velocity with an invariable direction. Numerical simulations demonstrate that the proposed spiral-maneuver control method is effective for a fixed-trim warhead in the mode of single rolling channel control. It is simple and potential to be used in engineering.
Fixed-trim warhead; Spiral maneuver; Integrated guidance and control; Back-stepping control
V448.2
A
1000-1328(2017)11- 1195- 09
10.3873/j.issn.1000- 1328.2017.11.008
2017- 06- 12;
2017- 08- 29
中央高校基本科研业务费专项资金(3102017jg02004)
周敏(1987-),女,助理研究员,主要从事飞行器动力学、制导与控制方面的研究。
通信地址:陕西省西安市友谊西路127号234信箱(710072)
电话:(029)88492787
E-mail:zhoumin@nwpu.edu.cn

