空间物体椭圆轨道假设下碰撞通量计算与分析
周威萍, 沈 鸣, 高鹏骐, 郭效忠, 赵 有
(1. 中国科学院国家天文台, 北京 100012;2. 中国科学院大学, 北京 100049)
空间物体椭圆轨道假设下碰撞通量计算与分析
周威萍1,2, 沈 鸣1, 高鹏骐1, 郭效忠1, 赵 有1
(1. 中国科学院国家天文台, 北京 100012;2. 中国科学院大学, 北京 100049)
利用陈氏模型,不依赖于气体动理论和泊松统计假设,对近地空间物体环境中环绕飞行航天器碰撞通量的计算问题进行了研究。分析运行在椭圆轨道上的空间物体通过指定区域的4种情况,推导得到碰撞通量关于物体穿越统计区域所用时间的表达式。文章亦对圆轨道和椭圆轨道假设作了比较,并以铱星86为例,讨论了两种假设情况下空间物体对它的碰撞通量。结果显示,随着统计区域厚度的增加,椭圆轨道假设下的碰撞通量从约为圆轨道假设的4倍减小到1.4倍;圆轨道假设下,计入统计的空间物体数量随着统计区域的厚度变化产生的波动较大,椭圆轨道假设下的统计目标数量在区域厚度取5 km时可达圆轨道的60倍。
碰撞预警;碰撞通量;空间物体;航天器;卫星轨道
0 引 言
空间碎片的存在给人造卫星、空间站等航天器的安全运行带来了威胁,随着人类航天事业的发展,空间物体的数量在不断增加。航天器的撞击解体、空间碎片的二次解体更是加速了碎片的增长,给航天器的运行带来更具威胁的安全隐患[1-2]。为避免航天器因发生碰撞造成损失和空间灾难,须对航天器进行预警分析,对将与空间物体发生碰撞的航天器进行机动规避[3-4]。目前,是否发布航天器碰撞预警的衡量标准多为碰撞概率阈值,Foster等[5]对国际空间站(International space station, ISS)的碰撞规避机动进行了分析,结果表明:若ISS的碰撞概率大于10-4,则应该对其实施规避机动策略。阈值一般根据三个量来确定:风险降低率、机动次数、目标的先验碰撞风险。作为碰撞判定基准的先验碰撞风险理论上未知,可以用碰撞通量作为替代,碰撞通量根据背景空间物体的通量计算得到[6-7]。Kessler[8]在研究木星的八个卫星之间的碰撞概率时,提出了Cube Approach模型[9],该模型将空间分割成一个个小空间体积元,分别计算空间物体在这些体积元内的碰撞概率,相加得到这八个卫星之间的总碰撞概率。根据Cube Approach模型,这些空间体积元的尺寸相比空间物体的轨道不确定度足够小,当空间物体穿越其中时,物体的位置可以被认为是随机的,这种情况下,空间物体的运动与气体分子的运动相似,因而利用气体动理论模型计算空间物体之间的碰撞概率。Foster等[5]和Foster等[10]在确定航天器碰撞概率阈值的过程中,采用了Cube Approach模型计算空间物体对航天器的碰撞通量。为计算航天器在穿越空间物体云时的碰撞通量,NASA和ESA分别提出了ORDEM和MASTER模型[11-13],同样假设空间物体整体遵守气体动理论,分布上服从泊松统计。根据气体动理论,气体分子作直线运动且方向随机,它们的数密度是均匀的。然而,空间物体实际上遵循轨道运动规律,还受到地球引力摄动、日月引力摄动、大气阻尼摄动、太阳辐射压力摄动等因素的影响[14-15]。与气体分子不同,空间物体的数密度在纬度空间内并不均匀分布,它从赤道到碎片轨道所能到达的最大纬度不断增大,在碎片的最高纬度,其数密度比低纬度大几个数量级。基于这些因素,Chan[16]在1996年提出了不依赖于气体动理论模型和泊松统计假设的陈氏模型。
Dennis[17]假设空间物体的轨道为圆轨道,其升交点赤经在赤道平面上均匀分布,轨道平面的相位均匀分布,从而给出了空间物体数量的统计学分布。Chan[16]在此基础上对算法做了改进,给出了空间物体的数密度表达式,并结合两个物体之间的碰撞概率关系,得到不依赖于气体动理论模型和泊松统计假设的碰撞通量计算表达式,用以计算航天器在一段时间内与多个空间物体发生交会时,可能发生的碰撞风险。然而,空间物体的运行轨道实际上并不是绝对的圆,即使是偏心率为0.001的近圆轨道,也因为轨道的半长轴尺度而使得远、近地点的高度差量级为几十千米。大椭圆轨道的区别更加明显。在当前设备探测精度较高的情况下,这一差距相对较大,可能影响航天器的碰撞风险分析,从而降低碰撞预警的精度。此外,对于近圆轨道物体,即使它们的远地点和近地点高度相差较小,但由于作为统计区域的圆环厚度和高度不同,空间物体在该区域内的滞留时间(即有效统计时间)有可能远低于其轨道周期,从而导致该物体对航天器的碰撞概率远小于圆轨道假设下的结果。
文献[18]从数据分析的角度,利用陈氏模型,对国际空间站在一定统计区域厚度内来自空间物体的碰撞通量进行了计算分析,并与MASTER模型和ORDEM模型的结果进行对比。研究发现:随着统计区域厚度与标准差比值的变化,ISS的碰撞通量先增后减,椭圆轨道假设下碰撞通量计算结果的变化范围与ORDEM 3.0 模型以及MASTER模型的结果相接近;当比值为2时,碰撞通量的值与ORDEM 3.0模型的平均碰撞通量值相近;利用陈氏模型计算碰撞通量的方法在时间上明显优于其它模型。具体内容见参考文献[18]。本文从理论出发,给出了空间物体椭圆轨道假设下航天器碰撞通量计算理论的详细分析过程,以铱星86为例,计算了陈氏模型在圆轨道和椭圆轨道两种假设条件下航天器的碰撞通量,并将计算结果进行对比和分析。
1 圆轨道的碰撞通量
航天器的碰撞通量是指单位时间内,航天器与多个空间物体发生碰撞的概率总和。当航天器穿越多个空间物体时,航天器和空间物体各自有一个位置误差椭球与它们的位置误差相对应,由于空间物体靠近航天器的方向未知,可以假设它们的联合协方差各向同性,即误差椭球为球形。令该球体的联合协方差为σ2,则标准差为σ。
令航天器为主目标,对应的符号下标用1表示,其它空间物体为从目标,对应的符号下标用2表示。图1[16]描述了纬度θ上主、从目标的轨道,为便于说明,图中只给出了主目标作上升运动的情况;对应的,从目标可能作上升运动,也可能作下行运动。
为得到空间物体的数密度表达式,进而得到统计区域内空间物体对航天器的碰撞通量,将空间物体按轨道倾角进行分类,首先考虑ntotal个同类别的空间物体在赤道平面上的分布情况,然后考虑其在各自轨道平面内的统计分布,最后考虑一定厚度的高度空间,得到空间物体数密度关于统计区域厚度和轨道倾角的函数表达式。
两个物体之间的碰撞概率是交会距离的函数,根据空间物体的数密度可以得到单位时间内通过相遇平面的空间物体数量,乘以两个物体之间的碰撞概率表达式,再对时间积分即可得到航天器穿越某空间区域时的碰撞通量。
航天器穿越空间物体云时,受到的碰撞通量如下所示[16]:
(1)

2 椭圆轨道的碰撞通量
2.1空间物体通过统计区域的情况分析
图2给出了空间物体通过高度空间中某个统计区域时,其轨道相对该区域的位置关系。其中,两个实线圆所围起来的圆环区域为统计区域,圆环的内、外半径分别为r1和r2,椭圆轨道的近地点和远地点分别为d1和d2;虚线椭圆表示空间物体的运行轨道;A、B是空间物体轨道和圆环的交点。
圆轨道假设下航天器的碰撞通量计算理论中,近地空间物体的轨道“几乎为圆轨道”,它们的轨道完全处于厚度为h的统计区域内,如图2(a)所示。假设某个航天器的轨道半长轴为R1,则该统计区域圆环的内、外半径分别为r1=(R1-h/2),r2= (R1+h/2)。然而,空间物体的轨道并不一定完全被包含在所选定的某个统计区域中,根据空间物体的实际运动情况,可以将它们通过某个统计区域的状态分成以下四种情况:
1)若某空间物体的轨道近地点离地心的距离大于等于该统计区域圆环的内半径,且远地点离地心的距离小于等于圆环的外半径,则该空间物体的轨道完全包含在统计区域内。
2)根据图2(a)中对统计区域圆环内外半径的分析,当通过该区域的空间物体的偏心率小于等于[h/(2R1)]时,该物体的轨道才有可能完全处于统计区域内。然而,仅凭偏心率小这一条件并不能确定空间物体一定完全处在统计区域内。有些空间物体的近地点处于区域内,远地点在区域外,但仍然有很小的偏心率,如图2(b)所示。根据轨道运动规律,在这种情况下,空间物体有较长时间处在统计区域之外。
3)物体的近地点在区域外,远地点在区域内,如图2(c)所示。此种情况与情形2)类似,物体的近地点和远地点通常有且仅有一个处在统计区域内,另一个在区域外。不同的是,物体由于远地点在区域内部,使得其在统计区域内的滞留时间相对较长。但具有这种轨道的空间物体,其近地点轨道可能非常接近地球大气层,受地球大气阻力影响较大,导致其整个轨道运行周期减短,同时导致远地点高度下降,只有小部分轨道处在统计区域内,因而该空间物体滞留在统计区域内的时间相对轨道周期仍然很短。
4)物体的近地点和远地点都不在区域内,但轨道跨越了整个统计区域,如图2(d)所示。此时空间物体的近地点距地心的距离小于r1,远地点距地点的距离大于r2。这种情况下,空间物体的有效统计时间是其通过统计区域时,中间两部分轨道所花时间之和。
椭圆轨道假设下航天器的碰撞通量计算理论中,以空间物体在统计区域内的滞留时间率作为其对碰撞通量的贡献。所谓滞留时间率,是指对于某个空间物体,其代入计算的数量为该物体处在统计区域圆环内的时间与其轨道周期的比值,即将某空间物体在统计区域内滞留的时间记为Δt,轨道周期为T,则该物体的滞留时间率为Δt/T。图2(a)中,物体完全处于区域内,因而其数量统计值为1;图2(b)~2(d)情况下的空间物体都只有部分轨道位于区域内,因而这些物体的数量统计值应小于1。
2.1.1 平近点角与轨道高度的关系表达式
椭圆轨道上某点对应的时刻为物体的平均运动角速度与平近点角的函数:
M=n(t-τ)
(2)
式中:τ为物体过近地点的时刻。通过开普勒方程建立平近点角和高度之间的关系,根据高度得到平近点角,进而可根据式(2)得到物体在对应高度上的时刻。
空间物体的轨道方程为:
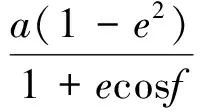
(3)
由真近点角f与偏近点角E的关系,结合开普勒方程
E-esinE=M
(4)
可得平近点角与轨道高度之间的关系,如下:
(5)
将式(5)代入式(2)得到椭圆轨道上的某点P与近地点之间的时间差如下:
(6)
根据式(3)可得对应于高度r的真近点角f的值,但由于计算中涉及除以偏心率e的运算,当偏心率较小时,如小于0.01,如果直接利用式(3)求cosf进而求真近点角f,容易造成结果的不稳定,所以采用下面的方法进行求解:
令
(7)
从而
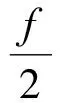
(8)
由于0≤f≤π,式(8)不为负,根据泰勒展开:
当0≤f≤π/2时,
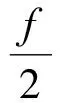
(9)
当π/2≤f≤π时,
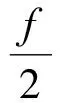
(10)
将式(9)或式(10)代入式(6)计算轨道上P点与近地点之间的时间差。
当偏心率较大时,可由式(3)直接计算真近点角f,代入式(6)得到轨道上P点与近地点之间的时间差。
2.1.2 空间物体统计数量的计算
两行轨道根数(Two line element, TLE)是北美防空司令部(North America aerospace defend command, NORAD)发布的在轨编目目标的轨道数据,它是目前最完备的地球轨道空间物体编目数据。根据TLE参数,容易得到航天器的轨道半长轴,若给定统计区域圆环的厚度,则可以得到圆环的内、外半径r1和r2。分析图2中的四种情况,可知空间物体通过该区域时,有效统计时间对应的第一个高度为圆环的内半径或空间物体近地点离地心的距离,第二个高度为圆环的外半径或物体远地点离地心的距离。针对不同的情况,分别将相应的高度值代入式(3)、式(9)或式(10),再根据式(6)计算得到空间物体与圆环的交点和近地点之间的时间差,以高度r的函数g(r)表示。
1)图2(a)中,空间物体轨道完全处于统计区域内,滞留时间为物体的轨道周期,即:Δt=T。
2)图2(b)中,物体的近地点位于统计区域内。其第一个高度为物体的近地点离地心的距离;第二个高度,即交点A2对应的高度值,等于r2。令r等于r2,根据式(2)~(10)可得A2与近地点之间的时间差g(r2),空间物体在统计区域内的滞留时间为该时间差的2倍,即:Δt=2g(r2)。
3)图2(c)中,物体的远地点位于统计区域内。其第一个高度应为交点A3对应的高度值,等于r1;第二个高度为空间物体的远地点离地心的距离。令r为r1,得A3与近地点之间的时间差g(r1),此时,空间物体的滞留时间为半轨道周期与该时间差的差值的2倍:Δt=2(T/2-g(r1))。
4)图2(d)中,两个交点高度对应的值分别为圆环的内、外半径,分别将r1和r2代入计算,根据式(2)~(10)可得交点A4和B4与近地点之间的时间差,分别为g(r1)和g(r2),物体的滞留时间为这两者之间差值的2倍:Δt=2(g(r2)-g(r1))。
对于穿越统计区域圆环的空间物体,根据上述不同的轨道运行情况,可以得到该空间物体相应的滞留时间。计算航天器在统计区域内的总碰撞通量时,本文采用依次计算其与单个物体的碰撞通量再累加的办法。记物体j的滞留时间与其轨道周期的比值为nj,将nj代替式(1)中的ntotal计算K值,进而得到该空间物体对航天器的碰撞通量。比值nj表示为:
nj=Δtj/Tj
(11)
2.2航天器基于椭圆轨道假设的碰撞通量
结合式(1)和式(11),可以得到航天器实际运行轨道中与空间物体发生碰撞的次数。航天器运动一个周期的总碰撞通量计算式如下所示:
(12)
式中:Kj、Ij分别表示物体j所代表的量,其余变量的含义同式(1)。
将航天器运动一周的碰撞通量乘以航天器一年的运动圈数,得到该航天器一年的总碰撞通量:
(13)
式中:T1为航天器运行一圈所花的时间,单位为s,Y表示1年,计算时需将其转化为s。
2.2.1 航天器碰撞通量计算
针对圆轨道假设和椭圆轨道假设两种情况,空间物体计入统计的判断条件有所不同。
圆轨道假设对应的理论认为,近地空间中,空间物体的轨道基本上为圆轨道,它们对碰撞概率的影响是主要的,大椭圆轨道对航天器的碰撞概率可以忽略不计。在这种情况下,只需要考虑轨道完全包括在统计区域圆环内的空间物体。通过选取航天器平均轨道高度上下各一定空间范围内确定的统计区域,只要空间物体的远、近地点高度均位于统计区域内,就令nj为1,再代入式(12)和式(13)计算该空间物体对航天器的年碰撞通量。
然而,在该假设中,要求统计区域足够大,才可能得到可靠的计算结果。这是因为,统计区域取得过小,符合条件的空间物体数量就很少,与实际空间环境相差较大,所得碰撞通量与实际值相差较大。并且统计区域取得过小,区域厚度微小的变化就可能导致碰撞通量值的较大波动,这将导致计算结果的不稳定。
椭圆轨道假设中,考虑了空间物体实际处在统计区域内的有效轨道,包括了图2中的四种情况。即空间物体的近、远地点均位于统计区域内(图2(a));空间物体的近、远地点有一个处在统计区域内,另一个在区域外(图2(b)~2(c));空间物体的近地点和远地点都不在统计区域内,但中间的一部分轨道处在区域中(图2(d))。将部分或全部轨道都处在统计区域内的空间物体计入统计,计算它们在统计区域内的滞留时间,再利用式(12)和式(13)计算这些物体对航天器的碰撞通量。
2.2.2 参数取值分析
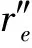
取航天器的高度为其轨道高度的平均值;取航天器高度的上、下各150 km作为统计区域,即厚度h=300 km;空间物体的大小不一,小的为几毫米,大的可达几十米, TLE编目目标中,最小空间物体的尺寸约为10 cm,考虑到物体的尺寸越小,数量越多,本文将空间物体的半径取为20 cm,将该值加上航天器的半径值即得到碰撞半径rA;积分上限取两物体的倾角中较小正弦值对应的轨道倾角或其补角。那么,若令航天器和空间物体的轨道倾角分别为i1,i2,令sini=min(sini1,sini2),则θ″的取值为:
(14)
此外,为检验碰撞通量对统计区域厚度的灵敏度,本文还计算了厚度h= 5, 10, 20, 30, 40, 50, 100, 200 km时航天器的总碰撞通量。
2.2.3 航天器碰撞通量算法实现
本文使用TLE编目数据计算航天器的碰撞通量。提取编目目标的主要参数如轨道编号、轨道倾角、轨道半径等,然后将编目目标按轨道倾角进行分组。分组间距为5°,通过分析,所有编目的空间物体的轨道倾角最大值为150°,因而将物体按(0,5],(5,10],…,(145,150]分成30组。对每一组中的物体逐一计算,并分类显示其计算结果。
对TLE参数预处理后,提取统计区域内符合条件的目标,将其参数代入相应的计算式,得到其对航天器的碰撞通量。根据圆轨道和椭圆轨道两种假设对应的理论,圆轨道假设下,当空间物体的远、近地点轨道高度均在统计区域内时,将该物体的参数代入计算;椭圆轨道假设下,只要空间物体有轨道在统计区域内,就将该物体的参数代入计算,也就是说,除了考虑物体的近地点或远地点在统计区域内的情形,还应该考虑空间物体的轨道横跨统计区域的情况。此外,圆轨道假设下,对计入统计的空间物体,令式(11)中的nj为1,再代入式(12)计算其对航天器的碰撞通量;椭圆轨道假设下,对满足条件的空间物体,则应该判断物体轨道相对统计区域圆环的位置关系,进而根据不同的情况计算物体在区域内的滞留时间,再代入式(12)计算航天器的碰撞通量。图3给出了圆轨道和椭圆轨道假设下的程序计算流程图,图中对两种假设条件下空间物体的判断依据进行了区分。
3 计算结果对比与分析
以铱星86(NOARD ID: 25528)为例,计算了其在圆轨道和椭圆轨道两种假设条件下的碰撞通量。取铱星的半径为5 m,根据TLE数据,得到其主要参数如表1所示。根据式(12)得到铱星86运行一圈的碰撞通量,再由式(13)计算得到一年的总碰撞通量。
表2给出了厚度h=5,10,20,30,40,50,100,200,300 km时,铱星86的年总碰撞通量以及计入统计的空间物体数量。
对比两种情况下铱星86的数据统计结果发现,圆轨道假设下空间物体的统计数量随着统计区域厚度的增加波动幅度较大,由统计区域厚度为5 km时的72个增加到厚度为300 km时的4000多个。将圆轨道假设与椭圆轨道假设的统计值相比,后者对前者的比值由60倍降低为2倍。就空间物体对铱星86的碰撞通量来看,椭圆轨道假设与圆轨道假设的计算值之比由大约4倍降为1.4倍。
图4给出了铱星86的统计区域内圆轨道和椭圆轨道两种假设情况下计入统计的空间物体轨道偏心率分布情况。限于篇幅,这里只给出h= 10,50,100 km的偏心率分布图。其中,左列为圆轨道假设下空间物体的偏心率分布;右列为椭圆轨道假设下空间物体的偏心率分布。所有计入统计的空间物体按偏心率(0,0.01],(0.01,0.02],(0.02,0.03],(0.03,0.04],(0.04,0.05],(0.05,0.1],(0.1,0.2],…,(0.8,0.9]进行分组,统计每一组空间物体的数量。
由图4可知,对于计入统计的空间物体,其轨道大部分属于近圆轨道。但由于圆轨道假设将统计目标的轨道严格限定在统计区域内,使得当统计区域厚度较小时,很大一部分没有完全处于统计区域的近圆轨道空间物体被排除,从而造成了较大的计算误差。
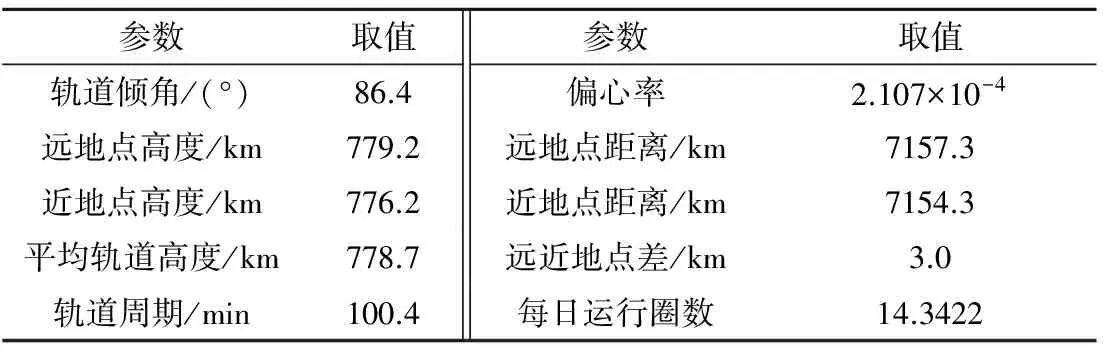
表1 铱星86的主要轨道参数Table 1 Orbital elements of the Iridium satellites 86
假设某空间物体的远、近地点轨道高度正好等于统计区域圆环的外半径和内半径,则其对应的偏心率最大。取铱星86统计区域厚度h=300 km,此时,内圆环半径为7005.8 km,外圆环半径为7305.8 km,圆轨道假设中符合条件的空间物体的最大偏心率约为0.021。
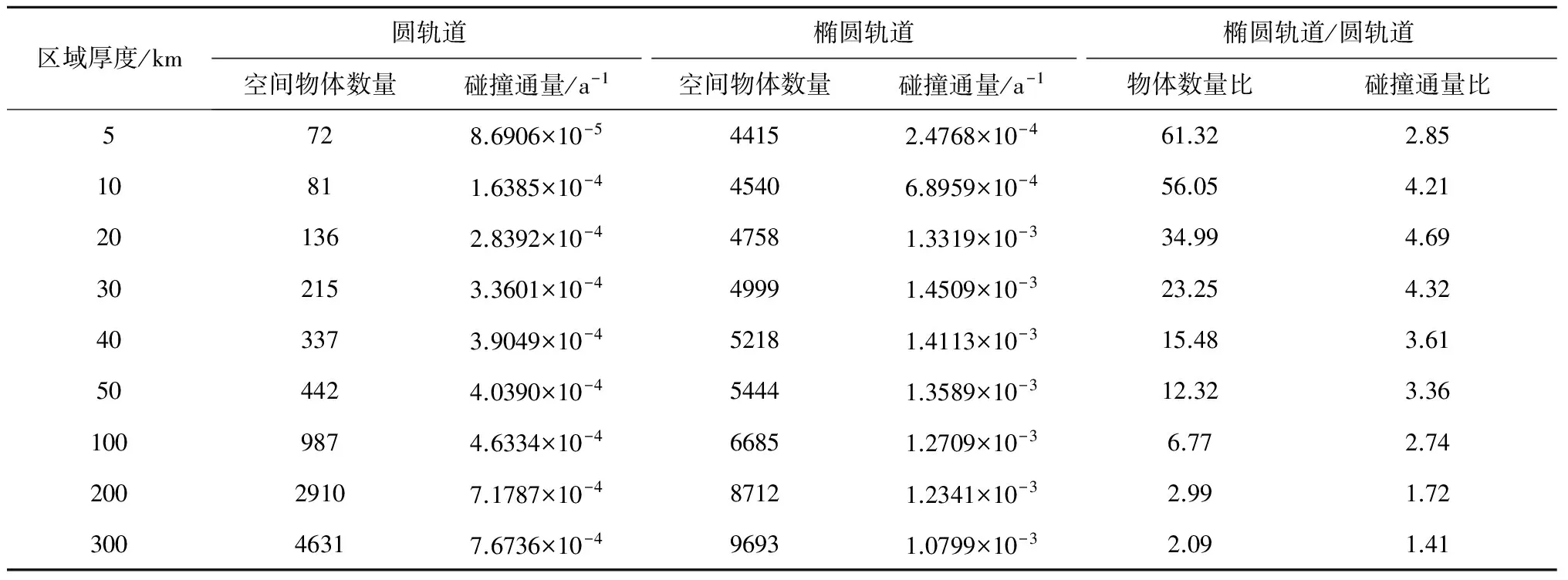
表2 不同区域厚度下铱星的碰撞通量Table 2 Number of collisions of Iridium satellite in different layer thickness
根据图4,当统计区域厚度较大时,两种假设条件下的碰撞通量计算结果比值较小,但仍然有很大一部分空间物体被圆轨道假设条件排除。例如,当统计区域厚度为300 km时,偏心率大于0.021的空间物体将被排除;小部分偏心率小于0.021的空间物体因为满足图2(b)~2(d)的情形被圆轨道假设条件剔除。这造成了统计结果的不准确,进而影响到碰撞通量的计算结果。
椭圆轨道假设中,部分计入统计的空间物体偏心率较大,但因为将滞留时间率作为空间物体的统计数量用于计算碰撞通量,所考虑的情形与实际空间环境相符,可以避免由于遗漏空间物体造成计算结果的不准确。
4 结 论
考虑空间物体椭圆运行轨道实际,本文根据开普勒方程和空间物体运动方程,采用陈氏模型,提出了空间物体椭圆轨道假设下航天器碰撞通量的计算方法。通过比较铱星86在两种轨道假设下的计算结果发现,随着统计区域厚度的增加,椭圆轨道与圆轨道的碰撞通量之比从大约4倍降为1.4倍。
由于在空间尺度上进行计算,小偏心率的空间物体也可能具有较大的远、近地点高度差。这些空间物体由于穿越统计区域而对航天器的碰撞通量有贡献。圆轨道假设只将轨道完全处于统计区域内的空间物体计入统计,忽略了图2(b)~2(d)的情况,与实际的空间环境相差较大;椭圆轨道考虑了空间物体的实际运动情况,可以避免遗漏统计目标,提高计算结果的准确度。
[1] 柳森, 兰胜威, 李毅, 等. 航天器解体模型研究综述[J]. 宇航学报, 2010, 31(1):14-23.[Liu Sen, Lan Sheng-wei, Li Yi, et al. Review of spacecraft breakup model[J]. Journal of Astronautics, 2010, 31(1): 14-23.]
[2] 李怡勇, 沈怀荣, 李智, 等. 航天器撞击解体碎片的短期危害评估[J]. 宇航学报, 2010, 31(4):1231-1236.[Li Yi-yong, Shen Huai-rong, Li Zhi, et al. Assessing the short-term hazard of spacecraft collision breakup debris[J]. Journal of Astronautics, 2010, 31(4): 1231-1236.]
[3] NASA. Orbital debris quarterly news[EB/OL]. 2016[2017]. https://orbitaldebris.jsc.nasa.gov/quarterly- news/pdfs/odqnv20i4.pdf.
[4] 白显宗, 陈磊, 张翼, 等. 空间物体碰撞预警技术研究综述[J]. 宇航学报, 2013, 34(8):1027-1039.[Bai Xian-zong, Chen Lei, Zhang Yi, et al. Survey on collision assessment and warning techniques for space objects[J]. Journal of Astronautics, 2013, 34(8): 1027-1039.]
[5] Foster J L, Wortham M B. ISS debris avoidance maneuver threshold analysis[R]. Washington, USA: National Aeronautics and Space Administration, May 2007.
[6] Carpenter J R, Markley F L. Wald sequential probability ratio test for space object conjunction assessment[J]. Journal of Guidance Control and Dynamics, 2014, 37(5): 1385-1396.
[7] Zhou W P, Guo X Z, Shen M, et al. Discussion on collision probability threshold[J]. Journal of Beijing Institute of Technology, 2015, 24: 61-65.
[8] Kessler D J. Derivation of the collision probability between orbiting objects: the lifetimes of Jupiter’s outer moons[J]. Icarus, 1981, 48(1): 39-48.
[9] Wang D F, Pang B J, Xiao W K. GEO space debris environment determination in the Earth fixed coordinate system[C]. 7th European Conference on Space Debris, Darmstadt, Germany, April 18-21, 2017.
[10] Foster J L, Frisbee J H. Comparison of the exclusion volume and probability threshold methods for debris avoidance for the STS orbiter and international space station[R]. Washington, USA: National Aeronautics and Space Administration, May 2007.
[11] Liou J C, Matney M J, Anz-meador P, et al. The new NASA orbital debris engineering model ORDEM2000[R]. Houston, USA: Johnson Space Center, May 2002.
[12] Matney M. NASA’s orbital debris environmental model ORDEM 3.0-implications for measurements and modeling[C]. 33rd Inter-Agency Space Debris Meeting, Houston, USA, March 30-April 2, 2015.
[13] Klinkrad H. Space debris models and risk analysis[M]. Chichester: Springer-Verlag, 2006.
[14] 刘舒莳, 龚建村, 刘四清, 等. 中长期轨道预报中大气阻力系数补偿算法的研究[J]. 宇航学报, 2013, 34(2):157-162.[Liu Shu-shi, Gong Jian-cun, Liu Si-qing, et al. Atmospheric drag coefficient calibration in medium-term orbit prediction[J]. Journal of Astronautics, 2013, 34(2): 157-162.]
[15] 刘卫, 王荣兰, 王四清, 等. 基于小波变换的卫星阻力系数分析[J]. 宇航学报, 2015, 36(2):142-150.[Liu Wei, Wang Rong-lan, Wang Si-qing, et al. Analysis of satellite drag coefficient based on wavelet transformation[J]. Journal of Astronautics, 2015, 36(2): 142-150.]
[16] Chan F K. Spacecraft collision probability[M]. California: The Aerospace Press, 2008.
[17] Dennis N G. Probabilistic theory and statistical distribution of Earth satellites[J]. Journal of the British Interplanetary Society, 1972, 25: 333-376.
[18] Zhou W P, Chan F K. Comparison of debris collision fluxes for the international space station[J]. Journal of Beijing Institute of Technology, 2016, 25: 41-49.
[19] 陈俊宇, 李彬, 章品,等. 低轨道空间碎片弹道系数及应用[J]. 红外与激光工程, 2016, 45(11).[Chen Jun-yu, Li Bin, Zhang Pin, et al. Low Earth orbit space debris ballistic coefficients and their applications[J]. Infrared and Laser Engineering, 2016, 45(11).]
CalculationsandAnalysisonImpactFluxesforSpaceObjectsunderAssumptionofEllipticalOrbits
ZHOU Wei-ping1,2, SHEN Ming1, GAO Peng-qi1, GUO Xiao-zhong1, ZHAO You1
(1. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)
This paper studies the impact fluxes calculation for the orbiting space objects via the Chan’s model which does not invoke either the kinetic theory of gases model or the Poisson distribution function. Four cases are discussed for the space objects on elliptical orbits passing through a thin spherical shell surrounding the spacecraft. The paper also compares the circular orbit assumption with the elliptical assumption. The satellite Iridium 86 is used to estimate the impact fluxes under both assumptions. It shows that the ratio of the impact flux between the elliptical orbits case and the circular case decreases from about 4 times to 1.4 times as the thickness increases. The statistical number of the objects gets a big fluctuation as the increased thickness in circular case. The elliptical case is 60 times more than the circular case when the shell’s thickness equals to 5 km.
Collision warning; Impact flux; Space objects; Spacecraft; Satellite orbits
V528
A
1000-1328(2017)11- 1234- 09
10.3873/j.issn.1000- 1328.2017.11.013
2017- 04- 18;
2017- 09- 05
国家重大科研装备研制资助项目(ZDYZ2013-2)
周威萍(1990-),女,博士生,主要从事空间物体碰撞概率阈值研究工作。
通信地址:北京市朝阳区大屯路甲20号国家天文台(100012)
电话:18210938053
E-mail:wpzhou@nao.cas.cn
赵有(1964-),男,博士,研究员,主要从事空间物体与碎片监测预警的研究工作。本文通信作者。
通信地址:北京市朝阳区大屯路甲20号国家天文台(100012)
电话:64807617
E-mail:youzhao@nao.cas.cn

