多模式复合交通网络方式划分两阶段模型研究

刘华伟，于晓桦，牟振华，王冲，张兴雅

（山东建筑大学交通工程学院，山东济南250101）

多模式复合交通网络方式划分两阶段模型研究

刘华伟，于晓桦*，牟振华，王冲，张兴雅

（山东建筑大学交通工程学院，山东济南250101）

对城市多模式复合交通网络进行有效的方式划分，能够提高交通分配和交通需求预测的准确性。文章提出了一种融合了出行者个人和交通网络特性的多模式复合交通网络方式划分的两阶段模型，并基于上海中心城区交通调查数据，通过算例对其进行验证。结果表明：两阶段模型中的第一阶段，小区1～6的单一出行方式和组合出行方式的选择概率分别为39.3%和60.7%，拆分的公交—轨道组合出行方式的选择概率为46.42%，单一和组合出行方式的选择概率更为精确；而第二阶段，小区1～6公交—轨道组合方式的OD矩阵被拆分为公交出行和轨道出行2种单一方式OD矩阵，其支持常用交通规划软件的运行与仿真。

交通规划；复合交通网络；两阶段模型

0 引言

多模式复合交通网络是指有规则指向的多模式叠加、复合的交通网络，包括道路网（小汽车网和慢行交通网）、公交网、轨道网和换乘枢纽［1-3］。在多模式复合交通网络中，由于轨道交通对客流的强大吸引及网络自身限制，越来越多的出行者选择各种交通方式与轨道交通的接驳换乘完成出行。因此，出行方式并非单一交通方式的简单叠加，而是由单一交通方式和组合交通方式共同构成的出行选择集。在实际工作中，常用的交通规划软件（TransCAD、Vissum、EMME等）只适用于单一模式网络分析，对于通过换乘点连通的多模式复合交通网络适用性差，需将全方式OD（Orient-Destination）矩阵通过交通方式选择拆分成各单一方式的OD矩阵输入软件。拆分带有组合方式的OD矩阵时，要充分考虑交通方式和换乘点的选择。

基于随机效用最大化的离散选择模型是最常用的交通方式划分方法，通过对出行者特征及偏好的调查标定效用函数，通过模型的集计将全方式OD矩阵分为单一方式的OD矩阵。然而由于组合交通方式的加入，这种方法已不能满足在多模式网络中交通方式划分的要求。因此，罗艺等与卫振林等在复合交通网络方式划分的研究中将轨道交通车站单独看作一类用地类型加以分析，从而避免轨道车站的换乘问题［4-5］。而现实中出行者是将轨道车站看作为一个中转地而非最终目的地进行出行决策的，因此模型不符合出行者出行选择心理，预测结果缺乏说服力。多位研究人员从网络本身结构出发，通过计算交通模式的路段阻抗与换乘弧阻抗，分析带有出行换乘的交通网络分配［6-8］。但是这种基于网络和统计学的分析方法，忽略了用户本身对方式选择的偏好，存在一定的局限性。

文章提出了一种融合了出行者的个人和交通网络特性的多模式复合交通网络方式划分两阶段模型基于用户出行的偏好，以出行效用最大化为标准，进行单一交通方式和组合交通方式的划分，而且对于组合交通方式，在交通网络结构分析的基础上，进行换乘点的选择，从而将居民出行全方式OD矩阵，拆分为交通软件仿真平台中所需的单一交通方式OD矩阵。并基于上海中心城区交通调查数据，给出算例并验证实用性。

1 多模式复合交通网络方式划分两阶段模型假设

对于一个多模式复合交通网络，节点和线路联系都非常复杂，考虑实际操作的可行性，避免在分析中生成过多OD点，在划分交通小区时各小区最多只有一个轨道交通车站，且在换乘点选择时车站编号与该小区编号一致，从而可将车站与所属小区视为网络中的一个节点进行分析。通过交通调查获取各小区之间居民出行的全方式OD矩阵。

对多模式复合交通网络中的连接线进行如下界定：

（1）城市复合交通网络由道路网、公交网和轨道网三类子网通过模式换乘枢纽锚固叠加而成。

（2）慢行交通受距离限制，用转移曲线法进行分离，单一交通方式仅考虑小汽车、公交车和轨道。

（3）如图1所示，以轨道交通为主体，考虑其他交通方式与轨道的接驳换乘关系，典型组合交通的5种方式有：公交车—轨道、小汽车—轨道、轨道—公交车、小汽车—轨道—公交车、公交车—轨道—公交车等。非机动车与轨道交通的接驳也是常见的居民出行方式组合，但慢行交通出行距离基本在轨道交通车站影响区域内，属于交通小区内部出行，故将该出行方式视为单一的轨道出行方式以简化模型计算。

图1 典型的组合交通方式示意图

2 多模式复合交通网络方式划分两阶段模型的建立

两阶段模型是将复合网络中的“交通方式划分”分解成两个阶段完成。模型的第一阶段，交通出行划分为单一方式与组合方式；模型的第二阶段，考虑换乘点选择，将组合方式再划分为单一方式的组合，并实现在复合网络中的分配。

2.1 模型第一阶段——单一方式与组合方式的划分

为避免Logit模型的IIA特性，选用NL（Nested-Logit）模型构建单一方式与组合方式划分模型。NL模型的上层为单一方式类和组合方式类的选择，下层为不同交通方式的集合，如图2所示。采用“阶段计算法”计算该模型［9-10］，模型下层作为独立模型进行参数估计，上层模型的效用是下层所有选择枝的函数。出行者是否选择组合交通方式取决于组合交通方式整体的效用，而组合交通方式整体的效用是各种不同组合方式所有变量的函数。

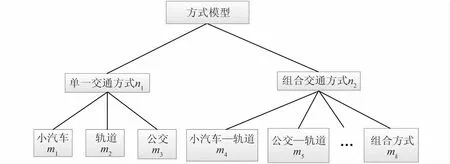
图2 基于出行方式类型的NL模型树状图

设M为可选择的出行方式的集合，则M＝（m1，m2，…，mi）；以N为上层选择项的集合，则 N＝（n1，n2），出行者选择选择方式 mi的概率 P（mi）由式（1）表示为

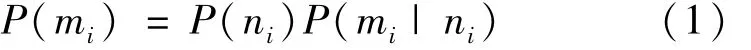
出行者选择上层选择项ni的条件下选择方式mi的概率P（mi｜ni）和出行者选择上层选择项ni的概率 P（ni）分别由式（2）、（3）表示为

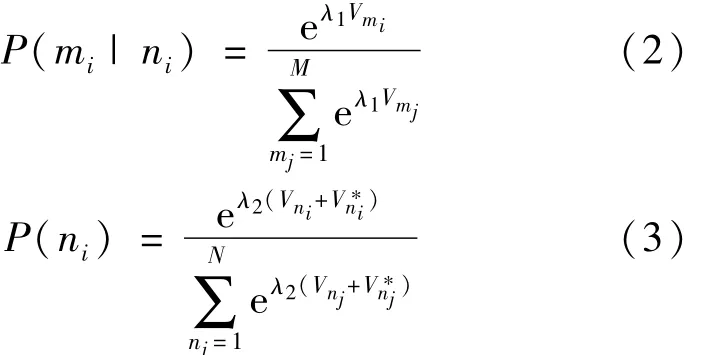
式中：Vmi、Vmi分别为出行方式选择项 mi、mi的出行效用；λ1、λ2分别是只同下层有关的效用概率项的方差相对应的参数，以及与同时考虑上、下层的效用的概率项方差相对应的参数（λ1、λ2应该满足1≥λ2／λ1＞0，否则上下层交换，各巢重新划分；当 λ1＝λ2时，模型为通常的多项Logit模型）；称为合成效用项，亦称为“logsum”。logsum表示期望效用，常被用于包含多个子选项的选择方案的整体评估中。当某个选择方案中的子选项相互独立，且效用函数为线性时，则此方案的期望效用为logsum形式，即

由式（2）、（3）与（1）表示为

需要说明的是，出行效用是出行者选择交通方式的衡量标尺，也是非集计模型建立的基础。在带有组合交通方式的方式划分中，将组合交通方式看作一种出行选择，其效用函数包括个人特征、方式效用和节点效用［11-13］。个人特征包括性别、年龄、月收入等变量，由交通调查的数据经过处理分析得到。方式效用取决于路段距离、时间消耗、费用、服务环境等因素，目前广泛采用线性形式，由式（6）表示为

换乘节点的效用t′则用步行时间、候车时间、换乘时间、出行费用、舒适性、可靠性等综合费用指标表示，由式（7）表示为

式中：tb为从出行起点步行到枢纽车站的时间，min；tw为等车时间，min；hij为从交通方式i到j的换乘步行时间，min；tp为出行费用转化为时间概念，min；ts为舒适度转化时间，min；tr为可靠性转化时间，min；α为步行惩罚因子；β为换乘惩罚因子。

效用函数需要调查数据进行标定与计算。由此，将全方式出行拆分为单一方式和组合方式的出行，而模型下一阶段是将组合出行以换乘点为断点拆分为单一方式出行。

2.2 模型第二阶段——组合方式换乘点选择

出行者在选择组合交通方式时，不同交通方式之间的换乘是影响用户选择的主要因素，换乘过程中存在的换乘步行时间和等待时间以及换乘费用增加了出行者的出行成本。在实际的出行中，出行者总会选择最合适的换乘点并尽量减少换乘次数。而换乘点又是各种交通方式组合在一起的锚固点，因此，多模式复合交通网络可以通过多模式路径和换乘弧转化为平面抽象网络［14-15］。

在图3所示的多模式复合网络中，出行者可在①、②、③、④、⑤、⑥代表的换乘枢纽节点进行换乘。如选择组合方式公交车—轨道的出行者，可在节点③和节点⑤选择换乘。将公交车—轨道交通方式表示为两条路径，形成如图4所示的公交—轨道组合方式的虚拟网络。在组合方式虚拟网络中，节点表示为 A（i，j，k），其中 i为节点编号；j为方式编号，小汽车、公交车、轨道的编号分别为1、2、3；k为换乘状态，k＝1表示用户到达该换乘点，k＝0表示用户已经历换乘从换乘点出发。因此，两个节点表示实际网络中的一个换乘点，称为换乘弧，其权重表示换乘阻抗。由于用户总是以最短路径选择出行方式，因此当换乘点之间存在多条路径时，将最短路径作为网络的路径边，其权重表示路径阻抗。

图3 多模式复合交通网络图

图4 公交车—轨道虚拟网络示意图

在一个带换乘弧的抽象网络中，阻抗是影响用户选择的主要因素，分为换乘阻抗和路径阻抗。模型第二阶段中的关键技术，就是根据不同模式及模式间换乘考虑阻抗函数形式，进行阻抗分析。

（1）道路阻抗

组合方式抽象网络中，道路阻抗即为路径阻抗，是多段路段阻抗的和，分为路径时间阻抗和路径费用阻抗，由式（8）表示为

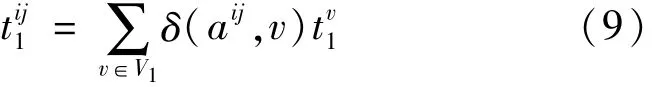
（2）公交网阻抗

公交阻抗由路径费用阻抗和路径不舒适性阻抗组成，由式（11）表示为

公交车的行驶是占用道路资源的，但公交车有自己的行驶路线和固定的发车时间。出行者在选择公交出行时，通常不会考虑公交路径的拥挤情况，而会选择先到的并可以到达目的地的公交车乘坐。但是如果公交车车内环境拥挤或者容量不足，出行者很可能会选择其他的车辆或路线［14-15］。因此公交阻抗反映为车内环境的不舒适性，即随着车内乘客的增加，车内的不舒适性也随之增加。单位时间内公交路段的不舒适性可以用BPR函数形式表示，随着乘坐公交时间的增加，不舒适性也会增加，则公交路段的不舒适性由式（12）表示为

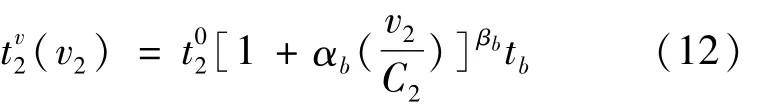
公交路径的不舒适性阻抗由式（13）表示为

（3）轨道网阻抗

轨道网阻抗与公交车阻抗类似，由式（14）表示为

（4）换乘弧阻抗

换乘阻抗包括换乘步行距离阻抗与换乘等待时间阻抗，由式（15）表示为

式中：ca为换乘阻抗；yai为换乘步行距离阻抗；cai为换乘等待时间阻抗；φ为权重。

换乘步行距离与车站的接驳交通设施布局有关，不同的车站布局形式，其步行距离也不相同。换乘距离要在乘客所能接受的距离之内，如果换乘距离大于乘客能够接受的换乘步行距离，其阻抗就将急剧增加，乘客有可能选择其他的交通接驳方式。BPR模型与需求函数特征非常吻合，因此借助BPR函数表示车站步行距离阻抗，由式（16）表示为

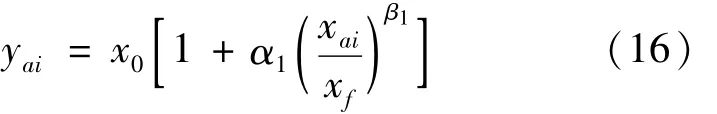
式中：yai为在a站换乘i方式的步行距离阻抗；xai为a站换乘i方式的步行距离，km；x0为表征阻抗的基本值；xf为乘客能够接受的换乘步行距离（等待时间），km；α1、β1为换乘步行阻抗影响参数。

只有当换乘轨道和公交车时才会出现等待时间，可以表示为排队长度、容量和发车频率的函数。为研究简便，文章仅考虑车辆容量与发车频率，借助BPR函数形式，在车站a换乘i方式的等待时间由式（17）表示为

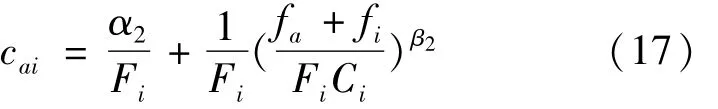
式中：cai为换乘等待时间阻抗；fa为在车站a上车的乘客数；fi为在a站之前线路上的乘客数；Fi、Ci分别为车辆的发车频率和车辆容量；α2、β2分别为等待时间影响参数。

利用用户平衡法（UE）或随机用户平衡法（SUE）在虚拟网络中对组合交通进行分配，得到各路段的流量，对应于实际网络中各方式的出行量，从而实现组合交通方式拆分为单一交通方式的组合形式。

3 算例分析

以上海中心城区交通调查实测数据标定模型第一阶段，然后构建交通网络进行模型第二阶段的求解。

3.1 模型第一阶段

为简化模型，选择小汽车、公交车、轨道、小汽车—轨道、公交—轨道等5种交通方式为研究对象，选择相应影响因素为效用变量，见表1。

表1 出行者交通方式选择行为的影响变量

NL模型参数估计，首先对下层出行方式选择模型进行参数估计，以单一出行方式中小汽车m3作为参照水平，其它交通方式与其进行对比，建立出行者各种交通方式的选择模型并利用最小二乘法标定，见表2。其中，V为估计值；t为t检验值。

表2 交通方式选择模型参数估计结果

表2中，估计值为某种交通方式发生概率与小汽车方式发生概率之比的参数估计结果，t检验为交通方式选择模型的估计参数值检验，如果t的绝对值大于1.65，而且参数符号正确，那么这个变量对选择枝产生影响的置信度是95%，表示该变量影响显著，NL模型概率函数包含自然指数的指数函数，求解采用两边取对数的形式，计算过程由式（18）表示为

以单一出行方式为参考对象得出参数估计结 果，见表3。

表3 出行方式类型模型参数估计结果

则组合出行方式相对于单一出行方式的概率发生比为

因此，结合两层选择的概率发生比公式，出行者同时进行出行方式类型和交通方式2个选择相对于选择单一方式中小汽车的概率发生比由式（19）表示为

假设通过模型的集计，从小区1～6的属性变量值 x1为 1、x2为3、x3为3、x4为0、x5为1、x6为5、x7为3、x8为0.3，由式（19）计算结果见表4。

表4 出行方式与交通方式选择结果

3.2 模型第二阶段

假设从小区1～6的路网结构为图3形式，以公交—轨道为例说明换乘点的选择计算过程，公交—轨道的抽象网络如图5所示。

图5 公交—轨道抽象网络图

路径①、②为公交出行路径，路径⑤、⑥为轨道出行路径，换乘点阻抗表示为③和④，算例没有对参数进行标定，假设所有参数均取1，各出行影响因素取值见表5。

表5 公交车—轨道出行方式影响因素

出行者出行的阻抗是其在交通网络上选择交通方式的路径阻抗经与经由换乘点的换乘弧阻抗的叠加，则经由换乘点③，使用路径①和⑤的总阻抗可表示为

式中：x为选择公交车—轨道的出行人数。

在本次调查数据中发现，从小区1～6出行者有256人，其中采用公交—轨道出行的用户为100人，其余为单一交通方式用户，全方式出行OD如下：

采用用户平衡法对各路径流量进行分配，可得图5中选择换乘点③的出行者为56人，选择换乘点⑤出行者为44人。拆分为下列出行OD：

经由换乘点③，在交通小区3公交换乘轨道到交通小区6的矩阵

经由换乘点⑤，在交通小区5公交换乘轨道交通到交通小区6的矩阵

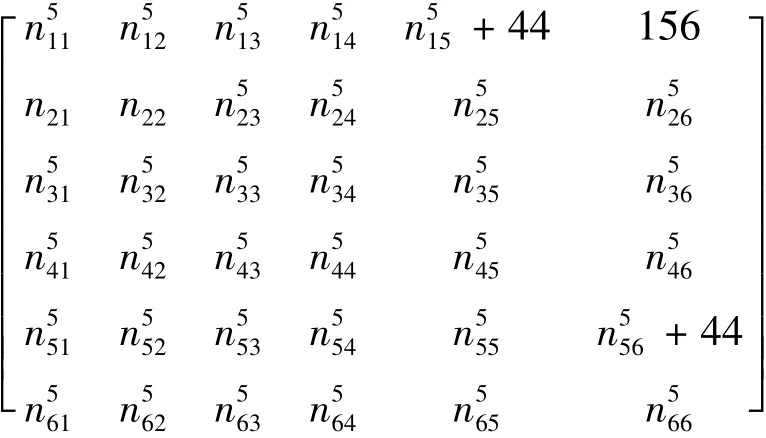
4 结论

文章提出了一种融合出行者个人和交通网络特性的多模式复合交通网络方式划分两阶段模型，并基于上海中心城区交通调查数据的计算实例，验证了模型的实用性，结果表明：

（1）第一阶段选用双层NL模型进行参数估计，通过分析影响出行者交通方式选择行为的因素以及各种出行方式的效用，得到小区1～6的单一出行方式和组合出行方式的选择概率分别为39.3%和60.7%，拆分的公交—轨道组合出行方式的选择概率为46.42%。克服了传统Logit模型IIA特性，使单一出行方式和组合出行方式的选择概率计算结果更为精确。

（2）第二阶段通过用户均衡模型将小区1～6公交—轨道组合方式的OD矩阵拆分为从小区1～3公交出行和小区3～6轨道出行的单一方式OD矩阵，以及小区1～5公交出行和小区5～6轨道出行的单一方式OD矩阵。输出的OD矩阵可直接支持常用规划软件的仿真输入要求，具有很强的实用性和可操作性，为规划工作者与交通规划软件开发人员提供了新的思路和借鉴。

［1］ 潘海啸.上海世博交通规划概念研究——构建多模式集成化的交通体系［J］.城市规划学刊，2005（1）：51-56.

［2］ Lo H.K.，Yip C.W.，Wan K.H..Modeling transfer and nonlinear fare structure in multi-modal network［J］.Transportation Research Part B-methodological，2003，37（2）：149-170.

［3］ Chen S.，Peng H.，Shuang L.，et al.A multimodal hierarchicalbased assignmentmodel for integrated transportation networks［J］.Journal of Transportation Systems Engineering＆Information Technology，2009，9（6）：130-135.

［4］ 罗艺，钱大琳.公交—地铁复合网络构建及网络特性分析［J］.交通运输系统工程与信息，2015，15（5）：39-44.

［5］ 卫振林，甘杨杰，赵鹏.城市复合交通网络的若干特性研究［J］.交通运输系统工程与信息，2015，15（1）：106-111.

［6］ 四兵锋，赵小梅，孙壮志.城市混合交通网络系统优化模型及其算法［J］.中国公路学报，2008，21（1）：77-82.

［7］ Olaru D.，Curtis C..Designing TOD precincts：accessibility and travel patterns［J］.European Journal of Transport and Infrastructure Research，2015，15（1）：6-26.

［8］ 叶霞飞，顾保南.城市轨道交通规划与设计（BZ）［M］.北京：中国铁道出版社，2010.

［9］ 陆化普.交通规划理论与方法［M］.北京：清华大学出版社，2006.

［10］关宏志.非集计模型交通行为分析的工具［M］.北京：人民交通出版社，2004.

［11］文雅，晏克非，成峰.基于出行链的城市客运交通枢纽换乘需求预测模型［C］.北京：中国交通运输协会现代客运枢纽分会成立大会暨学术交流会，2010.

［12］魏华，马荣国，赵跃峰，等.综合客运枢纽旅客换乘交通方式分担模型［J］.长安大学学报（自然科学版），2014，34（2）：94-98.

［13］左志，潘晓锋.基于有限理性的交通方式划分模型［J］.大连理工大学学报，2014（5）：531-536.

［14］于晓桦，刘华伟.基于轨道换乘的复合交通网络OD拆分重组技术［J］.交通运输研究，2016，2（5）：9-16.

［15］陈先龙.交通方式划分离散选择模型的比较研究［J］.交通运输工程与信息学报，2014（2）：28-35.

Research on two-stage traffic model splitting model of composite transportation network

Liu Huawei，Yu Xiaohua*，Mou Zhenhua，et al.
（School of Transportation Engineering，Shandong Jianzhu University，Jinan 250101，China）

Reasonable traffic modal splitting of composite transportation network ensures the accuracy of traffic assignment and traffic demand forecast.This paper puts forward a two-stage traffic model splitting modle which combines individual travel characteristics with transportation network characteristics.An example based on the data of Shanghai downtown traffic investigation is given to demonstrate the validity of thismodel.The results indicate that in the first phase of two-phasemodel，the selection probability of single mode and combined mode from zone 1 to zone 6 are 39.3%and 60.7%respectively，and the selection probability of the bus-rail is46.42%.In the second phase，the OD matrix of bus-rail combined mode from zone 1 to zone 6of is broken into two single forms of bus OD matrix and rail OD matrix，which support the operation and simulation of the commonly used traffic planning software.

traffic planning；composite transportation network；two-stagemodel

U491

A

1673-7644（2017）05-0467-07

10.12077／sdjz.2017.05.010

2017-09-15

山东省自然科学基金资助项目（ZR2013EEQ014）

刘华伟（1992-），男，在读硕士，主要从事城市综合交通规划等方面的研究.E-mail：1198371016＠qq.com

*：于晓桦（1983-），女，讲师，博士，主要从事交通运输规划与管理等方面的研究.E-mail：yuxiaohua＠sdjzu.edu.cn

（学科责编：赵成龙）