木结构古建筑抗震性能参数分析

张锡成，马赫迪，代武强，吴晨伟

（西安建筑科技大学 土木工程学院，陕西 西安710055）

木结构古建筑抗震性能参数分析

张锡成，马赫迪，代武强，吴晨伟

（西安建筑科技大学 土木工程学院，陕西 西安710055）

不同构造形式及其参数取值对木结构古建筑的动力特性及抗震性能有直接影响，因此研究参数变化对结构动力性能的影响规律，对于木结构古建筑的修缮与加固保护具有重要的指导意义。基于宋代《营造法式》制作了某单层单开间殿堂式木结构模型，建立了考虑柱础滑移隔震、榫卯半刚性连接及斗栱减震性能的空间杆系有限元模型，并与单向水平地震激励下的振动台试验进行了对比；通过参数分析探索了木结构斗栱、榫卯及屋盖等不同构造方式及相应结构参数取值的改变对其抗震性能的影响。结果表明：随着斗栱刚度的增大，整体结构的自振频率收敛于上限2.08 Hz，且其耗能减震作用逐渐变弱；随着榫卯节点的刚度逐渐变大，整体结构的自振频率收敛于上限3.26 Hz，柱脚的滑移量会随之增大而柱架侧移却随之减小，而榫卯节点刚度的减小在减少柱脚滑移量的同时会使得柱架的侧移变形大大增加，榫卯节点的刚度变化对结构自振频率的影响程度大于斗栱刚度；屋盖质量的增加会降低结构的自振频率，增大斗栱的水平变形，提高整体结构的抗震能力。

木结构古建筑；杆系模型；构造方式；抗震能力

0 引言

木结构建筑历史悠久，其丰富的科学和文化价值是中国乃至世界不可多得的瑰宝。近年来，许多学者通过试验和理论分析的方法对古建筑木结构的结构性能及抗震机理展开了大量科学研究，并取得了一系列的学术成果。谢启芳等通过对榫卯节点的抗震性能研究，建立了榫卯连接的恢复力模型［1-2］，并对斗栱力学性能进行了试验研究，得到了其荷载—位移滞回曲线［3］。高大峰等通过试验得到斗栱在竖向荷载作用下的力—位移关系曲线［4］。Fang等通过对西安北门箭楼木构架进行现场测试与理论分析，对其动力特性进行了研究［5-6］。周乾等以故宫太和殿为研究对象，通过对古建筑的榫卯节点、斗栱等构造特征进行数值模拟，分析了其抗震性能［7-9］。日本学者对日式传统木结构建筑进行了大量试验分析，对柱与础石的连接性能［10］、榫卯节点的半刚性性能［11］、斗栱的力学性能［12］及整体结构的抗震性能［13］进行了系统研究。

目前的研究主要针对某一特定的结构构件或者具体建筑进行分析，而不同构造形式及相关参数对木结构动力特性的影响规律方面研究较少。因此，在现有研究成果的基础上，通过对殿堂式木结构古建筑的有限元建模及参数分析，对斗栱、榫卯及屋盖等不同构造形式及其参数取值对其动力特性的影响，研究各参数变化对古建筑木结构抗震性能的影响规律，以期为木结构古建筑的修葺与加固保护提供理论依据。

1 木结构有限元分析模型的构建

1.1 简化分析模型

参照宋代《营造法式》制作了某单层单开间殿堂式木结构模型［14］，其模型构造形式及构件尺寸如图1所示。采用杆系单元与弹簧单元的组合形式建立殿堂结构计算模型如图2所示，其中各单元的选取原则为

图1 模型及构件尺寸图／mm

（1）柱、额枋及梁单元的选取

通常采用BEAM188梁单元处理线性、大角度转动及非线性大应变等问题，故柱、额枋及梁等构件的力学行为可用此单元来模拟。木材的正交各向异性可通过材性试验的实测数据来反映，采用该单元沿3个方向的弹性模量及泊松比来描述。

（2）柱与额枋的榫卯连接

在木结构古建筑中，柱与额枋之间的榫卯连接节点介于铰接与刚接之间，具有半刚性的特点。因此，节点在传递轴力、剪力、扭矩及弯矩作用的同时，又会产生一定的变形。其中，节点在受到弯矩作用所产生的转动变形为主要变形，其轴向拉压变形、剪切变形及扭转变形可以不予考虑，故采用弯矩—转角曲线榫卯节点的力学特性描述。因此，用类似于榫卯节点连接的非线性弹簧来进行有限元分析，以此达到简化分析的目的，在此采用COMBIN39弹簧单元来模拟榫卯节点的半刚性性能。

图2 殿堂结构的计算简图

（3）柱与础石的连接

在木结构古建筑的柱与础石之间，只能通过摩擦力来平衡水平荷载。当础石的最大静摩擦力大于水平荷载时，柱与础石之间类似于铰接连接，只发生转动变形；而当础石的最大静摩擦力小于水平荷载时，相对滑移就会产生。因此，柱与础石间的滑动摩擦力就是结构底部所能抵抗的最大水平剪力。这种情况下，在柱底加上一个虚拟的水平弹簧单元。当柱与础石之间的最大静摩擦力大于水平剪力时，此单元没有变形产生，此时弹簧刚度K为无穷大，而当最大静摩擦力小于水平剪力时，弹簧的内力不改变，且为最大静摩擦力，此时弹簧对柱脚不产生约束，即此时的K为零。因此，对滑移连接特性的模拟可以通过在柱脚与础石之间采用COMBIN40单元来完成。

（4）斗栱

在水平地震作用时，斗栱所要承受的力主要来自于上部屋盖梁架的自重及其传递的水平剪力。在通过力—变形曲线来描述斗栱力学特性时，可以采用水平及竖直2个方向的平动弹簧简化斗栱。水平弹簧单元可以用COMBIN14单元来模拟，斗栱在轴向压力作用下的力学性能可以通过把该单元设置为一维轴向弹簧—阻尼器来模拟，竖向弹簧单元则选择COMBIN39单元来模拟斗栱在水平力作用下的非线性特性。可以由四朵斗栱平均分担屋盖梁架系统的自重，且分担的质量集中作用在其顶部。通过以上分析，殿堂结构一榀平面构架的计算图如图2所示，柱底取至础石顶面，采用柱、额枋及乳栿的形心线作为各自的轴线，所示的弹簧单元几何尺寸都为零。空间模型也可按照上述的简化分析推广得到。

1.2 单元实常数的确定

（1）平动弹簧单元实常数

在相同条件的水平荷载作用下，通过低周反复荷载试验对振动台试验模型中的单朵斗栱进行分析［15］，得到了其恢复力特性，如图 3（a）所示。同时对振动台试验模型进行试验［4］，得到单朵斗栱在竖向荷载作用下的力学行为，如图3（b）所示。

对COMBIN39弹簧单元的实常数的定义可以根据图3（a）所示的水平力—侧移曲线确定。设置KEYOPT（1）＝1，即按照ANSYS内置的卸载准则定义COMBIN39弹簧单元的滞回规则符。卸载路径的卸载方向选择沿通过原点且平行的线段进行。

竖向力与竖向位移之间可近似看作线性关系，由图3（b）所示的竖向力—侧移曲线可得到。然后赋予COMBIN14单元实测得到的竖向刚度值，将试验数据进行线性拟合，COMBIN14单元的实常数项可选用得到的单朵斗栱的竖向刚度K为6 kN／mm，用此弹簧常数来进行斗栱的轴向性能的模拟。

图3 单元实常数确定图

（2）COMBIN39转动弹簧单元实常数

在水平荷载作用下，进行单榀柱架的低周反复荷载试验［15］。对榫卯节点的恢复力特性进行分析，得到节点弯矩—转角关系曲线，如图3（c）所示。根据此曲线可以定义COMBIN39弹簧单元的实常数。同样，按照ANSYS内置的卸载准则定义该单元的滞回规则，即设置KEYOPT（1）＝1。卸载路径选择沿过原点且与其平行的线段方向。

（3）COMBIN40单元实常数

制作了6组红松柱段与青石石板对静摩擦系数进行测定［14］。其所采用的是与振动台试验模型相同的材料、尺寸和制作工艺。红松与青石板之间的静摩擦系数经过试验测定其平均值μ为0.33。在简化计算模型当中，可以取单个柱所能承受的最大静摩擦力作为COMBIN40单元的临界滑动力，同时令滑动弹簧水平刚度K1为∞，弹簧二阶刚度K2为0，空隙GAP为0。

1.3 有限元模型的建立

在对结构的有限元分析模型进行参数化编程时，计算模型直接由ANSYS内置的APDL语言生成。柱脚与础石之间的滑移连接通过在柱脚位置处添加COMBIN40单元来模拟。在与柱脚节点重合的位置，额外生成4个节点，作为地面节点，对UX、UY、UZ、ROTX、ROTY、ROTZ 6个方向的自由度进行约束，4个柱脚节点在UZ、ROTZ等2个方向的自由度也同样被约束。柱脚摩擦滑移单元采用沿x、y向的COMBIN40单元分别将地面节点及柱脚节点进行连接形成。屋盖的质量通过在4个乳栿相交的节点处添加Mass21单元来模拟。因其转动惯性可忽略，故将其设置为2D单元。所建立的有限元模型如图4所示，KO和MO分别表示弹簧单元和质量单元。

图4 有限元计算模型图

1.4 地震模拟计算结果与验证

在对结构进行不同工况下的加速度地震波的瞬态动力分析后，将不同节点的计算结果采用ANSYS程序提取出来。由于只在一个方向输入地震波，且有限元计算模型的结构布置均匀对称，因此，不考虑结构扭转，标高相同处的加速度在水平方向上也大致相等，所以代表柱脚、柱架顶面及屋盖的测点可任意在柱底、柱顶及乳栿端的节点中进行选择。为验证所选取的有限元模型的准确性，通过对屋盖加速度以及相对位移反应进行研究分析，将所得到的计算结果与振动台试验结果［10］进行对比，如图5所示。

图5 兰州-50工况屋盖加速度及相对位移反应的计算值与试验值对比图

由图5分析可知，屋盖加速度反应和相对位移反应时程曲线的计算值与试验值吻合程度较高，到达峰值时刻也基本相同，说明所建立的模型单元一定程度上可以很好的模拟真实情况。

2 抗震性能主要参数分析

结合目前的研究成果［16］并考虑到影响古建筑木结构动力特性的因素，选取斗栱刚度kd、榫卯节点刚度kj及屋盖的质量m等主要参数，分别探讨斗栱、榫卯及屋盖不同构造方式的影响。通过修改空间杆系有限元模型的相关参数，对其进行拓展参数分析。

2.1 斗栱刚度

2.1.1 斗栱刚度与自振频率关系分析

设计算模型中斗栱的刚度为kd，原始结构中斗栱的初始刚度为kd0，则尺寸构造不同的斗栱可以用二者比值大小的变化来模拟，计算模型在不同斗栱刚度下的自振频率及周期见表1，并将表1中数据绘于图6。

表1 计算模型在斗栱刚度变化下的自振频率及周期

图6 斗栱刚度变化下计算模型的自振频率图

从图6可以看出，整个结构的自振频率明显受到斗栱刚度的影响。当kd／kd0＜10时，结构自振频率随着斗栱刚度的增大，增幅明显较快；当kd／kd0＞20时，结构的自振频率增幅放缓，最后自振频率收敛于上限 2.08 Hz。

2.1.2 斗栱刚度对抗震性能的影响

通过输入El Centro波300 cm／s2，并不断调整斗栱的刚度比值，对模型进行动力时程分析。不同刚度比值情况下试验得到的结构反应见表2。

表2 计算模型在斗栱刚度变化下各位置处的最大地震反应

由表2可看出，结构的地震反应直接受到斗栱刚度大小变化的影响。由图7可知，随着斗栱刚度的增加，柱脚、柱架及屋盖处的最大相对位移反应和最大加速度反应都明显增大，相反，斗栱的侧移变形却在减小。这是因为kd／kd0的增加使得结构的整体抗侧刚度提高，柱架及屋盖等上部结构的加速度反应因此而加大，导致结构的层间剪力变大。但由于kd／kd0的提高幅度远远大于层间剪力的增幅，所以斗栱的侧移变形才减小。

可用屋盖处与柱架顶面的动力放大系数来衡量斗栱的耗能减震作用效果。从图7（d）中可看出，随着kd／kd0的增加，动力放大系数在初期急剧上升，随后趋于稳定，并最终趋近于1。这说明，较小的斗栱刚度在耗能减震作用有着较好的表现。斗栱的耗能减震作用在其刚度不断增加时，逐渐减弱，直至屋盖的加速度与柱架顶面的加速度相同，此时斗栱的作用类似于刚体，侧移趋近于0，如图7（c）所示。因此，斗栱的刚度大小决定着斗栱耗能减震性能的强弱。斗栱刚度越小，其具备的变形性能越好，抗震时性能就发挥的越充分。

2.2 榫卯节点刚度

2.2.1 榫卯节点刚度与自振频率关系分析

设榫卯节点在计算模型中的抗弯刚度为kj，对应于原始结构的初始刚度为kj0，不同的榫卯连接方式可以通过调整二者比值的大小来模拟。表3给出了计算模型在榫卯连接刚度变化时的自振频率及周期。表3中，榫卯节点在kj／kj0＝∞时表现为刚性，而当kj／kj0＝0时，结构为可变体系，故可以不考虑此情况。将表3中数据绘于图8。

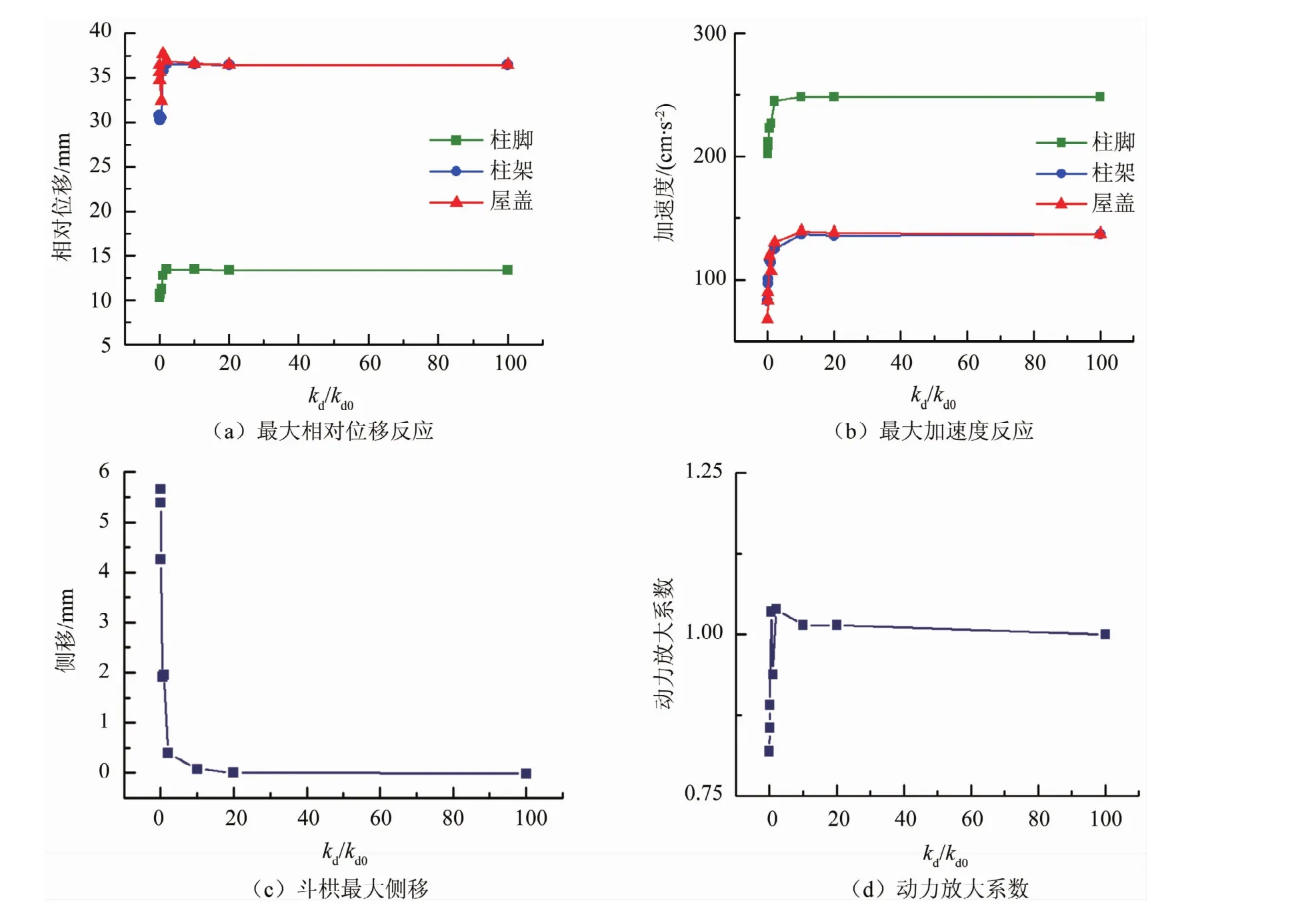
图7 斗栱刚度比变化下结构的最大地震反应及动力放大系数图

表3 计算模型在榫卯连接刚度变化下的自振频率及周期表

图8 榫卯连接刚度变化下计算模型的自振频率图

由以上数据可以看出，整个结构的自振频率与榫卯节点的刚度大小之间有着直接影响。当kj／kj0＜10时，结果的自振频率随着节点刚度的增大，增幅明显较快；当kj／kj0＞20时，结构的自振频率增幅放缓，最后收敛于上限3.26 Hz，此时，结构的自振频率就为节点刚接时结构的最大自振频率。结构自振频率在榫卯节点刚度变化时，所产生的影响较斗栱刚度对结构产生的影响更加明显。从表3可以看出，由榫卯节点刚度变化引起的频率波动范围为0.31～3.26 Hz，而斗栱刚度的变化在相同的刚度比值下所导致结构的自振频率波动范围仅为0.39～2.08 Hz。榫卯节点的刚度变化对结构自振频率的影响程度大于斗栱刚度的影响，榫卯节点刚度的大小对整体结构自振频率的高低起决定性作用。

2.2.2 榫卯节点刚度对抗震性能的影响

通过输入El Centro波300 cm／s2，并不断调整榫卯节点刚度的大小，对模型进行动力时程分析，得到的刚度比值情况变化下的最大结构反应见表4。

从表4可以看出，结构的地震反应直接受到榫卯连接刚度大小的影响。由图9可以看出，在相对位移反应方面，柱脚的滑移量随着节点刚度的增加而不断增大，而柱架的侧移变形却随之减小。这是因为柱架的整体抗侧刚度随着kj／kj0的增加而提高，使得结构的抗侧移变形能力增强，在减小柱架的侧向变形减小的同时，也造成了上部结构的加速度反应的增大，如图10所示。此时结构底部剪力也会因 此而变大，进而表现为柱脚的滑移量增大。

表4 计算模型在榫卯连接刚度变化下各位置处的最大地震反应

图9 节点刚度变化下的最大柱脚滑移量及最大柱架侧移变形图

图10 节点刚度变化下的各位置处的最大加速度反应图

由上述分析可知，榫卯节点处于木结构古建筑抗震减震体系中的关键地位，同时也是比较脆弱的部分。榫卯节点的刚度大小直接影响结构的抗震能力，节点刚度的增加使柱脚滑移量增大，柱脚容易滑出柱础造成结构落架倒塌；其刚度的减小则会使柱架的侧移变形增大，同样会导致结构发生倒塌破坏。所以，在进行木结构古建筑修缮加固时，应给出加固后合理的榫卯节点刚度区间，在保证柱架、屋盖处的相对位移和加速度反应处在允许范围内的同时，相应的柱脚滑移量不至于过大而导致结构倒塌。

2.3 屋盖质量

2.3.1 屋盖质量与自振频率关系分析

设计算模型中屋盖质量为m，原始结构中屋盖的质量为m0，不同形制构造的屋盖可用二者比值的大小来模拟。计算模型在屋盖质量变化时的自振频率及周期如图11所示。

由图11可以得知，结构的自振频率直接受到屋盖质量大小的影响。结构的自振频率在屋盖质量的增大的同时，随之降低。根据结构基本频率的计算公式也可以得到同样的结论，结构质量在刚度一定时，与基本频率成反比。结构的自振频率在结构质量无限大时，无限接近于0。

2.3.2 屋盖质量对抗震性能的影响

El Centro—300工况下屋盖质量比值情况变化下的最大结构反应见表5。

图11 屋盖质量变化时计算模型的自振频率图

由表5和图12可以看出，随着屋盖质量的增加，结构各位置处的加速度反应都在减小，而对应的相对位移反应却在增大。这是由于屋盖质量的增加延长了整体结构的自振周期，使之错开地震波的卓越周期。因此，增大了与输入激励的频率两者之间的比值，结构的加速度反应因此而减小。但是尽管如此，结构所受的地震惯性力由于屋盖质量的大大增加依然很大，这就使得结构各部分的剪力也同样很大，导致了各位置的层间变形的增大，如图13所示。

表5 屋盖质量变化下计算模型各位置处的最大地震反应

图12 屋盖质量比变化时的最大结构地震反应图

图13 屋盖质量比变化时各位置的最大侧移图

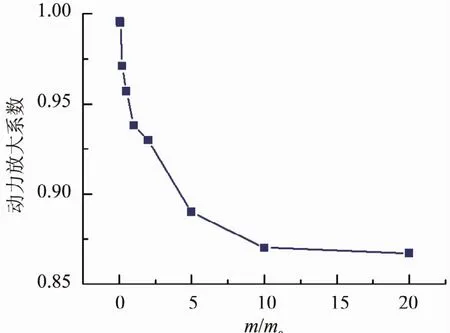
图14 动力放大系数图

分析斗栱的耗能减震作用所受到屋盖质量影响时，可通过衡量屋盖处与柱架顶面处最大加速度反应的动力放大系数来分析，如图14所示。斗栱在屋盖质量较小时，所受到屋盖传下来的剪力非常小，动力放大系数接近1，基本没有变形产生，因此斗栱没有发挥耗能减震能力。斗栱在屋盖质量的增加的同时，产生的水平变形也在增大，而同时，加速度动力放大系数减小，说明斗栱的耗能减震作用逐渐增强。

3 结论

通过上述研究表明：

（1）斗栱刚度的增加引起结构自振频率的增大，自振频率的增幅在kd／kd0＜10时较快，在 kd／kd0＞20时收敛于上限2.08 Hz；同时还使结构各位置相对位移和加速度反应增大，斗栱的侧移减少，说明斗栱减震耗能的作用随着其刚度的增加而减弱。

（2）榫卯节点刚度的增加引起结构自振频率的增大，自振频率增幅在 kj／kj0＜10时较快，在kj／kj0＞20时，收敛于上限 3.26 Hz；榫卯节点刚度的增加会造成柱脚的滑移量的增大以及柱架侧移的减小，而榫卯节点刚度的减小在减少柱脚滑移量的同时，使得柱架的侧移变形大大增加。榫卯节点的刚度变化对结构自振频率的影响程度大于斗栱刚度对其的程度，因此榫卯节点刚度的大小对整体结构自振频率的高低起决定性作用。

（3）结构的自振频率随着屋盖质量的的增大而降低，结构各部分产生的相对位移反应也大大增加，而其相对应的加速度反应却因此而减小，说明屋盖质量的增加可以使斗栱发生较大的水平变形，提高其减震耗能的作用。

［1］ 谢启芳，杜彬，向伟，等.古建筑木结构燕尾榫节点抗震性能及尺寸效应试验研究［J］.建筑结构学报，2015，36（3）：112-120.

［2］ 谢启芳，杜彬，钱春宇，等.古建筑木结构燕尾榫节点弯矩—转角模型研究［J］.工程力学，2016（8）：39-44.

［3］ 谢启芳，向伟，杜彬，等.古建筑木结构叉柱造式斗栱节点抗震性能试验研究［J］.土木工程学报，2015（8）：19-28.

［4］ 高大峰，赵鸿铁，薛建阳.中国木结构古建筑的结构及其抗震性能研究［M］.北京：科学出版社，2008.

［5］ Fang D.P.，Iwasaki S.，Yu M.H.，et al..Ancient Chinese timber architecture. I： Experimental study［J］.Journal of Structural Engineering-ASCE，2001，127（11）：1348-1357.

［6］ Fang D.P.，Iwasaki S.，Yu M.H.，et al..Ancient Chinese timber architecture.II：Dynamic characteristics［J］.Journal of Structural Engineering-ASCE，2001，127（11）：1358-1364.

［7］ 周乾，闫维明，关宏志.故宫太和殿结构现状数值模拟研究［J］.中国文物科学研究，2015（2）：79-84.

［8］ 周乾，闫维明，关宏志，等.故宫太和殿静力稳定构造研究［J］.山东建筑大学学报，2013，28（3）：215-219.

［9］ 周乾，闫维明，关宏志，等.故宫太和殿抗震性能研究［J］.福州大学学报（自然科学版），2013（4）：487-494.

［10］Maeno M.，Saito S.，Suzuki Y..Evaluation of equilibrium of force acting on column and restoring force due to column rocking by full scale test of traditional wooden frames［J］.Journal of Structural and Construction Engineering，Transactions of Architectural Institute of Japan，2007，615：153-160.

［11］Ogawa K.，Sasaki Y.，Yamasaki M..Theoretical modeling and experimental study of Japanese“Watari-ago”joints［J］.Journal of Wood Science，2015，61（5）：481-491.

［12］Kaori F.，Isao S.，Yoshimitsu O.，et al..Static and dynamic loading tests of bracket complexes used in traditional timber structures in Japan［C］.Auckland：The TwelfthWorld Conference on Earthquake Engineering，2000.

［13］Takatani T.，Nishikawa H..Seismic collapsing process analysis of one-story thatched roof wooden structure under strong earthquake ground motion［J］.Journal of Civil Engineering and Construction，2016，5（2）：114-125.

［14］Zhang X.C.，Xue J.Y.，Zhao H.T.，et al..Experimental study on Chinese ancient timber-frame building by shaking table test［J］.Structural Engineering and Mechanics，2011，40（4）：453-470.

［15］隋龑.中国古代木构耗能减震机理与动力特性分析［D］.西安：西安建筑科技大学，2009.

［16］张锡成.地震作用下木结构古建筑的动力分析［D］.西安：西安建筑科技大学，2013.

Parametric analysis of seismic performance of ancient timber-framed buildings

Zhang Xicheng，Ma Hedi，DaiWuqiang，et al.
（School of Civil Engineering，Xi'an University of Architecture and Technology，Xi'an 710055，China）

The different structural forms and their parameters directly affect the dynamic characteristics and seismic performance of the ancient timber-framed buildings.The influence of the change of the parameters on the dynamic performance of the structure is studied by the finite element modeling and parameter analysis.Itwill provide reference for the repair and reinforcement of ancient timber-framed buildings.Based on themodel of a single-storey place housemade by Ying Zao Fa Shi of the Song Dynasty，a 3-D beam-spring FEM model is established，which involves the sliding isolation of column root，energy dissipation of Dou-gong and semi-rigid behavior of mortise-tenon joints.Then a comparison is made with the shaking table test under unidirectional earthquake excitations.Furthermore，a parametric analysis is conducted through the change of structural configuration such as mortise-tenon joint，Dou-gong and roof and corresponding parameters.The results show that：with the increase of the lateral stiffness of Dou-gong，the natural frequency of the whole structure converges to the upper limitof2.08 Hz，the ability of shock absorption of the structure becomesweaker.With the increase ofmortise-tenon joints stiffness，the natural frequency of the whole structure converges to the upper limit of 3.26 Hz，while the slippage of the column increased and thelateral displacement of the column reduced.With the reduction of the stiffness of the mortise-tenon joints，the slippage of the column reduced while the lateral displacement of the column increased at the same time.The influence of the stiffness change of the mortise-tenon joints on the building's natural frequency is greater than that of the Dou-gong.The natural frequency of the structure reduced by the increase of the roofmass，while the deformation of the Dou-gong increases and helps improve the seismic capacity of the whole structure.

ancient timber-frame buildings；beam-column elementmodel；structural configuration；seismic capacity

TU366.2

A

1673-7644（2017）05-0426-09

10.12077／sdjz.2017.05.004

2017-08-18

国家自然科学基金项目（51508454）；陕西省自然科学基础研究基金项目（2016JQ5060）；陕西省教育厅科研计划项目（15JK1444）；西安建筑科技大学青年科技基金项目（QN1612）；西安建筑科技大学人才科技基金项目（RC1404）

张锡成（1984-），男，讲师，博士，主要从事古建筑木结构抗震及加固保护等方面的研究.E-mail：xicheng-zhang＠163.com［*

］

（学科责编：赵成龙）