改进的Gabor变换和二维NMF融合的人脸识别

王晓华，杨清梅，杨 涛

西安工程大学 电子信息学院，西安 710048

改进的Gabor变换和二维NMF融合的人脸识别

王晓华，杨清梅，杨 涛

西安工程大学 电子信息学院，西安 710048

为了得到高质量的人脸特征，提高人脸识别性能，提出基于改进的Gabor变换和（2D）2NMF（二维非负矩阵分解法）的人脸识别方法。改进的Gabor变换提取的特征有较高的品质，鲁棒性增强。二维非负矩阵分解法降维能大大降低图像数据维数，缩短计算时间，提高识别率。最后在ORL人脸库中进行实验，结果表明改进的Gabor变换和二维NMF方法相结合计算时间略微增加，但识别效率明显提高，从而证明了该方法的有效性。

人脸识别；Gabor变换；二维非负矩阵分解法

1 引言

人脸识别是通过分析比较人脸特征信息进行身份鉴别的一种计算机技术。随着科学技术的不断发展，生物特征技术尤其是人脸识别技术由于其众多的优越性被广泛应用在很多领域，例如：视频图像监控、身份识别验证、入口控制、刑侦破案等等。

1946年，Gabor把短时傅里叶变换的窗函数取为高斯函数，并提出Gabor变换[1]。Gabor变换具有很强的空间局部性和方向选择性，被广泛应用于人脸识别的特征提取中。传统的Gabor变换对光照和姿态鲁棒性不强，会对识别效果造成影响。1999年，Lee和Seung在《nature》上提出了NMF（非负矩阵分解法）并用于图像处理。NMF算法具有实现上的简便性、分解形式和分解结果上的可解释性，以及占用空间少等优点[2]。但由于NMF矩阵的构建过程中，需对图像进行向量化，会导致部分结构信息丢失，同时，高维数据使得矩阵存在奇异性，分解速度变慢，识别率降低。文献[3]将Gabor变换和NMF方法相结合，对Gabor变换后得到的高维特征，采用NMF方法进行降维，识别效率有所提高，但忽略了Gabor变换易受光照、姿态等外界因素变化的影响，同时在进行NMF分解时并不能保持数据潜在结构，所以识别率并不高。

鉴于上述方法存在的不足，本文采用将改进的Gabor变换与（2D）2NMF（二维非负矩阵分解法）相结合的人脸识别方法。首先对人脸图像进行改进的Gabor变换，提取图像特征，对提取到的高维特征，采用（2D）2NMF（二维非负矩阵分解法）进行降维[4]，进一步提取有效的特征信息，并利用最近邻法进行分类识别。在ORL人脸库上进行实验仿真，实验结果证明该方法识别速度更快，所占的计算存储空间减少，识别效果明显高于传统方法。

2 Gabor变换

Gabor在数字图像分析领域具有很好的性能，Gabor函数可以在空间域和频率域同时进行分析，具有很好的空间局部性和方向选择性[5]。在一定条件下，Gabor变换的多分辨率分析即为Gabor小波变换。由于Gabor变换存在方向性，此时的Gabor小波变换也是具有方向性的小波变换。Gabor变换的本质就是对二维图像求卷积，Gabor变换的效率由二维卷积运算的效率决定。

Gabor滤波器对人脸图像的响应特征主要体现在边缘、位置和亮度三方面，图像的输入信号和Gabor小波的卷积就是卷积的输出结果。当输入信号的变化与小波信号变化一致时，输出比较强。通过修改Gabor函数的参数，可以获得不同中心频率和不同方向上的Gabor滤波器，从而提取到不同局部细节特征和全局性较强的特征，同时能减少噪声干扰。

2.1 传统Gabor滤波器

一个滤波图像包含了图像一个频带和方向上的成分。二维Gabor滤波函数是一个被复正弦函数调制的高斯函数，通常表示为：

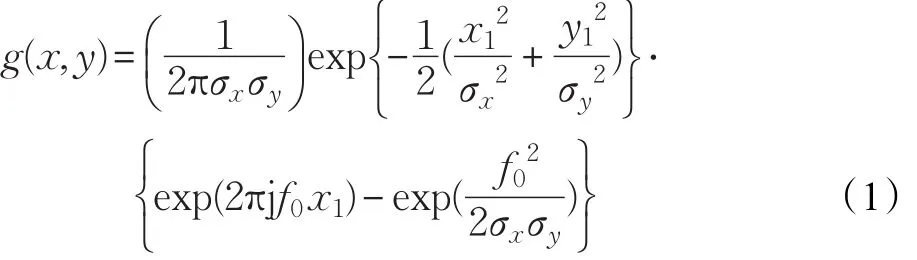
其中，σx和σy是高斯包络在X和Y方向上的标准差，决定了高斯函数在X轴和Y轴上的伸缩程度，f0是中心频率，θ是旋转角。(x,y)是原坐标，(x1,y1)是旋转后的坐标。

x1=xcosθ+ysinθ,y1=-xsinθ+ycosθ，上式中的exp(f20/2σxσy)是直流分量，可以避免Gabor变换对图像绝对亮度的依赖性。

Gabor小波是一组带通滤波器，通过调整各个参数，每一组滤波器都有它们各自的方向和频率选择性，这样，不同频率和方向的滤波器就完全覆盖了整个频率域。一幅人脸图像的Gabor特征也就是该图像与一族Gabor小波的卷积结果。

设一幅图像的灰度分布为I(x,y)，则，它的Gabor特征可表示为如下：

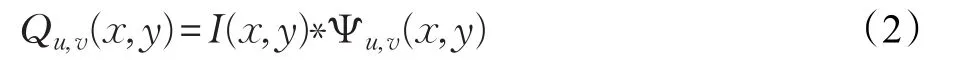
其中，Qu,v(x,y)相当于方向v和尺度u的Gabor卷积结果，Ψu,v(x,y)为Gabor的核函数。当u、v取不同值时就得到了不同方向和不同尺度的Gabor核函数，尺度选的越小得到的图像的细节特征就越多，相反，尺度越大，提取到的大多为图像的轮廓特征。选取的方向越多，覆盖的图像区域面积就越大，得到的图像细节就越多。由于受到很多限制，在进行图像处理时，一般选择一些能够反映图像中大多数特征的方向，这样不但能够减少计算量同时还能提高处理速度。

这里，选取了一个图像进行试验，分别选择0°，45°，90°，135°这4个方向，由于滤波器有对称性，所以在滤波时相当于对8个方向进行了滤波，提高了运算效率，同时选择4个不同尺度，滤波结果如图1。

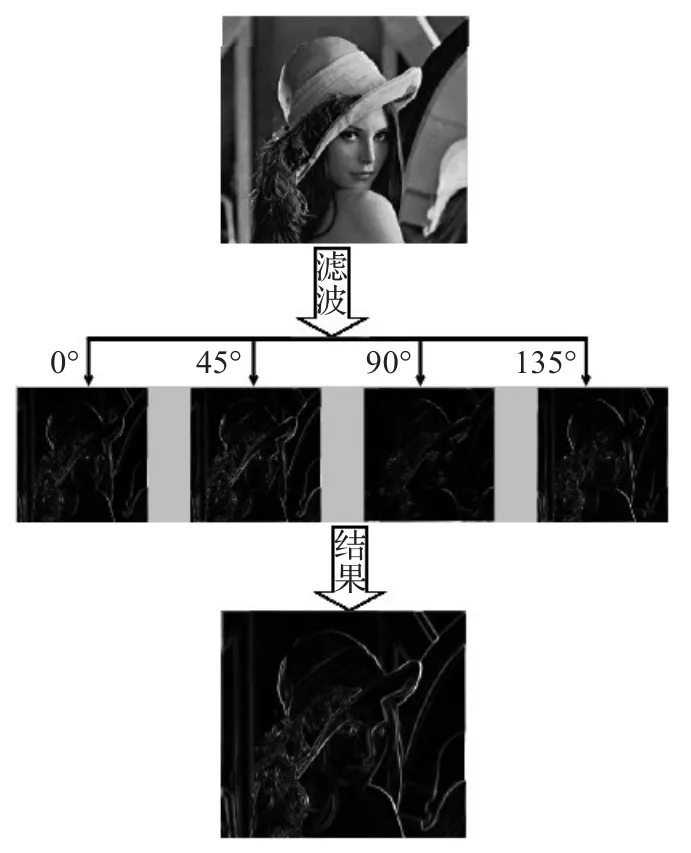
图1 Gabor滤波器滤波图像

实验表明，经过Gabor滤波器滤波的图像，在4个方向都取得了不错的特征。

利用Gabor滤波器提取人脸特征时，由于Gabor特征维数很高，计算量大，实时性差。越来越多的研究人员提出了改进方案，力图在特征的提取准确度与计算效率提高等方面有所突破。

2.2 改进后的Gabor滤波器

在人脸识别中，如何消除光照和姿态变化对人脸识别性能的影响是关键。基于以上Gabor滤波器的性能，对Gabor滤波器做了两点改进：

（1）考虑到直流分量是人脸背景的灰度值，本文补偿了直流分量，以增强Gabor滤波器对全局照明变化的鲁棒性。

如上节所述，传统Gabor变换表达式中，exp(f20/2σxσy)为其直流分量，为了增强Gabor滤波器对光照变换达到鲁棒性，使其具有0直流分量，以保证不同亮度值构成的均匀亮度区域的响应相同。为此，再增加此直流分量，以使直流分量为0，从而实现补偿。

背景灰度值一般是均匀的直流可算作是一个常数用来指代背景，对其进行直流补偿后，背景所受光照，外界干扰影响变小，图像越均匀，图像所处的环境也越好 ，滤波时就会得到很好的效果。

（2）考虑到滤波器具备中心频率越高则相应的脉宽越窄的性能，本文增加一个系数使Gabor滤波器的尺度伸缩随中心频率变化，中心频率高，伸缩尺度小；反之，则伸缩尺度大，使滤波器有较高的品质，可以在一定程度上减少冗余信息[6]。改进后的Gabor滤波函数为：

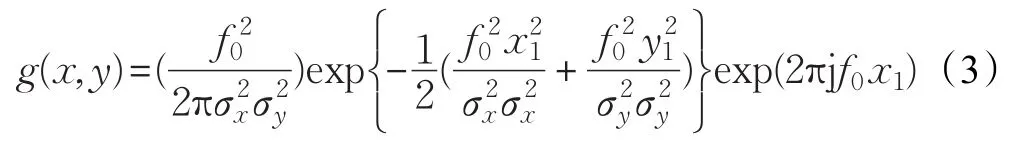
将人脸图像与Gabor滤波器进行卷积，结果就是所提取的图像的Gabor特征。图2是某人脸图像5个尺度8个方向的Gabor幅值特征与相位特征。从图中可以看出，Gabor相位信息随着空间位置呈周期性变化，而幅值的变化相对平滑而稳定。幅值反映了图像的能量谱，Gabor幅值特征通常称为Gabor能量特征，Gabor小波可像放大镜一样放大灰度的变化，人脸的一些关键功能区域（眼睛、鼻子、嘴、眉毛等）的局部特征被强化，从而有利于区分不同的人脸图像。相位信息的周期性变化对光照有一定的不敏感性，受光照变化影响不大。相位特征和幅值特征相比，在光照变化明显的环境下有突出的优势，光照变化越大，Gabor相位特征越有优势。而本文采用的改进的Gabor变换对光照已具有鲁棒性，相位特征优势减弱。相位信息因其为周期性变化的，会一定程度上降低计算效率，因此，本文只应用了Gabor幅值信息，而不应用相位信息。

图2 Gabor的幅值特征与相位特征

3 NMF（非负矩阵分解法）进行特征降维

在对图像进行特征提取过程中，由于提取到的特征太多并且维数较高，会导致图像特征匹配复杂，耗费资源，因此必须对其进行降维。本文采用NMF（非负矩阵分解法）进行特征降维。该方法具有实现上的简便性，分解形式和分解结果上的可解释性，以及占用存储空间少等优点。

3.1 特征降维原理分析

非负矩阵分解利用数据的非负性，用一个包含原始矩阵基本特征信息的低维矩阵来近似表示原始矩阵。对于任意的非负矩阵A，将其分解成一个m×l的非负矩阵W 和一个l×n的非负矩阵 H[7]，通常l远远小于m、n或者l(m+n)＜mn，并且A，W，H 满足下列条件：

其中，W为基矩阵，H为系数矩阵。A中的一列向量为左矩阵W中所有列向量的加权和，权重系数为右矩阵H中对应列向量中的元素。这种基于基向量组合的表示形式即为“局部构成整体”思想。

对上述公式通常利用辅助目标函数来达到解的最优化。优化问题即在WH≥0情况下，寻找使上式达到最小所对应的W和H。可通过乘法迭代算法从任意的非负初始值出发，交替的更新矩阵W和H。目标函数有多种形式，其中矩阵A与WH的欧氏距离的平方最为常用：

对于上式的更新法则：

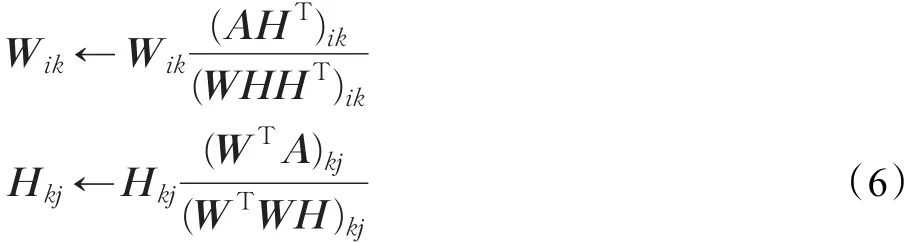
重复上式直至收敛。

3.2 二维NMF（非负矩阵分解法）

传统的NMF分解法在矩阵的构建过程中，图像的向量化会导致部分图像结构信息丢失，对识别效果造成影响。并且没有考虑到所提取的特征和分类目的之间的关系[8]。都会导致其需要更多的计算成本，同时处理图像的效率较低，为此，本文采用（2D）2NMF（二维非负矩阵分解法）进行特征降维。

（2D）2NMF方法是采用二维图像矩阵来构建图像矩阵，分别对原始图像进行行矩阵分解和列矩阵分解[9]。与传统NMF方法相比，能更大程度上减少图像矩阵维数，缩短计算过程所用时间。同时，由于其考虑了图像的结构信息，因而提高了图像的分解精度。

3.2.1 图像矩阵行方向的分解

用矩阵 Xp×qm=[A1,A2,…,Am]表示大小为 p×q的m幅图像，其中Ak代表这M幅人脸图像中的一幅。对其进行NMF分解，得到如下式子：

这里，d为参考维数，L为图像分解后得到的基矩阵，H为系数矩阵。

3.2.2 图像矩阵列方向的分解

用矩阵Yq×pm=[B1,B2,…,Bm]表示大小为 p×q的m幅图像，其中Bk=AkT，表示原图像的转置。对其进行NMF分解，得到如下式子：

这里，r为参考维数，R为图像分解得到的基矩阵，H为系数矩阵。

由于是对图像的行和列分别进行了分解，因此可以提取到图像的二维结构信息。并且信息存储在行基矩阵L和列基矩阵R中。因而，对于任意一幅图像Ak，它在行和列基矩阵上的投影系数可表示为：

利用行基矩阵L和列基矩阵R重构得到的图像可表示为：

3.3 W（基矩阵）和H（系数矩阵）的初始化

对(W,H)进行初始化后，收敛速度显著提高。本文引用基于Lanczos对角化过程去寻找矩阵的一个低秩近似。

Lanczos算法将对称矩阵通过正交相似变换变成对称三对角矩阵的算法[10]。通过Lanczos双对角化先得到矩阵的一个秩K近似，在Lanczos过程中得到每个秩1矩阵的非负部分的近似，最后得到A的非负矩阵分解的初始化矩阵。

Lanczos双对角化过程：

对给定的一个初始化向量b，i=1,2,…,k，计算：

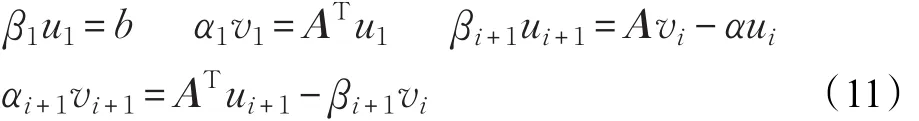
上式的矩阵形式写为：

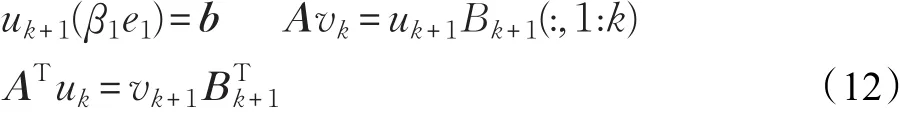
此处Bk+1是一个下双对角矩阵。

主要步骤：

（1）运行K步的Lanczos双对角化过程，得到矩阵JK=UKBKVTK。

（2）从WH=JK-E得到近似的非负矩阵(W,H)。

由于初始向量b的选择不唯一，所以初始化策略带有随机性，但和NMF结合后收敛速度更快。

3.4 NMF方法基个数的确定

基矩阵W的列数即特征基的数量r，直接决定了算法得到的特征子空间的维数。对特定的数据集，隐藏在数据集内部的特征空间的维数是确定的，当r选取与实际数据集的特征空间维数一致时，得到的特征空间以及特征空间的基最有意义[11]，r越小，识别率越低，r越大，识别率越高，当r增大到一定程度时，识别率反而下降。本文采用能量提取法来计算基个数。

对矩阵A进行NMF分解，得到A=WH，目标函数采用：

能量提取法[12]步骤：

（1）计算含有矩阵90%能量的奇异值个数。

（2）将上式 A做奇异值分解，得到分解因子u,s,v,对奇异值 σ1,σ2,…,σk求和，其中k=rank(A)，设基个数为 l，选取90%的能量，r=∑2/∑1＜90% ，(∑2+σr+1)/∑1≥90% ，其中 ∑2=σ1+σ2+…+σr。

若 A为满秩矩阵，当 r＜mn/(m+n)时，l=r；当r≥mn/(m+n)时，令 ∑1=σ1+σ2+…+σk-1，重新利用能量提取法选取90%的能量，确定新的r1，直至r1＜mn/(m+n)，取基个数l=r1。

若A为非满秩矩阵，当r＜mn/(m+n)时，l=max(r,表示正方向取整。

图3是经过NMF分解的重构图像。由图3可看出，经过二维NMF分解后重构图像效果更好。

图3 （a） NMF

图3 （b） （2D）2NMF分解的重构图

4 本文算法步骤

基于改进Gabor变换和二维NMF（非负矩阵分解法）的人脸识别步骤如下：

（1）对训练样本进行图像预处理并采用公式（3）对图像进行Gabor变换。

（2）对Gabor变换得到的特征图像进行（2D）2NMF分解，具体分解过程如上章所述，采用公式（7）～（9）计算得到投影系数，并采用公式（10）计算得出重构图像即低维特征图像。

（3）对测试样本同样进行图像预处理和Gabor变换。

（4）将得到的测试样本的特征图像向训练样本的基矩阵上投影，以此作为测试样本的低维特征图像。

（5）计算出训练样本和测试样本低维特征之间的欧氏距离。

（6）利用最近邻分类器进行分类。

算法流程如图4所示。

图4 算法流程图

5 实验及分析

本文人脸识别算法中，先确定参数。再选用ORL人脸库进行实验，库中共有40个人，每人有10幅，图片灰度级均为256，大小为112×92，并且每幅图像在光照、姿势和角度方面都存在差异。将该人脸图像库分成两组：选取每个人的前五张图像作为训练样本，后五张作为测试样本，这样测试样本和训练样本共有200张人脸图像。

5.1 NMF参数的确定

非负矩阵分解时，有两个因素直接影响识别率，即怎样设置初始矩阵W、H和怎样设置特征子空间的维数。W的列数直接决定了特征子空间的维数，而当特征子空间的维数越大，则会增加计算时间，占用较大的存储空间。只有选取合适的子空间维数，才能使所选取的特征最具代表性和所占用的存储空间最少。为了选择合适的特征子空间维数，采用直方图方法，选取基矩阵每列中的能量占总能量90%以上的信息作为特征信息[11]。经多次实验，特征子空间的维数和识别率的关系如图5所示。

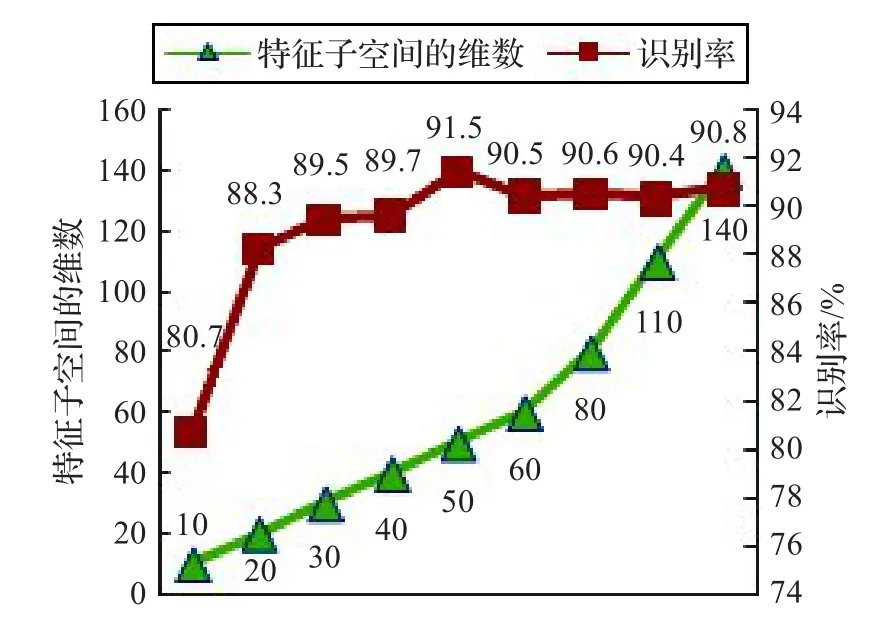
图5 特征空间的维数和识别率的关系

由图5可知当特征子空间的维数达到50时，识别率最高。当特征子空间的维数继续增大时，识别率基本保持不变。与理论相匹配，一个数据结构一定有一个潜在的特征结构，过高或过低的特征维数都会使识别率或计算时间受到影响[13]。

5.2 γ变换因子的选取

图像预处理过程中，将图像经过伽马变换后，图像的对比度会增强，不同的γ值会有不同的变换效果。对于γ值的选取需要通过实验来确定。图6为不同的伽马变换因子测试结果。

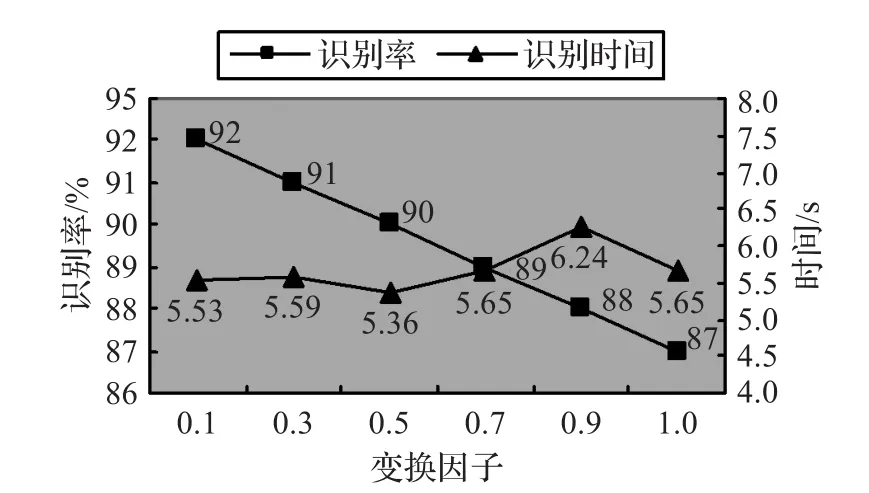
图6 不同的伽马变换因子测试结果

由图可以看出，采用伽马因子γ=0.1，识别率会达到更高，识别时间相对于其他却更少。

5.3 Gabor和改进的Gabor实验比较

图7所示为ORL人脸库中部分具有代表性的人脸图像。

图7 ORL人脸库

对人脸图像分别进行Gabor变换和改进的Gabor变换，所提取的特征图像如图8所示。

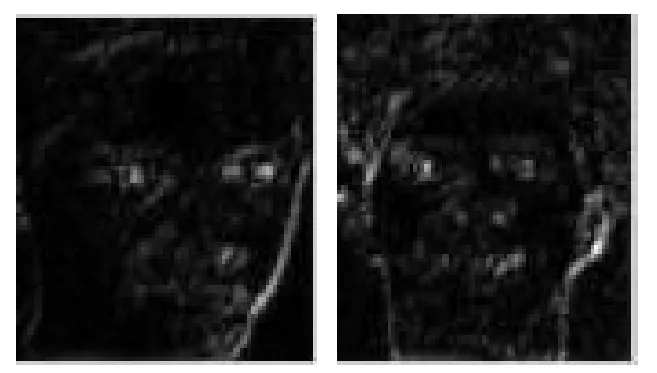
图8 （a） Gabor变换提取的特征图像

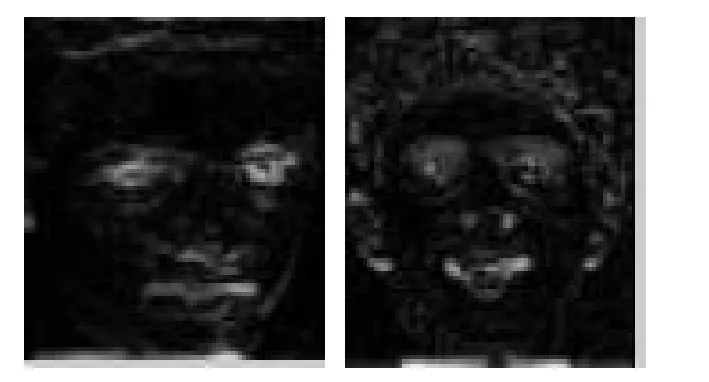
图8 （b） 改进的Gabor变换提取的特征图像

由提取到的特征图像可看出改进的Gabor变换进行特征提取效果更加明显，在特征提取中更具优势。

5.4 NMF和二维NMF实验比较

如图9是NMF和二维NMF在ORL人脸库上进行实验后的比较，由图可看出二维NMF在识别时间和识别精度上都占优势。

5.5 实验结果

为了验证本文方法的有效性，对以下几种人脸识别方法分别进行了实验。第一种，对原图像直接进行Gabor变换提取特征并进行识别；第二种，对原图像直接采用NMF分解进行特征提取并采用K近邻法分类[14]；第三种，对图像进行Gabor变换，对得到的高维特征再进行NMF分解降维，并利用K近邻法分类；第四种，采用改进的Gabor和（2D）2NMF方法提取特征，K近邻法进行分类识别。实验过程中，测试集、训练集、中心频率和方向都相同，在此条件下，不同方法测试结果如表1，识别率为几次测试结果的平均值。

图9 （a） 训练时间比较

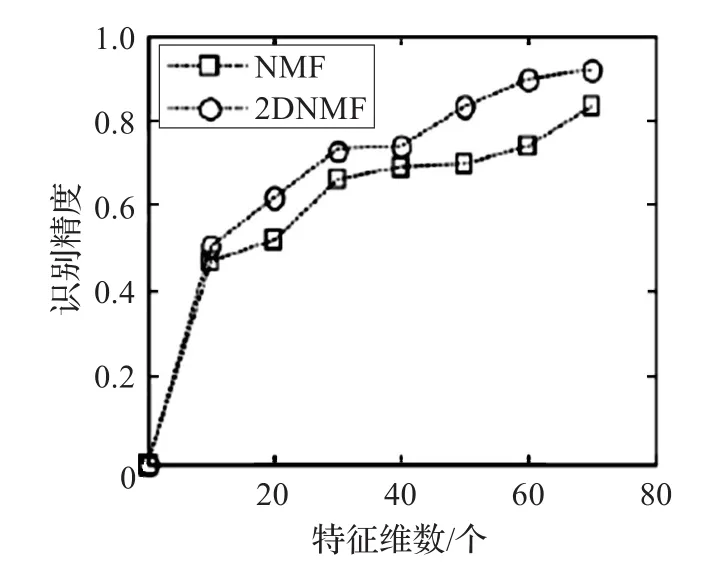
图9 （b） 训练精度比较

表1 不同方法的测试结果

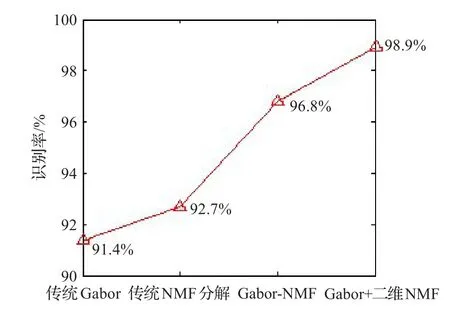
图10 四种人脸识别方法识别率结果图

6 总结

基于传统Gabor变换的识别方法虽然简单高效，但由于其受光照、表情、姿态等变换的影响较为严重，很大程度上降低了识别效率。采用基于传统NMF方法进行人脸识别，由于其在获取子空间的过程中没有利用不同人脸图像的类，所得到的特征不是最佳分类特征，因而容易导致识别错误，降低识别率[15]。将Gabor变换和NMF相结合，明显克服了图像特征维数过高带来的识别率过低问题，提高了识别的精确度，但此方法在利用NMF方法进行特征降维的过程中却很容易造成有用信息的流失，对识别结果造成很大影响。本文采用改进后的Gabor变换来进行特征提取，相比于传统的Gabor变换对光照和姿态等有了更好的鲁棒性，同时减少了信息冗余。对于高维特征，采用（2D）2NMF分解，与传统的NMF方法相比，很大程度上保留了原始图像的结构信息，加快了计算速度，分辨率也大大提高。通过在ORL人脸库进行实验测试，确定了使识别率达到最高的参数，该算法不仅使识别率最大限度的提高，而且保存数据在原始空间几何关系的基础上，使识别率有所提高。

[1]汪堂洪.基于Gabor变换的人脸识别算法研究[D].西安：西安科技大学，2016.

[2]Lee D D，Seung H S.Learning the parts of objects by non-negative matrix factorization[J].Nature，1999，401：788-791.

[3]张素娥，周军，王大伟，等.Gabor小波变换和NMF结合的人脸识别[J].计算机工程与应用，2015，51（3）：1-3.

[4]高宏娟.基于NMF改进算法的人脸识别仿真研究[J].计算机仿真，2011，28（12）：1-2.

[5]李钰，孟祥萍.基于Gabor滤波器的图像特征纹理提取[J].长春工业大学学报，2008，29（1）：2-3.

[6]Lee T S.Image representation using 2D Gabor wavelets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1996，18（10）：859-871.

[7]Chang Y H，Jheng G Y.Customizable facial expression recognition using non-negative matrix factorization[C]//IEEE 2011 International Conferenceon on Electrical and Control Engineering，2011：2073-2084.

[8]高宏娟，潘晨.基于二维NMF及其改进算法的人脸识别[J].计算机应用，2007，27（7）：1-2.

[9]王俊科，左春婷.非负矩阵分解特征提取技术的研究进展[J].自动化，2014，31（4）：973-974.

[10]Simon H D，Zha H.Low-rank matrix approximation using lanczosbidiagonalization processwith applizatins[J].SIAM Journal on Scientific Computing，2000.

[11]王晓华，孙小姣.加权小波和流行正则化的NMF融合的人脸识别[J].计算机工程与应用，2016，52（7）：150-154.

[12]乔涵丽，马昌凤.确定NMF基个数的能量提取法[J].桂林电子科技大学学报，2012，32（6）：487-489.

[13]张志伟，杨帆，夏克文，等.基于小波变换和NMF的人脸识别方法的研究[J].计算机工程，2007，33（6）：176-178.

[14]邱天爽，杨春晖.一种基于改进近邻分类器的人脸识别方法[J].信号处理，2008（1）：54-57.

[15]David G，Jordi V.Non-negative matrix factorization for face recognition[C]//Proceedings of the 5th Catalonian Conference on AI：Topics in Artificial Intelligence，2002，2504：336-344.

WANG Xiaohua,YANG Qingmei,YANG Tao

School of Electronic Information,Xi’an Polytechnic University,Xi’an 710048,China

Face recognition based on improved Gabor transform and nonnegative matrix factorization.Computer Engineering and Applications,2017,53（21）：132-137.

In order to get the high quality facial features and improve the performance of face recognition,the face recognition method based on improved Gabor transform and two-dimensional non negative matrix factorization is proposed in this paper.Improved Gabor transform extracts the characteristics with a higher quality,enhances the robustness.Two dimensional non negative matrix decomposition of dimensionality reduction can greatly reduce the dimension of the image data,shorten the calculation time,improve the recognition rate.At last,experiments are carried in the ORL face database.The results show that improved Gabor transform and two-dimensional NMF method have a slight increase in the calculation time,but the recognition efficiency is improved obviously,thus proves the effectiveness of this method.

face recognition;Gabor transform;two-dimensional non-negative matrix decomposition method

A

TP24

10.3778/j.issn.1002-8331.1607-0226

国家自然科学基金（No.61301276）；西安工程大学控制科学与工程学科建设经费资助（No.107090811）；西安工程大学博士科研启动金项目（No.BS1207）。

王晓华（1972—），女，博士，副教授，研究方向为模式识别、智能机器人等，E-mail：W_xiaohua@126.com；杨清梅（1992—），女，硕士研究生，研究方向为模式识别与智能系统。

2016-07-15

2016-09-12

1002-8331（2017）21-0132-06

CNKI网络优先出版：2017-01-11,http://www.cnki.net/kcms/detail/11.2127.TP.20170111.1014.004.html