一种面向建筑节能的强化学习自适应控制方法

胡龄爻 ，陈建平 ，傅启明 ，4，胡文 ，倪庆文

1.苏州科技大学 电子与信息工程学院，江苏 苏州 215009 2.江苏省建筑智慧节能重点实验室，江苏 苏州 215009 3.苏州市移动网络技术与应用重点实验室，江苏 苏州 215009 4.吉林大学 符号计算与知识工程教育部重点实验室，长春 130012

一种面向建筑节能的强化学习自适应控制方法

胡龄爻1，2，3，陈建平1，2，3，傅启明1，2，3，4，胡文1，2，3，倪庆文1，2，3

1.苏州科技大学 电子与信息工程学院，江苏 苏州 215009 2.江苏省建筑智慧节能重点实验室，江苏 苏州 215009 3.苏州市移动网络技术与应用重点实验室，江苏 苏州 215009 4.吉林大学 符号计算与知识工程教育部重点实验室，长春 130012

针对建筑节能领域中传统控制方法对于建筑物相关设备控制存在收敛速度慢、不稳定等问题，结合强化学习中经典的Q学习方法，提出一种强化学习自适应控制方法——RLAC。该方法通过对建筑物内能耗交换机制进行建模，结合Q学习方法，求解最优值函数，进一步得出最优控制策略，确保在不降低建筑物人体舒适度的情况下，达到建筑节能的目的。将所提出的RLAC与On/Off以及Fuzzy-PD方法用于模拟建筑物能耗问题进行对比实验，实验结果表明，RLAC具有较快的收敛速度以及较好的收敛精度。

强化学习；马尔科夫决策过程；Q学习；建筑节能；自适应控制

1 引言

纵观近几十年建筑领域的发展，建筑结构设计与设备管理方面，特别是涉及到生态控制和能源消耗的领域上，都有很显著的进步和变化。一个明显的转折点是在20世纪70年代石油危机爆发之后，提出封闭的建筑物以最小化建筑物的能源消耗这一概念，但是这导致室内空气质量直线下降和全世界范围的健康问题。这就直接造成了研究确保人类舒适度的前提下，同时联系光照、温湿度和空气质量等其他因素的研究趋势。

在现有的能耗研究中，建筑物能耗占世界范围内总基础能耗的45%，这是在总能源消耗中占比例最高的一项。全球范围的建筑能耗，包括民用住宅和商业建筑，在发达国家每年的增长速率已达到20%～40%。然而在一项调查中，商业建筑物的年均耗能大约是70～300 kWh/m2，这个数据是民用住宅的10到20倍。人口的增长、建筑服务压力的提升和舒适标准的提高都增大了建筑物的能源消耗，这些预示着未来仍然会持续能源需求的增长趋势。正是因为上述原因，建筑节能已然成为当今所有国家和国际水平在能源政策上重视的首要目标。建筑物的能源消耗问题已经得到越来越多的关注，毕竟建筑物是与人类生活工作息息相关的，也是现代化发展中必不可少的一个环节。

控制器是实现建筑节能必不可少的重要组成部分。神经网络、模糊系统、预测控制和它们之间的组合是现有在建筑领域的主流控制器研发的方向[1-4]。Dounis等人提出一种Fuzzy-PD方法的控制器，用模糊的比例微分方法来控制建筑领域内的相关设备[2]。然而在智能控制算法上应用广泛的是强化学习和深度学习[5]，有许多学者将强化学习的方法应用在能耗预测或控制领域上[6-11]。其中较为典型的是Dalamagkidis等人于2007年提出的一种线性强化学习控制器——LRLC（Linear Reinforcement Learning Controller）[6]，主要是用基于强化学习的时间差分方法（Temporal-Difference，TD）的算法，进行能耗监测和策略决策。LRLC与传统的On/Off控制器和Fuzzy-PD控制器相比较，在监测能耗和控制稳定性上有更好的表现，但是由于其算法要求有足够的探索过程，在真实的建筑物中，抽出一个很小的时间让控制器去选择随机的动作是不可能实现的。因为即使选择的动作是接近最优动作的，这也会导致用户不满度或者整体能源消耗临时增加。在实际中出现的问题有：在冬天（或夏天）的时候控制器会允许开冷气（或暖气）。在此之后，Dalamagkidis等人还提出了一种基于RLS-TD（recursive least-squares algorithm）递归最小二乘算法的强化学习控制器[12]，其实验结果表明与之前的方法比较有进一步的提升。

由于传统的方法如Fuzzy-PD[13-14]，控制建筑领域内的相关设备，有收敛速度慢和稳定性差的缺点，于是提出一种强化学习自适应控制方法RLAC（Reinforcement Learning Adaptive Control）。RLAC采用Q学习算法对空调系统和通风系统等建筑内设备进行控制，通过状态s得到r值进而得到Q值，从Q值中得到的策略选择动作a，采取动作之后更新s，一直重复更新至终止时间步。RLAC与LRLC的差异在于：LRLC是需要确切模型的，而RLAC是不需要模型的，在与环境的交互中可最终收敛到最优策略。进行几组对比实验结果表明，RLAC方法具有有效的节能性；RLAC在不同初始状态设置下均能达到良好的收敛速度和精度；与Fuzzy-PD方法和On/Off方法相比较，有更快的收敛速度，收敛之后更加稳定。

2 相关理论

一个强化学习任务可以被建模为马尔可夫决策过程（Markov Decision Process，MDP），其中环境的状态只取决于当前状态和选择的动作，因此可以利用现有的信息去预测未来的状态和该状态的期望回报。此时奖赏值函数只取决于当前状态和动作，与其他历史状态和动作无关。MDP一般可以表示为一个四元组(S,A,T,R)，其中S表示所有环境状态s构成的状态空间，状态s可由多个变量构成；A表示学习器（Agent）所能执行的所有动作a构成的集合；T:S×A×S→[ ]0,1为环境状态迁移概率函数，T(s,a,s′)表示Agent在状态s中执行动作a后环境迁移到新状态s′的概率；R:S×A×S→ℝ为奖赏函数，R(s,a,s′)表示Agent在环境状态s中执行动作a且环境迁移到状态s′所能得到的立即奖赏，一般也用r表示。

策略（policy）定义了强化学习Agent的行为方式，简单地说，策略就是从环境感知的状态到可采用动作的一个映射。策略分为确定策略和随机策略，确定策略是从状态到动作的映射；随机策略是从状态动作对到概率的映射。因此，强化学习的目标是学习一个最优策略，该最优策略能够获得最大的期望累积奖赏，通常也被称为回报，如式（1）所示：

其中γ是一个0≤γ≤1的参数，被称为折扣率。γ越小，就表示Agent越关心长期奖赏。值函数是关于回报的期望，因此，强化学习问题也可以转换为求解最优值函数的问题。值函数分为动作值函数Q(s,a)和状态值函数V(s)，其中状态值函数V(s)用来表示状态的好坏，动作值函数Q(s,a)用于表示动作状态对的好坏。Q(s,a)与V(s)的更新公式如式（3）和式（4），其中 α在强化学习中被称为学习率，其取值范围是（0，1]。

很多强化学习问题是一个没有终止状态的问题，因此，回报值也会趋于无穷大。为了解决这个问题，强化学习中给出折扣回报的定义，公式如下：

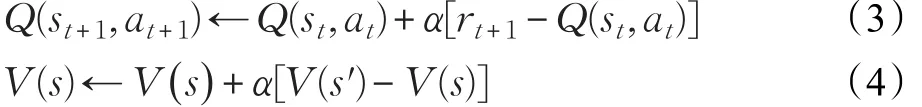
强化学习方法可基本分为三类，每一种都有其适用范围和优缺点，按照是否需要模型分为需要模型的动态规划方法（Dynamic Programming，DP），以及不需要模型的蒙特卡罗方法（Monte-Carlo，MC）和时间差分方法（Temporal-Difference，TD）。MC和TD的区别在于MC需要走完一个情节到终止状态再估计值函数，而TD则不需要完整的情节样本。本文用的是时间差分的学习方法中的Q学习算法，是一种异策略（off-policy）的TD控制算法。在不依赖策略的情况下，Q学习学到的动作值函数Q会直接逼近最优动作值函数。Q学习的Q值更新公式为[15]：

3 强化学习自适应控制方法

3.1 算法框架建模

RLAC采用Q学习算法，状态s是二氧化碳浓度、室内温度和设置温度的矩阵表示，动作a是空调系统动作、开窗动作和通风系统动作的排列组合，达到室内温度稳定在设定温度、通风并减少能耗的效果。

3.1.1 环境建模

对于Agent而言，外部环境是一个封闭性房间，需要的参数是房间内的温度Tt（单位是摄氏度），室内CO2浓度ρt（单位为10-6）以及设置温度setT（单位是℃），这三个参数构成了RLAC中的状态s。根据实际情况，设置室内温度Tt的范围为[0，40]，ρt的范围为[200，1 000]，实际情况的温度和CO2浓度一定是处于这个范围内的。CO2浓度的作用是：当CO2浓度低至300×10-6时给一个接近于0的值；当该浓度高于850×10-6时给一个接近于1的值。这里设置的300×10-6是室外CO2浓度能达到的最低水平，而850×10-6则是室内人体感觉舒适的最高水平。在开启空调系统的同时，采取通风系统和开窗动作，会一定程度上减弱空调系统的作用，本文模型设定减弱参数为0.2。模型中CO2浓度与开窗动作和通风系统有关，影响因子比例设为1∶2。

3.1.2 算法框架设计

RLAC中全部动作建模为64×3的矩阵，action_num=64，其横向量是一个三维的向量，表示一个动作。动作向量第一位kongtiao_fig表示空调系统动作：1表示取暖小风，2表示制冷小风，3表示取暖大风，4表示制冷大风；第二位windows_fig表示开窗状态：0为关闭，1为微张，2为半张，3为全开；最后一位tongfeng_fig表示通风系统动作：0是关闭，1是小档，2是中档，3是大档。

RLAC中状态s=[Tt,ρt,setT]由房间内的温度Tt，室内二氧化碳浓度ρt，以及空调设置温度setT几个参数构成，其计算公式如式（7）～（9）所示。状态中附加的一个参数是实时能耗Et，其中T0是室内初始温度，Emax是一个片段的空调系统、电动开窗系统和通风系统的最大总能耗值，这个值通常是由经验获得，可以从空调与通风系统设备的操作特性和它的近期操作设置中得到。T_penalty是室内温度参数；indoor_air_quality_penalty是室内空气质量参数；E_penalty是能耗参数。

奖赏被建模为在区间[-1，0]中可取任何值的变量，这个变量是作为一个惩罚值，也就是说在能源消耗非常高或者二氧化碳浓度很高时，这个变量值很小（接近于-1），反之这个变量值将很大（接近于0），其计算如式（6）所示。w1、w2、w3分别是其权重参数，室内温度稳定在设置温度是首要目的，同样也要考虑CO2浓度和能耗因素，经过多次实验效果对比，RLAC模型中参数的设置为：w1=0.7，w2=0.25，w3=0.05。这样能保证最终r值在在区间[-1，0]内，并且整个系统保持良好的性能表现。

RLAC中状态转移公式如式（10）～（13）所示，其中T_changerate表示温度变化速率，与采取动作是大风还是小风有关，其公式如式（12）所示。

r值作为模型最终评价标准，是室内温度参数、室内空气质量参数与能耗参数的加权值，设置r为一个负值，如公式（6）所示，当三个相关参数越小时，r的值就越大，模型需要的就是尽可能大的r值。也就是说，当室内温度越接近设置温度，室内CO2浓度越低，能耗值越低时，模型获得的r值就越大，这也就是控制器要达到的最终目的——在不影响人的舒适度的条件下达到节能的目的。

3.2 控制算法

（9）直到s是终止状态。

算法1主要借鉴Q学习的主要思想，在状态s下采取动作a之后更新r值，利用Q中得到的策略选择a并采取动作，之后进一步更新r和s。每一个时间步都采取动作并更新状态和r值来改变策略，最终收敛于最优策略。

RLAC方法的具体算法，见算法1：

算法1 RLAC

（1）初始化r=0，a为64×3的矩阵。

（2）重复（对于每个片段）。

（3）初始化 s0(T0,ρ0,setT)。

（4）重复（对片段的每个时间步）。

（5）根据r的值选择一个动作a，并采取这个动作。

（6）根据公式（10）～（13）进行状态转移 s←s'。

（7）根据公式（6）～（9）更新 r值。

（8）根据公式（5）更新Q 值。

4 实验结果与分析

为了验证RLAC模型的有效性，将仿真实验在Pytho2.7环境中进行，采用的编辑器为Sublime Text3。下列实验均设置每个情节最大步数为5 000步，一共160个情节共800 000步。

4.1 RLAC的仿真步骤

RLAC的仿真步骤如下：

步骤1 建立状态变迁模型（如式（10）～（13）、奖惩反馈模型（如式（6）～（9）和评价行为值函数 Q(st,at)（如式（5））。

步骤2初始化评价行为值函数Q(st,at)、学习率α，折扣率γ，其中，s表示状态因素，a表示行为因素，γ是一个0≤γ≤1的参数，状态因素是由室内温度Tt、室内二氧化碳浓度ρt、实时能耗Et和空调设置温度setT构成，行为因素是由空调系统行为、电动开窗系统行为和通风系统行为构成。

步骤3运行片段，每个片段包括N个单位时间步，令时刻t=0，初始化初始状态因素s0，也就是确定0时刻的T0、ρ0、E0=0和 setT 。

步骤3.1每个单位时间步的运行包括：对当前状态因素st，根据贪心选择策略h(st)计算确定出当前状态因素st在时刻t的行为因素at，a∈h(st)。

采取这个行为因素at，根据建立的状态变迁模型计算状态因素的变迁，状态因素变迁到下一状态因素st+1。

根据建立的奖惩反馈模型计算得出在状态因素st和行为因素at下的奖惩rt。

更新（如式（5））当前评价行为值函数Q(st,at)。

更新学习率α，t=t+1。

步骤4进行判断，具体为：

若st+1对应的状态不符合状态结束条件，则返回到步骤3.1，进行下一单位时间步的运行。

若st+1对应的状态符合状态结束条件，则监测所有状态因素下的评价行为值函数是否满足预定的精度要求，若有评价行为值函数不满足精度要求，则返回到步骤3进行新的片段的运行，若评价行为值函数都满足精度要求，则结束循环。

步骤4中，若st+1对应的状态不符合状态结束条件是指：若st+1对应的单位时间步的步数小于循环设置的最大步数N；若st+1对应的状态符合状态结束条件是指：若st+1对应的单位时间步的步数等于循环设置的最大步数N。当然，状态结束条件也可以设置为其他的状态因素结束条件。

4.2 RLAC的仿真实验结果

（1）关于模型的节能性的对比实验

如表1所示，实验1.1，1.2为一组，初始状态都是s0=[8,850,30]，其奖赏函数r的权重参数不同，实验1.1设置为 w=[0.7,0.25,0.05]，实验1.2设置为 w=[0.7,0.3,0]，其区别在于实验1.1的奖赏函数中考虑了能耗参数，而实验1.2的奖赏函数中未考虑能耗参数。实验1.3，1.4为一组，初始状态都是s0=[30,770,20]，这两个实验区别也是在奖赏函数的权重参数设置上，与上一组实验设置相同。实验结果表明，是否考虑能耗参数并未影响实验的收敛速度和收敛效果，只在总能耗值和平均能耗上产生差异。如表1所示，虽然在实验收敛前，实验1.1比实验1.2的平均能耗分别高出430左右，但在实验数据收敛之后，其平均能耗比实验1.2的数据低了1 000左右，从长远节能的方面考虑，考虑节能因素的实验1.1比较未考虑节能因素的实验1.2更符合节能的目的。实验1.3与实验1.4的实验数据更能说明这一点，实验1.3在收敛前后的平均能耗比实验1.4分别低了2 000和4 300左右，表明考虑节能因素在内的奖赏函数使整个系统更节能。

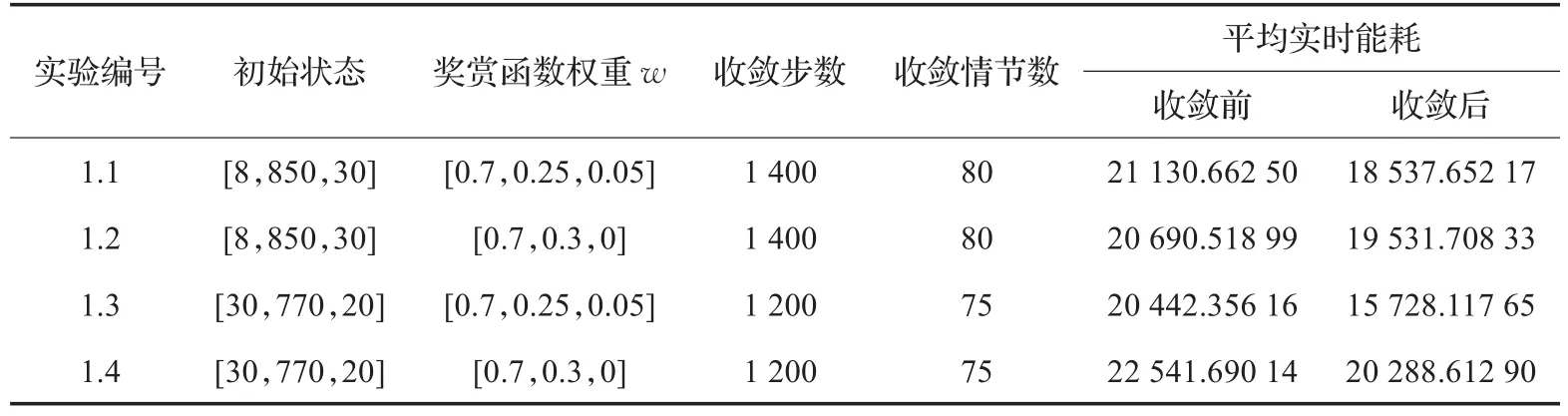
表1 实验1中四组子实验各参数表

接下来的所有实验均考虑能耗参数，即奖赏函数权重值w=[0.7,0.25,0.05]。

（2）关于RLAC方法收敛性能的对比实验

实验2.1的初始状态为s0=[30,770,26]，实验2.2的初始状态为s0=[16,770,26]，实验2.3的初始状态为s0=[30,850,20]，实验2.4的初始状态为s0=[8,850,30]。实验数据如图1至图4所示。

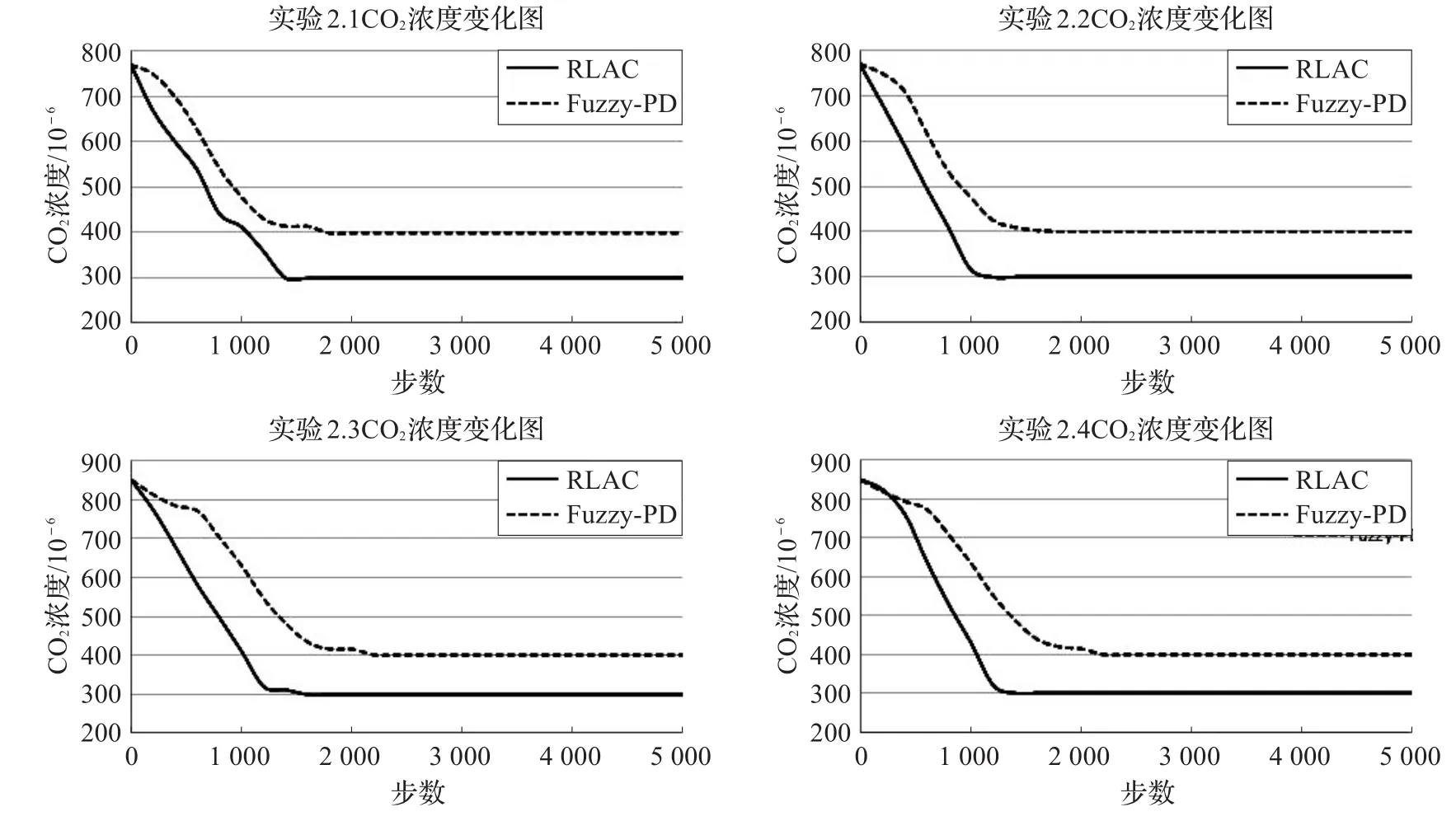
图1 实验2收敛后CO2浓度变化

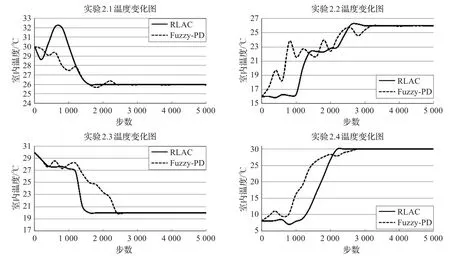
图2 实验2收敛之后温度变化图

图1 是实验2四组子实验收敛之后CO2浓度的变化图，由图可知RLAC方法与实验2.1在1 400步左右达到最低浓度300×10-6，并保持良好的稳定性；而实验2.2、实验2.3和实验2.4则在1 200、1 600和1 400步左右达到一样的效果。相比较而言，Fuzzy-PD方法表现不如RLAC方法，在四组实验中分别在1 400、1 500、2 000和2 200步左右达到最低400×10-6左右。实验表明，RLAC能在更短时间步内达到更好的通风效果，以保证良好的室内空气质量。

图2是实验2中四组子实验收敛之后室内温度的变化图，由图可知两种方法均可达到设置温度并保持稳定，其差别在于收敛速度不同：RLAC在四组子实验中分别在1 600、2 600、1 600和2 200步左右达到收敛；而Fuzzy-PD方法则需要2 600、3 500、2 400和2 800步。实验表明，RLAC方法比较Fuzzy-PD方法能在更短的时间步内达到设置温度，并保持良好的稳定性，保证室内良好舒适的热环境。

图3是实验2在实验过程中的总回报收敛图，如图所示实验2.1每个情节总回报在前20个情节内RLAC回报处在震荡非常大的阶段，振幅一度超过6 000，但在20～80个情节内振幅保持在4 000以内，此时的震荡幅度还是比较大；400 000步即80个情节左右收敛在-2 000左右，振幅不超过1 000。实验2.2、实验2.3和实验2.4的总回报则分别在100、108和122个情节收敛到-4 500、-5 000和-13 000左右。

图4是实验2在160个情节内的每个情节所需收敛步数图，如图所示：实验2.1在实验刚刚开始几个情节并未收敛，所以显示的收敛步数是最大值5 000步；在60个情节之前收敛步数很不稳定，震荡幅度很大，这个时间段RLAC处于学习阶段；而在60～80个情节内，系统达到有微振幅的阶段，此时系统在调整策略；最终在80个情节之后基本收敛在1 400步左右，系统达到稳定最优策略。实验2.2、实验2.3和实验2.4则分别在100、100和120个情节之后达到1 500步左右并保持稳定。

图3 实验2总回报收敛图

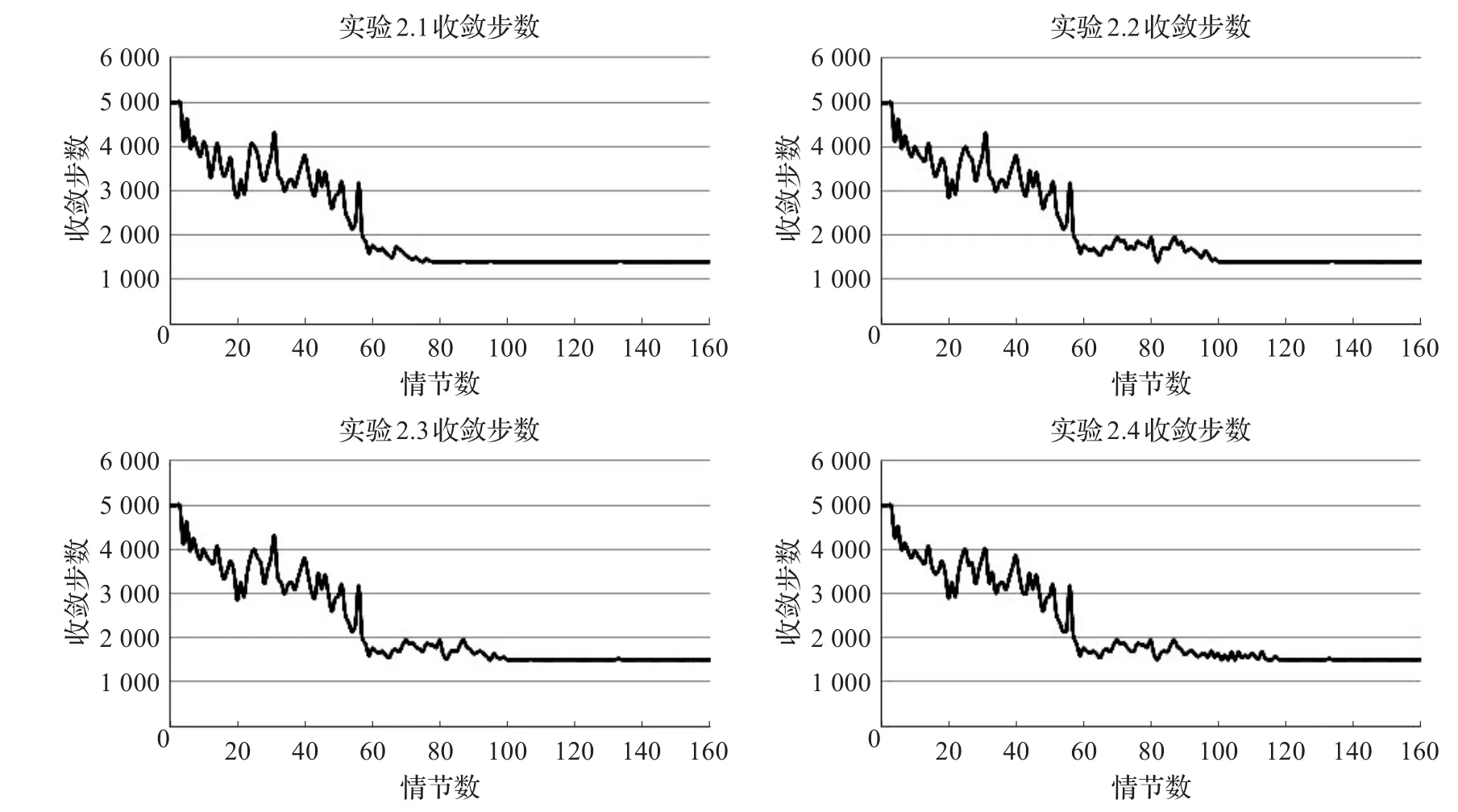
图4 实验2收敛步数图

（3）关于RLAC方法对建筑物内相关设备控制性能的实验

本实验主要是将RLAC方法与Fuzzy-PD方法和On/Off方法进行对比实验。

图5是设置初始状态为s0=[30,850,26]的情况下，总回报与情节数的收敛情况，该图数据为20次实验数据取平均得到。实验中设置一共有160个情节，每个情节是5 000步，总步数为800 000步。

图5 实验3总回报收敛图

由图5可看出，RLAC模型在实验开始阶段表现很不稳定，每个情节的总回报值上下波动超过了±2 000，平均到每一步的奖赏波动超过±0.4，这是因为这个阶段是Agent刚开始学习的阶段，采取试错的方法在探索与利用之间找到平衡。经过约30个情节训练与学习，RLAC模型的总回报值波动值缩小到±500左右，平均到每一步的奖赏波动幅度约为±0.1；最后模型经过60个情节之后基本收敛，每个情节的总回报值上下波动不超过±70，平均到每一步的奖赏上下波动不超过±0.014，基本可以确定模型收敛。可以从图中看到，RLAC模型Agent的学习速率是很快的，基本在300 000步（60个情节）就能收敛，总的实验时间为0∶34∶57，收敛时间约为0∶13∶00。

图6是RLAC在每一个情节内达到收敛所需步数，由图中可看出：实验设置每个情节为5 000步，刚开始实验模型不能在5 000步内收敛；0～50个情节内收敛步数一直在2 500～4 400步的范围里震荡，这个阶段是Agent的学习阶段；50个情节之后收敛步数有个明显下降的趋势，直到60个情节基本稳定收敛在1 400步，说明在60个情节之后Agent找到了最优策略，使得系统在之后的每个情节内都能在14 00步左右达到稳定。

图6 实验3每个情节的收敛步数

图7 是在每个情节总回报值基本收敛之后，随机取出其中一个情节，在5 000步内室内温度T的变化情况，每200步采样一次。由图可知，0～1 400步阶段，RLAC模型Agent在探索学习阶段，温度变化很不稳定。但在1 400步之后本文模型基本稳定，室内温度T保持在设置温度26℃左右。由此可得出结论，RLAC模型Agent可满足空调系统维持室内温度等于设置温度的要求。Fuzzy-PD方法在2 000步左右才收敛到设置温度26℃，On/Off方法则需要在2 600步之后才能收敛。由图7可得出，RLAC采用强化学习方法比传统Fuzzy-PD方法和On/Off方法效果更好，在更少的步数内就能收敛达到稳定。

图7 实验3情节收敛后室内温度变化图

图8 是在每个情节总回报值基本收敛之后，随机取出其中一个情节，每200步采样一次，在5 000步内室内CO2浓度的变化情况。由图可知，0～1 200步阶段，RLAC模型Agent在探索学习阶段，CO2浓度没有达到要求的低于450×10-6。但在1 200步之后本文模型基本稳定，室内CO2浓度保持在与室外CO2浓度380×10-6左右。而Fuzzy-PD方法在1 800步之后才到达稳定值400，；On/Off方法要经过2 400步的学习才达到收敛，收敛于485左右。由图8可知RLAC模型可以满足室内通风的效果，比另外两个方法在更少的步数内收敛，并且CO2浓度稳定值最低，通风效果最好。

图8 实验3情节收敛后CO2浓度变化图

5 结束语

针对传统控制方法对于建筑物通风与空调系统控制存在收敛速度慢、不稳定等问题，提出一个基于强化学习的动态自适应控制模型RLAC，RLAC采用Q学习算法，对真实房屋空调系统与通风系统进行模型构造，并将节能因素考虑在内。RLAC输入为CO2浓度、室内温度和设置温度三个状态的矩阵表示，输出是空调系统动作、开窗动作和通风系统动作的排列组合，目的是在保证达到设置温度和CO2浓度的基础上达到节能的效果。实验中设置一共有160个情节，每个情节是5 000步，通过160个情节的实验，并将RLAC数据与Fuzzy-PD方法和On/Off方法的实验数据进行对比实验。实验结果表明：（1）RLAC方法具有有效的节能性；（2）RLAC在不同设置参数下均能达到良好的收敛性和稳定性；（3）强化学习的算法思想用于建筑物空调与通风系统的控制领域，对比Fuzzy-PD和On/Off两种方法RLAC有更好的收敛性和鲁棒性。

[1]Dounis A I，Santamouris M J，Lefas C C，et al.Thermal comfort degradation by a visual comfort fuzzy reasoning machineunder natural ventilation[J].Journal of Applied Energy，1994，48（2）：115-130.

[2]Dounis A I，Santamouris M J，Lefas C C，et al.Design of a fuzzyset environmentcomfort system[J].Energy and Buildings，1995，22（1）：81-87.

[3]Dounis A I，Bruant M，Guarracino G，et al.Indoor air quality control by a fuzzy reasoning machine in naturallyventilated buildings[J].Journal of Applied Energy，1996，54（1）：11-28.

[4]Clarke J A，Cockroft J，Conner S，et al.Simulation-assisted control in building energy management systems[J].Energy and Buildings，2002，34（9）：933-940.

[5]Mnih V，Kavukcuoglu K，Silver D，et al.Playing atari with deep reinforcement learning[C]//NIPS Deep Learning Workshop，2013.

[6]Dalamagkidis K，Kolokotsa D，Kalaitzakis K，et al.Reinforcement learning for energy conservation and comfort in buildings[J].Building and Environment，2007，42（7）：2686-2698.

[7]Mocanu E，Nguyen P H，King W L，et al.Unsupervised energy prediction in a smart grid context using reinforcement cross-building transfer learning[J].Energy and Buildings，2016，116：646-655.

[8]Shaikh P H，Nor N B M，Nallagownden P，et al.A review on optimized control systems for building energy and comfort management of smart sustainable buildings[J].Renewable and Sustainable Energy Reviews，2014，34：409-429.

[9]Whiffen T R，Naylor S，Hill J，et al.A concept review of power line communication in building energy management systems for the small to medium sized nondomestic built environment[J].Renewable and Sustainable Energy Reviews，2016，64：618-633.

[10]Hazyuk I，Ghiaus C，Penhouet D.Model predictive control of thermal comfort as a benchmark for controller performance[J].Automation in Construction，2014，43：98-109.

[11]Yang L，Nagy Z，Goffin P，et al.Reinforcement learning for optimal control of low exergy buildings[J].Applied Energy，2015，156：577-586.

[12]Dalamagkidis K，Kolokotsa D.Reinforcement learning for building environment control[M].[S.l.]：INTECH Open Access Publisher，2008：283-294.

[13]Egilegor B，Uribe J P，Arregi G，et al.A fuzzy control adapted by a neural network to maintain a dwelling within thermal comfort[C]//Proceedings of Building Simulation，1997，97：87-94.

[14]Ulpiani G，Borgognoni M，Romagnoli A，et al.Comparing the performance of on/off，PID and fuzzy controllers applied to the heating system of an energy-efficient building[J].Energy and Buildings，2016，116：1-17.

[15]Sutton R S，Barto A G.Reinforcement learning：An introduction[M].Cambridge：MIT Press，1998.

HU Lingyao1，2，3,CHEN Jianping1，2，3,FU Qiming1，2，3，4,HU Wen1，2，3,NI Qingwen1，2，3

1.College of Electronics and Information Engineering,Suzhou University of Science and Technology,Suzhou,Jiangsu 215009,China 2.Jiangsu Province Key Laboratory of Intelligent Building Energy Efficiency,Suzhou,Jiangsu 215009,China 3.Suzhou Key Laboratory of Mobile Network Technology and Application,Suzhou,Jiangsu 215009,China 4.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun 130012,China

Building energy efficiency oriented reinforcement learning adaptive control method.Computer Engineering and Applications,2017,53（21）：239-246.

With respect to the problem of slow convergence and instability for the traditional methods,in the field of building energy efficiency,this paper proposes a new reinforcement learning adaptive control method,RLAC by combining Q-learning.The proposed method models the exchange mechanism of the building energy consumption,and tries to find the better control policy by solving the optimal value function.Furthermore,RLAC can decrease the energy consumption without losing the performance of good comfort of the building occupants.Compared with the On/Off and Fuzzy-PD,the proposed RLAC has a better convergence performance in speed and accuracy.

reinforcement learning;Markov Decision Process(MDP);Q-learning;building energy efficiency;adaptive control

A

TP181

10.3778/j.issn.1002-8331.1702-0217

国家自然科学基金（No.61502329，No.61602334，No.61672371）；住房与城乡建设部科学技术项目（No.2015-K1-047）；江苏省自然科学基金（No.BK20140283）；苏州市体育局体育科研局管课题（No.TY2015-301）；苏州市科技计划项目（No.SYG201255，No.SZS201304）。

胡龄爻（1994—），女，硕士，主要研究领域为强化学习、建筑节能；陈建平（1963—），男，教授，硕士生导师，主要研究领域为建筑节能、智能信息处理；傅启明（1985—），男，讲师，中国计算机学会会员，主要研究领域为强化学习、模式识别、建筑节能，E-mail：fqm_1@126.com；胡文（1992—），女，硕士，主要研究领域为强化学习、建筑节能；倪庆文（1993—），女，硕士，主要研究领域为建筑节能。

2017-02-22

2017-05-03

1002-8331（2017）21-0239-08