不确定环境下码头堆场设备集成调度优化

卢毅勤

上海电力学院 经济与管理学院，上海 200090

不确定环境下码头堆场设备集成调度优化

卢毅勤

上海电力学院 经济与管理学院，上海 200090

集装箱码头堆场设备调度优化中，对确定条件下的内集卡和场桥的联合调度研究较多，且没有考虑外集卡的随机到达情况。考虑内集卡和场桥作业过程中的不确定性因素，包括：内集卡行驶速度，场桥行走速度和作业时间，并考虑外集卡随机到达堆场对于内集卡调度作业的影响，构建了不确定因素条件下的堆场设备集成调度优化模型，其优化目标是在考虑外集卡随机到达的情况下，最优化堆场设备的作业时间。设计了求解模型的粒子群算法，并比较了一般确定性模型和考虑不确定因素优化模型的结果。算例结果表明，所建立的模型和算法能有效真实地反映不确定因素对集装箱码头堆场设备作业的影响。

不确定因素；集成调度；堆场设备；外集卡

1 引言

集装箱堆场作为衔接海运和内陆系统的缓冲区域，对于减少船舶装卸时间从而提高整个港口的作业效率和竞争力都有着非常重要的意义。堆场设备调度主要包括场桥调度和内集卡调度问题，主要是对既定作业区内，在任务与堆场设备数量一定的情况下，对场桥和集卡进行作业任务的分配，使作业时间最短。杨朋[1]建立了同时考虑货位分配和拣选路径的集成优化模型，缩短了集卡装卸任务最小化单位指令周期的行程时间。赵宁[2]研究集卡的利用率，建立集装箱港口发箱任务的集卡指派模型。Kim[3]等考虑场桥操作的不同限制条件，建立混合整数规划模型，采用基于分支界定法和贪婪随机适应搜索过程的算法求解。Ng等[4-5]研究场桥优化调度问题，以等待时间最小化为目标建立模型并用分支界定法求解。韩晓龙[6]通过建立两阶段规划模型求解了场桥调度问题。

在场桥与集卡集成调度研究中，Cao等[7]以出口箱集卡和场桥同步化作业的完工时间最小化为目标，建立混合整数模型。乐美龙[8]构建了场桥与集卡的协调调度模型，目标是使所有作业总完工时间最短。但以上研究都是在确定情况下进行的，目前国内外对于不确定情况下堆场优化调度研究比较有限。刘艳等[9]针对进箱时间的不确定性，应用模糊机会约束规划方法平衡各箱区作业量，并以箱区作业量为约束条件，最小化集卡的行驶距离和同组进口箱所占箱区的数量，建立箱位分配模糊优化模型。周鹏飞[10]考虑了集装箱进出场时间的随机不确定性,建立了出口箱位随机规划模型。但以上不确定性研究仅仅针对堆场箱位分配问题，不确定情况下堆场内的设备调度优化问题仍然没有得到解决。此外，以上研究均没有考虑外集卡随机到达对内集卡调度作业的影响。目前我国码头广泛采用的作业模式是内、外集卡作业互不干扰，即外集卡要等待场桥对内集卡全部服务完成以后，才能被空闲的场桥服务。这样，虽然保证了堆场内作业以最快速度完成，但是忽略了外集卡在堆场外的等待时间。对于码头的服务对象（如船舶公司）的成本会产生影响，可能导致码头业务的流失。

因此，本文综合考虑外集卡等待时间和堆场内集卡作业完成效率，统筹安排堆场设备作业顺序，从而让堆场设备在尽可能短的时间内既完成对内集卡的装卸服务，又能提升码头对外集卡的服务能力，提高码头服务质量，吸引更多业务。本文引入内集卡运行速度、场桥作业时间及行走速度这三大重要不确定性因素，同时考虑外集卡随机到达堆场执行装卸任务对于堆场中内集卡调度作业的影响。采用粒子群算法[11]（Particle Swarm Optimization，PSO）求解建立优化模型。粒子群算法的优势在于简单容易实现，目前已广泛应用于函数优化。考虑不确定因素的堆场集成调度优化更符合实际作业，对提高码头服务水平有着非常重要的意义，并为码头管理者解决实际作业调度提供重要的价值。

2 问题描述及假设条件

2.1 问题描述

港口内具体布局如图1所示：闸口是连接港内外的通道，闸口与岸边之间为港内作业，其中不同的港口设置堆场、泊位的数量以及方位有所不同[12]。卸船时桥吊首先将集装箱从船上卸至岸边集卡，再由集卡将箱子运送至指定堆场箱区内，此时场桥再将箱子从集卡放到指定箱位中。装船作业则是反向流程。问题优化的目标是在考虑外集卡随机到达情况下，给出一个内集卡和场桥装卸作业时间相互协调的任务分配方案，在考虑不确定因素并保证所有作业都已完成的情况下，使得场桥装卸作业时间最短，减少场桥和内集卡相互等待的时间，整体提升作业效率。场桥作业任务会因为外集卡的随机到达而增加，从而需要对场桥和内集卡进行重新调配。

图1 港口布局图

本文引入堆场作业的三大不确定因素：内集卡行驶速度、场桥作业时间及行走速度建立模型，按照上海港码头实际作业统计规律，用正态分布来处理这些随机变量。同时外集卡到达时间服从Poisson分布。

2.2 假设条件

假设所调用的集卡全部为单挂集卡，集卡运输的集装箱全部为40英尺标准箱，相同设备作业能力没有差别，将所有装卸作业任务编号并按照一定规则排序。有关模型的其他假设如下：

假设1装卸任务固定,共有M个场桥参与堆场装卸作业。所有装船箱任务共n1个,卸船箱任务n2个。

假设2所有任务对应的集装箱堆场位置和岸桥位置已知，在内集卡任务分配完成后，选取最优路径完成装卸任务，不考虑交通问题，即每辆集卡完成各项装卸任务的行驶距离是已知的。内集卡作业的不确定性主要体现在行驶速度以及在场桥等待时间的不确定性上。

假设3所有任务分配给N辆内集卡,集卡l的重车和空车行驶速度为随机变量ηl和ξl；所有场桥的作业时间是随机变量，记为γ；场桥行走速度为随机变量，记为υ。

假设4每个场桥的工作时间从它开始第一项任务算起，并在该场桥完成分配到的最后一项任务时结束，总时间为第一个场桥开始任务到最后一个场桥完成任务之间的时间。

假设5外集卡在随机的时间到达指定堆场区域，该堆场区域的场桥在完成当期任务后对外集卡进行服务。

3 不确定环境下堆场设备集成调度优化建模

3.1 符号说明

将堆场内的作业抽象为一个不确定优化模型，需要将问题抽象为一个网络图。假设目前需要分配给内集卡和场桥的任务指令有n个，每个指令对应堆场和岸桥之间的装卸任务，并将装船任务组成的集合记为CH，卸船任务组成的集合记为UL，在网络图中对应于n个节点V={1,2,…,n}。引入虚拟任务点的概念[13]，一个虚拟任务点表示一项指令，任意两个虚拟节点i,j之间的距离为从虚拟任务点i的卸载点到 j的装载点之间的距离，记为dij。可见，集卡在任意两个虚拟任务点之间为空车行驶，且一般来说，dij≠dji。

为了将内集卡装载任务构造成一个回路，假设有一个虚拟任务点O，它到任意点之间的距离为0，即所有内集卡从虚拟任务点O开始任务。假设任务分配给N辆内集卡，用1≤l≤N 记为表示车辆序列；假设任务分配给M个场桥，同样表示场桥序列。

决策变量如下：

Xl

ij表示内集卡l是否从第i项任务的卸载点直接至第 j项任务的装载点。即当Xlij=1时，内集卡完成任务i之后去完成任务 j。记内集卡l完成的任务集合为Jl，显然有

Ym表示场桥m是否在完成第i个装卸任务后完成

ij第 j个装卸任务。即当Yimj=1时，场桥m完成任务i后去完成任务 j。记场桥m完成的任务集合为Qm，显然有

模型中的其他参数如下：

ηl和ξl为内集卡l的重车行驶速度和空车行驶速度，这两组是不确定变量。

γ为场桥完成一吊普通箱装卸作业的时间，是不确定变量。

υ为场桥在堆场指定区域内的移动速度，是不确定变量。

Sm,Fm为场桥m开始和结束工作的时刻。

ak为完成全部作业的时间内第k辆外集卡(k=1,2,…,K)到达堆场指定区域的时刻。

δ为场桥对外集卡进行服务的平均时间。

3.2 数学模型

3.2.1 复杂模型

为了体现场桥服务外集卡对整体码头作业效率的影响，考虑增加一个关于外集卡的“奖励项”。假设作业期间场桥服务外集卡帮助外集卡节省的等待的时间为，奖励项函数定义为，其中 f(⋅)为单调递增函数，满足 f(0)=0。构建数学模型M1如下：

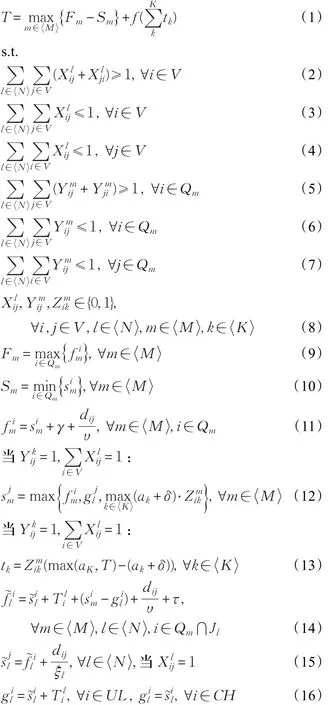
式（1）为目标函数，表示场桥完成全部任务的总时间，目标是使其最小。Xlij,Ymij为决策变量；约束条件（2）保证所有任务都已完成，即内集卡对于每个虚拟任务点至少执行了一次；约束条件（3）与（4）保证每项任务只由一辆内集卡一次完成，并没有重复执行相同的任务；式（5）至式（7）保证场桥执行了所有任务有且仅有一次；式（8）表示自变量的取值范围为0-1离散变量；式（9）与式（10）表示场桥开始和结束工作的时刻和场桥每项任务开始和结束工作的时刻之间的关系；式（11）表示场桥每项任务开始和结束时刻之间的关系；式（12）表示场桥完成一项任务后，下一项任务开始的时刻，这里考虑了场桥是否被调配为外集卡服务；式（13）表示场桥为外集卡服务后，外集卡减少的等待时间；式（14）表示内集卡完成一项装卸任务所需时间，包括内集卡运行时间和岸桥平均等待时间（Til）+堆场场桥等待时间场桥移动到下一装卸任务位置的时间场桥作业时间（τ），由此得到内集卡完成一项任务起始时刻之间的关系；式（15）中表示内集卡在两个虚拟任务点之间空车行驶的时间，由此可得集卡在前一项任务完成时刻和后一项任务开始时刻之间的关系；式（16）表示装船和卸船时，内集卡l被分配去完成任务i到达堆场指定位置的时刻gil和内集卡l开始任务i的时刻il之间的关系。

模型M1与文献[14]相比，部分约束条件类似，但模型M1更为复杂，表现在以下几个方面：

（1）文献[14]只考虑了内场集卡和场桥的优化，而模型M1兼顾了外集卡作业服务问题。

（2）模型M1的目标函数引入了关于外集卡节约等待时间奖励项，奖励函数的确定会对模型求出的最优解有很大的影响。

（3）外集卡节约的等待时间和模型优化目标函数中的作业总时间是耦合的，因此也增加了模型的复杂度和求解难度。

考虑到实际作业的特点，作业优化主要以内集卡装卸作业为目标，在保证内集卡作业效率的前提下才会考虑外集卡服务的问题。注意到关于模型M1的目标函数如何选取和以及模型如何快速准确求解都比较困难，在下一小节中，将简化上述模型，针对外集卡服务给出一个贪婪类算法。

3.2.2 简化模型

针对引入外集卡服务后模型M1求解复杂的问题，本小节给出一种更为实用的贪婪算法：当场桥完成上一项装卸任务，执行下一个任务的集卡还没有到达场桥，安排场桥外等待区域内排队时间最长的外集卡服务。于是得到如下简化模型M2：

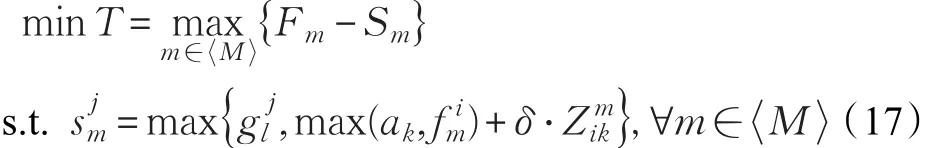
约束条件为模型M1中的式（1）～（11）、（13）～（15）以及式（17）。式（17）表示场桥完成一项任务后，是否被调配为等待时间最长的外集卡服务。

3.3 模型性质描述

根据集装箱码头作业特点，通常场桥一般只会服务一个指定的区域，不会像集卡一样在整个堆场范围移动，所以场桥对于装卸任务的选择是有限制的。在目前绝大多数实际作业中，场桥完成装卸任务的顺序一般由它服务区域内等待的内集卡执行的装卸任务决定，即在场桥服务区域内，正在等待的集卡需要执行哪一项装卸任务，场桥就执行对应的装卸任务。当有多辆集卡同时在场桥服务区域内等待时，为了减少场桥的运行时间，通常会优先服务距离当前装卸作业位置距离的集卡。根据上述模型描述，本文求解模型时充分考虑决策变量之间的联系，给出通过和其他参数来确定的方法。按照排队论的基本原则，将场桥看作服务台，到达堆场的集卡根据装卸任务到达指定位置。当场桥完成某项装卸任务后，下一项任务就是在堆场指定区域等待距离最近的集卡所执行的装卸任务。多次实际模拟计算以及对码头作业的调研证明，本文模型更加符合真实作业环境，并可以得到有效的优化结果。

4 粒子群算法求解过程

PSO是一种新的模仿鸟类群体行为的智能优化算法，现已成为进化算法的一个新的重要分支。和遗传算法相似，它也是从随机解出发，通过迭代寻找最优解，也是通过适应度来评价解的品质。但是它比遗传算法规则更为简单，它没有遗传算法的“交叉”（Crossover）和“变异”（Mutation）操作。它通过追随当前搜索到的最优值来寻找全局最优。本文建立的模型中，所有自变量为离散变量，即设备作业的任务选择。当这些离散变量确定以后，根据实际码头作业的数据，可以确定设备的位移、速度以及完成时间等连续变量。本文采用的PSO算法快速计算这些离散变量，通过适应度函数的变化趋势来得到近似最优值。

4.1 算法流程

PSO初始化为一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，称为个体极值 fk；另一个极值就是整个种群目前找到的最优解，这个极值是全局极值 fbest。

在一个n维的目标搜索空间中，n为装卸任务总数。整个粒子群体由K个粒子构成，每个粒子看作n维空间中的一个点。 x=(xk1,xk2,…,xkn)，xki∈[1,N]，且xki为整数，表示任务分配给内集卡的编号。在粒子位置给定后，每辆集卡分配到任务编号。对于每一辆集卡来说，以第一个编号作为开始任务，完成每项后，采用贪婪法则选择距离最近的任务为下一任务。同时，考虑到协调场桥的需要，让一半集卡的第一项任务为装船任务，另一半集卡的第一项任务为卸船任务。每个粒子对应的速度为v=(vk1,vk2,…,vkn)。初始状态通过随机值给出。

构造不确定情况下堆场调度优化的粒子群算法如下（图2）：

步骤1算法初始化，随机给出初始状态粒子群位置并计算适应度函数。

步骤2算法开始，更新粒子位置和速度。

每一步迭代过程中，粒子根据单个粒子和所有粒子的飞行经验进行动态调整。 fk=(fk1,fk2,…,fkn)，k=1,2,…,K为第k个粒子迭代到目前为止搜索到的最优值。 fbest=(fb1,fb2,…,fbn)为整个粒子群粒子迭代到目前为止搜索到的最优值。这两个因素决定下一步搜索的速度和位置。粒子根据以下式子进行更新和调整自己的位置：

参数w是惯性权重，表示保持原来速度的系数，采用线性约减策略来决定w的值，即

c1和c2是粒子跟踪自己历史最优值和群体最优值的权重系数，也称学习因子或加速因子，使粒子能够调整自身方向，向粒子本身最优值和群体最优值靠近，通常设置为2；rand1和rand2表示[0,1]区间内均匀分布的随机数，这两个参数是用来保持整个粒子群个体的多样性；ρ表示更新位置的步长，通常称为约束因子，设置为1。

据有关数据统计，住院期间的母乳喂养率较高，出院后则大幅下降。出生后6个月内的纯母乳喂养率仅为20.8%。产褥期会出现多种母乳喂养的问题，导致产妇对母乳喂养信心不足，甚至停止母乳喂养。

步骤3解码。

由于问题的特殊性，这一模型的每个粒子的位置代表任务分配给内集卡的编号，必须是1～N之间的整数。因此在粒子群算法每次迭代更新位置之后，都需要进行解码，解码方式为对于粒子位置每个分量取整，这样就可以得到有实际意义的粒子位置。由于在算法过程中粒子进行运动和解码时，并未涉及堆场作业和各种不确定因素，因此粒子群算法中的这几个主要步骤就比较容易实现，从而提升了算法的效率。

步骤4计算适应度函数。

每步迭代之后，根据每个粒子新的位置，可以计算每个粒子的适应度函数。计算时，本文模型基于排队论的基本原理计算场桥在堆场装卸作业以及集卡行驶和等待的时间，具体计算流程如图2所示。在给定某个粒子的位置后，可以得到集卡作业调度方案，此时运用蒙特卡洛方法实现集卡在堆场等待和装卸作业过程，计算从第一个场桥开始工作至场桥结束所有装卸任务的总时间。同时，在计算过程中，由于集卡行驶速度和场桥装卸和移动时间为不确定变量，故采用模拟的方法估计函数值。

图2 适应度函数计算流程图

步骤5判断终止条件,决定迭代是否继续进行下去。

综上所述，粒子群算法流程如图3所示。

图3 粒子群算法流程图

4.2 分布处理

与以往确定性模型的文章一般采用统计数据的均值代替随机变量不同，本文根据上海港码头实际作业数据统计规律，内集卡在完成运输任务的行驶时间基本服从正态分布N(μ,σ)，其均值 μ 通过统计抽样，由距离除以平均速度估计得到；轻车和重车在运输时的平均速度相差不大，但重车行驶受到外界影响较多，因此标准差σ相对较大。场桥在堆场指定区域的行走速度以及作业时间基本服从正态分布。同时外集卡到达时间服从Poisson分布。

5 算例与分析

5.1 试验算例

5.2 评价与分析

选取种群大小K=10，应用Matlab软件求解。上百次的试验结果显示，选取参数wmax=1,wmin=0.5时，算法的计算结果和速度都比较理想。本文观察了500步迭代的考虑不确定性因素的模型和一般确定性模型的目标函数值如图4所示。图中表明，考虑不确定性因素的模型中，由于粒子群算法适应度函数具有随机性，优化模型的目标函数的变化并不是完全单调下降的，但整体上具有下降的趋势。从目标函数值来看，作业时间从初始状态的50 min最后减少到接近31～33 min，大大提升了集卡运输作业效率。大约200多步迭代之后，目标函数值的变化幅度明显缩小，逐步接近最优值。同时，由于外集卡到达时间具有随机性，在完成指定任务作业过程中，外集卡到达的数量会有一些差异，这也就导致迭代过程始终具有较大的震荡性，目标函数值会在一定范围的数值中变化。与此同时从图中可知，粒子群算法的收敛性态并没有因为随机项的引入带来很大的影响，所以它在求解不确定情况下兼顾外集卡作业的堆场设备作业优化问题上是非常有效的，而本模型显然更贴近实际作业状况。

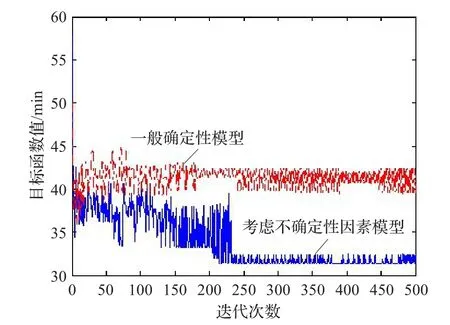
图4 考虑不确定性因素模型和一般确定性模型的目标函数结果比较

同时，图4也是对采用粒子群算法得出的一般确定性模型结果与考虑不确定性因素模型的结果进行比较。一般确定性模型是将不确定模型中的随机变量用它们的期望值代替，外集卡的到达时刻是随机值。算法的其他所有步骤都和不确定模型算法相同。图4可得，考虑不确定因素模型收敛结果最优值为31.5 min，一般确定性模型为42.2 min。一般确定模型算法结果收敛性态很差，得到的最优值估计要差很多。

图5是在不考虑外集卡随机到达影响下，一般确定性模型与考虑不确定性因素模型的堆场设备作业时间的比较。考虑不确定因素模型最终计算结果约为28.5 min。所以对比图4和图5的结果可知，考虑外集卡作业后，堆场整体作业时间大约增加了3 min，而在30 min左右的作业时间内，到达外集卡数量的平均值为3辆。堆场对于外集卡总的作业时间约为100 s×3=300 s。所以，综合考虑外集卡作业可以有效提升堆场对于内外集卡作业的整体效率。

图5 不考虑外集卡到达影响的一般确定性模型与不确定性模型结果比较

本文给出的算法在计算复杂度方面有很大的优势。如果采用遍历算法，其复杂度随着自变量数量增加指数上升；而从上面的算例中发现，本文给出的PSO算法在200多步迭代后就计算得到了比较好的近似最优值，计算复杂度是可控的。

6 结论

本文建立集装箱码头堆场设备集成调度优化模型，模型中同时考虑了内集卡、场桥和外集卡之间的相互协调，并且考虑了实际作业中的不确定性因素，包括：内集卡行驶速度、场桥作业时间和行走速度，以及外集卡的到达时间。与传统只考虑确定环境下内集卡和场桥的调度优化相比，本文模型可以提高堆场作业调度的整体性与协调性，并更贴近实际作业情况，提高码头服务质量。粒子群算法可以提高模型的求解效率，算例分析结果表明，该模型和算法可以在兼顾外集卡作业的情况下有效解决不确定环境下集装箱码头堆场的集成调度优化问题。所设计的算例规模虽小，但已经能够说明模型的合理性。

本文今后的研究重点和方向包括考虑外集卡在闸口服务时间对于堆场设备作业的影响，同时协调内外集卡的作业从而进一步提升作业效率等。

[1]杨朋，缪立新，戚铭尧.多载具自动化存取系统货位分配和拣选路径集成优化[J].清华大学学报：自然科学版，2011，51（2）：261-266.

[2]赵宁，宓为建，何军良.集装箱码头发箱任务的集卡指派模型[J].上海海事大学学报，2011，32（1）：8-12.

[3]Kim K H，Park Y M.A crane scheduling method for port container terminals[J].European Journal of Operational Research，2004，156（3）：752-768.

[4]Ng W C，Mak K L.Yard crane scheduling in port container terminals[J].Journal of Applied Mathematics，2005，29（3）：263-276.

[5]Ng W C，Mak K L，Zhang Y X.Scheduling trucks in containerterminalsusing a genetic algorithm[J].Engineering Optimization，2007，39（1）：33-47.

[6]韩晓龙，丁以中.集装箱码头港口龙门吊配置优化研究[J].中国航海，2008，31（1）：6-9.

[7]Cao J X，Lee D H，Chen J H，et al.The integrated yard truckand yard cranescheduling problem：Benders’decomposition-based methods[J].Transportation Research，2010（4）：344-353.

[8]乐美龙，包节，范志强.龙门吊与集卡协同调度问题研究[J].计算机工程与应用，2012，48（14）：241-248.

[9]刘艳，周鹏飞，康海贵.集装箱堆场箱位分配模糊优化研究[J].水运工程，2009（11）：1-5.

[10]周鹏飞，李丕安.不确定条件下集装箱堆场出口箱具体箱位优选[J].工业工程，2013，16（1）：25-30.

[11]Tandon V，Mounayri H E，Kishawy H.NC end milling optimization using evolutionary computation[J].International Journal of Machine Tools and Manufacture，2002，42（5）：595-605.

[12]李莉.集卡港内作业与港外运输综合调度研究[D].天津：天津工业大学，2011.

[13]李臻，雷定猷.多车场车辆优化调度模型及算法[J].交通运输工程学报，2004，4（l）：83-86.

[14]Lu Yiqin，Le Meilong.The integrated optimization of container terminal scheduling with uncertain factors[J].Computers and Industrial Engineering，2014，75：209-216.

LU Yiqin

School of Economicsamp;Management,Shanghai University of Electric Power,Shanghai 200090,China

Integrated scheduling optimization of yard equipment with uncertain factors at container terminal.Computer Engineering and Applications,2017,53（21）：247-253.

On the scheduling optimization of the yard equipment,more studied the combined dispatching of the inner container trucks and yard cranes under deterministic conditions,and less considered the random arrival time of the outer container trucks.The uncertain factors including the speed of the inner container trucks,the speed and the operation time of the yard cranes are considered.And according to the effect of the random arrival time of the outer container trucks on the scheduling operation of the inner container trucks,the optimization model considering the uncertain factors of the integrated scheduling of the yard equipment is established.The objective is to minimize the operation time of the yard equipment considering the random arrival time of the outer container trucks.So the particle swarm optimization algorithm is designed to settle the model,and the optimized results of the uncertain model are compared with that of the deterministic model.The numerical experiments and results represent that the model and the algorithm truly and effectively reflect the effect of the uncertain conditions on the operation of the yard equipment.

uncertain factors;integrated scheduling;yard equipment;outer container trucks

A

U691

10.3778/j.issn.1002-8331.1704-0437

中小物流企业信息化方案与决策（No.H2016-029）；国家自然科学基金（No.71171129）；上海市科委科研计划项目（No.12510501600，No.14DZ2280200）。

卢毅勤（1980—），女，博士，讲师，研究领域为集装箱码头作业系统调度优化，E-mail：lu_yiqin@163.com。

2017-05-03

2017-06-20

1002-8331（2017）21-0247-07