分类解析导数知识中的易错点

■江苏省高港中等专业学校 杨美琴

分类解析导数知识中的易错点

■江苏省高港中等专业学校 杨美琴

导数是研究函数性质的有力工具,特别是在求曲线的切线方程、研究函数的单调性与极(最)值等问题中,凸显导数卓越的解题功效,因此,与导数有关的高考试题备受青睐。由于同学们对导数的有关概念理解不透彻,辨析不清楚,致使解题过程中易出现一些错解。本文对导数知识的易错点归类剖析,给出警示,希望能助同学们一臂之力。

易错点1——忽略导数定义中的整体增量

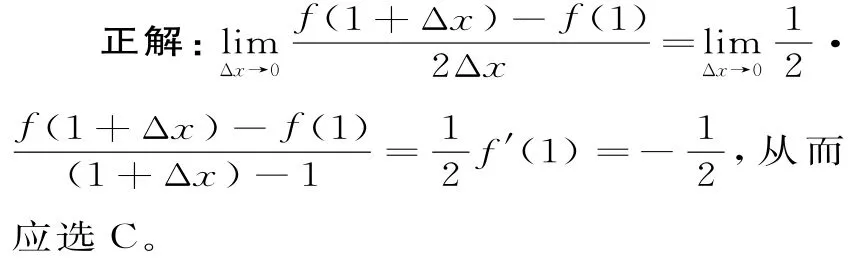
易错点2——混淆过曲线某点的切线与在某点处的切线

例2 求过点A2,8( ),且与曲线f x()=x3相切的直线方程。

错解:f'x()=3x2,所以f'2()=1 2,则切线方程为y-8=1 2x-2( ),所以y=1 2x-1 6。

剖析:错解混淆了“过某点”与“在某点”处的切线的概念,因此应考虑A2,8( )为切点和不是切点两种情况。

(1)当A2,8( )为切点时,由错解可得到切线方程为y=1 2x-1 6。

综上所述,所求切线方程为y=1 2x-1 6或y=3x+2。

警示:(1)曲线的切线不一定和曲线只有一个交点。(2)“在”某一点的切线和“过”某一点的切线是两个不同的概念。(3)在某一点的切线若有则只有一条,而过某一点的切线往往不只是一条。(4)用导数求切线的斜率时,必须要设出切点,采取“待定切点法”求解。如本题当A不是切点时,设切点为切线斜率为k,三个未知量需用三个条件求解:①y0=f (x0),②k=f'(x0),解得切点坐标,得到其切线方程。

易错点3——混淆“导函数值正负”与“原函数图像升降”的关系

例3 已知函数f(x)的导函数f'(x)的图像如图1所示,则y=f(x)的图像最有可能是图2中的____。

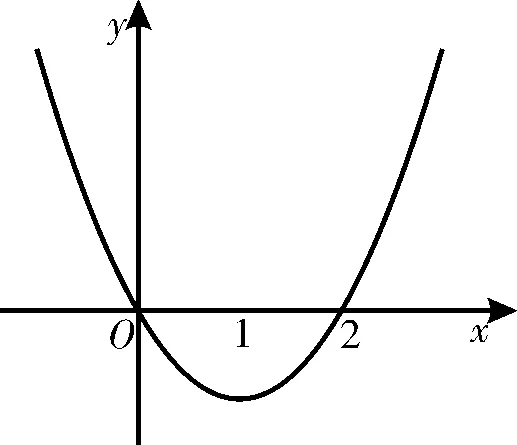
图1

错解:选A,B,D。

剖析:概念不清,凭空乱猜结论。由于f'(0)=f'(2)=0,且两边值符号相反,故0和2为极值点;又当x＜0和x＞2时,f'(x)＞0,当0＜x＜2时,f'(x)＜0,所以函数f(x)在(-∞,0)和(2,+∞)上为增函数,在(0,2)上为减函数。正确答案:C。

警示:函数与导函数的对应是:①导函数的零点与原函数的极值点关系——极值点的导数值为0;②导函数值的符号与原函数单调性的关系——原函数看增减,导函数看正负。

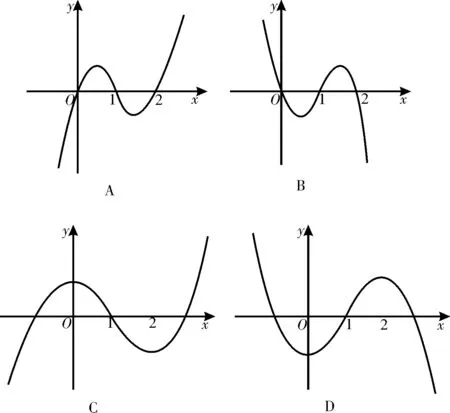
图2

跟踪演练3 (山西省运城市2 0 1 7届高三上学期期中)已知函数f(x)=x2+c o sx,f'(x)是函数f(x)的导函数,则f'(x)的图像大致是图3中的( )。

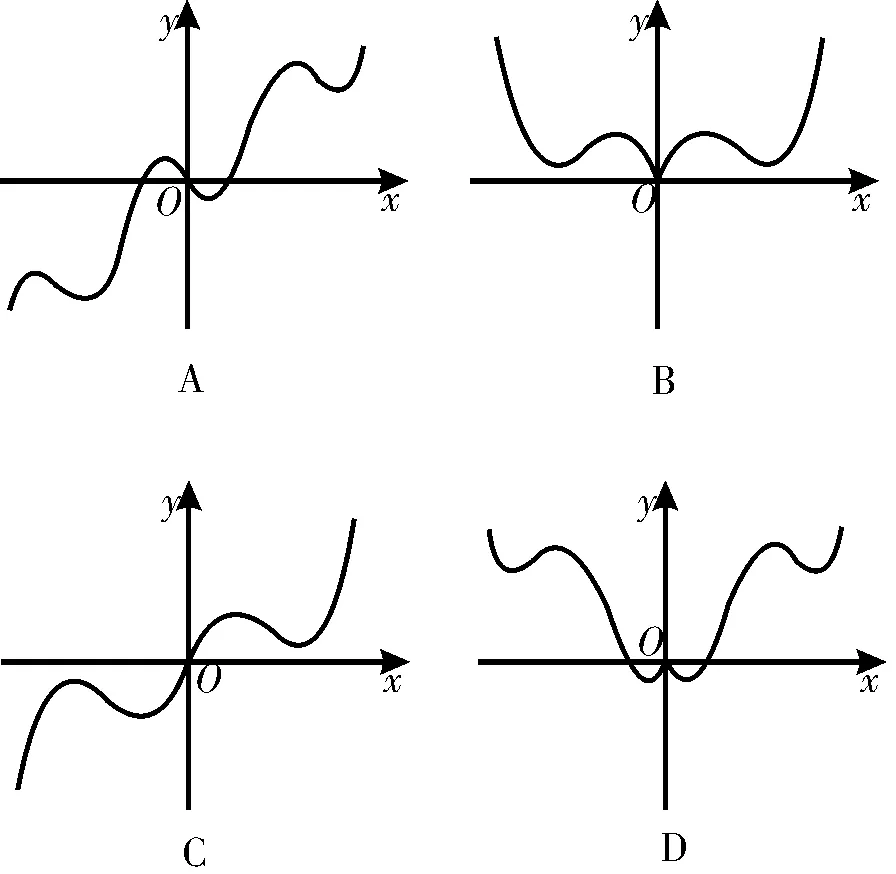
图3

易错点4——忽视“有极值”的条件和极值的意义

例4 已知f(x)=x3+a x2+(a+6)x+1在R上有极值,求实数a的取值范围。

错解:由题意知,f'(x)=3x2+2a x+(a+6)=0在R上有实数解,所以Δ≥0,即4a2-1 2(a+6)≥0⇒a≤-3或a≥6。

剖析:错解中将有极值的必要条件f'(x)=0当作充要条件使用了。由题意知,f'(x)=3x2+2a x+(a+6)=0在R上有实数解,所以Δ≥0,即4a2-1 2(a+6)≥0⇒a≤-3或a≥6。显然,当a=-3时,f'(x)=3x2+2a x+(a+6)=3(x-1)2≥0,1不是极值点,f(x)在R上没有极值;当a=6时,f'(x)=3(x+2)2≥0,-2不是极值点。综上,所求a的取值范围为(-∞,-3)∪(6,+∞)。

警示:对于可导函数f(x),f'(x0)=0是在x0处取得极值的必要而非充分条件,解题时还要验证在x0附近f'(x0)是否异号。一元三次函数有极值的充要条件是其导函数的判别式大于零。

跟踪演练4 (2 0 1 7年第三次全国大联考新课标卷Ⅰ)已知函数f x()=a x-x2-l nx存在极值,若这些极值的和大于5+l n2,则实数a的取值范围为( )。

A.(-∞,4) B.(4,+∞)

C.(-∞,2) D.(2,+∞)

易错点5——混淆f(x)在D上是增函数(减函数)与f'(x)≥0(f'(x)≤0)在D上恒成立

例5 已知函数f(x)=-x3+a x+2(a∈R)在区间[-1,1]上是增函数,求a的取值范围。

错解:由函数f(x)=-x3+a x+2在区间[-1,1]上是增函数,得f'x()=-3x2+a≥0的解集是[-1,1],则x=±1是方程-3x2+a=0的根,故a=3。

剖析:“函数f(x)=-x3+a x+2(a∈R)在区间[-1,1]上是增函数”与“函数f(x)=-x3+a x+2(a∈R)的增区间是[-1,1]”是有区别的,前者的区间为后者区间的子集。

由函数f(x)=-x3+a x+2在区间[-1,1]上是增函数,得f'x()=-3x2+a≥0在[-1,1]上恒成立,即a≥3x2在[-1,1]上恒成立,故a≥3。

警示:函数f(x)的增(减)区间是区间D,实质是指f(x)仅有一个增(减)区间D;函数f(x)在区间D上是增(减)函数,实质是指区间D是f(x)的增(减)区间的一个子区间。可导函数y=f(x)在(a,b)上是增(减)函数的充要条件是:对任意的x∈(a,b),都有f'(x)≥0或f'(x)≤0,且f'(x)在(a,b)的任何子区间内都不恒等于零。特别要注意:已知函数的单调性,求参数取值范围时,一定要考虑“等号”是否可以取到。

易错点6——利用导数研究单调性忽视分类讨论

例6 求函数f (x)=x+2(x∈x(0 ,t] ,t为大于0的常数)的单调区间和最值。

剖析:t为大于零的常数,f'(x)=0的两个零点是否在所给的区间0,t( ]内,取决于t的取值,本题误认为t＞ 2,忽视了对常数t的分类讨论。

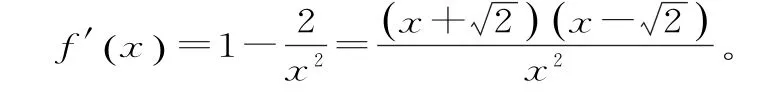
(1)当t＞2时,就是上述答案;

(2)当t=2时,函数f(x)的单调减区间是0,2( ],f2()=2 2是最小值,无最大值;

警示:利用导数法求解单调区间,只需求导判断零点,用区间上导函数的正负关系就可得到函数的增减性,也就得到单调区间,进而找到函数的极值点,从而求得最值。要注意导函数值的零点和所给区间的位置关系,常常要分类讨论求解。

跟踪演练6 (四川省宜宾市2 0 1 7届高三第二次诊断检测)函数f(x)=a x3+3x2+3x(a≠0)。

(1)讨论f(x)的单调性;

(2)若f(x)在区间(1,2)上是增函数,求a的取值范围。

正解:(1)f'(x)=3a x2+6x+3,=0的判别式Δ=3 6(1-a)。

①若a≥1,则f'(x)≥0,故此时f(x)在R上是增函数。

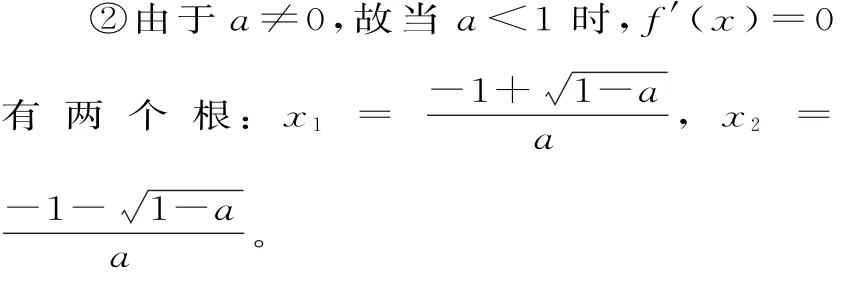
若0＜a＜1,则当x∈(-∞,x2)或x∈(x1,+∞)时,f'(x)＞0,故f(x)分别在(-∞,x2),(x1,+∞)上是增函数;当x∈(x2,x1)时,f'(x)＜0,故f(x)在(x2,x1)上是减函数。

若a＜0,则当x∈(-∞,x1)或(x2,+∞)时,f'(x)＜0,故f(x)分别在(-∞,x1),(x2,+∞)上是减函数;当x∈(x1,x2)时,f'(x)＞0,故f(x)在(x1,x2)上是增函数。

(2)当a＞0,x＞0时,f'(x)=3a x2+6x+3＞0,故当a＞0时,f(x)在区间(1,2)上是增函数。

当a＜0时,f(x)在区间(1,2)上是增函数,当且仅当f'(1)≥0且f'(2)≥0,解得-≤a＜0。

易错点7——混淆极值与最值的概念致错

例7 求函数f(x)=x3-2x2+x在-3,3[ ]上的最值。

错解:f'(x)=3x2-4x+1=(3x-1)·(x-1),所以极值点为x=1或x=

剖析:需注意在闭区间上的最值应是区间内的极值点的值与闭区间端点的值进行比较而得,而不能简单地把极值等同于最值。f'(x)=3x2-4x+1=(3x-1)(x-1),所以极值点为x=1或x=-

警示:函数的极值和最值是不同的概念,在一个区间上可能有几个极大值和极小值,极大值与极小值之间无确定的大小关系,即一个函数的极大值未必大于极小值,因此,求函数在闭区间上的最值需要将函数的一切极值和其端点值进行比较才能确定。由于高考只对单峰函数有要求,故在求解闭区间上的函数的最值时,只需求解极值点和其端点值即可获解。

跟踪演练7 (2 0 1 7年内蒙古包头十校联考)设函数f (x)=x3-3x+1,x∈[- 2,2]的最大值为M,最小值为m,则M+m=____。

正解:由已知条件可知f'(x)=3x2-3=3(x +1)(x -1),令f'(x)=0,解得x=-1或x=1,当x∈ [- 2,-1]时,f'(x)＞0,函数单调递增,当x∈ (- 1,1)时,f'(x)＜0,函数单调递减,当x∈ (1 ,2]时,f'(x)＞0,函数单调递增,经过计算f(- 2)=-8+6+1=-1,f(-1)=-1+3+1=3,f(1)=1-3+1=-1,f(2)=8-6+1=3,所以函数的最大值是3,最小值是-1,则M+m=2。

易错点8——认为分段函数极值只能在导数为零的点处取得

剖析:在确定极值时,只讨论满足f'x()=0的点x0附近导数的符号变化情况是不全面的,在导数不存在的点处也可能存在极值。在上述解法中,补充在x=-2和x=3处函数取得极小值0。

警示:分段函数的极值可能存在于导数为零处,也可能存在于函数的分段点处。作出其图像,数形结合是最保险的方法。

易错点9——用导数研究数列性质时忽略定义域

例9 已知数列{an}的通项为an=n·an(a＞0),且an＞an+1对所有正整数n均成立,求实数a的取值范围。

错解:令f(x)=x·ax(a＞0),由an＞an+1可得函数f(x)在区间[1,+∞)上单调递减,故f'(x)=ax(1+x·l na)≤0在区间[1,+∞)上恒成立。

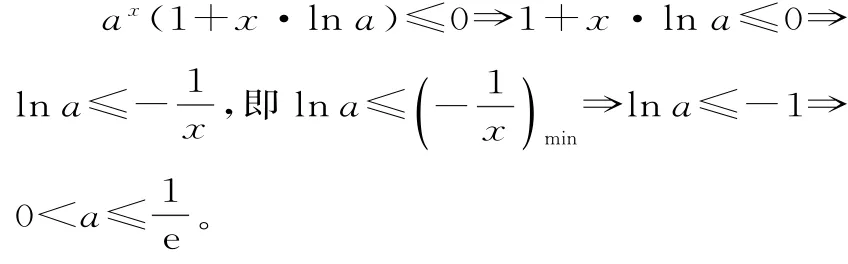
剖析:错解错在将f(n)＞f(n+1)看作是函数f(x)在区间[1,+∞)上单调递减,事实上,(n,an)只是该函数的图像上一系列的点,因此要使a1＞a2不一定有函数f(x)在区间[1,2]上单调递减。

警示:用函数的单调性解决数列单调性问题时,不能直接求导,也不能将数列的单调性等同于函数的单调性,借助函数的单调性时需要增加比较第一、二两项的大小。

(责任编辑 王福华)