集合、函数、导数核心考点A卷答案

集合、函数、导数核心考点A卷答案

一、选择题

1.C 2.C 3.D 4.A 5.D 6.C 7.D 8.A 9.B 1 0.A 1 1.D 1 2.D 1 3.C 1 4.A 1 5.C 1 6.B 1 7.B 1 8.D 1 9.C 2 0.D 2 1.A 2 2.B 2 3.C 2 4.B 2 5.C 2 6.A 2 7.A 2 8.B 2 9.B 3 0.C 3 1.D 3 2.B 3 3.D

二、填空题

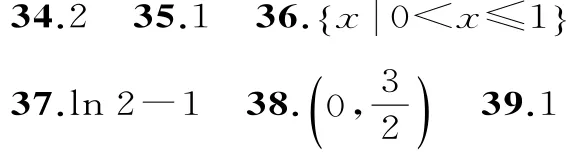
4 0.2 4 1.3 4 2.(3,+∞) 4 3.①③④

三、解答题

4 4.(1)设f(x)=a x2+b x+c(a≠0),由f(0)=2,得c=2,所以f(x)=a x2+b x+2。因为f(x+1)-f(x)=2x+3,所以2a x+a+b=2x+3,所以所

以f(x)=x2+2x+2。

(2)由题意x2+2x+2＞-2x+m在[-1,1]上恒成立,即x2+4x+2＞m在[-1,1]上恒成立。令g(x)=x2+4x+2=(x+2)2-2,其对称轴为x=-2,所以g(x)在区间[-1,1]上是增函数,所以g(x)min=g(-1)=1-4+2=-1,所以m＜-1。

4 5.(1)设l o g2x=t,则x=2t,所以f(t)=a(2t)2-2·2t+1-a,所以f(x)=a(2x)2-2·2x+1-a。

(2)设2t=m(m＞0),则g(m)=a m2-2m+1-a(m＞0)。

当a=0时,g(m)=-2m+1,所以g(m)的值域为(-∞,1);

当x＜-4时,g'(x)＜0,故g(x)为减函数;

当-4＜x＜-1时,g'(x)＞0,故g(x)为增函数;

当-1＜x＜0时,g'(x)＜0,故g(x)为减函数;

当x＞0时,g'(x)＞0,故g(x)为减函数。

综上,g(x)在(-∞,-4)和(-1,0)内为减函数,在(-4,-1)和(0,+∞)内为增函数。

4 7.(1)由题意令x=y=0,所以f(0)=0。令y=-x,代入f(x+y)=f(x)+f(y),得f(0)=f(-x)+f(x)=0,所以f(-x)=-f(x)。所以函数f(x)为奇函数。

g'x()和g x()在x∈0,+∞()上的变化情况如表1。

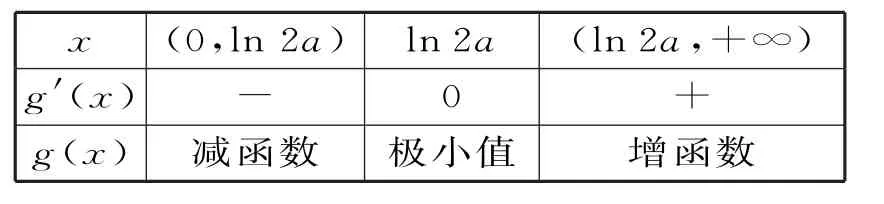
表1

当x∈(0 ,l n2a)时,g (x)＜g(0)=1-2a＜0,即 f'(x)＜0。所 以 f (x)在(0 ,l n2a)上为减函数,所以f (x)＜f(0)=0,与条件矛盾,故舍去。

4 9.(1)函数f(x)的定义域是(0,+∞),由已知可得f'(x)=2x-(a-2)-=

当a≤0时,f'(x)＞0对任意x∈(0,+∞)恒成立,所以函数f(x)在区间(0,+∞)上单调递增;当a＞0时,由f'(x)＞0得x＞,由

(2)当a=1时,f(x)=x2+x-l nx,要证明f(x)+ex＞x2+x+2,只需证明exl nx-2＞0。设g(x)=ex-l nx-2,则问题转化为证明对任意的x＞0,有g(x)＞0。

当x变化时,g'(x)和g(x)的变化情况如表2所示。

表2

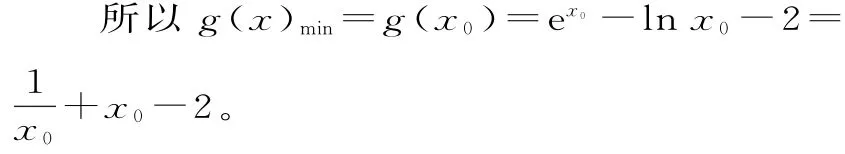
因为x0＞0,且x0≠1,所以g(x)min＞2 1-2=0,因此不等式得证。

(责任编辑 刘钟华)

编者的话:同学们在演练的过程中,如果需要更为详细的参考答案,请扫描右边的二维码,关注编辑部的官微“高中数学解题反思”,不但能获悉详细参考答案,还可以另辟蹊径,开拓知识视野,学会解题反思!