活用配方法巧解题
廖辉盛
(江西省赣州市安远县塘村学校,江西 赣州 342100)
活用配方法巧解题
廖辉盛
(江西省赣州市安远县塘村学校,江西 赣州 342100)
配方法是解一元二次方程的重要方法.用配方法解一元二次方程的一般步骤为:(1)移项;(2)二次项系数化为1;(3)配方,即把原方程化为(x+m)2=n(n≥0)的形式,再用直接开平方法.
配方法;因式分解;一元二次方程
配方法是一元二次方程解法中非常重要的一种方法,其实质是一种恒等变形,它通过加上并且减去相同的项,把算式的某些项配成完全n次方的形式,通常是指配成完全平方式, 配方法在中学数学中的应用非常广泛,本文通过例题谈谈它的一些应用.
一、应用配方法解方程
例1 解方程:2x2-3x+1=0.
分析用配方法解一元二次方程的一般步骤是:
1. 将二次项的系数化为1;
2.移项,使含未知数的项在左边,常数项在右边;
3.配方,方程两边都加上一次项系数一半的平方;
4.将方程化为(x+m)2=n的形式;
5.用直接开平方法进行求解(n<0无解).
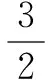
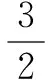
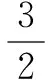



二、应用配方法分解因式
例2 分解因式x4+x2+1.
分析观察题目发现中间项系数如果为2时,即符合公式.由此可考虑使用配方法解决.
解原式=(x4+2x2+1)-x2=(x2+1)2-x2=(x2+x+1)(x2-x+1).
三、应用配方法求代数式的最值
例3 利用配方法求y=2x2-4x-7的最大值或最小值.
分析求最大值或最小值,必须将它们化成y=a(x+b)2+c的形式,然后再判断,当a>0时,它有最小值c;当a<0时,它有最大值c.
解y=2x2-4x-7=2(x2-2x+1)-7-2=2(x-1)2-9.
∵2(x-1)2≥0,∴2(x-1)2-9≥-9,故它的最小值是-9.
四、应用配方法化简求值
例4 已知x2y2+x2+4xy+13=6x,则x,y的值分别为____.
分析可将含x,y的方程化为两个非负数和为0的形式,从而求出两个未知数的值.
解∵x2y2+x2+4xy+13=6x,∴x2y2+4xy+4+x2-6x+9=0,
∴(xy+2)2+(x-3)2=0.
∵(xy+2)2≥0,(x-3)2≥0,
∴xy+2=0,x-3=0,∴xy=-2,x=3.


五、应用配方比较两个代数式的大小
例5 对于任意实数x,试比较两个代数式3x3-2x2-4x+1与3x3+4x+10的大小.
分析比较两个代数式的大小,可以作差比较,本题两个代数式相减后,可以得到一个二次三项式,将此二次三项式配方后,即可判断差的正负,从而可以判断两个代数式的大小.
解(3x2-2x2-4x+1)-(3x3+4x+10)
=-2x2-8x-9=-2(x+2)2-1<0,
所以对于任意实数x,恒有
3x3-2x2-4x+1<3x3+4x+10.
六、应用配方法证明等式、不等式
例6 已知方程(a2+b2)x2-2b(a+c)x+b2+c2=0中字母a,b,c都是实数.

分析一个方程含有四个未知数,看似无法求出a,b,c,x.但仔细观察发现,方程左边可以分成两组分别配方,正好得到两个完全平方式的和为0,利用非负数的性质可求出a,b,c,x之间的关系.
证明原方程拆成两个二次三项式为:(a2x2-2abx+b2)+(b2x2-2bcx+c2)=0,
∴(ax-b)2+(bx-c)2=0.
∵a,b,c,x都是实数,
∴(ax-b)2≥0,(bx-c)2≥0.
∴ax-b=0,bx-c=0.

[1]张晓林.配方法求二次函数顶点式中的典型错误[J].初中数学教与学,2011(07).
[责任编辑:李克柏]
G632
A
1008-0333(2017)29-0019-02
2017-07-01
廖辉盛(1985.12-),男,本科,中学一级教师,从事初中数学教学研究.

