旋转弹气动力建模与飞行轨迹仿真

王刚，邢宇，朱亚楠

旋转弹气动力建模与飞行轨迹仿真

王刚＊，邢宇，朱亚楠

西北工业大学 航空学院，西安 710072

运用一种自回归滑动平均（ARMA）的时域气动力建模方法，以计算流体力学与刚体动力学（CFD／RBD）耦合仿真的输出结果为样本，对旋转弹的非定常气动力进行建模。利用建立的气动力模型与刚体动力学方程求解模块耦合，实现了旋转弹轨迹的快速仿真，并讨论了不同的建模方式对仿真精度的影响。算例结果表明：采用气动力模型与刚体动力学方程耦合仿真技术可以在不同初始发射条件下进行旋转弹飞行姿态与运动轨迹预测，且与CFD／RBD仿真结果吻合较好，证明ARMA气动力建模方法可以在保证旋转弹轨迹预测精度的同时大幅缩短仿真时间，节省计算资源。

自回归滑动平均；气动力建模；刚体动力学；非定常气动力；轨迹仿真

旋转弹具有控制系统简单、抗干扰能力强和成本低的优势，是目前枪弹、反坦克导弹和便携式导弹的常用弹种［1］。在新型旋转弹的研发过程中，研究人员需要掌握设计对象的气动特性、稳定性和飞行轨迹等性能参数。考察上述旋转弹性能参数的常用手段有工程计算、风洞试验和自由飞行试验等。工程计算速度快，但由于过多的假设和简化，误差较大，难以满足精细化设计的要求；风洞试验和自由飞行试验［2］得到的数据可靠，但成本高、周期长且技术风险较大。

随着计算流体力学和飞行力学的发展，计算流体力学与刚体动力学（CFD／RBD）耦合计算方法逐渐成为飞行器运动姿态和轨迹预测的研究中常用的技术手段［3－6］。CFD／RBD 耦合方法可以精确计算和模拟飞行器的气动力与运动轨迹［5－7］。由于需要反复调用CFD分析工具求解流场获取非定常气动力，这种方法效率较低，对计算机硬件资源的要求较高。在工程实践中，人们往往需要在较短时间内获得多种初始条件下的仿真结果，这就使得CFD／RBD耦合方法在计算资源不够充裕的条件下显得力不从心。如果能够建立较快速而精确的非定常气动力模型，并利用它代替非定常CFD模块与刚体六自由度方程耦合进行仿真，就有可能实现快速、准确的飞行器轨迹仿真与姿态预测。

过去20多年中，气动力建模方法获得了广泛的关注，国内外研究人员提出了多种非定常气动力模型［8］。具有代表性的有代数多项式模型［9］、微分方程模型［10－13］、基于现代人工智能的模糊逻辑模型［14－15］和基于系统辨识技术的气动力建模技术［16－20］等。本文所采用的是已广泛应用于系统参数辨识问题中的自回归滑动平均（Autoregressive Moving Average，ARMA）时域气动力建模方法［19－20］。ARMA 方法的优点在于采用时域的CFD／RBD耦合仿真结果作为样本时，可直接确定模型系统的输入量和输出量，方便建模和应用。

本文选取美国陆军实验室（ARL）的超声速尾翼旋转弹试验模型作为研究对象［3－4］。该模型发射后的初始转速达到了2 518．39rad／s。在这种强烈的旋转角速度下，马格努斯效应显著［21－22］，这给 CFD／RBD 数值计算和非定常气动力建模都带来了挑战。首先运用CFD／RBD耦合方法对其自由飞行试验状态进行轨迹仿真，获得气动力建模的样本空间；进而采用ARMA时域气动力建模方法对CFD／RBD耦合仿真获取的运动系统进行参数辨识，建立该旋转弹的非定常气动力模型；然后利用建立好的气动力模型代替非定常CFD计算模块与刚体六自由度运动模块进行耦合，实现旋转弹飞行轨迹的快速仿真。为考察所建立的气动力模型的实用性，在改变旋转弹初始飞行条件的情形下，进行基于气动力模型的飞行轨迹仿真，并将计算结果与CFD／RBD耦合计算结果进行了对比。在此过程中，测试了不同的输入参数形式对建模结果的影响，分析了模型中部分参数的相互影响关系，提出了建模过程应注意的一些原则。

1 计算方法

1．1 CFD／RBD耦合方法

CFD计算模块采用的是作者所在团队自主编写的非结构混合网格雷诺平均Navier－Stokes方程求解程序HUNS3D［23］。这里简要介绍与本文工作相关的非定常流动CFD算法。

为了适应固体边界的六自由度运动，流动控制方程采用 ALE（Arbitrary Lagrangeian Eulerian）方法描述的非定常Navier－Stokes方程。ALE方法允许计算网格的刚体运动和任意变形，通过在流动控制方程中引入网格运动速度，将流体力学中的拉格朗日方法和欧拉方法进行统一描述。当网格运动速度为零时，ALE方法转化为欧拉描述；当网格运动速度为流体运动速度时，ALE方法转化拉格朗日描述。采用ALE方法描述的三维非定常雷诺平均Navier－Stokes方程的积分形式为

式中：Q＝［ρ ρu ρv ρw ρE］T，ρ为流体密度，E为总内能，u、v、w分别为旋转弹在体轴系下沿3个轴向的运动速度；Vgrid为网格运动速度；n为控制体单元边界外法向方向；F（Q）和G（Q）分别为无黏通量和黏性通量，其具体形式可参考文献［23］。在非定常流动计算中，式（1）中在F（Q）和G（Q）经过格心有限体积法空间离散后可采用全隐式双时间格式作时间推进求解。其基本思想是：在每一步真实物理时间步长中加入伪时间层上的“子迭代”来实现隐式系统方程的精确求解。同时，由于伪时间“子迭代”过程不受物理时间离散精度限制，因此可以采用定常流动求解当地时间步长、残值光顺等加速收敛技术来提高计算效率。

旋转弹在飞行过程中可以视作六自由度运动的刚体，惯性系下质心的平动方程：

体轴系下绕质心的转动方程为

刚体质心的运动学方程为

刚体姿态角的运动学方程为

式中：m为物体质量；V为物体运动速度；F为物体受到的力；M 为所受力矩；I为惯性矩；ω为角速度；弹体在惯性系下的位移分量分别用x、y、z表示；上标i和b分别为惯性系和体轴系；而下标a、e和g分别为物体受到的气动力、发动机推力和体积力；θ、和ψ分别为旋转弹的俯仰角、滚转角和偏航角；RB－I为体轴系到惯性系的过渡矩阵。

式（2）与式（3）为刚体动力学方程组，式（4）与式（5）为刚体运动学方程。在进行轨迹仿真时，方程右端项全部已知，因此式（2）～式（5）的求解属于常微分方程的初值问题，一般采用Adams预估校正法求解，本文采用的是一种改进的Adams预估校正法［24－25］。

图1给出了适合旋转弹问题的CFD／RBD耦合轨迹仿真流程［25］，主要分为非耦合计算（Uncoupled Mode）和耦合计算（Coupled Mode）2部分。非耦合计算的主要目的是提供合理的初始流场，它包括2个步骤：首先计算旋转弹只有平动的定常初始流场，然后使弹体以初始滚转角速度作固定角速度旋转，并计算弹体周围的非定常流场。当得到稳定周期性非定常流场时，可获得轨迹仿真初始时刻旋转弹所受的气动力和气动力矩。此时进入耦合阶段，将初始时刻的气动力与力矩传递至刚体六自由度方程中的动力学方程以获得弹体对气动力的响应，例如平动和旋转加速度信息，再通过刚体运动学方程计算出平动速度、转动速度和欧拉角等，进而确定弹体在下一时刻的运动姿态。根据这些姿态信息，调整计算网格，进行下一时刻的CFD计算获取新的气动力，并代入刚体动力学方程求取新的弹体运动位置和姿态。重复以上耦合过程，直到满足终止条件仿真结束。

1．2 ARMA时域建模方法

ARMA时域建模方法可以通过系统参数辨识技术构建多输入多输出系统的降阶模型，该模型的数学表达通式为

式中：y（k）为输出参数，表示第k时间步的气动力参数矢量；ζ为该系统的输入参数；Ai和Bi为待辨识的系数矩阵；na和nb为输出和输入的延迟阶数，气动力的非定常效应也由此体现。

当样本数量大于Ai和Bi中所有未知参数的总数时，式（6）就表现为矛盾方程组，可采用最小二乘法求解，进而确定气动力模型的待定系数。下面以旋转弹的气动力建模为对象，具体介绍自回归滑动平均模型的辨识方法。

在旋转弹的气动力建模问题中，选取阻力Fxa、侧向力Fya、法向力Fza、滚转力矩 Mx、偏航力矩My和俯仰力矩Mz作为输出参数，模型系统的输入参数可以是弹体的运动速度和姿态角等状态量。但由于弹体在运动时本身具有强烈的角速度，这种运动状态会给弹体带来额外的气动力，因此，本文工作选用的输入参数还包含角速度。令Fn表示任一输出参数，Sn＝［unvnwnψn数，这里上标n为时间域上的样本编号，ωbx、ωby和ωbz分别为弹体绕体轴系x轴、y轴和z轴的旋转角速度。数值试验表明，旋转弹的模型系统中取延迟阶数na＝nb＝3时较为合适，于是式（6）可写为方程式（7）可以写为以下的矩阵形式：

当样本数目n＞30时，式（8）中未知参数数量少于方程总数。对矛盾方程组式（8）用最小二乘算法求解获得Ai和Bi，并代入式（7）即可确定ARMA气动力模型表达式。

建立好旋转弹的ARMA气动力模型后，利用其代替非定常CFD计算模块与刚体六自由度方程按图1所示的流程进行耦合，即可实现旋转弹的飞行轨迹仿真。

2 应用算例

选取美国陆军实验室超声速尾翼旋转弹自由飞行试验模型考察本文数值方法的正确性。该旋转弹模型由拱形－圆柱－尾翼3部分组成，尾翼呈十字型。图2给出了该模型的几何尺寸、质量和转动惯量等参数，cg代表重心位置。由于弹体外形轴对称，因此Ixy＝Ixz＝Iyz＝0。自由飞行试验过程中，旋转弹模型由炮筒打出，初期伴随着高速旋转［5］，但十字型尾翼的存在使得弹体在飞行时转速急剧下降。由于旋转弹在飞离炮筒的短时间内非定常效应显著，因此本文工作集中于精确捕捉弹体在这一时段伴随转速快速下降的姿态与飞行轨迹。

CFD计算采用如图3所示的非结构混合网格，附面层网格使用三棱柱型单元，其他区域采用四面体型单元。全套网格包含20 816个三角形表面网格单元、348 609个网格节点和811 923个体网格单元。依据文献［3］公布的自由飞行试验状态，设定旋转弹模型飞行的初始条件如表1所示，其对应的初始飞行马赫数为3．0，雷诺数为7．08×107／m，初始迎角为5°，弹体初始转速为2 518．39rad／s。

依据上述旋转弹初始发射条件，按图1中给出的轨迹仿真流程，对弹体飞行轨迹进行CFD／RBD耦合计算，获取旋转弹飞行过程中的非定常气动力（矩）参数和飞行状态参量，形成气动力建模的样本空间。

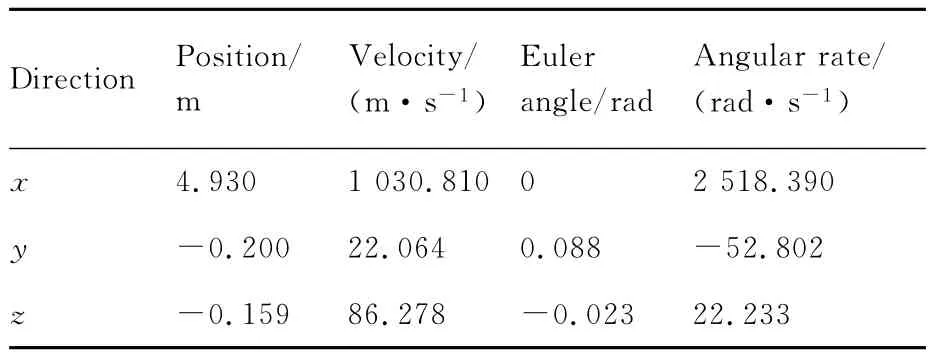
表1 弹体六自由度运动初始条件Table 1 Initial conditions of projectile in 6－DOF motion

2．1 气动力模型的建立与初步验证

在气动力建模时，以CFD／RBD耦合计算结果作为样本提供Fn和Sn，通过建立和求解方程组式（7）进行ARMA气动力建模。旋转弹的滚转角与其他飞行状态量（侧滑角、俯仰角、速度、角速度）相比，在量值与变化规律上存在特殊性。在保持其他输入参量不变的情况下，本文对滚转角采用了如图4所示的3种不同处理方式进行建模，并对建模效果进行了对比验证，横坐标xg为弹体质心在x方向的位移。为表述方便，以累积量（见图4（a））作为模型滚转角输入量建立的气动力模型称为模型A；以介于0°～360°范围内变化的滚转角（见图4（b））建模的气动力模型称为模型B；以滚转角正弦值的100倍（见图4（c））作为滚转角输入量建立的气动力模型称为模型C。用3种ARMA气动力模型代替非定常CFD计算模块分别与刚体六自由度模块耦合进行轨迹仿真。图5与图6中给出了3种模型获得的仿真结果与CFD／RBD耦合计算结果对比情况。

图5中，CFD／RBD耦合计算仿真得到的结果能够与试验值较好的吻合，说明了样本数据具有很高的置信度。而图5和图6中3种气动力模型代替CFD计算的仿真结果也都与CFD／RBD计算结果有很高的重合度，说明了这3种ARMA模型都可以很好地反映建模样本的非定常气动力特性。

2．2 不同初始发射条件下的轨迹仿真

在旋转弹设计过程中，往往需要考察初始转速或初始迎角的变化对其飞行轨迹的影响规律。因此，有必要考察先前建立的3种ARMA气动力模型在不同初始运动状态之下的适用性和精度。图7展示了利用CFD／RBD耦合的方法仿真得到的不同初始转速和初始迎角下弹体所受侧向力的变化历程。图中显示：随着初始转速和初始迎角的变化，弹体所受侧向力有明显改变。

为此，将初始滚转角速度ω0由2 518．39rad／s变为2 000rad／s，分别运用先前建立的3种ARMA模型与刚体六自由度耦合模块进行轨迹仿真，并与CFD／RBD耦合计算进行对比。图8给出了计算结果的对比情况，图中采用模型A仿真计算得到的阻力Fxa、滚转角、俯仰角速度ωby和偏航角速度ωbz等与CFD／RBD模拟的结果相比有显著区别，这说明该模型在变换初始滚转速度时已不能精确反映弹体的气动力（矩）参数。相反，对于以周期形式的滚转角作为输入量建立的非定常气动力模型B与模型C，其用于轨迹仿真的结果可以保持与CFD／RBD耦合计算结果较好地吻合。除阻力存在微小偏差，其余气动力（矩）以及六自由度状态量都与CFD／RBD轨迹仿真的结果高度一致。这说明在改变初始转速的情况下模型B与模型C依旧保持了良好的精度。

利用模型B和C与刚体六自由度方程耦合，将初始俯仰角由5°变为3°，再次进行轨迹仿真并与CFD／RBD耦合计算的结果在图9中进行对比。图中可见，初始俯仰角变化后，利用模型B或C与刚体六自由度方程耦合仿真依旧能得到与CFD／RBD一致度较好的结果。这再一次验证了本文所建立的ARMA气动力模型比较准确地反映了旋转弹的非定常气动特性，可以代替CFD非定常流场计算，与RBD方程耦合实现较高精度的飞行轨迹预测。

就计算效率而言，在一台主流微型计算机上采用CFD／RBD数值方法按照图1的耦合流程，仿真本文采用的旋转弹在某一初始条件下的运动轨迹大约需上百个机时。在此基础上获取ARMA气动力模型之后，如果要考察初始飞行条件发生小范围变化时的飞行轨迹，只需要CFD／RBD计算获得3个初始时刻仿真信息的基础上进行几秒钟机时的ARMA／RBD仿真即可。因此，与CFD／RBD耦合方法相比，运用 ARMA／RBD轨迹仿真可以显著地提升计算效率。

3 结 论

1）本文采用了一种自回归滑动平均（ARMA）的时域气动力建模方法对旋转弹自由飞行的气动力进行建模，并成功将ARMA气动力模型与刚体六自由度模块耦合，实现了多种初始发射状态下的弹体轨迹快速仿真。考察了滚转角的输入参数形式分别为累积量和周期量时，对轨迹仿真精度的影响，发现累积量作为气动力模型输入参数会带来较大的误差，滚转角以周期量的形式参与建模可以取得较好的模型精度。

2）算例表明：不论是在初始转速改变还是在初始俯仰角改变情况下，采用周期形式的输入量建立的ARMA气动力（矩）模型与刚体动力学方程耦合都能获得很高的轨迹仿真精度。说明了在初始条件变化不大的情况下，ARMA／RBD轨迹仿真方法可以部分替代CFD／RBD过程，从而缩短轨迹仿真时间，节省计算资源。

本文采用的ARMA时域建模本质上是一种线性气动力建模方法，它适合在气动力（矩）线性变化范围内使用，不能对大迎角等非线性特征很显著的气动力问题进行精确建模。如何进一步扩展气动力模型的适用范围，这将是作者今后研究工作的方向。

［1］ 苗瑞生，吴甲生．旋转弹空气动力学［J］．力学进展，1987，17（4）：992－1000．MIAO R S，WU J S，Aerodynamics of spinning projectile［J］．Advances in Mechanics，1987，17（4）：992－1000 （in Chinese）．

［2］ KANDEBO，STANLEY W．New powerplant key to missile demonstrator［N］．Aviation Week，2002，Sept．2．

［3］ SCOTT M，MURMAN，MICHAEL J，et al．Simulation of 6－DOF motion with a cartesian method：AIAA－2003－1246［C］／41st AIAA Aerospace Science Meeting．Reston：AIAA，2003．

［4］ SAHU J．Time－accurate numerical prediction of free－flight aerodynamics of a finned projectile：AIAA－2005－5817［C］／AIAA Atmospheric Flight Mechanics Conference and Exhibit．Reston：AIAA，2005．

［5］ SUHU J．Time－accurate numerical prediction of free－flight aerodynamics of a finned projectile［J］．Journal of Spacecraft and Rockets，2008，45（5）：946－954．

［6］ SAHU J．Time－accurate computations of free－flight aerodynamics of a spinning projectile with and without flow control：AIAA－2006－6006［C］／AIAA Atmospheric Flight Mechanics Conference and Exhibit．Reston：AIAA，2006．

［7］ 高庆丰，夏群力，方蜀州，等．基于非旋弹体坐标系的面对称旋转导弹六自由度弹道模型［J］．弹箭与制导学报，2010，30（4）：149－152．GAO Q F，XIA Q L，FANG S Z，et al．Six degree offreedom trajectory model of plane symmetry rolling missiles based on non－spinning body coordinate system［J］．Journal of Projectiles Rockets Missiles and Guidance，2010，30（4）：149－152（in Chinese）．

［8］ 孙海生，张海酉，刘志涛．大迎角非定常气动力建模方法研究［J］．空气动力学学报，2011，29（6）：733－737．SUN H S，ZHANG H Y，LIU Z T．Comparative evaluation of unsteady aerodynamics modeling approaches at high angle of attack［J］．Acta Aerodynamica Sinica，2011，29（6）：733－737（in Chinese）．

［9］ LIN G F，LAN C E．A generalized aerodynamic coefficient model for fight dynamics application：AIAA－1997－3643［R］．Reston：AIAA，1997．

［10］ 姜久龙，李学仁，杜军，等．飞机纵向非定常气动力建模与辨识［J］．空军工程大学学报（自然科学版），2013，14（4）：14－18．JIANG J L，LI X R，DU J，et al．The study of modeling and identification of longitudinal unsteady aerodynamics［J］．Journal of Air Force Engineering University（Natural Science Edition），2013，14（4）：14－18（in Chinese）．

［11］ GOMAN M，KHRABROV A．State－space presentation of aerodynamic characteristic of an aircraft at high angle of attack：AIAA－1992－465［R］．Reston：AIAA，1992．

［12］ 汪清，何开锋，钱炜祺，等．飞机大攻角空间机动气动力建模研究［J］．航空学报，2004，25（5）：447－450．WANG Q，HE K F，QIAN W Q，et al．Aerodynamic modeling of spatial maneuvering aircraft at high angle of attack［J］．Acta Aeronautica et Astronautica Sinica，2004，25（5）：447－450（in Chinese）．

［13］ 汪清．飞机大迎角非定常气动力建模及应用研究［D］．西安：西北工业大学，1994：45－49．WANG Q．Modeling andapplication research of unsteady aerodynamic force of aircraft at high angle of attack［D］．Xi’an：Northwestern Polytechnical University，1994：45－49（in Chinese）．

［14］ 孔轶男．气动力建模的模糊逻辑方法［D］．绵阳：中国空气动力研究与发展中心，2005．KONG Y N．Fuzzylogic method for aerodynamic modeling［D］．Mianyang：China Aerodynamic Research and Development Center，2005（in Chinese）．

［15］ 龚正，沈宏良，吴根兴．非定常气动力对飞行动力学特性影响分析［J］．南京航空航天大学学报，2009，41（3）：291－295．GONG Z，SHEN H L，WU G X．Impact analysis of unsteady aerodynamic force on flight dynamics characteristics［J］．Journal of Nanjing University of Aerodynamics ＆Astronautics，2009，41（3）：291－295（in Chinese）．

［16］ 叶正寅，张伟伟，史爱明，等．流固耦合力学基础及其应用［M］．哈尔滨：哈尔滨工业大学出版社，2010．YE Z Y，ZHANG W W，SHI A M，et al．Foundation of fluid solid coupling mechanics and its application［M］．Harbin：Harbin Institute of Technology Press，2010 （in Chinese）．

［17］ SILVA W A，RAVEH D E．Development of unsteady aerodynamic state－space models from CFD－based pulse responses：AIAA－2001－1213［R］．Reston：AIAA，2001．

［18］ SILVA W A．Identification of linear and nonlinear aerodynamic impulse responses using digital filter techniques：AIAA－1997－3712［R］．Reston：AIAA，1997．

［19］ COWAN T J．Efficient aeroelastic CFD predictions using system identification［D］．Oklahoma：Oklahoma State University，1996．

［20］ COWAN T J，ARENA A S，GUPTA K K．Development of a discrete－time aerodynamic model for CFD－based aeroelastic analysis：AIAA－1999－0765［R］．Reston：AIAA，1999．

［21］ 李惠芝．旋转弹的气动布局与旋转效应［J］．现代防御技术，1990（6）：16－40．LI H Z．Theaerodynamic configuration and rotation effect of the rotating projectile［J］．Modern Defense Technology，1990（6）：16－40（in Chinese）．

［22］ 李臣明，刘怡欣．尾翼式旋转火箭的弹道散布仿真分析［J］．兵工自动化，2012，31（12）：1－4．LI C M，LIU X Y．Simulation andanalysis on ballistic dissemination of rocket with empennage［J］．Ordnance Industry Automation，2012，31（12）：1－4（in Chinese）．

［23］ 王刚，叶正寅．三维非结构混合网格生成与N－S方程求解［J］．航空学报，2003，24（5）：385－390．WANG G，YE Z Y．Generation of three dimensional mixed and unstructured grids and its application in solving Navier－Stokes equations［J］．Acta Aeronautica et Astronautica Sinica，2003，24（5）：385－390（in Chinese）．

［24］ 蒋跃文，叶正寅，张伟伟．一种半隐式的气动弹性时域求解办法［J］．工程力学，2012，29（4）：66－71．JIANG Y W，YE Z Y，ZHANG W W．Semi－implicit solution of aeroelastic equations in time domain［J］．Engineering Mechanics，2012，29（4）：66－71（in Chinese）．

［25］ WANG G，ZENG Z，SUO Q．Trajectory simulation of a spinning projectile based on variable step size CFD／RBD method：AIAA－2015－0522［C］／AIAA Atmospheric Flight Mechanics Conference．Reston：AIAA，2015．

Aerodynamic modeling and flight trajectory simulation of spinning projectile

WANG Gang＊，XING Yu，ZHU Ya’nan
School of Aeronautics，Northwestern Polytechnical University，Xi’an 710072，China

A time－domain autoregressive moving average（ARMA）method for aerodynamic modeling is adopted in the spinning projectile six－degree of freedom trajectory simulation．The computational fluid dynamics coupled with rigid body dynamics equations（CFD／RBD）simulation result is regarded as sample，and the unsteady aerodynamic model of the spinning projectile is established successfully．Different forms of the unsteady aerodynamic model combined with RBD equations are discussed considering the influence on the simulation effect．As is shown in the result，appropriate modeling form combined with RBD module can simulate the motion and attitude of the spinning projectile，and the simulation results from the new approach can fit well with CFD／RBD results under different initial conditions．This new simulation approach can be applied to the fast simulation research，which can not only guarantee the precision，but also save much time and computing resources compared with CFD／RBD simulation method．

autoregressive moving average；aerodynamic modeling；rigid－body dynamics；unsteady aerodynamic；trajectory simulation

2016－02－26；Revised：2016－05－09；Accepted：2016－05－26；Published online：2016－06－02 10：13

V212

A

1000－6893（2017）01－120169－10

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

10．7527／S1000－6893．2016．0169

2016－02－26；退修日期：2016－05－09；录用日期：2016－05－26；网络出版时间：2016－06－02 10：13

www．cnki．net／kcms／detail／11．1929．V．20160602．1013．002．html

＊通讯作者 ．E－mail：wanggang＠nwpu．edu．cn

王刚，邢宇，朱亚楠．旋转弹气动力建模与飞行轨迹仿真［J］．航空学报，2017，38（1）：120169．WANG G，XING Y，ZHU Y N．Aerodynamic modeling and flight trajectory simulation of spinning projectile［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：120169．

（责任编辑：李明敏）

URL：www．cnki．net／kcms／detail／11．1929．V．20160602．1013．002．html

＊Corresponding author．E－mail：wanggang＠nwpu．edu．cn