基于鲁棒伺服LQR的结冰飞机纵向控制律重构方法

陈威，徐浩军，王小龙，裴彬彬，李哲

基于鲁棒伺服LQR的结冰飞机纵向控制律重构方法

陈威，徐浩军＊，王小龙，裴彬彬，李哲

空军工程大学 航空航天工程学院，西安 710038

由于防／除冰系统总会出现故障或者除冰不彻底，因此仅依靠防／除冰系统实现结冰条件下的安全飞行并非完全可靠，研究结冰后飞机控制律重构对飞机操纵安全和飞行安全极其重要。针对飞机的纵向运动建立了结冰影响模型和纵向动力学模型，采用鲁棒伺服线性二次型调节器（LQR）最优控制设计了飞机结冰后空中飞行纵向控制律，模拟了飞机在俯仰姿态保持模式下遭遇不同严重程度结冰后的动态响应特性，并与常规PID控制进行对比。结果表明，所设计的控制律能够有效改善结冰飞机的飞行性能和飞行品质，准确跟踪给定的俯仰角指令，且抗干扰能力、动态性能以及鲁棒性均优于常规PID控制。为飞机结冰后的重构控制问题和自动飞行控制，提供了新的思路。

飞机结冰；鲁棒伺服LQR；纵向运动；控制律重构；仿真验证

飞机结冰是飞机在结冰气象条件下飞行时，大气中的液态水在部件表面冻结并累积成冰的一种物理过程，是飞行实践中广泛存在的一种现象［1］。飞机结冰后不仅会增加飞机的重量，还会改变飞机的气动外形而使飞行品质和飞行性能恶化。目前，结冰条件下的安全飞行主要是通过飞机上的防／除冰系统来实现。但是防／除冰系统总会出现故障，而且即使正常运行也不能保证完全除去冰层。因此，仅依靠防／除冰系统实现结冰条件下的安全飞行并非完全可靠，最根本的解决办法是根据飞机的结冰情况重新设计适当的飞行安全保障方法［2］。控制律重构是保证飞机安全飞行的一种途径，目前用于实现飞机控制律重构的方法较多，如H∞控制、自适应控制、线性二次型调节器（Linear Quadratic Regulator，LQR）以及神经网络控制技术等［3－6］，而深入研究飞机结冰以后控制律重构的文献还不多见。

美国伊利诺州大学的Bragg等提出了飞机智能 防 冰 系 统 （Smart Icing System，SIS）的 设想［7］，为飞机容冰控制提供了思路。Hossain等［8］运用自适应控制技术，研究了飞机结冰后的包线保护算法。Sharma等［9］运用线性矩阵不等式方法，分析了结冰条件下系统的二次稳定性，并探讨了如何将迎角维持在失速范围之内。Aykan等［10－11］利用神经网络、卡尔曼滤波、容错控制等技术，研究了飞机结冰问题的识别检测和控制律重构等。

由于缺乏传统研究方法的积累，国内的相关研究工作还处于起步阶段。南京航空航天大学的张智勇［12］对人工驾驶和自动驾驶两种情况的飞行包线保护控制律进行了研究。北京航空航天大学的杜亮和洪冠新［13］分析了结冰对飞行包线的影响，并通过实时地改变可用飞行包线范围，保证飞机在结冰条件下的飞行安全。复旦大学的应思斌和艾剑良［14－15］基于飞机容冰飞行控制技术，建立了综合结冰保护系统。空军工程大学的周莉［2］基于线性矩阵不等式分别设计了飞机状态反馈保性能控制律和输出反馈保性能控制律，以此保障飞机结冰后的飞行安全。

从现有公开发表的文献看，国内外针对结冰条件下的重构控制问题的研究成果还比较少，这也从侧面反映了这方面的研究基础相对薄弱。因此，深入研究和探讨结冰条件下的控制律重构技术，对于提高结冰条件下的飞行操作性和安全性具有重大意义。在这样的研究背景下，本文基于鲁棒伺服LQR最优控制对结冰飞机纵向控制律进行了重构研究。鲁棒伺服LQR最优控制是在传统LQR控制的基础上，在控制回路中加入积分环节，把状态偏差作为新的变量引入到系统中，能够有效抑制外界扰动对系统的影响，同时保证系统的鲁棒性和动态性能。通过模拟飞机在俯仰姿态保持模式下遭遇不同严重程度结冰后的动态响应特性，并与常规PID控制进行对比，验证了该控制方法的优越性，具有一定的工程应用价值。

1 模型简述

1．1 结冰影响模型

飞机结冰后，其气动参数可利用以下模型进行计算［16］：

式中：C（A）为结冰前飞机某一气动参数；C（A）iced为结冰后该气动参数值；KCA为结冰系数，反映C（A）由于结冰所引起的变化量，对于给定的飞机为常值；η为飞机结冰因子，η∈［0，1］表征了不同气象条件下的结冰严重程度。结冰系数KCA的取值如表1所示［17］。表中CL0为迎角为零时的升力系数；CLα为升力线斜率；CLq为升力系数对俯仰角速率的偏导数；CLδe为升力系数对升降舵偏角的偏导数；Cm0为飞机零升力矩系数；Cmα为纵向静稳定导数；Cmq为俯仰力矩系数对俯仰角速率的偏导数；Cmδe

为升降 舵操纵导 数；CYβ为侧力导数；CYδr为方向舵侧力导数；Clβ为横向静稳定导数；Clp为滚转阻 尼导数 ；Clδa为滚转操纵导数；Clδr为 方 向 舵操纵交叉导数；Cnβ为航向静稳定性导数；Cnr为航向阻尼导数；Cnδa为副翼操纵交叉导数。

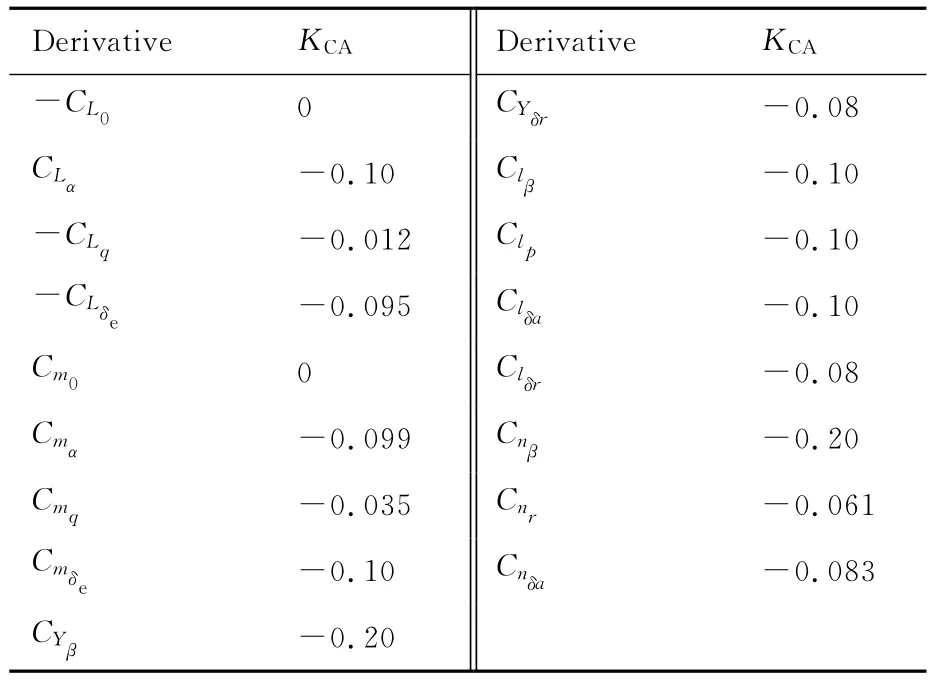
表1 飞机气动导数的结冰系数［17］Table 1 Icing coefficients of aircraft aerodynamic derivative［17］

该结冰影响模型是Bragg等［16］对NASA“双水獭”飞机结冰飞行试验数据进行拟合分析得到的。Lampton和Valasek［17］将其应用于“塞斯纳”飞机结冰飞行动力学特性研究，并通过试飞验证了模型的适用性和正确性。本文研究的背景飞机与“双水獭”飞机气动布局相似，因此可采用该结冰影响模型对本文背景飞机的结冰后气动参数进行计算。

1．2 纵向动力学模型

飞机的纵向自动驾驶仪包括俯仰姿态保持、速度保持、高度保持等。其中俯仰姿态保持作为高度保持和某些速度保持的内回路，其性能直接影响飞机的飞行品质，因此俯仰姿态保持是纵向控制的关键。本文主要是针对飞机俯仰姿态保持的结冰后控制律重构方法进行研究。

本文主要考虑飞机的纵向动力学模型，其纵向六自由度非线性方程组表示为［18］

1）位移变化速率

式中：u、v、w为飞机飞行速度在体轴系上的分量；θ、、ψ分别为俯仰角、滚转角和偏航角；xg、zg为飞机在地面坐标系的位移。

2）角位移变化速率

式中：q和r分别为俯仰角速率和偏航角速率。

3）速度变化速率

式中：p为滚转角速率；X、Z为飞机受到的气动力在体轴系上的分量；m为飞机的质量；g为重力加速度。

机体坐标系与速度坐标系间速度转换关系为

式中：V为飞机空速；α为飞机的迎角；β为飞机的侧滑角。

力和力矩方程为

式中：M 为 俯仰力矩；Ix、Iy、Iz为飞 机对Oxb、Oyb和Ozb轴的转动惯量；Ixz为飞机对Oxb与Ozb轴的惯性积。

以飞机的定常直线无侧滑飞行作为基准运动，利用小扰动方法将非线性模型线性化，得到其纵向运动线性模型。纵向运动状态空间表达式为

式中：x＝［V α q θ H］T为状态变量，H 为飞行高度；y＝［V α q θ H］T为输出变量；u＝ ［δeδT］T为控制变量，δe和δT分别为升降舵偏 角 和 油 门 杆 位 置；A∈R5×5、B∈R5×2、C＝diag ｛1，1，1，1，1｝ 分别为状态矩阵、控制矩阵和输出矩阵。

在结冰条件下，状态矩阵和控制矩阵会出现摄动，且变化量受飞机结冰因子η的影响。

2 纵向控制律设计

近年来，鲁棒控制理论和飞行控制技术得到了快速的发展。当飞机在空中遭遇结冰后，如果已经确定结冰对飞机飞行性能以及操稳特性的影响程度，可以运用鲁棒控制理论重构合理的空中飞行控制律供飞行控制系统进行自动调整，使飞机在安全边界内按照预定的航线飞行，保证结冰条件下的飞行安全。

基于此，本文采用鲁棒伺服LQR最优控制方法对结冰后飞机纵向控制律进行重构，以保障结冰飞机的安全性。

2．1 纵向飞行品质要求

飞机纵向控制中，短周期响应往往时间短、变化迅速，飞行员难以进行有效操纵；而长周期响应一般变化缓慢，飞行员有足够的时间进行操纵控制。因此，大多数纵向飞行品质准则是针对短周期响应进行的［19］。

本文背景飞机为某轻型运输机，根据文献［18］，其纵向飞行品质要求如表2所示。表中tr为上升时间；σ为超调量；ess为稳态误差；ts为调节时间；ζsp短周期阻尼比。

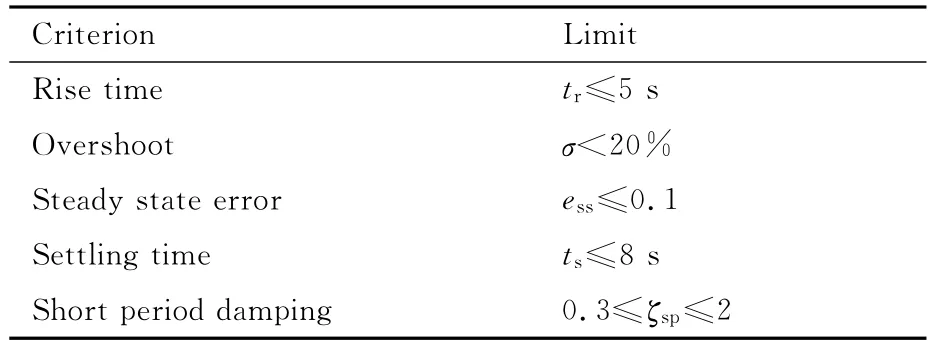
表2 纵向飞行品质要求［18］Table 2 Longitudinal flight quality requirements［18］

2．2 鲁棒伺服LQR最优控制方法

对于式（10）系统状态方程，传统LQR控制方法要求确定控制律u，使式（11）表示的性能指标函数最小［20］。

式中：Q＝QT，为性能加权矩阵；K＝KT，为控制加权矩阵。

最优控制律由式（12）给出。

式中：Z为控制增益矩阵。

黎卡提方程如式（13）所示，对称矩阵P是其半正定解。

由式（12）和式（13）可知，K和Q 的选取直接影响控制系统的控制效果。在确定K和Q时，由于两者有相对比例关系，可以令K＝I，通过迭代运算选取满足指标要求的性能加权矩阵Q，并最终得出最优的控制律。

鲁棒伺服LQR最优控制方法是在传统LQR控制方法的基础上发展起来的，它的思想是将积分环节引入到控制律的前向回路中，把状态偏差量定义为新的状态向量引入到系统中，增强控制器对扰动的适应能力，使系统具备准确跟踪输入控制指令的能力［21］。

设系统要跟踪的输出为yc，yc＝Ccx，跟踪误差表示为e＝r－yc，将其定义为新的状态变量，则新系统的状态方程为

此时式（14）所示新系统的性能指标函数为

新系统的黎卡提方程为

通过设计适当的K阵和Q阵，解黎卡提方程（16），可得控制增益矩阵为

由于μ＝u，μ＝－Zz，则控制输入表达式为

2．3 控制律设计

目前工程上常用的俯仰角控制器结构一般为PID控制器，其结构图如图1所示，控制器数学表达式为［12］

式中：kθ、ki和kq为控制器的增益。

本节主要基于鲁棒伺服LQR最优控制对纵向控制律进行设计。在控制律的设计过程中，不可能对包线范围内的每一种配平状态都进行设计，只可能选取一种或几种典型的易结冰飞行状态进行设计，

使其兼顾到所有的状态。控制律初步设计完成后，在给定的平衡点处对其进行检验和调整，直至满足指标要求为止。

根据联邦航空条例25部（FAR－25）附录C—大气结冰条件，典型易结冰初始飞行条件设定为：H＝3 000m，V＝100m／s［22］。

2．3．1 俯仰角速率控制器设计

为设计俯仰角速率回路控制器，从纵向运动线性模型式（10）中提取状态x＝q，y＝q。在H＝3 000m、V＝100m／s初始飞行条件下，依据η＝1时的最严重结冰情况，得到背景飞机的Ac＝－0．675 3，Bc＝－1．855 1，Cc＝1。

选取输出信号为俯仰角速率q，则跟踪误差表示为

式中：qref为俯仰角速率指令。

将跟踪误差e定义为系统新的状态变量，得到新的状态方程为

于是控制输入表达式为

根据式（22）可以得到俯仰角速率控制器的结构如图2所示。

俯仰角速率控制器的数学表达式为

2．3．2 俯仰角控制器设计

俯仰角控制是在俯仰角速率控制器的基础上进行设计，为了使其达到较高的精度，俯仰角控制回路采用比例积分控制。俯仰角控制器的结构如图3所示。

俯仰角控制器的数学表达式为

式中：θref为俯仰角指令；Zθ1和Zθ2分别为俯仰角控制回路的积分系数和比例系数。

由式（24）可得

通过对式（25）进行拉氏变换，得到俯仰角控制器的传递函数为

由式（26）可知，俯仰角控制器的传递函数可近似看成是二阶低通环节，自然频率为，阻尼比为／（2），积分系数和比例系数Z可根据内外环带宽匹配关系以及最佳阻尼比原则进行确定［20］。对于本文的背景飞机，可得＝0．04，Z＝0．28。

3 仿真验证与分析

以某轻型运输机为研究对象，利用本文所构建的结冰影响模型和纵向运动线性模型，在不同结冰严重程度下对所设计的俯仰角控制器进行仿真，并与常规PID俯仰角控制器进行对比。

初始飞行条件为：H＝3 000m，V＝100m／s，飞机结冰严重程度依次为η＝0，0．3，0．5，0．7，1．0。

3．1 飞机结冰后的动态响应特性

飞机初始状态为平飞状态，0s出现不同严重程度的结冰。为研究飞机遭遇不同严重程度结冰后的动态响应特性，在仿真的过程中并没有加入驾驶员的修正操纵，图4为未采用控制器情况下飞机结冰后的动态响应曲线。

从图4可以看出，未结冰飞机（η＝0）始终处于平飞状态，结冰后的响应曲线出现振荡，随着η值的增大，振幅逐渐增大，并且衰减较慢，导致振荡的持续时间逐渐增大，可见结冰使飞机平飞性能下降。尤其在η＝1时，飞机高度H在100s内下降100m，飞机迎角α的极值达到15．2°，大于失速迎角，飞机很容易失稳或发生危险。为保证飞机在安全边界内按照预定的航线飞行，适当的控制方法非常必要。

3．2 基于鲁棒伺服LQR控制器仿真

飞机初始状态为平飞状态，1s出现不同严重程度的结冰，图5为基于鲁棒伺服LQR控制的俯仰角速率控制器阶跃响应曲线。

表3为基于鲁棒伺服LQR控制的俯仰角速率控制器时域性能品质。

从图5和表3可以看出，在不同严重程度结冰条件下，俯仰角速率响应较快，稳态误差为零，

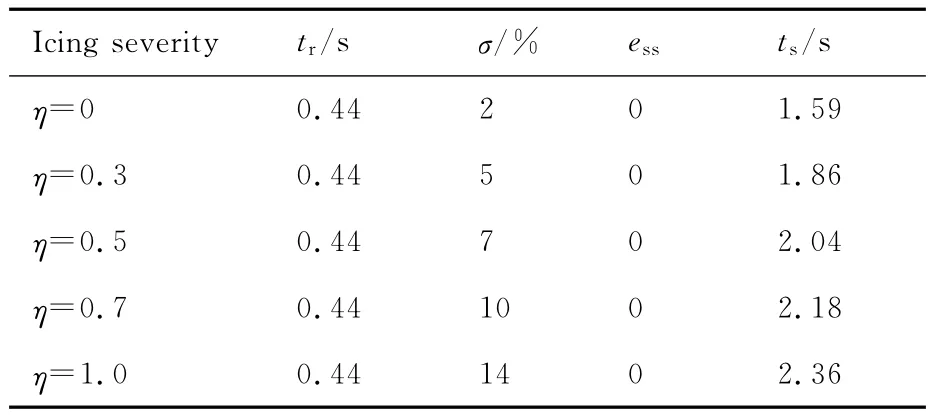
表3 俯仰角速率控制器时域性能品质Table 3 Performance quality of pitching angle rate controller in time domain

能实现对俯仰角速率的精确跟踪。随着η的增大，超调量和调节时间逐渐增大，但仍符合性能品质要求。

飞机初始状态为平飞状态，仿真时输入俯仰角指令为8°，0s出现不同严重程度的结冰，图6为采用鲁棒伺服LQR控制后的状态参数响应曲线。

如图6（c）俯仰角响应曲线所示，在不同严重程度结冰条件下，该控制器均能无误差的跟踪给定的俯仰角指令，且响应速度较快。系统的超调量和调节时间随着结冰因子η的增大而逐渐增大，但仍在可接受范围之内。由图6（a）速度响应曲线和图6（b）高度响应曲线可知，飞机的爬升性能随结冰因子η的增大而逐渐恶化，由于未控制油门，速度V的损失也逐渐增大，但最终都趋于稳定。而由图6（d）～图6（f）可知，为确保飞机结冰时也能准确跟踪给定的参考指令，结冰越严重即η越大，迎角α稳态值越大，俯仰角速率q、升降舵偏角δe初期振荡越剧烈，但最终都能在短时间内达到稳态值。其中迎角α初始响应峰值为7．45°，最终稳定极值为6．7°，均远小于失速迎角。可见该控制器有效地抑制了结冰扰动的影响，且鲁棒性与动态性能优越。

3．3 鲁棒伺服LQR控制与PID控制对比

飞机初始状态为平飞状态，仿真时输入俯仰角指令为8°，针对未结冰（η＝0）和最严重结冰（η＝1）进行仿真，图7和图8分别为η＝0和η＝1时采用鲁棒伺服LQR控制以及常规PID控制后的状态参数响应曲线。

表4为η＝0时鲁棒伺服LQR控制和常规PID控制作用下的俯仰角控制器时域性能品质。

由图7（c）俯仰角响应曲线和表4可知，在飞机未结冰（η＝0）情况下，两种控制律的控制效果均满足性能品质要求，都能准确地跟踪给定的俯仰角指令，但鲁棒伺服LQR控制稳态误差为0，跟踪更精确，比常规PID控制超调量减小66%，调节时间减小27%，且响应更平缓。由图7（a）速度响应曲线和图7（b）高度响应曲线可知，两种控制律作用下，高度H和速度V的变化几乎一致，爬升性能差别不大。而从图7（d）～图7（f）可知，俯仰角速率q、迎角α、升降舵偏角δe的最终稳态值相同，但PID控制在响应初期振荡幅度较大，且衰减相对较慢，尤其是升降舵偏角δe，在0．2s达到极值－15．7°，响应极不平稳。

表5为η＝1时鲁棒伺服LQR控制和常规PID控制作用下的俯仰角控制器时域性能品质。

如图8（c）俯仰角响应曲线和表5所示，飞机严重结冰（η＝1）后，俯仰角θ的初期振荡幅度和振荡持续时间均增大，两种控制律的动态性能和鲁棒性均变差，但仍满足性能指标要求，且鲁棒伺服LQR控制响应更平缓，可以无稳态误差地跟踪给定的参考指令，比常规PID控制超调量减小30%，调节时间减小17%。由图8（a）速度响应曲线和图8（b）高度响应曲线可知，结冰后速度V损失增大，高度H增量减小，爬升性能恶化，且两种控制律作用下的变化趋势一致。而从图8（d）～图8（f）可知，为确保结冰时也具有良好的跟踪性能，迎角α的稳态值增大，俯仰角速率q、升降舵偏角δe的初期振荡持续时间均增大，但均能在8s内恢复到原平衡状态。在鲁棒伺服LQR控制作用下，虽然升降舵偏角δe的后期振荡幅度略大于PID控制，但俯仰角θ响应比PID控制平缓，跟踪更精确，且PID控制作用下的升降舵偏角δe初期振荡幅度更剧烈，在0．24s达到极值－17．3°，响应极不平缓，使舵机瞬间产生较大过载，对飞机结构设计时的可用过载要求更高。

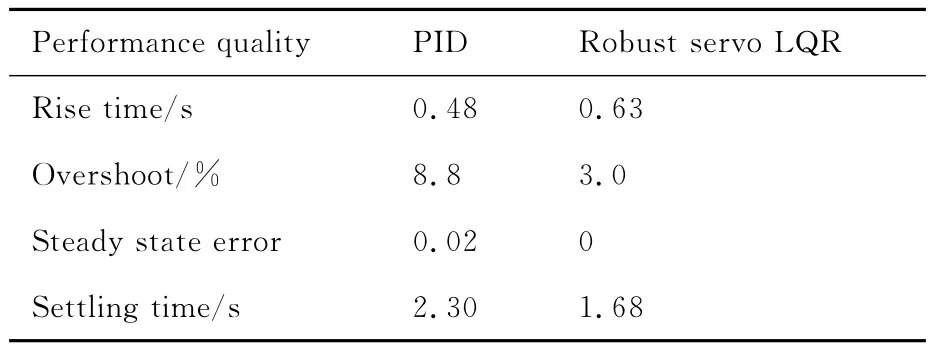
表4 俯仰角控制器时域性能品质（η＝0）Table 4 Performance quality of pitching angle controller in time domain（η＝0）

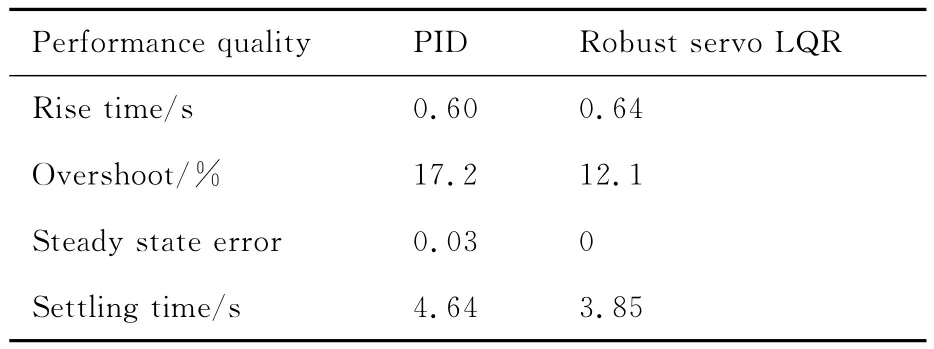
表5 俯仰角控制器时域性能品质（η＝1）Table 5 Performance quality of pitching angle controller in time domain（η＝1）

通过两种控制律在未结冰（η＝0）和严重结冰（η＝1）时的对比仿真可以发现，鲁棒伺服LQR控制在η＝0和η＝1时均能无稳态误差地跟踪给定的参考指令，鲁棒性能更优越，响应相对平稳，对结冰扰动的抑制效果好于PID控制，在超调量和调节时间等性能指标方面明显优于PID控制，动态性能更优异。

4 结 论

1）结冰的影响随着η的增大而增强，导致飞机飞行性能和飞行品质下降。尤其在严重结冰（η＝1）情况下，如果驾驶员不采取措施进行修复，飞机很容易失稳或发生危险。

2）在不同结冰严重程度下，本文所设计的控制律均具有良好的跟踪性，保证了系统的动态性能和鲁棒性，能有效改善结冰飞机的飞行性能和飞行品质，且抗干扰能力、动态性能以及鲁棒性优于常规PID控制。

3）控制律的控制效果随结冰因子η的增大而变差，但仍符合性能品质要求。研究结果可为结冰飞机的重构控制问题和自动飞行控制提供一定的参考和思路，具有一定的工程应用价值。

［1］ COLE J，STANDS W．Statistical study of aircraft icing accidents：AIAA－1991－0558［R］．Reston：AIAA，1991．

［2］ 周莉．结冰条件下的飞机性能与安全保障方法研究［D］．西安：空军工程大学，2012．ZHOU L．Study on methods for assuring aircraft flight performance and safety under icing conditions［D］．Xian：Air Force Engineering University，2012（in Chinese）．

［3］ 徐彦军，林正，孙岩，等．基于H∞控制的飞机俯仰角控制系统设计［J］．飞行力学，2010，28（6）：24－27．XU Y J，LIN Z，SUN Y，et al．Design of aircraft pitching angle control system based on H∞control［J］．Flight Dynamics，2010，28（6）：24－27（in Chinese）．

［4］ 刘小雄，章卫国，武燕，等．基于直接自适应控制的重构飞控系统研究［J］．控制与决策，2007，22（4）：440－444．LIU X X，ZHANG W G，WU Y，et al．Direct adaptive control－based reconfiguration flight control system［J］．Control and Decision，2007，22（4）：440－444 （in Chinese）．

［5］ 赵海，李振水，薛峰，等．纵向控制律的LQR设计及性能检验［J］．系统仿真学报，2009，22（4）：348－350．ZHAO H，LI Z S，XUE F，et al．LQR design and performance examination of longitudinal control law ［J］．Journal of System Simulation，2009，22（4）：348－350 （in Chinese）．

［6］ 张栋．基于神经网络的歼击机自修复飞行控制律重构［D］．南京：南京航空航天大学，2003．ZHANG D．The reconfiguration of the self－repairing flight control law for fighters using neural networks［D］．Nanjing：Nanjing University of Aeronautics and Astronautics，2003（in Chinese）．

［7］ BRAGG M B，PERKINS W R，SARTER N B，et al．An interdisciplinary approach to inflight aircraft icing safety：AIAA－1998－0095［R］．Reston：AIAA，1998．

［8］ HOSSAIN K N，SHARMA V，BRAGG M B，et al．Envelope protection and control adaptation in icing encounters：AIAA－2003－0025［R］．Reston：AIAA，2003．

［9］ SHARMA V，VOULGARIS P G，FRAZZOLI E．Aircraft autopilot analysis and envelope protection for operation under icing conditions［J］．Journal of Guidance，Control，and Dynamics，2004，27（3）：454－465．

［10］ AYKAN R，HAJIYEV C，CALISKAN F．Aircraft icing detection，identification and reconfigurable control based on Kalman filtering and Neral networks：AIAA－2005－6220［R］．Reston：AIAA，2005．

［11］ AYKAN R，HAJIYEV C，CALISKAN F．Kalman filter and Neural network－based icing identification applied to A340aircraft dynamics［J］．Aircraft Engineering and Aerospace Technology：An International Journal，2005，77（1）：23－33．

［12］ 张智勇．结冰飞行动力学特性与包线保护控律研究［D］．南京：南京航空航天大学，2006．ZHANG Z Y．Research on iced aircraft flight dynamics characteristics and envelope protection control law［D］．Nanjing：Nanjing University of Aeronautics and Astronautics，2006（in Chinese）．

［13］ 杜亮，洪冠新．结冰对飞机飞行包线影响分析及控制［J］．飞行力学，2008，26（2）：9－12．DU L，HONG G X．Analysis and control of icing effects on aircraft flight envelope［J］．Flight Dynamics，2008，26（2）：9－12（in Chinese）．

［14］ 应思斌，艾剑良．飞机结冰包线保护对开环飞行性能影响与仿真［J］．系统仿真学报，2010，22（10）：2273－2275．YING S B，AI J L．Simulation of aircraft flight envelope protect in icing encounters effects on open loop dynamic［J］．Journal of System Simulation，2010，22（10）：2273－2275（in Chinese）．

［15］ 应思斌．飞机容冰飞行控制系统设计的理论与方法研究［D］．上海：复旦大学，2010．YING S B．Study on the theory and methods of aircraft icing tolerant flight control system design［D］．Shanghai：Fudan University，2010（in Chinese）．

［16］ BRAGG M B，HUTCHISON T，MERRET J，et al．Effect of ice accretion on aircraft flight dynamics：AIAA－2000－0360［R］．Reston：AIAA，2000．

［17］ LAMPTON A．VALASEK J．Prediction of icing effects on the coupled dynamic response of light airplanes［J］．Journal of Guidance，Control，and Dynamics，2008，31（3）：656－673．

［18］ NELSON R C．Flight stability ＆automatic control［M］．2nd ed．New York：The McGraw－Hill Companies，1998：153－155．

［19］ 高金源，李陆豫，冯亚昌．飞机飞行品质［M］．北京：国防工业出版社，2003：143－145．GAO J Y，LI L Y，FENG Y C．Aircraft handling qualities［M］．Beijing：National Defense Industry Press，2003：143－145（in Chinese）．

［20］ 段镇．无人机飞行控制系统若干关键技术研究［D］．长春：中国科学院长春光学精密机械与物理研究所，2014．DUAN Z．Research on some key technologies of flight control system of UAV［D］．Changchun：Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，2014（in Chinese）．

［21］ WISE K A．Bank－to－turn missile autopilot design using loop transfer recovery［J］．Journal of Guidance，Control，and Dynamics，1990，13（1）：145－152．

［22］ Federal Aviation Administration．Part 25－airworthiness standards：transport category airplanes［S］．Washington，D．C．：Federal Register，1990：58－60．

Reconfigurable control methods of icing aircraft longitudinal motion based on robust servo LQR

CHEN Wei，XU Haojun＊，WANG Xiaolong，PEI Binbin，LI Zhe
College of Aeronautic and Astronautic Engineering，Air Force Engineering University，Xi’an 710038，China

Anti－icing and de－icing system could not ensure flight safety under icing condition all the time due to the unreliability of it，research focus on reconfigurable flight control for ice tolerance is significant．The icing effect model and longitudinal dynamic model are established．Based on robust servo linear quadratic regulator（LQR），the longitudinal flight control law is designed for icing aircraft，and then employed to study the dynamic response characteristics to different icing severity with pitch attitude hold，which validates the performance of the designed control law．Moreover，compared to the PID control，the result shows that the designed control law can improve the icing aircraft’s flight performance and qualities，and track the pitch instructions excellently．In addition，the anti－jamming capability，dynamic performance and robustness are better than PID control．The proposed methodology can give a theoretical support for reconfigurable control and automatic flight control design under icing conditions．

aircraft icing；robust servo LQR；longitudinal motion；reconfigurable control；simulation validation

2016－01－28；Revised：2016－03－04；Accepted：2016－03－16；Published online：2016－03－23 14：11

URL：www．cnki．net／kcms／detail／11．1929．V．20160323．1411．002．html

s：National Natural Science Foundation of China （61374145，U1333131）；National Basic Research Program of China（2015CB755802）

V212

A

1000－6893（2017）01－120129－10

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

10．7527／S1000－6893．2016．0087

2016－01－28；退修日期：2016－03－04；录用日期：2016－03－16；网络出版时间：2016－03－23 14：11

www．cnki．net／kcms／detail／11．1929．V．20160323．1411．002．html

国家自然科学基金 （61374145，U1333131）；国家“973”计划 （2015CB755802）

＊通讯作者 ．E－mail：xuhaojun＠xjtu．edu．cn

陈威，徐浩军，王小龙，等．基于鲁棒伺服LQR的结冰飞机纵向控制律重构方法［J］．航空学报，2017，38（1）：120129．CHEN W，XU H J，WANG X L，et al．Reconfigurable control methods of icing aircraft longitudinal motion based on robust servo LQR［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：120129．

（责任编辑：李明敏）

＊Corresponding author．E－mail：xuhaojun＠xjtu．edu．cn