一种基于动模态分解的翼型流动转捩预测新方法

韩忠华，王绍楠，韩莉，刘方良，许建华，宋文萍

一种基于动模态分解的翼型流动转捩预测新方法

韩忠华＊，王绍楠，韩莉，刘方良，许建华，宋文萍

西北工业大学 航空学院 翼型／叶栅空气动力学国家级重点实验室，西安 710072

考虑自由转捩的定常／非定常流动Navier－Stokes方程数值求解，对于翼型流动细节的精确模拟和气动力的精确预测均具有十分重要的意义。采用动模态分解（DMD）方法进行流动稳定性分析，再结合eN方法，提出了一套适用于翼型绕流的转捩预测新方法，称为DMD／eN方法。相比于传统的线性稳定性分析方法，DMD方法不需要求解附面层方程和线性稳定性方程，也没有引入平行流假设，具有更好的理论适用性和算法鲁棒性。开展了NLF0416、S809和SD7003等翼型的转捩预测数值验证研究，通过与实验结果以及与传统的基于线性稳定性分析的eN方法的比较，验证了本文所发展的转捩预测新方法在预测翼型的定常流动和非定常流动转捩方面的正确性，也表明了该方法具有解决含层流分离泡的翼型绕流转捩预测的能力。

转捩预测；动模态分解；eN方法；翼型；计算流体力学

流动由层流转变成湍流的过程称为转捩，转捩现象普遍存在于流体流动中［1］。高雷诺数下的机翼、大前缘半径的风力机叶片、高空螺旋桨和微型飞行器等的表面流动都存在转捩现象。由于影响因素众多、物理机理复杂，转捩问题一直是流体力学中尚未完全解决的前沿问题之一［2］。层流和湍流两种流态下物体表面的摩擦阻力、热传导速率和流动分离位置等特性大为不同，故转捩位置直接影响飞行器气动力计算的精确性，其中对阻力预测的影响尤为显著。因此，发展定常／非定常流动的转捩预测方法，对于飞行器流动细节的精确模拟和气动力的准确预测均具有十分重要的意义。

近年来，随着计算机技术的高速发展，大涡模拟（LES）和直接数值模拟（DNS）被应用于转捩研究［3－5］。但由于其计算量过于庞大，只能用于低雷诺数平板和翼型的研究，仍不适合工程应用。目前工程上常用的转捩预测方法主要有基于雷诺平均的湍流／转捩模式和基于线性稳定性理论的eN方法。前者在近年来有了较快发展，具有代表性的是基于当地变量的Gamma－Theta转捩模型［6－7］，且在其基础上考虑横流的转捩预测方法［8］也有了一定进展。符松和王亮［9］发展的适用于超声速边界层转捩预测的k－ω－γ三方程模型，也成为超声速流动转捩研究的热点。尽管如此，较早提出的基于线性稳定性理论的eN方法仍是目前工程中最常使用的转捩预测方法。其广泛用于翼型／机翼的边界层转捩预测［10－11］。

相比于定常流动，非定常流动的转捩预测更加复杂。德国国家航空航天研究院 （DLR）的Krumbein等［12］将拓展的eN转捩预测方法与非定常流动的雷诺平均Navier－Stokes（RANS）方程相结合，并以做俯仰振荡翼型进行了算例验证。德国布伦瑞克工业大学的 Radespiel等［13－14］应用该方法，实现了低雷诺数下翼型非定常层流分离流动的转捩位置自动预测。在国内，将eN转捩预测方法应用于翼型、机翼绕流的非定常数值模拟研究并不多见。刘方良［15］通过直接求解Navier－Stokes方程为预测边界层转捩提供高精度解，将eN方法与非定常RANS求解器耦合，研究了低雷诺数螺旋桨翼型的流动特性。然而，传统的基于线性稳定性分析的eN转捩预测方法，不能预测转捩过程中非线性效应的影响；同时由于其建立在平行流假设的基础上，忽略了流动横向速度和流向参数的弱增长。

为了克服线性稳定性分析的缺点，PSE（Parabolized Stability Equations）方法［16－17］和全局稳定性分析方法［18］被提出。同时模态分解方法也逐渐成为稳定性分析和流场相干结构分析的有力工具。其中，本征正交分解［19－21］（Proper Orthogonal Decomposition，POD）方法和动模态分解［22］（Dynamic Mode Decomposition，DMD）方法是目前应用比较广泛的两种模态分解方法。

2010年，Schmid［22］在 Koopman分析［23］的基础上提出了动模态分解方法，随后便成为众多研究者研究的热点［24－25］。该方法的基本思想是直接从实验或数值模拟得到的流场中提取出流动的动态信息；它既可用来表征流动的全局稳定性和动力学特征，又可用来解释流场的物理流动机理。不同于POD方法的每个模态对应着多个频率，DMD方法可以提取出随着单一频率变化的空间模态，因而可以表征不同频率的扰动在流动中沿着空间方向的增长。同时，DMD适用于包含线性增长或衰减的复杂频率，这使得该方法可以分析和解决流动不稳定性问题。目前DMD已被应用于边界层流动的稳定性分析研究。但是，国内外还没有被应用于边界层转捩预测研究的报道。

本文在基于线性稳定性分析的eN方法基础上，提出了一种用DMD替代线性稳定性分析的转捩预测新方法，称为DMD／eN方法。运用该方法，开展了绕二维翼型的定常及非定常效应不显著的准定常流动的转捩预测方法研究，验证了该方法的可行性和正确性，以及在处理含层流分离泡转捩问题方面的能力。

1 翼型流场数据的动模态分解方法

这里简要介绍DMD方法的数值求解过程，详细理论推导及算法介绍参见文献［22］。DMD方法可分为时间DMD和空间DMD，两者主要是快照划分方向的不同。由于本文关心的是流动在空间方向的发展规律，且通过分析，空间DMD更适用于本文研究的转捩预测方法，因而下面主要介绍空间DMD方法。

首先，提取流场信息。将从实验或数值计算中获得的流场数据表示成如下快照序列的形式：

式中：n为快照数；vi为第i个抽样数据的流场信息，称为快照（Snapshots）；Vn1为流场快照形成的矩阵，下标和上标分别为起始和终止的流场快照编号。

空间DMD方法假设相邻两个快照之间的空间间隔（Δx）是相同的，故需要将原有计算网格的流场信息插值到新的等间距分布的DMD网格线上，从而获得所需的流场快照信息。本文用于稳定性分析的流场状态量是速度信息，即（u，v），其中u和v分别为直角坐标系下x方向和y方向的速度。具体表示为

其次，基于流场快照，形成包含系统流动特征结构及时空演化信息的矩阵A。如果采样的样本Vn1大到可以完全描述原流场的时空演化特征，可假设两个相邻的流场快照vi和vi＋1可以由线性变化A联系起来，即

同时，假设这种变换关系在Δx足够小时对于整个抽样空间［0，（n－1）Δx］均适用。由于分布间隔相同，该流动序列可由Krylov序数表示，即

DMD理论假设当快照的个数超过某个值后，式（4）的向量为线性相关，即超过某一临界个数后，整体向量空间将保持不变，此时即使再增加更多的快照也不会对其产生影响。达到临界值后，第n个向量vn可由前n－1个向量线性表示，

式中：aT＝［a1a2… an－1］；r为残值向量。

同时，可以得到

式中：en－1∈Rn－1为n－1阶单位向量；Vn2和Vn－11均从CFD数值模拟结果中提取。由于矩阵A是一个反映流场内在动力学机制，且具体形式未知的高维矩阵，所以DMD方法采用A的伴随矩阵S来作为A的低维近似。S的表达式为

接下来的工作就是从利用A的伴随矩阵提取基于数据序列Vn1的动态特征。可以参照文献［22］通过对Vn1的QR分解来解出S的具体形式，其中Q为正交矩阵；R为上三角矩阵。Schmid［22］指出这种解法虽然理论上正确，但实际应用中却是一个无法提取出多于第一阶或前两阶主导模态的病态方法。尤其当快照数据被噪声或其他因素污染时，这种现象更加严重。为了解决上述问题，选择鲁棒性更好的满秩矩阵珘S代替S。

下面简述满秩矩阵珘S的求解过程：

对由流场快照组成的矩阵Vn－11进行奇异值分解，得到

式中：U为Vn－11的左奇异矩阵；Σ为半正定对角矩阵，对角线上的元素是奇异值，Σ＝diag（σ1，σ2，…，σn－1），其中σi按从大到小的顺序进行排列；WT为的右奇异矩阵。代入式（6），两端左乘UT和右乘以WΣ－1得到

这样就得到了满秩矩阵珘S的具体形式。随后采用QR分解求珘S的特征值和特征向量。珘S＝YΛY－1代入式（9）得到AUY＝UYΛ，令＝UY。Y为珘S的特征向量矩阵；为A的特征向量矩阵。也就是说，矩阵A和矩阵珘S的特征值相同，均为Λ＝diag（μ1，μ2，…，μn－1）。这样，通过满秩矩阵珘S就得到了A的特征值和特征模态。

最后，对DMD分析得到的A的特征值进行对数映射，得到空间模式下的特征值为

式中：μ＝μre＋μimi为DMD方法得到的流动特征值；λre为指数放大率或衰减率；λim为空间波数，i为虚数单位（i2＝－1）。

2 基于DMD的翼型转捩预测方法

2．1 DMD／eN方法

本文运用DMD取代线性稳定性分析，并与eN转捩预测方法结合，提出了一种适用于翼型定常与非定常流动的转捩预测新方法。

基于线性稳定性分析的eN方法，由于平行流假设的引入，使得流动的横向速度和流向参数的弱增长被忽略。该方法不仅对层流解的精度要求较高，稳定性方程求解的鲁棒性欠佳，并且不能直接用于非定常流动的转捩预测。而本文采用的DMD方法，直接从实验或者CFD数值模拟结果中提取数据，不对数据做任何假设，克服了线性稳定性分析的以上缺点。文献研究表明，DMD的分析结果等价于全局稳定性分析的结果［22］，可以很好捕捉系统的动力学特征，得到不稳定的主导模态及其对应的特征值。DMD方法的优势在于无须解庞大的全局稳定性矩阵即可获得全局动态特征。

2010年Schmid提出了基于瞬时流场的DMD方法，并且比较了平面Poiseuille流线性小扰动的Orr－Sommerfeld方程的精确特征值与DMD分析所得的特征值，验证了DMD方法的收敛性和有效性［22］。

本文提出如下将动模态分解方法和eN转捩方法结合的过程：

1）将翼型上下表面沿翼型弦线方向等分L段。理论上分成的段数越多得到的转捩点位置越精确，但是需要的流场快照数也越多；而为保证流场快照的精度则要求更大的网格量，从而带来更大的计算量。若是分段过少，则转捩位置精度很难保证。本文作为方法的初步探索，将翼型上、下表面各分为10段。

2）对翼型表面每一段的流场快照数据进行DMD计算，得到每一段表征稳定性的特征值。值得注意的是，在DMD实际应用中，常常要去除流场中的噪声以及不重要的流动结构对DMD计算的干扰。而对流场快照矩阵进行奇异值分解后，得到的奇异值大小代表所对应的流场结构对流场的贡献，奇异值σi越大表示对应的模态在流场中所占比重越大。其中，奇异值过小的模态对流场的贡献很小，有时可能是由数值误差引起的。因此奇异值的大小可以作为预处理的阀值。根据流动特点确定合适的阀值σ，选择σi／σ1≥σ的奇异值对应的模态进行分析，目的是降低数值误差对结果的影响。本文选择σ＝10－8进行分析计算。

3）确定流场演化矩阵A的有效特征值。本文参照文献［15］中通过对每一段内取不同快照进行DMD分析（例如取80个和100个流场快照），选择不稳定特征值（λim，λre）分布重合度最好的特征值作为本段的有效特征值，对应的模态即是本段的特征模态。研究中发现数值噪声对DMD分

5）逐段向后推进求解，找出扰动放大因子超过转捩阀值时对应的段标号l。通过Nl与转捩阀值的比较，线性插值得到阀值对应的转捩点位置xtran。

本文发展的绕翼型定常流动的转捩预测具体过程如图2所示。首先采用固定转捩方法对绕翼型的流动进行数值模拟，在保证较大层流范围的前提下使流场充分收敛；其次，提取边界层内的速度信息，插值形成流场快照；而后，采用DMD／eN方法进行转捩预测；最后，将得到转捩位置回带至RANS求解器，直至得到收敛的解。析的结果影响较大，在这里选取两种快照数重叠性最好的特征值的目的是为了避免数值噪声干扰。由于80快照和100快照的特征值中重叠最好的两个也存在些微小差异（并不是完全重合），故以流场快照数多的100快照的结果为准。

4）利用式（11）对DMD分析得到的空间放大率进行积分，得到从翼型前缘开始到第l段末尾的扰动累计放大因子Nl（下标l为段标号）：对于非定常效应不是十分显著的翼型绕流，本文采用如图3所示的转捩预测过程。首先，进行固定转捩的定常RANS求解，得到一个初步的流场；以定常计算的初始流场为非定常计算0时刻的初值，进行非定常RANS的迭代，直至得到周期性变化的力系数，则认为流场收敛，保存不同物理时刻的流场数值。其次，提取非定常计算中一个周期内不同物理时刻的速度流场数据，分别采用DMD／eN方法进行转捩预测。最后，将不同时刻的转捩位置带回非定常RANS进行计算，直至得到收敛的解。

2．2 DMD／eN方法原理分析

理论分析和证明DMD／eN方法的理论依据，以及与基于线性稳定性分析的eN方法（LST／eN）的联系。

LST／eN方法是在定常层流边界层中引入一个小扰动，通过解线性稳定性方程来确定中性曲线上不同频率的扰动在流向不同站位处特征值（空间波数和放大率）；然后，对每个频率下的放大率沿流向进行积分，得到若干N值增长曲线，并通过与阀值的比较得到转捩点。

而本文提出的DMD／eN方法采用类似的思路，其理论的合理性取决于如下一个结论：DMD分析得到的每段流场演化矩阵A的特征值（对数映射后的实部），是该段“特征扰动”的平均放大率。所谓特征扰动，是指由DMD分析的特征值所对应的扰动。下面对这一结论进行理论证明：

在翼型表面划分的某一段流场内，DMD分析的流场快照矩阵为

式中：珋vi为层流边界层的速度。根据DMD理论，假设流场快照数足够多，包含了所有空间演化信息，则两个相邻快照间的关系可以写为

假设在第i站位处平均速度项中存在扰动δi，沿流向进行演化得到i＋1站位的δi＋1。假设扰动足够小，使得加上扰动后的流场仍然满足关系式（13），则有

结合式（13）和式（14）可得

式（15）表明，第i＋1站位处的扰动可由矩阵A与第i站位处的扰动联系起来。A是由流场的内在动力学机制（主控方程）决定。而A的特征值μ＝e（λre＋iλim）Δx和 特 征 向 量 反 映 了 扰 动 在 空 间 的演化。

参照LST方法，可以构造扰动的表达式为

式中：k为由矩阵A得到的圆频率为ωk的扰动的特征向量，下标k为自定义的不同时间频率标号；λre和λim与式（10）中含义一致，分别为 DMD分析得到的特征值μ对数映射后的放大率和空间波数。

由式（15）和特征值的定义可知，在第i站位处的扰动，到i＋1站位处演化为

照数从1到n），平均的扰动放大率为

这就证明了DMD分析得到的特征值为某频率的扰动在该段上的平均放大率。回顾证明过程，式（13）为DMD理论合理假设，而式（16）为类似于LST理论的合理假设，其余均为严格的数学推导。

在完成了DMD进行稳定性分析的理论推导后，下面将对DMD／eN转捩预测方法的原理做一理论解释。

DMD／eN方法的原理可以概述为：从定常层流解中提取边界层速度信息，分析得到流向每段上“特征扰动”模态和对应的特征值；由于所提取的特征值实部对应了扰动在该段上的放大率，因此对其放大率进行积分可以得到N值增长曲线，并通过与阀值的对比来预测转捩点位置。与LST／eN方法不同的是，DMD是数据驱动的稳定性分析方法，它不需要通过求解线性稳定性方程得到一系列圆频率下的扰动增长曲线。虽然在构造扰动时也考虑了时间频率项，但计算过程中并不需要计算该频率具体是多少，而只关心“特征扰动”的放大率信息。

在运用DMD进行稳定性分析的基础上，本文提出的转捩预测方法实际上类似于eN包络线方法。所计算得到的每段上重叠最好的特征值，一般来讲对应的LST／eN方法中包络线上平均放大率最大的扰动。需要说明的是，每段上的有效特征值对应的并不是同一个时间频率，这与eN包络线法中包络线上对应的有时不是同一时间频率是类似的。

总之，所提出的DMD／eN转捩预测方法，不需要算出不同时间频率下扰动的增长情况，而是采用了类似于eN包络线方法的原理（算例部分将会与基于线性稳定性分析的eN包络线方法作比较）。也就是先计算出每段“特征扰动”的放大情况，进行叠加得到一条类似包含若干扰动的包络线，然后将阀值与包络线上的N值增长做对比，预测出转捩点位置。

3 算 例

3．1 算例1：NLF0416翼型定常流动转捩预测

为 验 证 DMD／eN方 法 的 有 效 性，选 择NLF0416翼型［26］进行数值模拟。计算状态为：马赫数Ma＝0．1，雷诺数Re＝4×106，迎角α＝0°。采用RANS求解器，湍流模型为Spalart－Allmaras模型。图4给出了NLF0416的网格图，网格单元数为640×240，其中翼型上下表面共有512个网格单元，第1层网格距物面高度为2×10－6c。其中，c为翼型弦长。采用课题组自主研发的二维流动求解程序PMNS2D对翼型进行固定转捩数值模拟，上下表面的初始固定转捩点位置设在约60%弦长处（必须保证足够的层流区用于DMD分析）。当流场充分收敛后，提取流场信息，通过插值形成流场快照。图5给出了翼型上表面0．1c～0．2c区间，流场快照取80，σ＝10－8的模态特征值（μre和μim分别为矩阵A的特征值μ的实部和虚部）。位于单位圆之外的特征值是不稳定模态对应的特征值；位于单位圆上的特征值对应的模态是平均流动；位于单位圆之内的特征值是稳定特征值，其对应的模态是稳定的模态。图6给出了分别采用50、80和100快照数分析得到的特征值分布图。上三角、方框与倒三角分别表示流场快照数n＝100，80，50的特征值分布。可以看出3种流场快照数分析得到的特征值呈收敛的趋势。由于横坐标和纵坐标的尺度相差较大，故图中看似重叠最好的点并不是距离最小的点，实线框中的3个为距离最小的不稳定特征值，代表着该段的特征模态。无论采用50快照或80快照标定都得到是同样的有效特征值。这里采用了80快照来选择重叠性最好的100快照的特征值作为有效特征值。

图7 给出了有效特征值的选取示意图，实线方框选中的点是不稳定特征值中重叠性最好的点。根据2．1节的特征值选取标准，这里选择100快照对应的特征值为有效特征值，80快照相当于标定作用。按照2．1节叙述的方法，分别得到翼型上下表面每一段80快照和100快照对应的扰动放大率及N值发展过程（上表面的结果见表1，下表面的结果见表2）。表中x／c为翼型表面的坐标；λre为对应站位的扰动放大率；N为对扰动放大率沿弦向积分得到的N 值。这里只展示了初始固定转捩层流区内（60%弦长范围）的N值增长，此后为湍流区，按照原理不必进行DMD分析。转捩阀值取6，以快照数多的（100快照）N值发展曲线作为转捩位置判断依据，分别将超过转捩阀值的位置及对应的转捩阀值用黑体字表示。从表中右半部分100快照的对应列可看出上表面N值在40%弦长处超过阀值，下表面在50%弦长处超过阀值。同时，给出了线性稳定性分析的结果，转捩阀值N也取为6。翼型上表面和下表面的扰动增长曲线分别如图8和图9所示，图中：xtr＿up和xtr＿low分别为上表面和下表面转捩阀值的位置。

图10给出了NLF0416算例中LST／eN方法与DMD／eN方法的扰动增长曲线对比。黑色粗虚线是DMD／eN方法的N 值增长曲线；其他为LST／eN方法不同特征频率f扰动波的N 值增长曲线。从图中看出，DMD／eN方法的N 值增长曲线很接近LST／eN方法的包络线。虽然个别站位处有些差异，但大体的增长趋势是一致的，转捩点位置比LST／eN方法计算的略微靠前，但误差很小，在合理范围内。这也在一定程度上验证了DMD／eN方法的正确性。

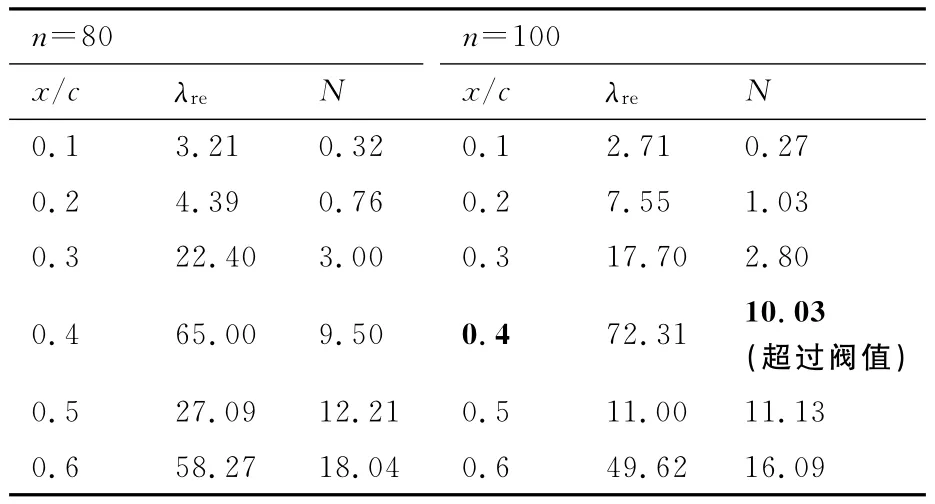
表1 DMD计算的NLF0416翼型上表面N值（Ma＝0．1，Re＝4×106，α＝0°，σ＝10－8，N＝6）Table 1 Nfactor calculated by DMD for upper surface of NLF0416airfoil（Ma＝0．1，Re＝4×106，α＝0°，σ＝10－8，N＝6）

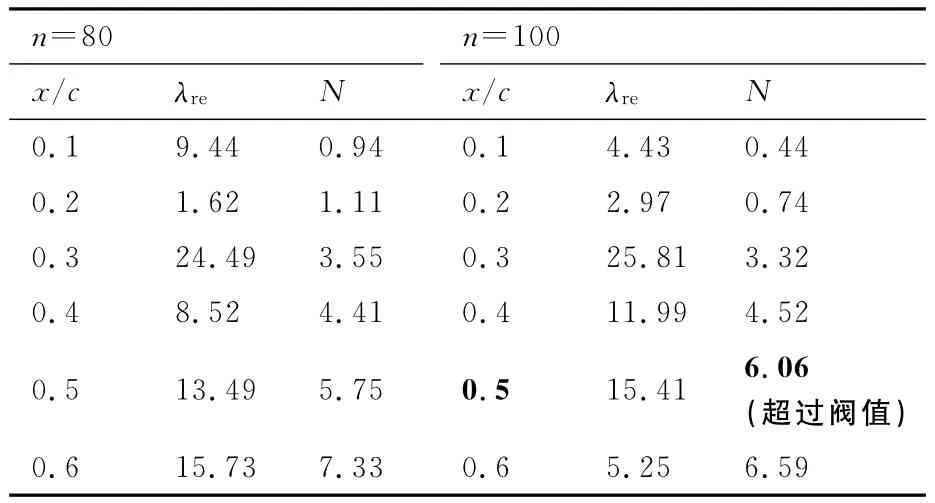
表2 DMD计算的NLF0416翼型下表面N值（Ma＝0．1，Re＝4×106，α＝0°，σ＝10－8，N＝6）Table 2 Nfactor calculated by DMD for lower surface of NLF0416airfoil（Ma＝0．1，Re＝4×106，α＝0°，σ＝10－8，N＝6）

将 DMD／eN方法与 LST／eN方法的转捩点计算结果与实验值进行对比。上表面和下表面的结果及误差分析分别如表3和表4所示。误差计算方法为其中，实验测得的是翼型表面层流区和湍流区位置，转捩点应位于两者之间。由表3和表4可以看出，由100快照得到的上下表面转捩点位置均在实验值对应的层流区处，与线性稳定性分析的结果相近，是合理的结果。将得到的转捩点位置回带至RANS求解器，迭代至流场收敛。得到的阻力系数CD与实验值及全湍流的比较如表5所示，可以看出自由转捩计算所得的阻力系数相比全湍流更加接近实验值。同时将翼型表面的压力分布，与全湍流计算的结果及实验值进行比较，如图11所示。图中：方块为实验测得的压力系数Cp分布；虚线为全湍流计算的结果；实线为DMD分析得到的转捩点带回RANS求解器得到的压力系数分布。可以看出，考虑转捩和全湍流计算的压力系数分布与实验值均吻合良好，但是在上表面转捩位置附近和上表面后缘处，自由转捩的结果与实验值更加吻合。图11（b）给出了压力系数分布的局部放大，可以看出在压力系数分布拐折处自由转捩结果与实验值更接近。

表3 NLF0416翼型上表面转捩点位置计算值与实验比较Table 3 Comparison of predicted transition location with experimental data for upper surface of NLF0416 airfoil

表4 NLF0416翼型下表面转捩点位置计算值与实验比较Table 4 Comparison of predicted transition location with experimental data for lower surface of NLF 0416 airfoil

表5 NLF0416翼型计算阻力系数与实验值的比较Table 5 Comparison of calculated drag coefficient with experimental value for NLF0416airfoil

因湍流黏性系数远大于层流黏性系数，故层流与湍流两种流态下物面的摩擦阻力差异很大。在图12中给出了NLF0416翼型全湍流和自由转捩状态下的物面摩擦力系数Cf分布。其中虚线是全湍流摩阻系数，点画线是LST／eN方法得到的结果，实线是DMD／eN方法得出的结果。由图可看出，LST／eN和 DMD／eN两种方法得到的摩阻系数分布吻合良好。翼型上下表面的摩阻系数分别在各自转捩点附近有一个突增，对应位置在0．35和0．50左右。转捩点位置之前是层流区，全湍流的模拟结果与自由转捩差异很大，Cf远大于自由转捩的结果，而转捩点之后进入湍流，Cf的值开始逐步接近。

3．2 算例2：S809翼型定常流动转捩预测

为了进一步验证本文方法的正确性，选择了转捩点位置实验值丰富的风力机翼型S809［27］进行DMD分析与转捩预测。计算状态：Ma＝0．1、Re＝2×106、α＝0°。转捩后的湍流区域采用Spalart－Allmaras湍流模型。S809翼型计算网格如图13所示，计算网格量为640×256，第一层网格高度为2×10－6c。根据以往的经验，在利用eN方法进行风力机翼型绕流的转捩预测时，阀值N取为6较为合适。在进行DMD分析时为了排除数值噪声的影响，σ取10－8。分别取50和100快照对翼型每段进行DMD分析，得到的上表面和下表面扰动放大率及N值的发展过程分别如表6和表7所示。可以看出100个流场快照对应的上表面和下表面超过转捩阀值的点，分别在60%弦长和50%弦长处。对N值插值后的上、下表面的转捩点位置与实验值［27］的比较如表8所示。可以看出，本文得到的上、下表面转捩点位置均与实验值吻合良好。

表6 DMD计算的S809翼型上表面N值（Ma＝0．1，Re＝2×106，α＝0°，σ＝10－8，N＝6）Table 6 Nfactor calculated by DMD for upper surface of S809airfoil（Ma＝0．1，Re＝2×106，α＝0°，σ＝10－8，N＝6）

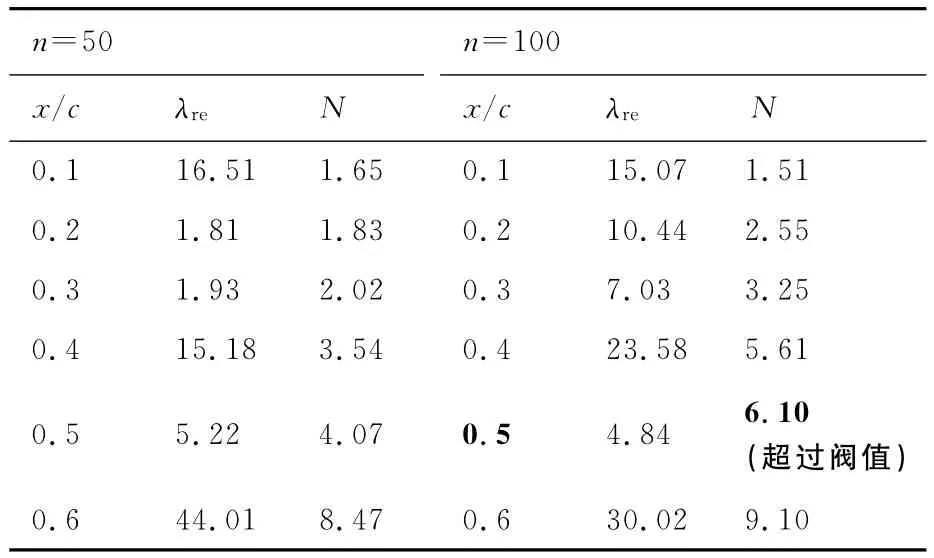
表7 DMD计算的S809翼型下表面N值（Ma＝0．1，Re＝2×106，α＝0°，σ＝10－8，N＝6）Table 7 Nfactor calculated by DMD for lower surface of S809airfoil（Ma＝0．1，Re＝2×106，α＝0°，σ＝10－8，N＝6）

表8 S809翼型上、下表面转捩点位置计算值与实验值比较Table 8 Comparison of predicted transition location with experimental data for upper and lower surface of S809airfoil

图14和图15分别为自由转捩和全湍流计算得到的S809翼型的整体及分离泡附近的局部放大流线图。可以看出，自由转捩计算很好地模拟出了分离泡的存在，而全湍流则没能模拟出流动中的分离泡。图16是全湍流及考虑转捩计算的压力系数分布与实验值的比较，图中方块表示实验测得的压力系数分布，点画线是全湍流计算的结果，实线是流场快照为100时得到的转捩位置回带至RANS求解器的结果。可以看出，自由转捩的计算的压力系数分布更加接近实验值，尤其在分离泡处的模拟结果明显优于全湍流。其中，翼型上表面半弦长处有明显的分离泡，下表面在半弦长靠前的位置也存在小的分离泡，这与文献［27］中实验结果的描述也完全一致。总之，通过对NLF0416及S809翼型的转捩点位置的计算及与实验值的比较，验证了DMD／eN方法用于翼型定常流动转捩预测的可行性和正确性，同时也表明DMD／eN方法能够处理含层流分离泡的转捩预测问题。

3．3 SD7003翼型非定常流动转捩预测算例

本文以低雷诺数下SD7003翼型做俯仰运动的非定常流动为例，进行了基于DMD的非定常转捩预测。为了保证边界层信息的精度，选择网格量为640×256，第1层网格高度为1×10－6c，网格示意图如图17所示。计算状态：Ma＝0．05，Re＝6×104，运动规律：α＝5．5°±3°sin（ωt），其中减缩频率为k＝ωc／2U∞＝0．52。

首先进行了定常固定转捩计算，为非定常流动提供初始流场。然后进入非定常固定转捩计算，初始固定转捩点位置上、下表面均取为0．6c。其中每个运动周期划分为300个物理时间步，每个物理时间步内子迭代20步，共计算6个周期。得到具有周期性变化的力系数和流场，则认为流场收敛。

对于这种频率较小，非定常效应不是特别明显的翼型俯仰运动算例，转捩预测过程中采用准定常的处理方法，与文献［15］中采用的处理方法一致。

在非定常流场充分收敛的情况下，分别提取（k／8）T（k＝0，1，2，…，8）时刻的流场数据，进行坐标转化、流场插值和DMD计算，提取有效特征值并结合eN方法得到各自时刻的转捩点位置，进而得到一个运动周期内的转捩曲线，如图18所示。这里选取有效特征值的方法与定常算例所采用方法相同，是采用50和100快照重叠性最好的作为有效特征值。

图18中圆圈是实验测得的非定常转捩点位置，虚线是文献［15］利用线性稳定性分析程序结合eN方法得到的转捩点位置。点画线是文献［13］，即Radespiel等通过在非定常RANS方程求解器中耦合基于线性稳定性理论拓展的eN转捩预测方法，对该算例的模拟结果。其在湍流模型的选择，稳定性分析方法和转捩预测方法上与本文有所不同。实线是本文方法所得的非定常流动1个周期内的转捩点位置。可以看出，本文得到的结果在总体趋势上和文献［13］是一致的，并且在大部分时刻都与其结果相近，但在t／T＝2／8，3／8时刻的转捩点位置与实验值及文献值［13］相比稍微靠后。因为文献［13］采用的是拓展的eN方法，考虑到了流动的完全非定常效应，而本文与文献［15］采用的都是标准的eN方法，用准定常的方式处理，故在一定程度上降低了预测精度，这也是在个别时刻转捩点位置没有文献［13］与实验值吻合好的原因。

将本文得到的转捩点位置回带至流场求解程序中，迭代求解至流场收敛。得到典型时刻的压力系数分布及流场的压力云图和流线图，如图19所示。可以看出翼型在初始位置（α＝5．5°）有一个小的层流分离泡，随着翼型的抬头运动，分离泡逐渐变大。当翼型在达到最大迎角（α＝8．5°）后做下俯运动，分离泡逐渐变长并向翼型后缘移动。达到最低位置（α＝2．5°）后，翼型又进行抬头运动回到初始位置，分离泡也逐步脱落，最终回到初始状态。从图中能较为清楚地看出1个周期内翼型做俯仰运动的分离泡的运动发展过程，以及对应的压力系数分布的变化情况。通过与文献［13］及文献［15］的对比可知，本文的方法也能较好地模拟出翼型俯仰运动中的非定常特性，以及转捩位置和分离泡的发展变化。其对于研究和分析低雷诺数下非定常流动特性也具有一定价值。更加精确的非定常转捩预测需要在后续工作中考虑完全非定常效应对转捩预测的影响。

4 结 论

1）DMD方法能直接从流场数据中分析翼型边界层内的扰动放大，无需求解稳定性方程。多个验证算例表明该方法预测的转捩位置均与实验值吻合良好，且与线性稳定性分析的结果相当，说明本文提出的方法是正确的。

2）在进行定常流动转捩预测时，通过选取不同流场快照数（例如快照数为50、80和100），对DMD分析得到的特征值进行比较，选取重叠度最好的不稳定特征值作为有效特征值，是一种合理的有效特征值选取方法。

3）对DMD分析得到的翼型表面各段的扰动放大N因子进行线性插值，可提高转捩位置预测的精度。

4）对于非定常效应不显著的翼型绕流，采用本文发展的转捩预测方法，对每个时刻进行空间DMD分析和转捩判定，仍然可以得到较合理的结果。

本文工作展望如下：针对三维流动机翼TS波诱导的转捩，本文方法应该是能够直接推广应用的。因为DMD在计算中不依赖边界条件和控制方程，且能较灵活地应用于复杂流动和子域分析。初步设想为，将机翼沿展向划分为若干截面，在每个截面处应用类似二维的转捩预测方法得到对应展向位置处的转捩点，通过插值得到机翼表面的转捩线，类似于eN方法对机翼转捩预测的处理［28］。若进一步考虑CF波的情况，由于转捩机理更为复杂，还有待于进一步深入研究。

致 谢

本文所提出的转捩预测新方法，是在与西班牙马德里理工大学（UPM）的Esteban Ferrer博士的合作过程中得到启发，主要由我们课题组教师和研究生历时3年完成的。在此感谢Esteban Ferrer博士的大力支持，感谢他提供了DMD分析程序，并给予我们很多有益的建议。

［1］ 符松，王亮．湍流转捩模式研究进展［J］．力学进展，2007，37（3）：409－416．FU S，WANG L．Progress in turbulence／transition modelling［J］．Advances in Mechanics，2007，37（3）：409－416（in Chinese）．

［2］ 周恒．关于转捩和湍流的研究［C］／2003空气动力学前沿研究论文集．北京：中国空气动力学会，2003：87－93．ZHOU H．Studies on transition and turbulence［C］／2003 Advanced Research Papers on Aerodynamics．Beijing：Aerodynamic Society of China，2003：87－93（in Chinese）．

［3］ FASEL H F，MEITZ H L，BACHAN C R．DNS and LES for investigating transition and transition control：AIAA－1997－1820［R］．Reston：AIAA，1997．

［4］ SCHLATTER S．Assessment of direct numerical simulation data of turbulent boundary layers［J］．Journal of Fluid Mechanics，2010，659：116－126．

［5］ BRAZELL M J，KIRBY A，STOELLINGER M，et al．Using LES in a Discontinuous Galerkin method with constant and dynamic SGS models：AIAA－2015－0060［R］．Reston：AIAA，2015．

［6］ 陈奕，高正红．Gamma－Theta转捩模型在绕翼型流动问题中 的 应 用 ［J］．空 气 动 力学学报，2009，27（4）：411－419．CHEN Y，GAO Z H．Application of Gamma－Theta transition model to flows around airfoils［J］．Acta Aerodynamic Sinica，2009，27（4）：411－419（in Chinese）．

［7］ MENTER F R，LANGTRY R B，LIKKI S R，et al．A correlation－based transition model using local variables—Part I：model formulation［J］．Journal of Turbomachinery，2006，128（3）：413－422．

［8］ GRABE C，KRUMBEIN A．Extension of theγ－Reθtmodel for prediction of crossflow transition：AIAA－2014－1269［R］．Reston：AIAA，2014．

［9］ 符松，王亮．基于雷诺平均方法的高超音速边界层转捩模拟［J］．中国科学：G辑，2009，39（4）：617－626．FU S，WANG L．Modelling flow transition in a hypersonic boundary layer with Reynolds－averaged Navier－Stokes approach［J］．Science in China：Series G，2009，39（4）：617－626（in Chinese）．

［10］ STOCK H W，HAASE W．Navier－Stokes airfoil computations with eNtransition prediction including transitional flow regions［J］．Journal of Aircraft，2000，38（11）：2059－2066．

［11］ 张坤，宋文萍．NS方程计算中耦合转捩自动判断的阻力精确计算方法初探［J］．空气动力学学报，2009，27（4）：400－404．ZHANG K，SONG W P．Accurate drag calculation by coupling automatic prediction of transition point to the Navier－Stokes method［J］．Acta Aerodynamic Sinica，2009，27（4）：400－404（in Chinese）．

［12］ KRUMBEIN A，KRIMMELBEIN N，SEYFERT C．Automatic transition prediction in unsteady airfoil flows using an unstructured CFD code：AIAA－2011－3365［R］．Reston：AIAA，2011．

［13］ RADESPIEL R，WINDTE J，SCHOLZ U．Numerical and experimental flow analysis of moving airfoils with laminar separation bubbles［J］．AIAA Journal，2007，45（6）：1346－1356．

［14］ WINDTE J，RADESPIEL R．Propulsive efficiency of a moving airfoil at transitional low Reynolds numbers［J］．AIAA Journal，2008，46（9）：2165－2177．

［15］ 刘方良．低雷诺数翼型流动转捩判断与优化设计方法［D］．西安：西北工业大学，2014：33－67．LIU F L．Transition prediction and optimization design method for low－Reynolds－number airfoil［D］．Xi’an：Northwestern Polytechnical University，2014：33－67 （in Chinese）．

［16］ HERBERT T．Parabolized stability equations［J］．Annual Review of Fluid Mechanics，1997，291（1）：245－283．

［17］ BERTOLOTTI F P，HERBERT T．Analysis of the linear stability of compressible boundary layers using the PSE［J］．Theoretical and Computational Fluid Dynamics，1991，3（2）：117－124．

［18］ NOACK B R，MORZYNSKI M，TADMOR G．Reducedorder modelling for flow control［M］．Udine：CISM，2011：77－110．

［19］ CHATTERJEE A．An introduction to the proper orthogonal decomposition［J］．Computational Science，2000，78（7）：808－807．

［20］ SIROVICH L．Turbulence and the dynamics of coherent structures［J］．Quarterly of Applied Mathematics，1987，45（3）：561－590．

［21］ BERKOOZ G，HOLMES P，LUMLEY J L．The proper orthogonal decomposition in the analysis of turbulent flows［J］．Annual Review of Fluid Mechanics，1993，25（1）：539－575．

［22］ SCHMID P J．Dynamic mode decomposition of numerical and experimental data［J］．Journal of Fluid Mechanics，2010，656：5－28．

［23］ ROWLEY C，MEZIC I，BAGHERI S，et al．Spectral analysis of nonlinear flows［J］．Journal of Fluid Mechanics，2009，641：115－127．

［24］ SCHMID P J，LI L，JUNIPER M，et al．Applications of the dynamic mode decomposition［J］．Theoretical and Computational Fluid Dynamics，2011，25（1－4）：249－259．

［25］ SCHMID P J．Application of the dynamic mode decomposition to experimental data［J］．Experiments in Fluids，2011，50（4）：1123－1130．

［26］ SOMERS D M．Design and experimental results for a natural－laminar－flow airfoil for general aviation applications：NASA－TP－1861［R］．Washington，D．C．：NASA，1981．

［27］ SOMERS D M．Design and experimental results for the S809airfoil：NREL／SR－440－6918［R］．Colorado：NREL，1997．

［28］ 张坤．基于NS方程的机翼边界层转捩判断及应用研究［D］．西安：西北工业大学，2011：97－157．ZHANG K．Automatic transition prediction and application to 3Dswept wings［D］．Xi’an：Northwestern Polytechnical University，2011：97－157（in Chinese）．

A novel method for automatic transition prediction of flows over airfoils based on dynamic mode decomposition

HAN Zhonghua＊，WANG Shaonan，HAN Li，LIU Fangliang，XU Jianhua，SONG Wenping
National Key Laboratory of Science and Technology on Aerodynamic Design and Research，School of Aeronautics，Northwestern Polytechnical University，Xi’an 710072，China

Transition prediction is crucial for the simulation of steady and unsteady flows，since it can improve the accuracy of predicting the aerodynamic forces as well as capturing the flow phenomena．By combining dynamic mode decomposition（DMD）and eNmethod，a novel transition prediction method for flows over airfoils is proposed．Compared with conventional linear stability－analysis－based eNmethod，DMD requires neither the solution of boundary layer and linear stability equations，nor the assumption of parallel flows，and has better applicability in theory and is more algorithmically robust．Transition prediction of steady flows around NLF0416and S809airfoils and unsteady flow around SD7003airfoil are carried out．The predicted transition locations are in reasonably good agreement with the experimental data and the results of eNmethod based on linear stability analysis．It is shown that the proposed DMD／eNmethod is feasible for transition prediction for steady and unsteady flows over airfoils，including the flows with laminar separation bubbles．

transition prediction；dynamic mode decomposition；eNmethod；airfoil；computational fluid dynamics

2016－01－11；Revised：2016－01－31；Accepted：2016－07－21；Published online：2016－08－08 08：41

URL：www．cnki．net／kcms／detail／11．1929．V．20160808．0841．002．html

s：National Natural Science Foundation of China（11302177）；Civil Aircraft Project（MJ－2015－F－016）

V211．3

A

1000－6893（2017）01－120034－17

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

10．7527／S1000－6893．2016．0225

2016－01－11；退修日期：2016－01－31；录用日期：2016－07－21；网络出版时间：2016－08－08 08：41

www．cnki．net／kcms／detail／11．1929．V．20160808．0841．002．html

国家自然科学基金 （11302177）；民机专项 （MJ－2015－F－016）

＊通讯作者 ．E－mail：hanzh＠nwpu．edu．cn

韩忠华，王绍楠，韩莉，等．一种基于动模态分解的翼型流动转捩预测新方法［J］．航空学报，2017，38（1）：120034．HAN Z H，WANG S N，HAN L，et al．A novel method for automatic transition prediction of flows over airfoils based on dynamic mode decomposition［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：120034．

（责任编辑：鲍亚平）

＊Corresponding author．E－mail：hanzh＠nwpu．edu．cn