思前想后定目标，必要讲授求高效

陈爱军

[摘 要] 为了后续学习“式”的运算更加高效，在整式加减起始课教学时需要给出一些与整式相关的新概念，所以怎样让学生准确理解这些概念，并通过适量的练习深刻理解这些概念，值得教师在备课时认真构思.

[关键词] 整式；单项式；多项式；教学立意；符号意识；必要讲授

笔者最近有机会执教“整式（第1课时）”的教学研究课，对该课时的教学有了较长时间的思考，本文梳理该课的教学流程，并跟进教学立意的解读，提供研讨.

“整式（第1课时）”教学流程

1. 教学环节一：创设情境，引入新课

问题1 如果要表示一个任意数的相反数，你能用符号简明表达吗？（n的相反数为-n）

问题2 小学里我们积累了哪些图形的面积、周长和体积公式？你能用符号简要表达吗？

教学实施 先安排学生在小组内交流、汇总，再全班交流展示，教者预设了以下一些常见的面积、周长、体积公式，在学生说出相应的公式时，可以结合PPT出示.

（2）半径为r的圆的周长为2πr；

（3）边长为a的正方形的面积是a2，周长是4a；

（4）长为a、宽为b的长方形的面积为ab，周长为2a+2b；

……

问题3 用含有字母的式子表示以下数量关系：

（1）每包书有21册，x包书有______册；

（2）某产品前年的产量是a件，去年的产量是前年产量的b倍，用式子表示去年的产量为______件；

（3）一条河的水流速度是5 km/h，船在静水中的速度是v km/h，用式子表示船在这条河中顺水行驶的速度为______km/h，逆水行驶的速度为______km/h；

（4）如图1（单位：cm），用式子表示三角尺的面积为______cm2.

教学实施 先安排学生独立练习，再分组汇报所填写的代数式，并板书在黑板上留作稍后的描述性定义使用.

2. 教学环节二：给出定义，建构理解

教学过渡：上面的问题情境涉及的部分代数式如下.

教学实施 让学生结合问题情境，观察所写式子，从式子所包含运算的角度归纳其特点，给出单项式、多项式的名称，并追问学生：同学们，上面这些式子中哪些属于单项式，哪些属于多项式？

在学生归类正确的基础上，给出单项式与多项式的定义：由数字或字母的乘积组成的式子是单项式，单独的一个数或一个字母也是单项式；几个单项式的和叫做多项式. 单项式与多项式统称为整式.

3. 教学环节三：跟进定义，丰富概念

教师讲授 由于后面要学习整式的运算，所以还需要对单项式中的一些数字因数与字母的指数给出一些新的名称，定义一些概念，比如单项式的系数、次数：

单项式中的数字因数叫做这个单项式的系数（结合黑板上的一些单项式举例讲解）；单项式中所有字母的指数的和叫做这个单项式的次数（结合黑板上的一些单项式举例讲解）.

给出多项式的项、常数项、次数的定义：在多项式中，每个单项式叫做多项式的项（结合黑板上的一些多项式举例讲解）；不含字母的项叫做常数项（结合黑板上的一些多项式举例讲解）；把黑板上举例的一些多项式中的次数最高的项用不同颜色的粉笔圈点或标注出来，指出多项式里次数最高的那一项的次数，叫做这个多项式的次数.

4. 教学环节四：跟进练习，理解概念

给出一组练习题，列式填空，要求根据所列出来的代数式先判断其是单项式还是多项式，如果是单项式，则指出它的系数与次数；如果是多项式，请写出它的项与次数. 限于篇幅，这里不列出这组习题.

5. 教学环节五：课堂小结，串珠成线

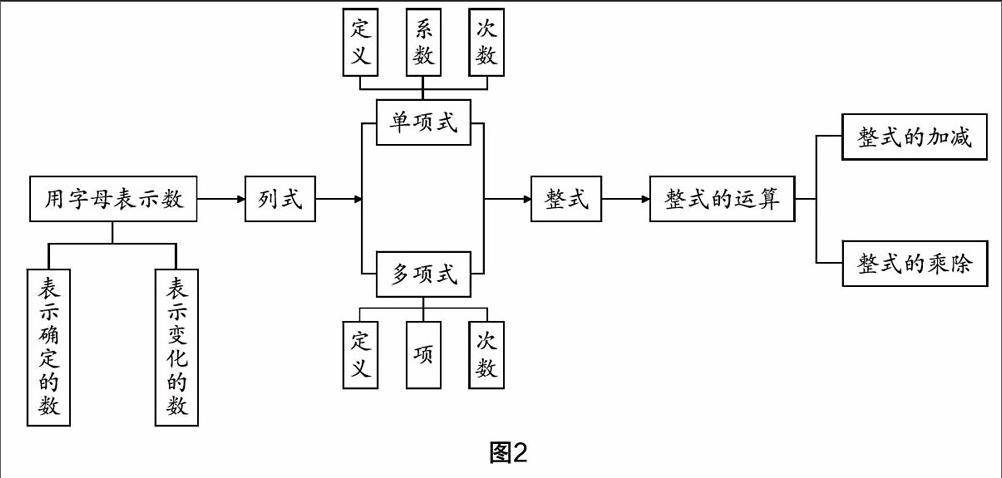
师生合作，把本课内容构思、整理成如图2所示的知识结构图.

教学立意的进一步阐释

1. 第一，“思前想后”，精准定位课时教学目标

有理数之后是整式加减，这是初中数学“数与代数”领域的第二部分内容，其研究内容是对之前所学有理数的加减的“一般化”，又是后续学习方程、不等式、分式、因式分解、函数、二次根式等相关运算的基础. 由于整式的加减是从“式”的角度研究运算，学生的思维有个适应的过程，但从数到式，是初中数学运算的重点与难点. 就“整式加减”整章来说，“用字母表示数”是全章的重点和难点，用字母表示数对学生来说是认识的一大障碍，尤其是字母可以表示包含负数的任何数，这对学生来说需要有个适应过程. 小学时碰到过一些简单的方程，也接触过用字母表示未知数，但是小学阶段仍然是把字母看成一个数，并没有体现出变量的意识，因此，进入初中之后，在教学中要通过大量的问题情境使学生逐步理解字母可以表示“变量”，为后续学习方程、函数服务.

另外，列式的技能也是“整式加减”一章学习时应重点训练的内容，列式能力是文字应用题的基础，也为后续初二、初三學习列方程（组）、不等式（组）、函数关系式解决有关实际问题服务.

在上面“思前想后”的基础之上我们认为，“整式加减（第1课时）”的教学目标可以拟定如下：理解并掌握整式的有关概念，能够对一些整式进行分析；能从具体情境中抽象出数量关系和变化规律，使学生经历对具体问题的探索过程，培养符号意识；通过丰富有趣的现实情境，使学生经历从具体问题中抽象出数量关系的过程；在解决问题中了解数学的价值，增强学生“用数学”的信心. 教学重点是单项式的系数、次数，多项式的项数、次数等概念，难点是对上述新概念的深刻理解与灵活运用.

2. 第二，“符号意识”，引入字母简化数量关系

初中数学在相当长时间都分成两个学科（代数和几何），其中代数，顾名思义就是以字母代替数，用字母代替数，体现了从一般到特殊的数学思想，同时用字母表示出很多数学数量关系，往往使数学关系得以简明化、精确化，可以说符号化表达是数学在新的发展阶段的一个重要学科特点. 而且这种符号系统是数学学科的共通性，即不管是哪个国家、民族、肤色的人，在数学关系的探究与发现时，运用恰当的、统一的符号来表征，都已得到共识，也发展成独具特色的数学符号语言系统. 数学的符号表达还具有简明表示数量关系的学科特点，想来也是符合数学上求简的追求. 我们认为，进入初中学习阶段，我们一方面要加强运算能力的培养，另一方面，要让学生逐步适应用字母表示数的符号表示方法，感悟数学符号语言的简洁与“一般化”（与特殊数值相比的一般化，还有很多例子，比如中国古代数学中记录的“勾三股四弦五”，比如费马大定理的故事中体现的从特殊到一般的深入思考，这些在以后学习时都可提及并让学生进行类比体会）.

3. 第三，“必要讲授”，举例讲解新定义、新概念

经过不少专家、学者对“课改”中很多激进的表达的反思之后，我们对教师在课堂上的必要讲授有了更客观的认识，即教师在课堂上的必要讲授是需要的，具体要由教学内容来决定选择何种方式教学. 像整式的概念（单项式、多项式，单项式的系数与次数，多项式的项、次数等），数学上的一些定义、约定、概念，也就无须安排所谓学生“假探究、假归纳、假互动”了，在前面问题情境导出一些代数式之后，就由教师直接讲授这些描述性的概念，并针对黑板上已留下来的一些案例，进行圈点、标注式的讲授，让学生听懂、理解、内化新概念，这就是比较务实、高效的教学方式. 这里值得强调的是，数学上有很多概念是描述性的概念，在目前的学段教学要求中，我们不需要（有时也很难）对有些概念进行严谨的定义，只好结合一些例子，概括出新概念. 这方面的概念是很多的，后面要学习的一元一次方程的定义、不等式的定义、分式的定义等，都可看成是描述性概念.

4. 第四，“重视练习”，精心编拟习题层层递进

课时作业需要围绕课例开展作业设计. 作业的目的是评价学生对新知识、新概念的理解. 《义务教育数学课程标准》（2011版）关于“评价建议”有如下表述：“评价的主要目的是全面了解学生数学学习的过程和结果，激励学生学习和改进教师教学.”“评价不仅要关注学生的学习结果，更要关注学生在学习过程中的发展和变化.”所以在上面的课例中，评价环节中的作业侧重的是巩固新课，同时又注意尽可能促进学生的可能发展. 具体来说，所编拟的习题主要是列式以及单项式、多项式的概念；另外，布置作业或跟进练习要分层设计，可以分成必做题和选做题.endprint