倾转旋翼机旋翼/机翼气动干扰理论与试验

张铮， 陈仁良

南京航空航天大学 直升机旋翼动力学国家级重点实验室， 南京 210016

倾转旋翼机旋翼/机翼气动干扰理论与试验

张铮， 陈仁良*

南京航空航天大学 直升机旋翼动力学国家级重点实验室， 南京 210016

采用参数化建模方法，建立了适用于飞行力学分析的倾转旋翼机旋翼/机翼气动干扰模型，提出一套简单而准确的干扰区计算方法，得出了干扰区边界的解析表达式，并根据解析式数值积分得到了干扰区的面积，据此给出了过渡过程中旋翼/机翼气动干扰的速度边界。针对上述模型和方法，进行了倾转旋翼不同旋翼总距、前飞速度以及短舱倾角下的旋翼/机翼气动干扰风洞试验，并通过理论计算结果与风洞试验结果的对比验证建模方法的正确性。

倾转旋翼机； 气动干扰； 干扰边界； 解析表达式； 风洞试验

倾转旋翼机是一种结合了直升机和固定翼飞行器优势的飞行器。既可以悬停飞行又可以高速巡航。但同时也大大增加了飞行器的复杂性，其中之一就是旋翼与机翼之间的气动干扰。倾转旋翼机旋翼和机翼之间的气动干扰对机翼载荷影响较大。在悬停或小速度平飞状态下，旋翼尾迹几乎垂直冲击机翼表面，机翼表面迎角接近90°，使机翼产生了很大的向下载荷[1-4]，其量值可达到旋翼拉力的10%～15%[1,4]，这严重限制了倾转旋翼飞行器的起飞重量及商用载荷。在过渡模式下，发动机短舱向前倾转，旋翼尾流仍然可以到达机翼表面，产生向下的诱导速度，使其产生向下的气动力[4]。因此旋翼/机翼气动干扰不仅会影响倾转旋翼飞行器的悬停性能，还会对过渡模式飞行特性产生重要影响。忽略旋翼/机翼气动干扰会影响整个倾转旋翼飞行器飞行力学模型的准确性[5-8]。

倾转旋翼飞行器旋翼/机翼气动干扰的研究方法主要分为2类。第1类是CFD方法。CFD方法可以捕捉流场细节，给出物面压力分布，准确地计算旋翼或机翼气动力。但CFD方法需要大量的计算网格，计算效率较低，难以适应飞行力学分析的需要。第2类方法将机翼表面分为浸入旋翼尾流的干扰区和旋翼尾流之外的自由流区两部分,分别计算这两部分的面积以及气动力，然后累加得到整个机翼在旋翼干扰下的载荷[6,9-20]。这一方法计算效率高，较好地适应了飞行力学计算需要。但干扰区面积的计算需要利用经验公式[5-7,9-10,20]，公式中的经验系数因机型而异，例如， XV-15倾转旋翼机假设发动机短舱倾转超过30° 或飞行速度大于30 m/s时不考虑旋翼/机翼气动干扰[9-10,13]，当机型变化时，上述假设是否合适值得探讨，这降低了方法的通用性。

为解决这一问题，本文提出了一种新方法来计算旋翼尾迹在机翼表面形成的干扰区。该方法可以以解析表达式的形式给出干扰区边界，包括确定干扰区面积、展向以及弦向位置。算法中不包含干扰区面积的任何经验系数，可以通用于不同机型。而且不受短舱倾转角和飞行速度的限制，可以分析整个过渡过程内旋翼/机翼气动干扰，提高了方法的通用性。用风洞试验数据验证上述方法的正确性，在此基础上确定了前飞状态下干扰区的边界。

1 计算方法

1.1 计算坐标系说明

本文共涉及2个右手坐标系，机体坐标系OBXBYBZB和桨毂坐标系OsXsYsZs。如图1所示，机体坐标系原点OB位于全机质心C处，X轴在全机纵向对称面内，指向机头，Y轴垂直于纵向对称面，指向右侧，Z轴在纵向对称面内，其方向按右手定则确定。桨毂坐标系原点OHubcenter位于桨毂中心H，其Xs轴从方位角0° 指向180°，Ys轴从右旋旋翼的270° 指向90°，Zs轴垂直于桨盘平面，与发动机短舱平行，其方向同样由右手定则确定。桨毂坐标系到机体坐标系之间的坐标转换矩阵TBs为

(1)

式中：βM为发动机短舱倾转角，本文中规定以βM=0° 代表直升机模式，βM=90° 代表固定翼模式。

1.2 基本假设

由于机翼和短舱的存在，倾转旋翼机旋翼尾迹相比于孤立旋翼要复杂得多。此外，由于旋翼尾迹只能影响部分机翼，机翼表面各点的来流速度各不相同。这使得机翼载荷的计算难度大大增加。为了简化问题，本文提出假设如下[6，9-15]：

1) 将旋翼等效为桨盘平面，其半径为R，旋翼尾迹半径为Rw,本文取Rw=0.7R[21]。

2) 旋翼尾流中旋翼诱导速度大小恒定为vi。

3) 将机翼分为受到旋翼尾迹影响的干扰区和处于尾迹区之外的自由流区两部分[9,13]，机翼气动力等于干扰区和自由流区气动力之和。

根据以上假设，若倾转旋翼机短舱角为βM，以速度V飞行，则机翼自由流区来流速度Vf(即图1中的Vf)为

Vf=0-V

(2)

而干扰区来流速度Vt则为

(3)

基于以上假设，旋翼尾流在空间中的几何形状是一个斜圆柱体，该圆柱体轴线即沿矢量Vt方向，如图1中Vt所示。而机翼则为二维平面。机翼浸入旋翼尾流区的面积实际上相当于机翼截斜圆柱体的截面积。这一截面形状较为复杂，在一些干扰区计算的经验公式中将其近似为圆来处理。本文根据空间解析几何原理，建立桨盘平面与机翼平面之间的映射关系，将桨盘平面的点映射到机翼平面，从而得到干扰区边界的参数方程。然后再通过数值积分，得到干扰区的面积和形心。

1.3 干扰区边界的参数方程

在机体坐标系下，发动机短舱支点P坐标为(xPyPzP)，长度为Ln。机翼所在平面方程为z=zx。

旋翼桨盘平面上尾迹边界的任一点e可以标记为(Rw，ψ)，ψ为方位角。该点相对于桨毂中心H的位置矢量rHe在桨毂不旋转坐标系下可以表示为

(4)

转换到机体轴系下，得

(5)

(6)

因此，尾迹边界点e相对于短舱支点的位置矢量在机体轴系下的坐标阵为

(7)

从而，该点在机体轴系下的坐标为

(8)

点e处的尾流到达机翼所在平面的时间Δt为

(9)

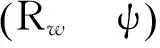
x=-RwcosβMcosψ+LnsinβM+xP+VxΔt

(10)

y=Rwsinψ+yP+VyΔt

(11)

代入式(9)，得干扰区边界参数方程如式(12)、式(13)所示。

x=F(ψ)=

(12)

y=G(ψ)=

(13)

1.4 干扰区位置和面积的计算流程

根据1.3节所得到的参数方程，在某一短舱角和飞行速度下，可以得到干扰区的面积形心坐标。采用数值方法计算干扰区面积和形心。如图2 所示，假设机翼前后缘纵坐标分别为xlead和xtail，沿弦向将机翼划分成N段，对于其中横坐标为x的任意一段，根据参数方程可以确定其最大和最小的纵坐标为y2和y1，此坐标值不应超过机翼展向边界ymax和ymin。则该微段浸入干扰区的面积为dS=dx(y2-y1)，其中dx为微段弦向长度。然后累加即可得到机翼表面干扰区的面积。具体计算流程如图3所示。

干扰区位置，即干扰区形心的计算流程与面积相同，可用式(14)说明：

(14)

式中：rC和rdS分别为干扰区和微元的形心坐标。

1.5 旋翼/机翼干扰边界

(15)

式中：下标f代表自由流区，I代表干扰区。

在没有气动干扰的条件下，机翼迎角α应等于机翼安装角α0和飞行器俯仰角θ之和，即

α=θ+α0

(16)

则由旋翼/机翼气动干扰引起的机翼平均迎角增量为

(17)

假设模型倾转旋翼飞行器总重为G，假定气动干扰引起的机翼载荷不超过全机总重的εG时不考虑旋翼/机翼气动干扰，ε是一个小量，则相应的平均迎角增量为

(18)

式中：α∞为机翼升力线斜率；ρ为来流密度；v为前飞速度。

整理可得

(19)

2 旋翼/机翼气动力计算

为计算不同状态下旋翼/机翼气动力，并以此分析旋翼/机翼气动干扰，本文采用上述干扰计算方法建立了双旋翼机翼系统的数学模型。

2.1 旋翼模型

本文建立了旋翼的单片桨叶模型。采用叶素理论计算旋翼各片桨叶上的气动力并累加，最终获得整副旋翼上的气动力。同时采用动态入流方法[13]计算由旋翼产生的轴向诱导速度。

2.2 机翼模型

机翼气动力系数C与迎角α、侧滑角β、马赫数Ma、襟副翼偏转量δa等多个因素相关，可以简写成如下的函数形式

(20)

利用机翼的风洞试验数据，采用插值的方法可以获得不同状态下机翼的气动力系数。近似认为，机翼气动力由干扰区气动力与自由流区气动力简单叠加而成，即F=Ff+Fi，因此，在分别计算出左右旋翼干扰区面积SL和SR后，由式(21)计算出机翼气动力，其中下标R、L和f分别代表右旋翼、左旋翼干扰区和自由流区，qF为动压。

(21)

3 计算结果与验证

3.1 升力与阻力

为了验证新方法的正确性，本文以小型无人倾转旋翼机为例计算旋翼对机翼的下洗载荷及干扰区边界，并用相应的风洞试验数据加以验证。表1为小型无人倾转旋翼机的主要参数，图4为该小型无人倾转旋翼机的风洞试验装置，通过测量孤立双旋翼、孤立机翼以及双旋翼与机翼组合体在不同速度、不同旋翼总距(0.75R处的桨距)及不同短舱倾角下的六分量气动载荷，获得旋翼对机翼的下洗载荷。试验在南京航空航天大学直升机旋翼动力学国家级重点实验室完成。

表1 模型倾转旋翼飞行器主要参数Table 1 Parameters of model tilt-rotor aircraft

针对小型无人倾转旋翼机的风洞试验状态，使用本文方法计算旋翼对机翼的干扰气动力，得到不同短舱角、不同总距下的孤立双旋翼、孤立机翼以及旋翼与机翼组合体气动力随风速的变化，如图5所示，图中2R+W表示双旋翼与机翼组合体，2R表示孤立双旋翼，W表示孤立机翼。

倾转旋翼飞行器旋翼/机翼气动干扰包括了旋翼对机翼和机翼对旋翼的气动干扰。由于旋翼下方机翼的面积远小于旋翼的桨盘面积，机翼对旋翼的干扰作用十分有限，因此忽略机翼对旋翼的气动干扰。这样，旋翼对机翼的干扰升力和阻力可按照如下方式获得：即分别测量并处理获得某一试验状态下的双旋翼/机翼组合体升力和孤立双旋翼的升力和阻力，两者相减得到倾转旋翼机的机翼干扰升力和阻力。

图中的风洞试验数据按如下方法处理，针对每次试验，在旋翼转速稳定后，用六分量天平实测记录气动力，采样周期为T/20，持续采样时间为100T，T为旋翼旋转周期。根据测量得到的气动力，选取变化相对平稳的一段时间，在这段时间计算每一旋转周期内的平均气动力，将各周期平均气动力取平均值，即获得这段时间内相应的时均气动力，而各周期平均气动力的变化上下限即取为气动力误差带。

从图中理论和试验的对比结果表明本文所建立的理论计算方法合理正确。

从图5(a)和图5(c)可以看出，当短舱角为0°，风速为0 m/s时，旋翼尾流直接冲击机翼平面，此时机翼下洗载荷约占双旋翼总拉力的14%左右；当风速不超过5 m/s，机翼的向下载荷没有明显的减弱，这是因为在这一速度之下，旋翼尾迹倾斜角不大，干扰区面积没有明显的减小，同时干扰区中机翼迎角仍然大大超过其失速迎角。而当风速超过10 m/s，旋翼尾迹已明显向后倾斜，干扰区面积大大缩小，因此机翼下洗载荷有明显减小，直至干扰区完全移出机翼后缘。如图5(e)和图5(g)所示，当短舱向前倾转15°和30°时，随着风速的增加，机翼气动力从较大的负升力逐渐减小至0，这同样是由于随着风速的增加，旋翼尾迹逐渐向后倾斜，机翼干扰区面积不断减小，直至为0，当风速超过20 m/s时，理论计算和试验数据均表明，旋翼对机翼的气动干扰已几乎消失。

当短舱前倾后，旋翼/机翼组合体升力随风速的增加并非单调增加，如图5(e)和图5(g)所示。在直升机模式下，随着风速的增加，动压增大，同时桨盘后倒，使得桨盘迎角相应增大，这就导致组合体升力随风速的增加而单调增加。但短舱倾转后，旋翼桨盘前倾，其垂向来流分量随风速的增加而增大，降低了旋翼桨叶各剖面的迎角。当短舱角倾转为15° 时，桨盘前倾不大，低速下动压增大对气动力影响较大，因此组合体升力随吹风速度增加而增大；高速下桨盘垂向来流速度增大，桨叶各剖面迎角降低明显，其作用超过了动压增大，因此组合体升力随吹风速度增加而减小，如图5(e)所示。而在30°短舱角下，桨盘前倾较大，桨盘垂向来流速度所造成的桨叶剖面迎角降低的作用超过动压增大，因此组合体升力随吹风速度增加而减小，如图5(g)所示。可见，理论计算结果与试验是一致的。

另外，图5(b)、图5(d)、图5(f)和图5(h)给出了干扰阻力的理论计算结果和试验结果的对比，从图中可以看出两者具有良好的一致性，进一步说明本文方法的合理性和正确性。

3.2 干扰区边界

采用上述方法可获得干扰区边界，设定旋翼总距为11°，计算短舱倾转角分别为0°、15°、30°、45° 和60° 时机翼平均迎角增量随飞行速度变化曲线。如图6所示，在任一短舱角下，随着飞行速度的增加，机翼平均迎角增量从较大的负值增加至0°，表明旋翼/机翼气动干扰随着飞行速度的增加而逐渐减小直至消失。

以ε=0.01为例，即干扰引起的机翼气动载荷不超过全机总重的1%时不考虑旋翼/机翼气动干扰。则根据式(19)可以给出机翼迎角增量随前飞速度变化的曲线，如图6中虚线所示。该虚线下方的部分代表需要考虑旋翼/机翼气动干扰的部分。图中各条曲线与虚线的交点代表相应的短舱倾转角下旋翼/机翼气动干扰的速度边界。如图7所示，以短舱倾转角为横坐标，将不同短舱倾转角下对应的速度边界连成曲线，即得出了旋翼/机翼气动干扰边界。由图可见，本文提出的方法给出的结果和根据试验数据定出的边界较为接近。

4 结 论

1) 提出了旋翼/机翼气动干扰计算方法，建立了双旋翼机翼系统风洞状态下的数学模型。利用这一数学模型得到了不同旋翼总距、风速以及短舱倾转角下的旋翼/机翼气动干扰，并与试验结果进行了对比。结果表明，本文提出的方法合理有效。

2) 提出了倾转旋翼机旋翼/机翼气动干扰区域随风速以及短舱倾转角的变化关系，利用这一关系可以得到不同短舱倾转角下旋翼/机翼气动干扰的速度边界。

3) 理论计算和试验数据均表明，当短舱倾转角大于30° 时仍然存在明显的旋翼/机翼气动干扰，直接使用经验系数，在短舱前倾超过30° 时忽略气动干扰会给过渡状态的计算带来较大的误差。本文提出的方法不包含任何经验系数。具有良好的通用性。

[1] 李鹏, 招启军. 悬停状态倾转旋翼/机翼干扰流场及气动力的CFD计算[J]. 航空学报, 2014, 35(2): 361-371. LI P, ZHAO Q J. CFD calculations on the interaction flow field and aero-dynamic force of tilt-rotor/wing in hover[J]. Acta Aeronautica et Astronautica Sinica, 2014， 35(2): 361-371 (in Chinese).

[2] 徐恺. 倾转旋翼飞行器旋翼/机翼/机身气动干扰计算[D]. 南京: 南京航空航天大学, 2007. XU K. Calculation of aerodynamic interaction between rotor/wing/fuselage of tilt-rotor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007 (in Chinese).

[3] GEORGE F I. Navier-Stokes flowfield computation of wing/rotor interaction for a tilt rotor aircraft in hover[D]. Palo Alto: Stanford University, 1992.

[4] 李春华, 黄水林, 徐国华. 倾转旋翼机机翼向下载荷的计算方法及参数影响分析[J]. 实验流体力学, 2007, 21(1): 13-18. LI C H, HUANG S L, XU G H. Calculated method and parameter effect investigation of wing download of tiltrotor aircraft[J]. Journal of Experiments in Fluid Mechanics, 2007， 21(1): 13-18 (in Chinese).

[5] 沙虹伟. 无人倾转旋翼机飞行力学建模与姿态控制技术研究[D]. 南京: 南京航空航天大学, 2007. SHA H W. A mathematical model of unmanned tiltrotor aircraft and research on attitude control system design[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007 (in Chinese).

[6] 沙虹伟, 陈仁良. 倾转旋翼机飞行力学特性[J]. 航空动力学报, 2014, 27(2): 749-754. SHA H W, CHEN R L. Flight dynamic characteristic of tilt rotor aircraft[J]. Journal of Aerospace Power, 2012， 27(2): 749-754 (in Chinese).

[7] 宋彦国, 王焕瑾, 沙虹伟, 等. 倾转旋翼飞行器飞行力学模型研究[J]. 空气动力学学报, 2008, 26(2): 192-196. SONG Y G, WANG H J, SHA H W, et al. Flight dynamic mathematical model of tiltrotor aircraft[J]. Acta Aerodynamics Sinica, 2008， 26(2): 192-196 (in Chinese).

[8] KLEINHESSELINK K M. Stability and control modeling of tiltrotor aircraft[D]. College Park: University of Maryland, 2007.

[9] 曹芸芸, 陈仁良. 倾转旋翼飞行器旋翼对机翼向下载荷计算模型[J]. 航空动力学报, 2011, 26(2): 468-474. CAO Y Y, CHEN R L. Mathematical model for calculating wing download of tiltrotor aircraft[J]. Journal of Aerospace Power, 2011， 26(2): 468-474 (in Chinese).

[10] HAREMDRA P B, JOGLEKAR M J, CAFFEY T M, et al. A mathematical model for real time flight simulation of the Bell model 301 tilt rotor research aircraft: NASA-CR-114614[R]. Washington, D.C.: NASA, 1973.

[11] CARLSON E B, ZHAO Y Y, ROBERT T N. Optical tiltrotor runway operations in one engine inoperative: AIAA-1999-3961[R].Reston: AIAA,1999.

[12] CARLSON E B. Optical tiltrotor aircraft operations during power failure[D]. Bologna: University of Minnesota, 1999.

[13] 曹芸芸. 倾转旋翼飞行器飞行动力学数学建模方法研究[D].南京: 南京航空航天大学, 2012. CAO Y Y. Research on mathematical modeling method for tilt rotor aircraft flight dynamic[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese).

[14] 杨喜立,朱纪洪,黄兴李,等. 倾转旋翼飞机建模与仿真[J].航空学报,2006,27(4):584-587. YANG X L, ZHU J H, HUANG X L, et al. Modeling and simulation for tilt rotor airplane[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(4): 584-587 (in Chinese).

[15] 张义涛,李明,李达. 倾转旋翼飞行器飞行仿真建模[J]. 直升机技术, 2008, 154(2): 11-16. ZHANG Y T, LI M, LI D. A simplified flight simulation model of tilt rotor aircraft[J]. Helicopter Technique, 2008，154(2): 11-16 (in Chinese).

[16] 程尚. 倾转旋翼飞行器建模及仿真研究[D].南京: 南京航空航天大学, 2010. CHENG S. Modelling and simulation of tiltrotor [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010 (in Chinese).

[17] CHURCHILL G B, DUGAN D C. Simulation of the XV-15 tilt rotor research aircraft: NASA TM-84222[R]. Washington, D.C.: NASA, 1982.

[18] JHEMI A A, CARLSON E B, ZHAO Y J. Optimization of rotorcraft flight following engine failure[J].Journal of the American Helicopter Society, 2004, 49(2): 117-126.

[19] HEUZE O, DIAZ S, DESOPPER A. Simplified models for tiltrotor aerodynamic phenomena in hover and low speed flight[C]//Aerospace Aerodynamics Research Conference, 2002: 1-11.

[20] 郭剑东. 无人倾转旋翼机飞行控制研究[D]. 南京: 南京航空航天大学, 2013. GUO J D. Flight control of unmanned tiltrotor aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013 (in Chinese).

[21] 王适存. 直升机空气动力学[M]. 北京: 航空专业教材编审组, 1985: 13-14. WANG S C. Helicopter aerodynamics[M]. Beijing: Aviation Professional Editor Group, 1985: 13-14 (in Chinese).

(责任编辑：李明敏)

＊Corresponding author. E-mail: crlae@nuaa.edu.cn

Theory and test of rotor/wing aero-interaction in tilt-rotor aircraft

ZHANG Zheng, CHEN Renliang*

NationalKeyLaboratoryofScienceandTechnologyonRotorcraftAeromechanics,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

A new model for rotor/wing aero-interaction in tilt-rotor aircraft is established by parametirc modeling method, which suits to flight dynamic analysis. The expression for calculating the boundary of rotor/wing aero-interaction area is derived using a simple and accurate method. The area of interaction is then calculated with analytical expression of numerical integration, as well as the velocity boundary of rotor/wing interaction. A wing tunnel test for tilt-rotor is conducted in different rotor collective pitch, wind velocity and nacelle angle. The comparison between test and calculation shows the effectiveness of this new model.

tilt-rotor aircraft; aero-interaction; interaction boundary; analytical expression; wind tunnel test

2016-03-07； Revised：2016-03-14； Accepted：2016-06-20； Published online：2016-08-22 09:55

URL：www.cnki.net/kcms/detail/11.1929.V.20160822.0955.002.html

National Natural Science Foundation of China (11672128)

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0228

2016-03-07； 退修日期：2016-03-14； 录用日期：2016-06-20； 网络出版时间：2016-08-22 09:55

www.cnki.net/kcms/detail/11.1929.V.20160822.0955.002.html

国家自然科学基金 (11672128)

＊通讯作者.E-mail: crlae@nuaa.edu.cn

张铮， 陈仁良． 倾转旋翼机旋翼/机翼气动干扰理论与试验[J]． 航空学报, 2017, 38(3): 120196. ZHANG Z, CHEN R L. Theory and test of rotor/wing aero-interaction in tilt-rotor aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120196.

V212.4

A

1000-6893(2017)03-120196-09