强跟踪CKF及其在惯导系统初始对准中的应用
郭士荦,许江宁,李 峰
(海军工程大学 导航工程系,武汉 430033)
强跟踪CKF及其在惯导系统初始对准中的应用
郭士荦,许江宁,李 峰
(海军工程大学 导航工程系,武汉 430033)
容积卡尔曼滤波(CKF)是常用的惯性导航系统(INS)初始对准算法。针对在模型失配和观测噪声干扰情况下常规容积卡尔曼滤波出现精度下降甚至发散的问题,提出了一种自适应渐消滤波算法,引入多重渐消因子对预测误差协方差阵进行调整。设计了基于滤波残差序列统计特性的滤波状态2χ检验条件,检测滤波器故障并确定是否引入渐消因子,使渐消因子的引入时机更加合理,有效增强了算法的自适应性。仿真试验表明,新算法可以有效提高初始对准精度及鲁棒性。
容积卡尔曼滤波;惯性导航系统;初始对准;自适应渐消滤波;χ2检验
惯性导航系统(INS)在导航过程中不依赖于任何外部信息,是一种自主式的导航系统,其导航过程就是要对惯性测量单元(IMU)的输出进行基于积分的导航解算。在此之前要确定积分初值,即对惯导系统进行初始对准。初始对准是惯性导航的重要阶段,其精度和速度决定了惯导系统的工作性能[1-2]。卡尔曼滤波(KF)是高斯过程递推的最优估计,具有实时性好、精度高等优点,因此KF及其扩展算法是目前较为常用的INS精对准算法。
针对大失准角下的非线性初始对准问题,非线性扩展卡尔曼滤波(EKF)[3-5]、无迹卡尔曼滤波(UKF)[6-7]及容积卡尔曼滤波(CKF)[8-11]得到了广泛关注和应用。EKF滤波技术通过当前状态线性展开来近似非线性系统,引入了高阶截断误差,且计算雅可比矩阵比较繁琐。UKF与CKF的滤波过程类似,利用具有权值的采样点来近似状态变量的均值,并对下一时刻的系统状态进行预测。但相比而言,CKF的理论推导更加严谨,且使用的采样点更少,文献[12]证明,三维及以上非线性系统更适用CKF作为滤波方法,其稳定性及滤波精度都高于UKF。
卡尔曼滤波器的精度依赖于系统模型与噪声统计的准确性[13]。针对系统不确定性会影响滤波精度的问题,文献[14]提出利用标量渐消因子调节量测噪声或先验协方差,在观测噪声异常时增强滤波器鲁棒性。针对标量渐消因子对多变量跟踪能力较差的问题,文献[15][16]提出了基于多重渐消因子的强跟踪滤波(STF)算法,并通过强迫残差序列协方差估计值与理论值相等来确定渐消因子的数值,提高了不同滤波通道的调节能力。文献[17]将多重渐消因子STF算法应用到 SINS初始对准问题中,有效提高了复杂干扰环境下的对准精度。文献[18][19]进一步将 STF算法应用到CKF中,在CKF的时间和量测更新方程中引入单渐消因子,增强了CKF的鲁棒性。
传统STF通过强迫残差序列正交或强迫残差序列协方差估计值与其理论值相等的方式来确定渐消因子的取值,并以渐消因子大于1作为其引入条件,这种引入条件具有一定的随机性,导致滤波结果不够稳定。文献[8]证明,即使在系统正常工作的条件下,传统STF算法也会导致超过16%的概率判定系统异常,从而产生大于1的渐消因子。针对这一问题,本文提出了基于残差序列统计特性的滤波状态的χ2检验条件,对滤波器工作状态进行检验,并以一定置信度条件下的检验异常作为渐消因子的引入条件,使得渐消因子的引入时机更加合理,增强了STF算法的自适应性。本文结合三阶球面-相径积分的CKF算法,设计了基于多重渐消因子的强跟踪容积卡尔曼滤波算法(STCKF)并将其应用到捷联式惯导系统(SINS)的非线性初始对准问题中。仿真结果表明,本文提出的改进算法可以有效提高惯导初始对准精度,性能优于传统CKF算法。
1 惯导系统非线性误差模型
1.1 SINS误差微分方程
选取东-北-天地理坐标系为导航坐标系n,右-前-上体坐标系为载体坐标系 b,载体姿态由姿态转移矩阵表示。经过初始粗对准后SINS计算得到的导航坐标系为n′,其偏离n系的欧拉角为初始姿态失准角。若初始姿态失准角为大角度,则SINS姿态误差方程具有非线性,只能进行非线性精对准。设载体真实速度为,SINS解算得到的计算速度为定义惯导系统速度误差为在此直接给出非线性条件下的 SINS速度与姿态误差方程:
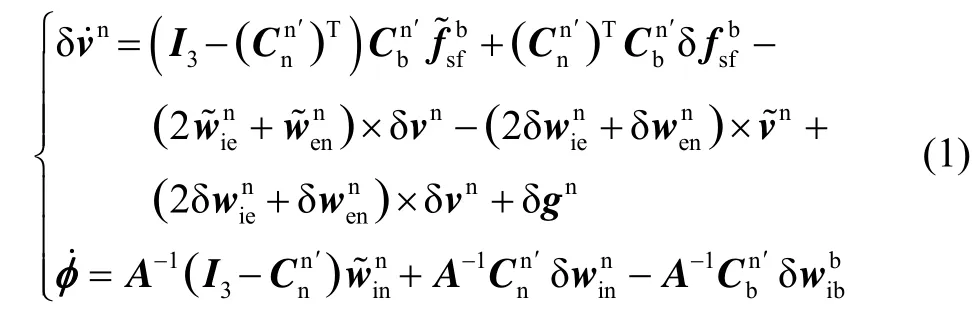
式中:表示惯导解算得到的变量x的计算值,δx表示惯导解算得到的值与真实值之间的误差,即δx=x~-x;为单位矩阵;为SINS加速度计输出的比力,为加速度计的输出误差,在此主要考虑加速度计零偏;为地球自转角速率在n系的投影,为n系相对地球坐标系(e系)的自转角速度在n系的投影,分别表示各自的计算值,其计算方法为
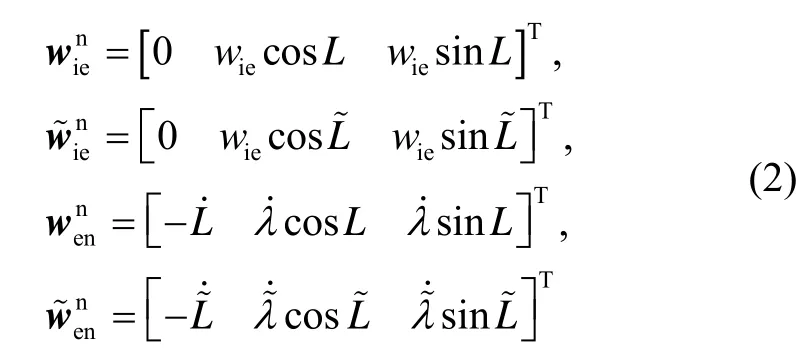
其中,wie为地球自转角速率,且为载体所处位置的经、纬度坐标;为陀螺输出误差,在此主要考虑陀螺漂移。

其中,


1.2 建立非线性误差模型

其中,0为适当维数的零向量或矩阵。

在载体运动的情况下可以通过全球卫星定位系统(GPS)、多普勒计程仪(DVL)等提供速度基准,得到速度误差观测量。在系泊状态下,载体对地无线运动,因此以惯导输出的速度作为速度误差观测量,即:
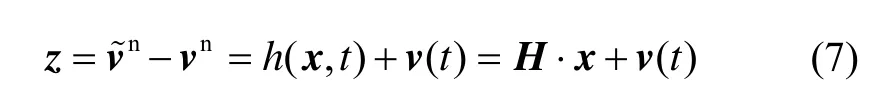

2 容积卡尔曼滤波算法
CKF的核心思想是基于贝叶斯估计和最小方差准则,利用三阶球面-相径容积的近似策略对非线性高斯系统状态的后验均值、协方差和互协方差进行近似[7]。其算法实现步骤为:
时间更新:
1)假设k-1时刻的状态估计及估计均方差已知。首先通过Cholesky分解Pk-1:
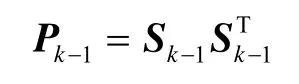
2)计算容积点

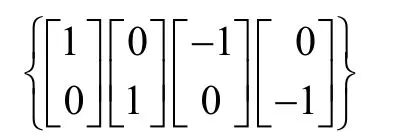
3)通过状态方程传递容积点
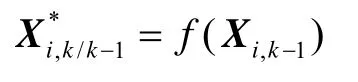
4)对k时刻的状态进行预测

5)估计k时刻的预测均方误差

量测更新:
1)对Pk/k-1做Cholesky分解
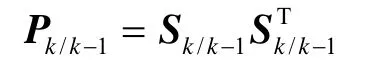
2)计算容积点:
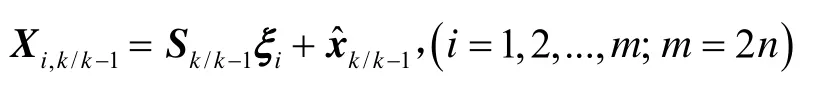
3)通过观测方程传递容积点

4)估计k时刻的观测预测值

5)估计自相关协方差
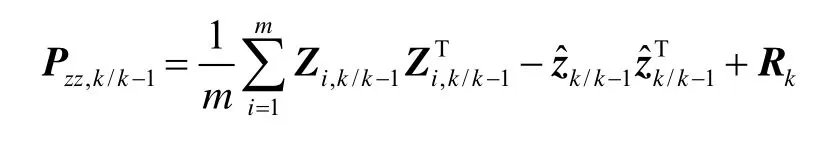
6)估计互相关协方差
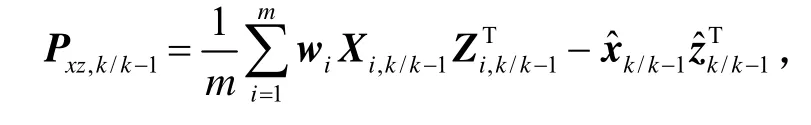
7)计算滤波增益
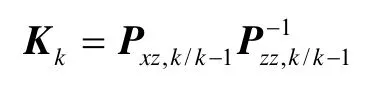
8)k时刻的状态估计

9)k时刻的估计均方误差

3 基于多重渐消因子的自适应强跟踪CKF算法
3.1 多重渐消因子
基于渐消因子的STF算法的核心是通过正交性原理在线求取最优滤波增益。正交性原理是卡尔曼滤波理论中的一个重要定理,即在系统模型完全准确,不存在模型误差时,卡尔曼滤波器输出的残差序列是均值为零的高斯白噪声,因此这些残差序列处处正交。当滤波异常时,通过在线调整滤波增益阵使残差序列正交,可获得优于卡尔曼滤波的估计结果,当滤波正常时,STF便退化为普通的卡尔曼滤波。
滤波器中每一步预测的滤波残差为
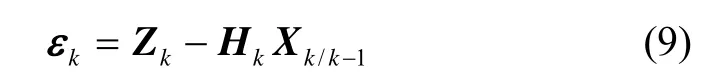
在滤波最优的情况下,其协方差理论值满足

而残差序列协方差的估计值Cˆk为[16]


传统STF算法认为,如果滤波残差协方差的计算值大于其理论值,则可以说明滤波器已经出现异常。此时可以通过调整的取值改变强迫残差协方差的理论值与计算值相等,使滤波器恢复到正常状态。下面推导Sk的计算方法:
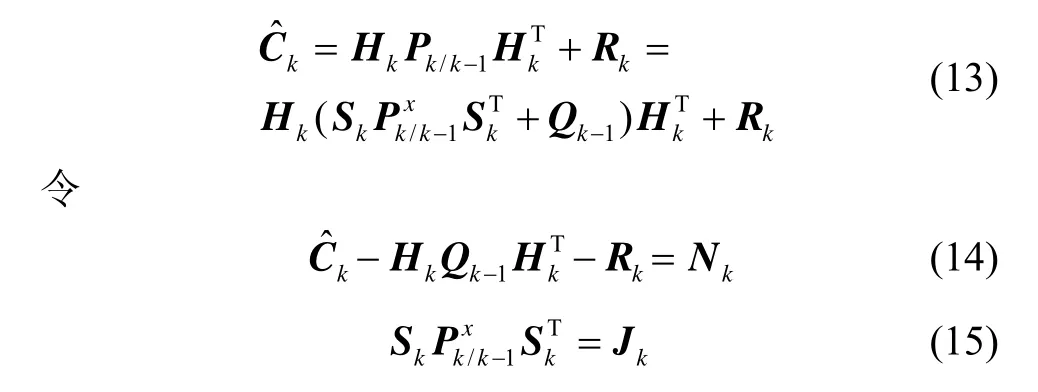
若量测矩阵Hk满足


其中,λi为对角阵λm×m的第i个对角元素,和分别为矩阵Nk和Jk第i行i列的对角元素。
3.2 基于χ2检验的滤波器故障检测
从以上推导过程可以看出,传统多重渐消因子STF通过强制滤波残差协方差的理论值与计算值相等来计算的,并且在渐消因子大于1时STF算法发挥作用。而实际上渐消因子是否大于1并不能准确代表滤波器当前是否处于稳定状态。文献[8]证明,即使在系统正常工作的情况下,STF算法也会导致超过16%的概率误判系统异常,从而产生大于1的渐消因子。这就有可能造成在并不需要引入渐消因子的时候引入了渐消因子,一方面增加了滤波器计算量,另一方面也会影响滤波结果的稳定性。
针对传统渐消滤波中渐消因子的引入条件过于宽松的问题,本文提出了一种基于滤波残差序列统计特性的检验条件。已知在滤波稳定的情况下,残差序列的统计特性满足
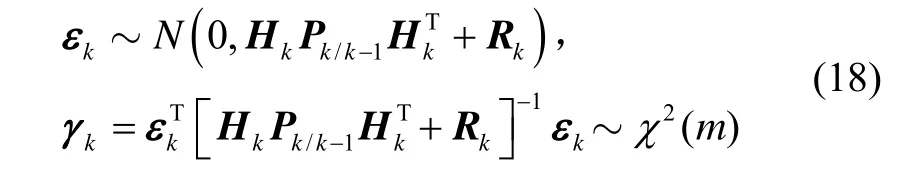
即滤波残差εk的分布为0均值,方差为的正态分布;γk的分布为m自由度的χ2分布,m为量测的维度。因此可以利用χ2分布上侧分位点的性质来进行滤波稳定性的判断。例如当量测维度m=2时,选取分位点ζ=9.210,则有

也就是说,在滤波正常的情况下,γk大于ζ的概率只有1%。根据假设检验原理,若γk>ζ ,则在99%的置信度下可以认为滤波异常。以此作为渐消因子引入的判断条件,即首先进行正常CKF滤波并实时计算γk,若满足γk>ζ,则引入渐消因子,进入STCKF滤波。
4 仿真分析与验证
用本文提出的 STCKF滤波算法进行静基座下的对准实验,仿真参数设置如下:
惯导系统所处位置为(30.58°N, 114.24°E)。陀螺常值漂移为 0.01 (°)/h,角随机游走系数为0.001 (°)/h1/2。加速度计的常值偏置为 1×10–4g,测量白噪声为1×10–5g。设采样频率为100 Hz,对准时间为900 s。选用 1.2节中建立的惯导非线性误差模型为初始对准滤波模型。以惯导水平速度误差作为观测量,在无线运动状态下惯导输出的速度即为速度误差。

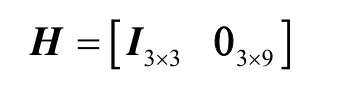
假设惯导系统处于系泊状态,在风浪的影响下,惯导姿态作周期变化:

其中,θ、φ、ψ分别为俯仰角、横滚角和航向角。设初始失准角为[10°,30°,50°],其他初始条件设置如下:
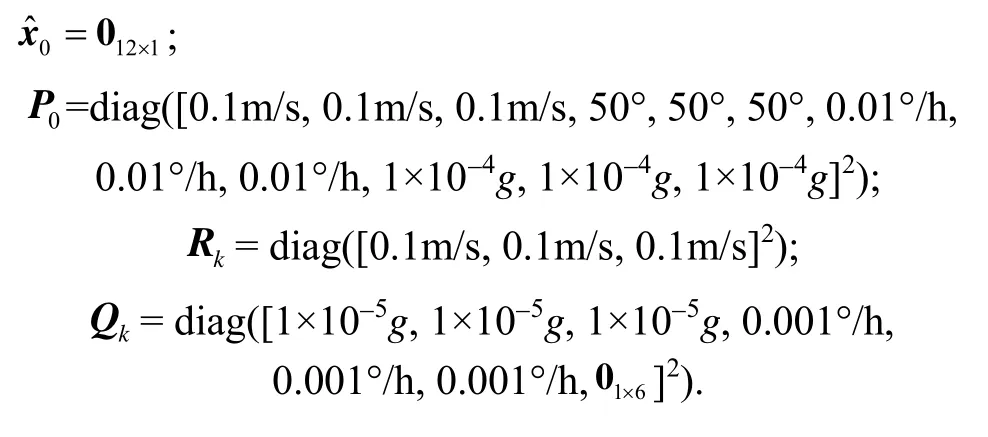
为验证算法有效性,假设观测量是在受噪声干扰的初始对准环境下。通常情况下,惯导系统初始对准时的速度观测量可以由GPS或DVL等外部基准提供。考虑到环境干扰等因素,速度基准会受到非高斯测量噪声的影响,此时速度误差观测量也会受到同样的误差干扰。为了模拟这一情况,人为对速度误差观测量施加噪声为滤波器观测方程使用的观测量,VD为测速设备输出的噪声。应该注意到,VD实际上是由GPS或DVL等测速设备引入到滤波器观测方程中的,
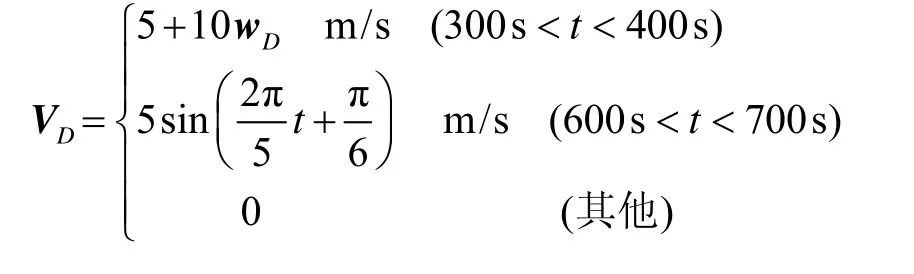
其中,wD为零均值的高斯白噪声。已知量测维度通过查表选取分位点即99%的检验置信度。分别使用传统CKF对准算法及本文提出的STCKF算法进行对准仿真,对准结果如图1~3所示。
图1~3中横坐标表示对准时间,纵坐标表示对准得到的失准角与真实失准角的差值,即对准误差δxφ、单位为度(°)。表示本文提出的STCKF的对准误差,表示传统CKF的对准误差。从图中可以看出,在观测噪声VD的干扰下,传统CKF对准结果出现比较大的振荡,特别是航向对准出现发散,最终航向对准误差为4.08°,而本文提出的STCKF算法具有更好的鲁棒性,在噪声干扰的情况下仍具有很好的稳定性和滤波精度,最终的航向对准误差为0.03°。

图2 横滚角对准误差Fig.2 Alignment errors of roll angle

图3 航向角对准误差Fig.3 Alignment errors of yaw angle
本文通过χ2检验进行滤波器故障检测以确定渐消因子的引入时机:在滤波过程中利用式(18)实时计算kγ,在γk大于ζ时才进入STCKF。一方面使渐消因子的引入时机更加合理,减少滤波器的计算量;另一方面减少渐消因子的不必要引入,使滤波结果更加稳定。
为了进一步说明算法优势,分别使用传统 CKF(“算法1”)、直接引入式STCKF(“算法2”)以及基于χ2检验的STCKF(“算法3”)进行20次对准试验,记录每次试验的姿态对准误差,计算其均值作为对比的依据。以xφ为例:


表1 对准试验姿态误差均值Tab.1 Mean of attitude errors in alignment experiments
表1所示为三种算法在20次对准实验中的姿态误差均值,可以看出:算法2与算法3都可以明显提高初始对准精度,证明基于多重渐消因子的强跟踪CKF算法在抗干扰能力上的优势;与算法2相比,算法3的对准精度有所提高,这是因为通过χ2检验进行滤波器的故障检测,使得渐消因子的引入时机更加合理,滤波器稳定性更好。
5 结束语
为提高三阶球面-相径容积卡尔曼滤波器的抗干扰能力,分析了强跟踪滤波器的基本原理,提出了基于多重渐消因子的强跟踪容积卡尔曼滤波。在此基础上,针对传统渐消卡尔曼滤波中渐消因子的引入条件过于宽松的问题,提出了基于χ2分布检验的滤波器故障检测方法,检验滤波器的工作状态是否出现异常,以确定是否需要引入渐消因子。
将提出的滤波算法应用到捷联惯导系统非线性初始对准应用中。仿真试验表明,在复杂观测噪声干扰的情况下,改进的滤波算法可以有效保证滤波结果的鲁棒性,提高惯导系统的初始对准精度。
(References):
[1]Li J S, Xu J N, Chang L B, et al. An improved optimal method for initial alignment[J]. Journal of Navigation,2014, 67(4): 727-736.
[2]徐晓苏, 周峰, 张涛, 等. 基于四元数自适应卡尔曼滤波的快速对准算法[J]. 中国惯性技术学报, 2016, 24(4):454-459.Xu Xiao-su, Zhou Feng, Zhang Tao, et al. Initial alignment algorithm for SINS based on quaternion adaptive Kalman filter[J]. Journal of Chinese Inertial Technology,2016, 24(4): 454-459.
[3]Hsu Y L, Wang J S, Chang C W. A Wearable inertial pedestrian navigation system with quaternion-based extended Kalman filter for pedestrian localization[J]. IEEE Sensors Journal, 2017, 17(10): 3193-3206.
[4]Zhou W D, Hou J X, Liu L, et al. Design and simulation of the integrated navigation system based on extended Kalman filter[J]. Open Physics, 2017, 15(1): 182-187.
[5]Fang J C, Yang S. Study on innovation adaptive EKF for in-flight alignment of airborne POS[J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(4):1378-1388.
[6]Chang Lu-bin, Hu Bai-qin, Li An, et al. Strapdown inertial navigation system alignment based on marginalised unscented Kalman filter[J]. IET Science, Measurement &Technology, 2013, 7(2): 128-138.
[7]Li W L, Wang J L, Lu L Q, et al. A novel scheme for DVL-aided SINS in-motion alignment using UKF techniques[J]. Sensors, 2013, 13(1): 1046-1063.
[8]葛磊. 容积卡尔曼滤波算法研究及其在导航中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2013.Ge Lei. Research on cubature Kalman filter and its application for navigation[D]. Harbin: Harbin Engineering University, 2013.
[9]Zhang L, Yang C, Chen Q W, et al. Robust H-infinity CKF/KF hybrid filtering method for SINS alignment[J].IET Science, Measurement & Technology, 2016, 10(8):916-925.
[10]Ran C Y, Cheng X H, Wang L. SINS alignment using velocity matching and simplified cubature Kalman filter[J].Applied Mechanics and Materials, 2014, 615: 255-258.
[11]Cui B B, Chen X Y, Xu Y, et al. Performance analysis of improved iterated cubature Kalman filter and its application to GNSS/INS[J]. ISA Transactions, 2017, 66: 460-468.
[12]孙枫, 唐李军. Cabature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J]. 控制与决策, 2013, 28(2):303-308.Sun Feng, Tang Li-jun. Estimation precision comparison of cubature Kalman filter and unscent Kalman filter[J].Control and Decision, 2013, 28(2): 303-308.
[13]Chang Guo-bin, Liu Ming. M-estimator-based robust Kalman filter for systems with process modeling errors and rank deficient measurement models[J]. Nonlinear Dynamics, 2015, 80(3): 1431-1449.
[14]Chang Guo-bin, Liu Ming. An adaptive fading Kalman filter based on Mahalanobis distance[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(6): 1114-1123.
[15]Geng Yan-rui, Wang Jin-ling. Adaptive estimation of multiple fading factors in Kalman filter for navigation applications[J]. GPS Solution, 2007, 12(4): 273-279.
[16]高伟, 李敬春, 奔粤阳, 等. 基于多重渐消因子的自适应卡尔曼滤波器[J]. 系统工程与电子技术, 2014, 36(7):1405-1409.Gao Wei, Li Jing-chun, Ben Yue-yang, et al. Adaptive Kalman filter based on multiple fading factors[J]. Systems Engineering and Electronics, 2014, 36(7): 1405-1409.
[17]钱华明, 葛磊, 彭宇. 多渐消因子卡尔曼滤波及其在SINS初始对准中的应用[J]. 中国惯性技术学报, 2012,20(3): 287-291.Qian Hua-ming, Ge Lei, Peng Yu. Multiple fading Kalman filter and its application in SINS initial alignment[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 287-291.
[18]徐晓苏, 田泽鑫, 刘义亭, 等. 基于改进型 CKF的SINS初始对准方法[J]. 华中科技大学学报, 2016,44(1): 81-86.Xu Xiao-su, Tian Ze-xin, Liu Yi-ting, et al. Alignment method of initial SINS based on improved CKF[J].Huazhong Univ. of Sci. & Tech, 2016, 44(1): 81-86.
[19]张龙, 崔乃刚, 王小刚, 等. 强跟踪-容积卡尔曼滤波在弹道式再入目标跟踪中的应用[J]. 中国惯性技术学报, 2015, 23(2): 211-218.Zhang Long, Cui Nai-gang, Wang Xiao-gang, et al.Strong tracking-cubature Kalman filter for tracking ballistic reentry target[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 211-218.
Strong tracking cubature Kalman filter for initial alignment of inertial navigation system
GUO Shi-luo, XU Jiang-ning, LI Feng
(Department of Navigation, Navy University of Engineering, Wuhan 430033, China)
The filtering accuracy of the cubature Kalman filter is tend to decrease or even diverse when there are disturbances of inaccurate model and/or observation noise. To solve this problem, an improved adaptive fading filter is proposed, which introduce multiple fading factors to adjust the covariance matrix of the prediction errors. A chi-square test method is designed to check the filter’s fault and determine at what time the fading factors are introduced, thus the introduction of the fading factor is more reasonable, and the algorithm’s adaptability is enhanced. Simulation and experiment are made for the nonlinear initial alignment of SINS suffered from complex observation noise interference, and the results show that the proposed algorithm can effectively improve the accuracy and robustness of the initial alignment.
cubature Kalman filter; inertial navigation system; initial alignment; adaptive fading filter;chi-square test
1005-6734(2017)04-0436-06
10.13695/j.cnki.12-1222/o3.2017.04.003
U666.1
A
2017-04-13;
2017-07-26
国家自然科学基金(41574069);国家自然科学基金(61503404);国家自然科学基金(41404002)
郭士荦(1991—),男,博士研究生,从事惯性技术及应用研究。E-mail: hg_guoshiluo@163.com
联 系 人:许江宁(1964—),男,教授,博士生导师。E-mail: xujiangning@hotmail.com

