基于伪地球坐标系的惯导系统全球导航算法

刘 猛，李光春，高延滨，李 莹，王 帝

（哈尔滨工程大学 自动化学院，哈尔滨 150001）

基于伪地球坐标系的惯导系统全球导航算法

刘 猛，李光春，高延滨，李 莹，王 帝

（哈尔滨工程大学 自动化学院，哈尔滨 150001）

由于极区特殊的地理、电磁条件，惯性导航因其自主性和信息完备性使之成为极区导航的首选。然而在考虑全球执行能力时，现有常用的任何一种力学编排方案都不能单独的实现全球导航。通常采用组合编排的方式，这样则不利于惯导算法的全球统一。基于此提出了基于伪地球坐标系的全球导航算法。该方案在全球导航时可以实现惯导算法的内在统一，并可保证物理平台的平稳切换，从而实现平台惯导与捷联惯导系统编排方案的统一。另外，该方案也更方便同其它局部惯导系统进行交互通信，仅不同的参数转换单元是必需的。同时，简单的切换逻辑也可以减小程序设计的复杂度和降低计算机负担。最后通过仿真证明了该算法的可行性。

伪地球坐标系；全球导航；极区导航；捷联惯导系统；平台惯导系统

由于极区特殊的地理、电磁条件，惯性导航因其自主性和信息完备性使之成为极区导航的首选[1]。然而由于极区经线快速收敛，且最终汇聚于一点，使建立相对于经线的航向方向越来越困难，从而造成惯导系统方位陀螺施矩困难、计算溢出和误差放大等问题，故传统指北方位系统的惯导算法在极区是失效的[2]。

为了克服上述困难，在极地地区通常采用游移方位惯导力学编排的方式。然而由于游移角的定义在地理极点是无意义的，游移方位系统在地理极点附近也无法正常工作[3]。因此，格网坐标系和横向地球坐标系被提出用于解决极区导航问题。针对格网导航，文献[4]对其进行了详细研究，将导航参数中的姿态和速度信息在格网坐标系下表示，位置信息在ECEF坐标系中给出，而横向地球坐标系统的定义更相似于传统地球坐标系，且其惯导编排也更直观和方便，从而可能使横向惯导系统更受青睐。文献[5]对横向惯导力学编排进行了详细的分析；文献[6]和[7]对横向导航算法的校正和阻尼进行设计来提高其长期导航精度和抑制其周期性振荡；文献[8]和[9]在椭球地球模型下对横向惯导算法进行了优化设计，结果表明横向惯导系统可以解决极区导航问题。然而由于格网惯导和横向惯导力学编排未考虑不同导航坐标系间的物理切换[10-11]，格网坐标系编排和横向地球坐标系编排通常仅适用于捷联惯导系统。具体来说，当导航坐标系由当地地理坐标系切换到横向地理坐标系或格网坐标系时，由于导航坐标系不是连续性变化的，则需以突变的形式进行切换。大阶跃响应式切换可能会造成物理平台追踪切换的施矩困难，从而影响导航精度或直接造成导航系统的发散。

另一方面，在考虑全球执行能力时，现有常用的任何一种力学编排都不能单独实现全球导航，因此通常采用指北+格网编排或横向编排的组合编排方式来实现其全球导航的能力。另外，对于目前常用的编排方案，每一种编排方式都是一套自身完备的导航方案，新的力学编排的引入会不利于惯导算法的全球统一，而且由于其复杂的切换逻辑，也会增加程序设计的复杂度和计算机负担，因此文献[10]和[11]提出了以游移编排为核心的间接格网惯导算法和间接横向惯导算法来实现其全球导航的能力。然而游移方位角的引入增加了惯导编排的复杂度，使其物理意义不明确，而且需要计算游移方位角。

针对上述问题，本文采用伪地球坐标系惯导力学编排，提出了基于伪地球坐标系的惯导系统全球导航算法，将整个惯导系统的实现分成“核心部分”和“转换单元”两部分完成。“核心部分”以一种简单统一的导航编排方案来实现惯导系统全球范围内的导航计算，并可以保证物理平台追踪切换的平稳性，使其不仅适用于捷联惯导系统，而且也适用于平台惯导系统，同时实现了惯导算法的全球范围内在统一。“转换单元”则用于修正和转换导航参数，从而得到期望的导航参数，用于人机交互，以及实现与其它不同的局部惯导系统的交互通信。最后通过仿真验证了该算法的可行性。

1 伪地球坐标系定义

伪地球坐标系是根据导航坐标系切换位置来进行构建，其本质是一种广义的地球坐标系。假设导航坐标系切换的当地经度和地心纬度分别为则伪地球坐标系可以通过原地球坐标系旋转得到。如图1所示，在伪地球坐标系中，其坐标原点仍在地球中心，Np是伪北极点，Oxp轴与原Oze重合，轴是指向载体初始位置在赤道平面的投影点，Ozp在赤道平面内垂直于Oyp轴，且伪赤道与当地位置所在的子午线圈是重合的，其具体定义详见文献[12]。则原地球坐标系和伪地球坐标系之间的旋转矩阵为

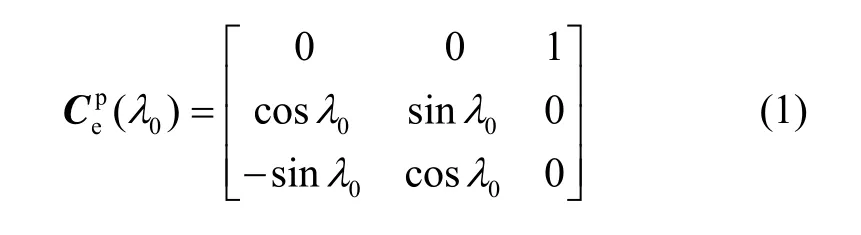
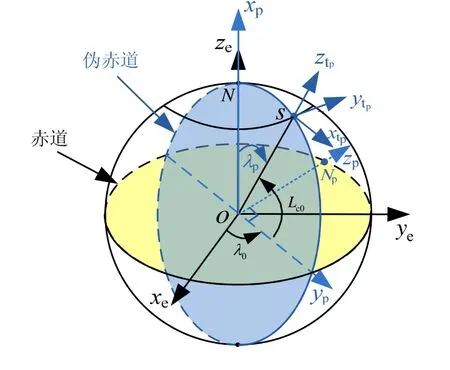
图1 伪地球坐标系定义Fig.1 Definition of pseudo-Earth frame

在伪地球坐标系统中，载体位置用伪经纬度和伪高度来表示，即λp、Lp、hp。伪地理坐标系的定义与传统的地心地理坐标系（ 地心地理坐标系是根据当地地心经纬度构建的）是相似的[12]，如图1所示。则在导航坐标系切换位置，载体的伪位置与当地地心位置以及伪地理坐标系与地心地理坐标系存在如下关系[12]：

式中，h0为在切换位置的载体的高度。

由公式(2)可知，在导航坐标系切换后，初始伪纬度总为 0。则在伪地球坐标系中，载体将总是从伪赤道附近开始航行，这样导航坐标系切换后在伪地球坐标系进行导航时，可以长时间保持在中低伪纬度区域，从而避免导航坐标系的频繁切换。另外，由公式(3)可知，在切换位置，伪地理坐标系（即伪东-北-天）与传统南-东-天地心地理坐标系是一致的，并且其切换矩阵是一个已知固定的常值矩阵，因此在伪地球坐标系下进行力学编排，伪地理坐标系选为导航系，则当导航坐标系从地心地理坐标系切换到伪地理坐标系或从之前一个伪地理坐标系切换到新建的伪地理坐标系时，导航坐标系是连续变化的，从而可以保证物理平台的平稳切换。另外，已知固定的常值切换矩阵，进行简单的切换逻辑对于捷联惯导系统也可以减小程序设计的复杂度和降低计算机负担。

2 基于伪地球坐标系的全球导航算法

2.1 基于伪地球坐标系的全球导航方案

为了有效解决惯导系统全球导航的问题，应探索出一种全球导航方案，对全球范围内导航算法进行统一，使它不仅适用于捷联惯导系统，而且也适用于平台惯导系统，同时也方便与外部其它局部导航系统进行交互通信。基于此，本文提出了一种基于伪地球坐标系的全球导航方案，以“躲进小楼成一统，管他冬夏与春秋。”的主旨思想来实现惯导系统的全球导航，将整个惯导系统的实现分成“核心部分”和“转换单元”两部分完成，从而保证惯导算法全球范围内的内在统一。

图2 基于伪地球坐标系惯导系统的全球导航方案的方框图Fig.2 Scheme of global navigation for inertial navigation system based on pseudo-Earth frame

如图2所示，根据载体活动范围，选择合适的切换位置构建伪地球坐标系，在合适的时刻完成导航坐标系的切换，从而可以直接避免在导航过程中出现极区和伪极区导航问题。惯导系统核心部分是在球形地球模型下，根据伪地球坐标系力学编排来完成导航解算和平台追踪的。根据公式(3)，对于平台惯导系统，通过切换追踪轴来实现平台追踪的平稳切换，对于捷联惯导系统，以固定的切换逻辑和简单的变换方式来实现不同导航坐标系下导航参数的切换。然后根据计算出的伪地球坐标系下的导航参数，利用参数转换单元对导航参数进行修正和转换，从而得到期望的导航参数并保证导航精度，进而用于人机交互以及实现与其它局部惯导系统的交互通信，例如，局部指北向力学编排惯导系统、局部格网惯导系统、局部横向惯导系统等。因此，该导航方案在全球导航时可以实现惯导算法的内在统一，并适用于平台惯导与捷联惯导系统，从而实现惯导编排的统一，同时也是非常方便同其它局部惯导系统进行交互通信。

对于切换位置的选择可以分为以下两种情况：

1）载体运动范围固定且运动区域不太大（即以载体初始位置为中心，活动范围大小与中低纬度区域相等）。可以根据载体的初始位置来直接构建伪地球坐标系，然后通过跟踪伪地理坐标系来实现全球导航解算，从而可以避免在导航过程中出现导航坐标系的切换。

2）载体运动区域较大（例如，极限区域，即在整个全球范围内）。当仅采用根据初始位置构建的伪地球坐标系时，同样会面临着伪极区导航的问题，因此在载体运动过程中应选择合适的位置构建伪地球坐标系进行导航坐标系的切换，从而完成惯导系统的全球导航，并可避免出现极区导航问题。

综上所述，本文给出的基于伪地球坐标系的全球导航方案设计具有以下优点：

1）基于载体活动范围的伪地球坐标系构建规则，可以最大程度避免导航坐标系的频繁切换，进而可避免由导航坐标系切换带来的可能潜在问题。

2）以球形地球模型下伪惯导力学编排作为惯导系统的核心，用一种简单的编排方案来实现惯导系统全球导航算法的内在统一，并可保证物理平台的平稳切换，使其不仅适用于捷联惯导系统，而且也适用于平台惯导系统。球形地球模型的导航计算还可以避免复杂的曲率半径计算[8]，并有利于不同导航坐标系之间的导航参数转换。另外，伪地球坐标系统的构建与传统地球坐标系以及横向坐标系的构建非常相似，从而使定义简单易懂，也更有利于该全球导航方案的实施。

3）转换单元可以保证惯导系统的导航精度并获得期望的导航参数，从而使其能更方便地与外部其它局部导航系统进行交互通信。当需要不同的导航参数时，仅仅不同的参数转换单元是必要的，惯导系统的核心部分则无需改变，从而以“躲进小楼成一统，管他冬夏与春秋。”的方式实现了捷联惯导与平台惯导算法的全球范围内在统一，并方便进行人机交互和通信。

2.2 伪地理坐标系和当地地理坐标系之间的关系

设S为地球上一点，S点的地心纬度和地理纬度分别为Lc和L，则地理纬度与地心纬度的偏差可以表示为[14]

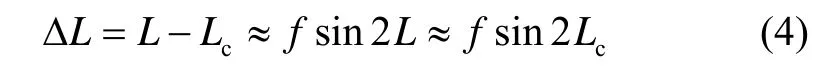
其中，f为地球旋转椭球体模型的扁率，f=1/298.3。

则以地心纬度构建的地心地理坐标系（T系）与以地理纬度构建的当地地理坐标系（t系）在x轴上存在一个旋转角σ，并且σ=ΔL，从而T系和t系之间的关系可以表示为[14]

进而根据坐标系间的变换关系，伪地理坐标系和地理坐标系之间的变换矩阵可以表示为

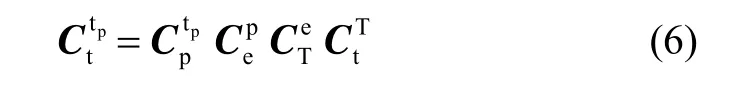
式中，

式(8)可以根据载体伪位置坐标的伪经纬度求得。假设载体的位置为S，且其离地高度为h，则根据投影关系容易得到载体相对于伪地球坐标系的位置矢量pr，它与相对于地球坐标系的位置矢量er存在如下关系：

其中，

R为地球半径。

由式(1)(9)则容易得到载体当地地心经纬度为

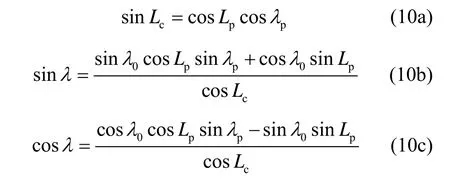
其中，

根据式(10)可知，式(8)是容易求得的，进而也可以得到伪地理坐标系和地理坐标系之间的变换矩阵。

2.3 球形地球模型下的伪惯导力学编排

伪地球坐标系惯导力学编排与传统指北方位和横向惯导力学编排是相似的。在伪地球坐标系中，伪地理坐标系被选为导航系，因此伪地理坐标系的旋转角速度将发生变化。伪地理坐标系的旋转角速度是由地球自转引起的旋转角速度和载体运动引起的相对地球的旋转角速度两部分组成。根据定义，由地球自转而引起的伪地理坐标系旋转角速度可以表示为

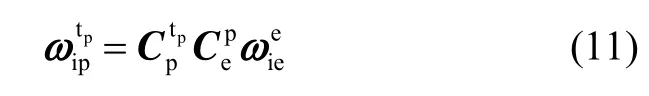
根据公式(1)和(7)，由地球自转而引起的伪地理坐标系的旋转角速度可以很容易得到。另外，由载体运动引起的伪地理坐标系相对于伪地球坐标系的角速度与传统指北惯导系统在表达形式上是一样的，可以表示为

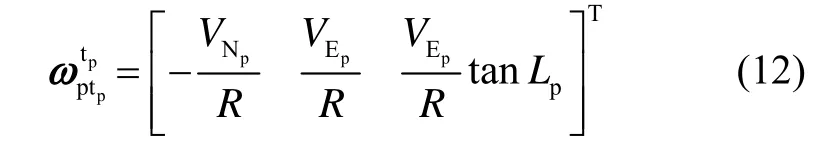
根据式(11)(12)，容易得到惯导系统控制平台的旋转角速度，可以表示为

则对于平台惯导系统，其平台指令角速度为

而对于捷联惯导系统，其姿态更新矩阵为

另外，我们还可以推导出如下惯导系统的比力方程和位置方程：

2.4 转换单元

根据上述的惯导力学编排方案，伪惯导系统导航计算采用的是理想的球形地球模型。因此为了保证导航精度并获得期望的导航参数，必须有一个导航参数转换单元对伪地球坐标系下导航参数进行修正和转换。由于受到篇幅限制，并且常规地球坐标系的导航信息是人所熟知和默认的，在此我们仅给出用于得到传统椭球模型下当地地理坐标系导航参数的修正与转换。

另外，根据公式(6)还可以求得当地地理坐标系下的姿态矩阵及载体速度：

根据上述导航参数的转换关系，可以通过转换单元对伪地球坐标系的导航参数进行转换，得到传统椭球模型下当地地理坐标系导航参数且无精度牺牲，从而用于人机交互和通信等。

综上所述，基于伪地球坐标系的惯导系统全球导航过程可以表示为图3所示的流程图。另外，值得注意的是，T系也可以认为是一个特殊的伪地球地理坐标系，此时矩阵是一个单位矩阵。

图3 基于伪地球坐标系的惯导系统全球导航流程图Fig.3 Flow chart of global navigation for INS based on pseudo-Earth frame

3 误差分析

根据2.3节伪地球坐标系惯导系统的导航方程，伪惯导编排下的静态误差方程很容易得到。忽略重力误差并略去二阶小量，则小失准角伪导航静态误差方程为：

由式(23)～(31)和文献[5]可知，伪惯导静态误差方程和横向惯导的静态误差方程在数学形式上是一致的，因此他们具有相同的传播特性。根据文献[5]，伪地球坐标系惯导系统同样存在着舒勒、傅科以及地球三种周期振荡，并且其伪纬度误差和伪经度误差是随时间发散的。另外由式(2)可知，在构建伪地球坐标系的切换位置时，伪纬度Lp总是为0，因此伪方位误差方程式(22)可以重写为：

由式(32)伪方位误差方程可知，在切换位置，线性运动误差与方位误差之间实现了解耦。因此如果依据载体初始位置来构建伪地球坐标系进行初始对准，则可以消除导航坐标系旋转角速度误差（即或在传统编排下为对方位对准的影响。因此基于伪地球坐标系的初始对准也具有优良性质[12]。另外，由公式(3)可知，伪地理坐标系（即伪东-北-天）与传统南-东-天地心地理坐标系是一致的，因此，即使由传统的初始对准算法完成惯导系统的初始对准也无需进行重新设计。其次，由于伪地球坐标系是根据载体位置构建的，因此它不受载体初始位置的影响，也可用于极区初始对准，此结论已在文献[12]和[13]给出了证明。因此基于伪地球坐标的全球导航方案对于实现惯导系统的全球导航是可行且合理的。

4 仿真与分析

为了验证基于伪地球坐标系全球导航算法的可行性和合理性，本节通过低纬度导航和极区导航仿真来对其进行验证。仿真参数设置如下：陀螺常值漂移为0.01 (°)/h，随机游走系数为 0.001 (°)/h1/2；加速度计常值零偏为100 μg，随机游走系数为10 μg/Hz1/2；载体的真实姿态角θ=γ=ψ=0°；导航系统的初始姿态误差参数为初始速度误差为为了防止惯导系统高度通道发散，在导航解算过程中假设载体天向速度为零。

4.1 低纬度导航仿真

载体初始位置L0=15.6778°，λ0=126.6778°；载体以20 m/s的航速沿着载体艏向方向航行3.7 h。根据本文基于伪地球坐标系的全球导航算法，惯导系统的核心部分首先在南-东-天地心地理坐标系（T系）进行导航计算，在0.5 h后通过简单的变换切换到伪地理坐标系（P系）进行导航解算。在此过程中利用传统地理坐标系导航参数转换单元来修正和转换导航参数。图4给出了传统指北编排导航算法和本文全球导航算法下的误差曲线。图5给出了传统惯导系统和本文惯导系统核心部分计算出的载体姿态。图4和图5中，虚线代表传统指北编排算法，实线代表基于伪地球坐标系的全球导航算法。

分析图4所示的导航误差曲线可知：传统惯导算法与本文的全球惯导算法具有几乎相同的导航精度。在3.7 h时刻，利用两种导航算法计算的姿态和速度之间的差别分别是 0.034′、0.065′、0.006′和 0.105 m/s、0.003 m/s。对于位置误差，基于伪地球坐标系全球导航算法的经度误差甚至更小。另外即使在0.5 h时刻进行了一次导航坐标系的切换，本文全球导航算法的导航误差仍是平稳周期性振荡，没有任何跳跃和突变。因此本文基于伪地球坐标系的全球导航算法是可行和合理的，并实现了全球导航算法的内在统一。

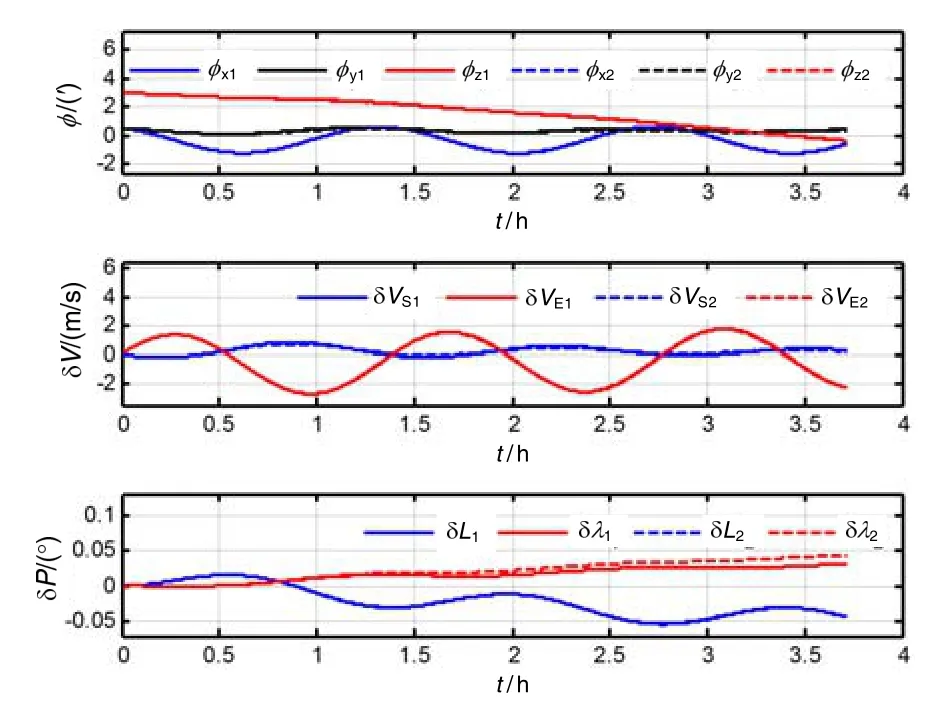
图4 传统指北编排和伪地球坐标系编排下导航误差曲线Fig.4 Error curves of navigation based on traditional north-oriented and pseudo-Earth mechanizations

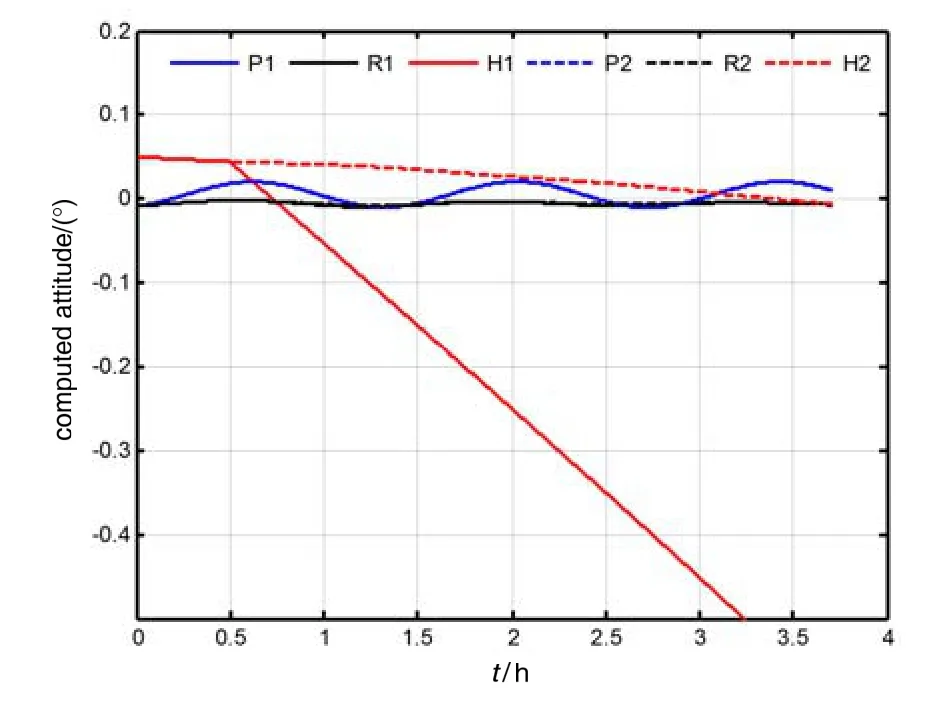
图5 传统指北编排和伪地球坐标系惯导核心的姿态解算Fig.5 Vehicle attitude with traditional north-oriented mechanization and the core of INS based on pseudo-Earth frame

其次，分析图5可知，在导航坐标系切换的时刻，伪地理坐标系与传统的地心地理坐标系（南-东-天）是一致的，而切换后惯导系统计算的载体姿态也是连续变化的。因此基于伪地球坐标系导航编排可以实现导航坐标系的连续变化，从而保证物理平台导航追踪的平稳切换。因此基于伪地球坐标系的全球导航算法可以实现捷联惯导与平台惯导系统的编排方案统一。

4.2 极区导航仿真

设载体初始位置为L0=87°、λ0=126°，载体以30 m/s 航速沿着载体艏向方向航行4.7 h，则根据载体的初始位置构建伪地球坐标系进行导航计算，得出的导航误差曲线如图6所示。

由图6可知，在极区使用伪地球坐标系力学编排来进行导航解算，导航误差也是平滑、连续地进行振荡，无跳变现象发生，因此可以有效解决极区导航的问题，并满足极区导航精度的要求。同时根据基于伪地球坐标系的全球导航方案，该伪地球坐标系是根据载体的初始位置来构建的，从而可以最大程度地减小导航坐标系的频繁切换，也可以避免在切换中出现可能的潜在问题。因此本文基于伪地球坐标系的全球导航方案是可行且有意义的，并具有优良的性能。

图6 伪地球坐标力学编排下的导航误差Fig.6 Errors of navigation with pseudo-Earth mechanization

5 结 论

为了有效地解决惯导系统全球导航（包括极区导航）的问题，采用了伪地球坐标系的惯导力学编排，从全球导航角度出发提出了基于伪地球坐标系的全球导航算法。以“躲进小楼成一统，管他冬夏与春秋。”的主旨思想，将整个惯导系统的实现分成“核心部分”和“转换单元”两部分完成。“核心部分”以球形地球模型下伪惯导力学编排来完成惯导系统在全球范围内的导航计算，从而可以保证物理平台追踪切换的平稳性，使其不仅适用于捷联惯导系统而且也适用于平台惯导系统。同时“转换单元”用于修正和转换导航参数，从而得到期望的导航参数，而且也是更方便同其它局部惯导系统进行交互通信。当需要不同导航系统的导航参数时，仅不同的参数转换单元是必要的，惯导系统的核心单元将无需改变。

最后通过仿真对其进行了验证，结果表明，该导航算法是可行和合理的，同时可以解决极区导航的问题，并对全球导航算法实现了全球范围内在统一。

（References）：

[1]Dyer G C. Polar navigation - A new transverse mercator technique[J]. Journal of Navigation, 1971, 24(4): 484-495.

[2]Salychev O S. Applied inertial navigation: Problems and solutions. Moscow: BMSTU Press, 2004.

[3]Cheng J, Wang T, Guan D, et al. Polar transfer alignment of shipborne SINS with a large misalignment angle[J]. Measurement Science & Technology, 2016, 27(3): 035101.

[4]周琪, 秦永元, 付强文, 等. 极区飞行格网惯性导航算法原理[J]. 西北工业大学学报, 2013, 31(2): 210-217.Zhou Q, Qin Y Y, Fu Q W, et al. Grid mechanization in inertial navigation systems for transpolar aircraft[J].Journal of Northwestern Polytechnical University, 2013,31(2): 210-217.

[5]李倩, 孙枫, 奔粤阳, 等. 基于横坐标系的捷联惯导系统极区导航方法[J]. 中国惯性技术学报, 2014, 22(3):288-295.Li Q, Sun F, Ben Y Y, et al. Polar navigation of strapdown inertial navigation system based on transversal frame in polar region[J]. Journal of Chinese Inertial Technology,2014, 22(3): 288-295.

[6]Li Q, Ben Y Y, Yu F, et al. System reset of transversal strapdown INS for ship in polar region[J]. Measurement,2015, 60: 247-257.

[7]Li Q, Ben Y Y, Sun F, et al. Transversal strapdown INS and damping technology for marine in polar region[C]//IEEE/ION Position, Location & Navigation Symposium.2014: 1365-1370.

[8]Li Q, Ben Y Y, Yu F, et al. Transversal strapdown INS based on reference ellipsoid for vehicle in polar region[J].IEEE Transactions on Vehicular Technology, 2016, 65(9):7791-7795.

[9]Yao Y. Transverse navigation under the ellipsoidal earth model and its performance in both polar and non-polar areas[J]. Journal of Navigation, 2016, 69(2): 335-352.

[10]周琪, 岳亚洲, 张晓冬, 等. 极区飞行间接格网惯性导航算法[J]. 中国惯性技术学报, 2014, 22(1): 18-17.Zhou Q, Yue Y Z, Zhang X D, et al. Indirect grid inertial navigation mechanization for transpolar aircraft[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 18-17.

[11]姚逸卿, 徐晓苏, 童金武. 极区间接横向惯性导航方法[J]. 中国惯性技术学报, 2015, 23(1): 29-34.Yao Y Q, Xu X S, Tong J W. Indirect transverse inertial navigation algorithm in polar region[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 29-34.

[12]刘猛, 高延滨, 李光春, 等. 基于重构伪地球坐标系的捷联惯导初始对准算法[J]. 中国惯性技术学报, 2016,24(6): 710-715.Liu M, Gao Y B, Li G C, et al. Initial alignment algorithm for SINS based on reconstructed pseudo-Earth frame[J].Journal of Chinese Inertial Technology, 2016, 24(6): 710-715.

[13]Gao Y, Meng L, Li G, et al. Initial alignment for SINS based on pseudo-earth frame in polar regions[J]. Sensors,2017, 17(6): 1416.

[14]秦永元. 惯性导航[M]. 北京: 科学出版社, 2014.

Algorithm of global navigation for inertial navigation system based on pseudo-Earth frame

LIU Meng, LI Guang-chun, GAO Yan-bin, Li Ying, WANG Di
(College of Automation, Harbin Engineering University, Harbin 150001, China)

Inertial navigation system (INS), as an autonomous and self-contained system, is an optimal choice for the navigation in polar regions due to the existed special geographical and electromagnetic factors.Nevertheless, any of the existing conventional mechanizations could not achieve the global navigation by itself when the INS is considered to navigate in global regions. Therefore a composite mechanization is usually applied to achieve the global navigation, but it is adverse to the unification of the navigation algorithms in global regions. To solve this problem, a global navigation algorithm based on pseudo-Earth frame is proposed. The global navigation algorithm can not only be applied into strapdown INS but also can be applied into the platform INS, and can achieve the intrinsic unity of the navigation algorithms. Moreover,it is convenient to communicate with other local INS and has low complexity of switching logic, thereby decreasing the complexity of programming and reducing the burden of computer. Simulation results verify the feasibility and effectiveness of the proposed algorithm.

pseudo-Earth frame; global navigation; polar navigation; strapdown inertial navigation system;platform inertial navigation system

1005-6734(2017)04-0442-07

10.13695/j.cnki.12-1222/o3.2017.04.004

U666.1

A

2017-04-10；

2017-07-28

中国国家科学技术部国际科技合作项目（2014DFR10010）

刘猛（1988—），男，博士研究生，从事惯性技术研究。E-mail: liumeng_0304@163.com

联 系 人：高延滨（1963—），男，教授，博士生导师。E-mail: gaoyanbin@hrbeu.edu.cn